An Overview of Nonparametric Bayesian Models and Applications

An Overview of Nonparametric Bayesian Models and Applications to Natural Language Processing Narges Sharif-Razavian and Andreas Zollmann

Motivation • Given: x 1, …, xn y 1, …, yn {p(x, y; θ)}θ • Find most appropriate θ • MLE: choose arg maxθ p(x 1, y 1; θ) … p(x. N , y. N; θ ) • Drawback: only events encountered during training acknowledged -> overfitting

Bayesian Methods Treat θ as random assign prior distribution p(θ) to θ use posterior distribution p(θ|D)=p(D|θ)p(θ)/p(D) ∝p(D|θ)p(θ) Compute predictive prob’s for new data points by marginalizing over θ: p(yn+1|y 1, …, yn)=∫θ p(θ|y 1, …, yn) p(yn+1|θ)

Dirichlet Priors • Let y 1, …, yn be drawn from Multinomial(β 1, …, βK) K outcomes, p(K; β)=βK • Conjugate prior: Dirichlet(α 1, . . . , αK ) distribution (where all αi > 0) : p(β; α 1, . . . , αK ) = β 1^(α 1 -1)…βK^(αK-1) • Predictive prob’s: p(y=k| y 1, …, yn)=

Dirichlet Process Priors • Number of parameters K unknown – Higher value for K still works – K could be inherently infinite • Nonparametric extension of Dirichlet distribution: Dirichlet Process • Example: Word segmentation – infinite word types

Dirichlet Process • Given a distribution H over event space Θ G ~ DP(α, H) • Predictive probability of θn+1 conditioned on the previous draws θ 1, . . , θn is

DP Model for Unsupervised Word Segmentation • Word types as mixture components • Unigram Model : • Infinite word types: Pw ~ DP(α, P 0) • Where • Posterior

HDP Model for Unsupervised Word Segmentation • Bigram Model: • The HDP Prior • The posterior

DP and HDP Model Results • CHILDES corpus – 9790 sentence – Baselines • NGS: Maximum Likelihood • MBDP: Bayesian unigram

Pitman-Yor Processes • Adds a discount parameter d to DP (α, H) more control over increase rate in the number of components as function of sample size • Prob. of value coming from H decreases according to (α+d*t)/(α+n) • t: n. o. draws from H so far • N. o. unique values = O(α n^d) [d>0] O(α log(n)) [d=0]

Language Modeling based on Hierarchical Pitman-Yor Processes • language modeling: assign a probability distribution over possible utterances in a certain language and domain Tricky: choice of n Smoothing (back-off or interpolation)

Teh, Yee Whye. 2006. A hierarchical Bayesian language model based on Pitman-Yor processes. (COLING/ACL). • Nonparametric Bayesian approach: ngram models drawn from distributions whose priors are based on (n-1)-gram models

Model Definition • u=u 1…um: LM context • Gu(w): prob of word w given u • dm ~ Uniform(0, 1) • θm ~ Gamma(1, 1) • Base cases:

Relation to smoothing methods • Paper shows that interpolated Kneser-Ney can be interpreted as approximation of HPY

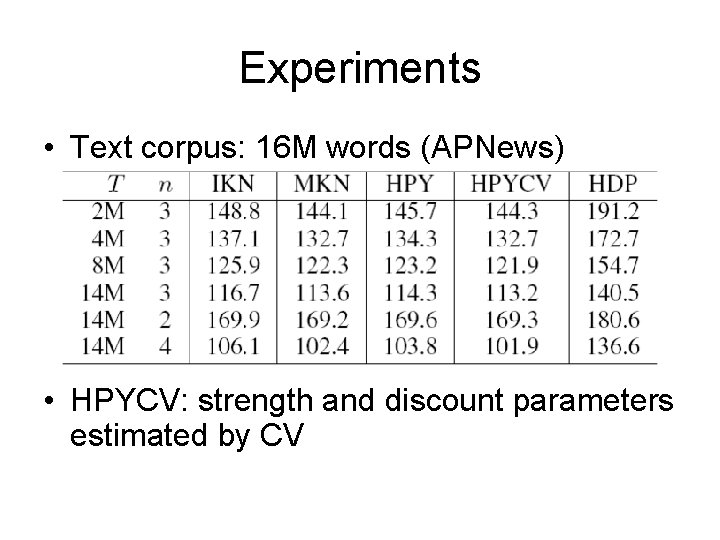
Experiments • Text corpus: 16 M words (APNews) • HPYCV: strength and discount parameters estimated by CV

Conclusions • gave an overview of several common nonparametric Bayesian models • reviewed some recent NLP applications of these models • use of Bayesian priors masters trade-off between – powerful model to capture detail in the data – having enough evidence in the data to support the model’s inferred parameters • computationally expensive and non-exact inference algorithms • none of the applications we reviewed improved significantly over a smoothed non-Bayesian version of the same model • nonparametric Bayesian methods in ML / NLP still in its infancy • need more insight into inference algorithms • new DP variants and generalizations being found every year.