An Overview of Echo Planar Imaging EPI Douglas

An Overview of Echo Planar Imaging (EPI) Douglas C. Noll, Ph. D. Depts. of Biomedical Engineering and Radiology University of Michigan, Ann Arbor Noll

Acknowledgements • • • Scott Peltier, Alberto Vazquez University of Michigan Drs. S. Lalith Talagala and Fernando Boada (University of Pittsburgh) • SMRT and ISMRM Noll

Objectives • Explain how EPI images are acquired and created • Describe hardware requirements • Describe EPI variants, terminology, and parameters • Demonstrate common EPI artifacts • Summarize applications of EPI Noll

Outline • • Pulse sequence basics Localization Variants on EPI Parameters EPI Artifacts EPI Hardware Applications Noll

Pulse Sequences • Two Major Aspects – Contrast (Spin Preparation) What kind of contrast does the image have? What is the TR, TE, Flip Angle, Venc? – Localization (Image Acquisition) How is the image acquired? How is “k-space” sampled? Noll

Pulse Sequences • Spin Preparation (contrast) – – – Spin Echo (T 1, T 2, Density) Gradient Echo Inversion Recovery Diffusion Velocity Encoding • Image Acquisition Method (localization, k-space sampling) – – – Spin-warp EPI RARE, FSE, etc. Noll

Localization vs. Contrast • In many cases, the localization method and the contrast weighting are independent. – For example, the spin-warp method can be used for T 1, T 2, or nearly any other kind of contrast. – T 2 -weighted images can be acquired with spinwarp, EPI and RARE pulse sequences. Noll

Localization vs. Contrast • But, some localization methods are better than others at some kinds of contrast. – For example, RARE (FSE) is not very good at generating short-TR, T 1 -weighted images. • In general, however, we can think about localization methods and contrast separately. Noll

Imaging Basics • EPI is an image localization method. – Two-dimensional localization. • To understand EPI, we will start at the beginning with one-dimensional localization. – Here we “image” in 1 D - the x-direction. (e. g. the L-R direction) • We start with the simplest form of localization called “frequency encoding. ” Noll

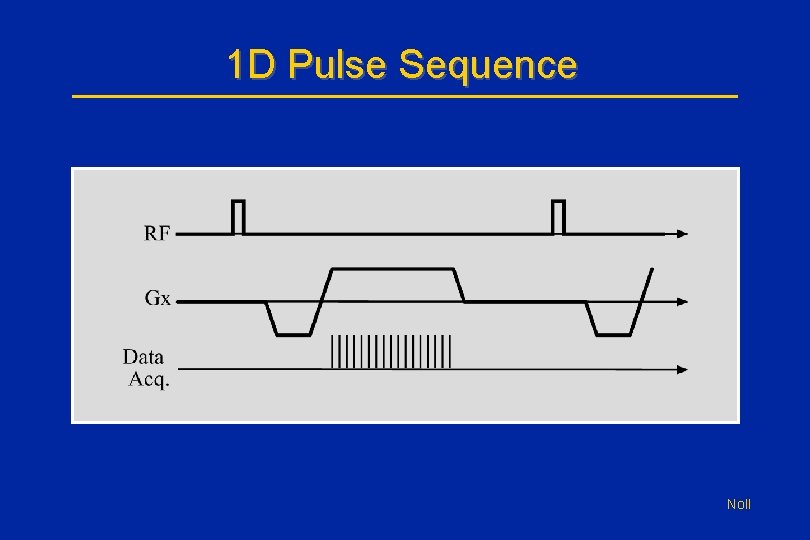
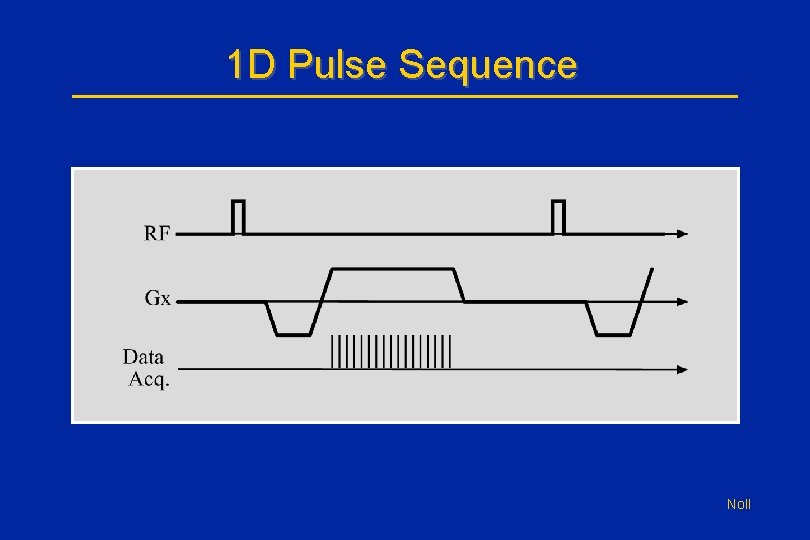
1 D Pulse Sequence Noll

1 D Localization • We acquire data while the x-gradient (Gx) is turned on and has a constant strength. • Recall that a gradient makes the magnetic field vary in a particular direction. • In this case, having a positive x-gradient implies that the farther we move along in the x -direction (e. g. the farther right we move) the magnetic field will increase. Noll

1 D Pulse Sequence Noll

Frequency Encoding • A fundamental property of nuclear spins says that the frequency at which they precess (or emit signals) is proportional to the magnetic field strength: f = g. B - The Larmor Relationship • This says that precession frequency now increases as we move along the x-direction (e. g. as we move rightwards). Noll

Frequency Encoding Noll

Fourier Transforms • The last part of this story is the Fourier transform. • The Fourier transform is the computer program that breaks down each MR signal into its frequency components. • If we plot the strength of each frequency, it will form a representation (or image) of the object in one-dimension. Noll

Fourier Transforms Noll

Alternate Method for 1 D Localization • In the case just described, the “frequency encoding” gradient was constant. – At different locations spins precessed at different frequencies. – This was true as long as the gradient was “on. ” • We now look at an alternate situation where the gradient is turned “on” and “off” rapidly. – At different locations spins will precess at different frequencies, but only during the times that the gradient is “on. ” Noll

Alternate Method for 1 D Localization Noll

On/Off Gradients in 1 D Localization • In the case previously described, the spins precessed smoothly. • In this case, the spins precess in a “stopaction” or jerky motion. • What is different here is that we sample the MR signal while it has stopped precessing. – At each step, the spatial information has been encoded into the phase. – This is a form of “phase encoding. ” Noll

Stop-Action Movement of Magnetization Sample 1 Sample 2 Sample 3 Noll

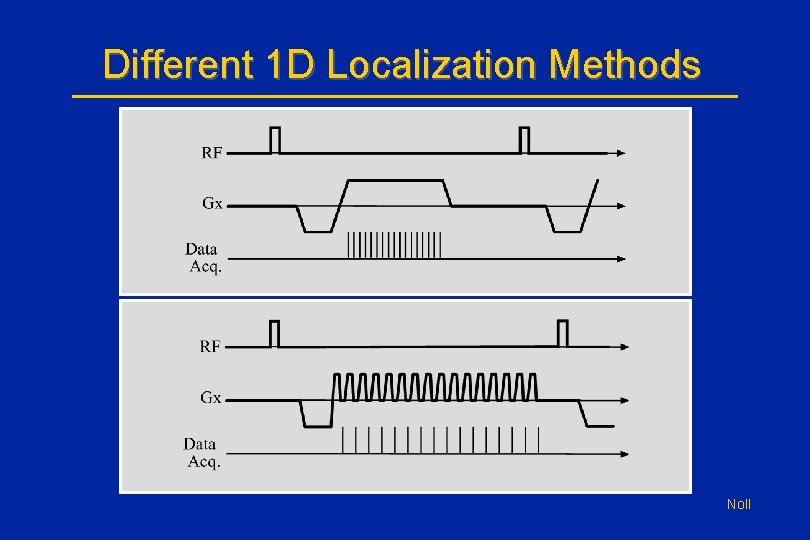
Different 1 D Localization Methods • Upper - smooth precession at different frequencies. (frequency encoding) • Lower - precession in small steps, phase contains location info. (phase encoding). • Sampled data is the same (if we neglect T 2). • The Fourier transform creates the 1 D image. Noll

Different 1 D Localization Methods Noll

Alternate Method #2 for 1 D Localization • In the above cases, gradients were turned on and samples were acquired following a single RF excitation pulse. – At different locations spins precessed at different frequencies. – Motion was either smooth or “stop-action. ” • We now look at a situation where a single sample is acquired after each RF pulse. – Spins precess for a particular length of time and then a single sample is acquired. Noll

Alternate Method #2 for 1 D Localization Noll

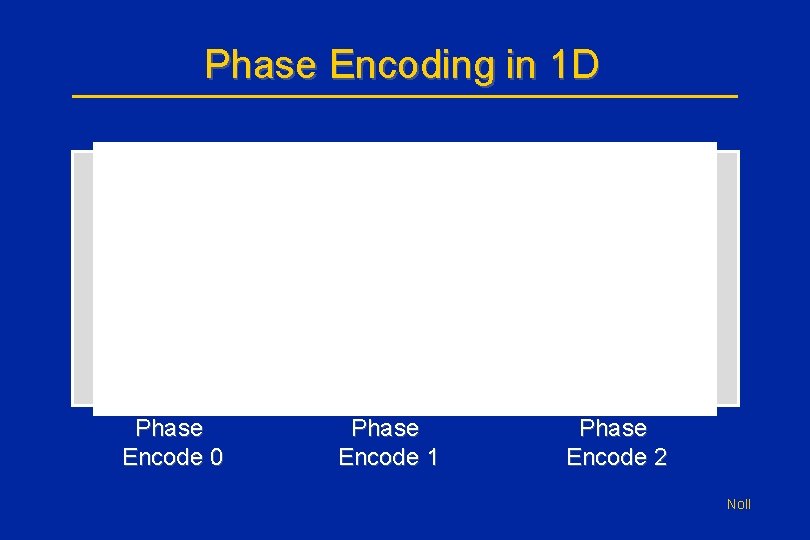
Phase Encoding in 1 D • Again, spins precess only as long as gradient is turned “on. ” • If we look spins after each step (sample location), the precession will again appear as “stop-action” motion. • Again, spatial information has been encoded into the phase of spin. – Another form of “phase encoding. ” Noll

Phase Encoding in 1 D Phase Encode 0 Phase Encode 1 Phase Encode 2 Noll

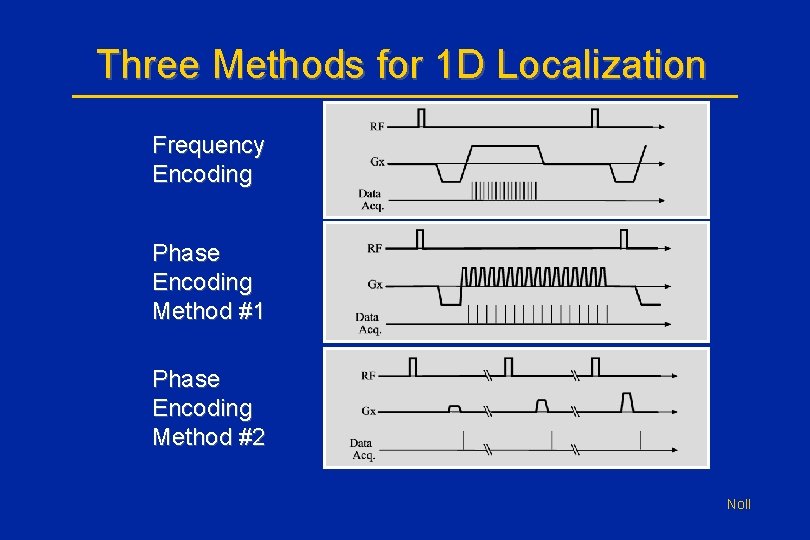
Three Methods for 1 D Localization • 1 D Localization: – – – Frequency encoding Phase encoding following a single RF pulse A single phase encode following each of many RF pulses • Sampled data is the same (if we neglect T 2). • The Fourier transform creates the 1 D image. Noll

Three Methods for 1 D Localization Frequency Encoding Phase Encoding Method #1 Phase Encoding Method #2 Noll

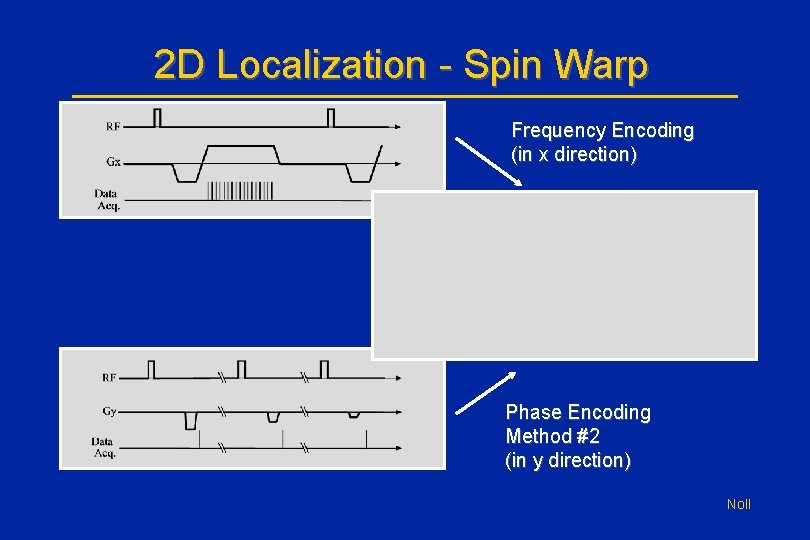
2 D Localization • In general, we will combine two 1 D localization methods to create localization in two dimensions (2 D). • The spin-warp method (used in almost all anatomical MRI) is a combination of : – Frequency encoding in one direction (e. g. Left. Right) – Phase encoding in the other direction (e. g. Anterior -Posterior) Noll

2 D Localization - Spin Warp Frequency Encoding (in x direction) Phase Encoding Method #2 (in y direction) Noll

Spin-Warp Imaging • For each RF pulse: – Frequency encoding is performed in one direction – A single phase encoding value is obtained • With each additional RF pulse: – The phase encoding value is incremented – The phase encoding steps still has the appearance of “stop-action” motion Noll

Spin-Warp Pulse Sequence Noll