An Optimal Minimum Spanning Tree Algorithm Seth Pettie

An Optimal Minimum Spanning Tree Algorithm Seth Pettie and Vijaya Ramachadran Journal of the ACM Vol. 49, No. 1 January 2002, pp. 16 -34

Outline • Preliminary – Cut and Cycle – DJP Algorithm – MST in Dense Case • • Overview of the Algorithm Key Lemma and the Partition Algorithm Decision Tree Conclusion

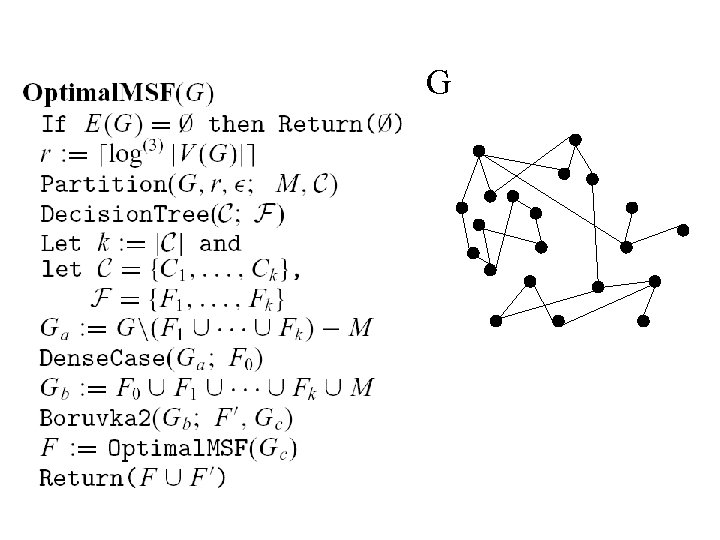
Overview of the Algorithm • Precompute the optimal decision trees for all graphs with ≤ log(3) n vertices • Partition the original graph into small subgraphs – soft heap • Find the MST of each subgraph – decision tree • Use the small MSTs to construct the MST of the original graph – dense case

G

G M C 5 C 1 C 4 C 6 C 2 C 7 C 3

G M C 5 C 1 C 4 C 6 C 2 C 7 C 3 Partition(G, r, ; M, C) • 將問題分成 • Ci裡面 & Ci外面 以Decision. Tree求MSF

G M Partition(G, r, ; M, C) • 將問題分成 • Ci裡面 & Ci外面 以Dense. Case求MSF

• Boruvka 2: • 將vertex數降為 1/4 • Gc: m降為 1/4 • Optimal. MSF(Gc)

Key Lemma • Lemma 3. 2 Let M be a set of edges in a graph G. If C is a subgraph of G that is DJP-contractible w. r. t. G M, then MSF(G) is a subset of DJP-contractible w. r. t G M 即：在G上，使用Soft. Heap， 以Prim algorithm長出來的子圖 Mc : corrupted edges with one endpoint in C

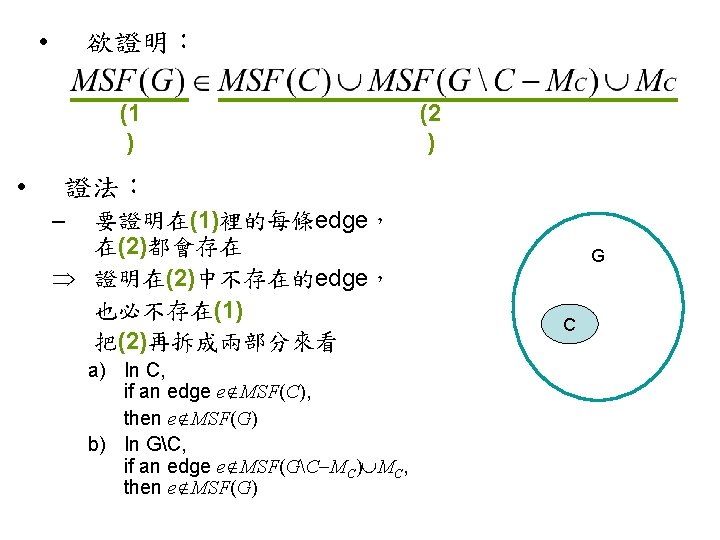
a) 欲證明： In C, if an edge e MSF(C), then e MSF(G) • 證明： – e MSF(C) e must be the heaviest edge on some cycle in C. (cycle property) Such a cycle exists in G as well. So e MSF(G) G C

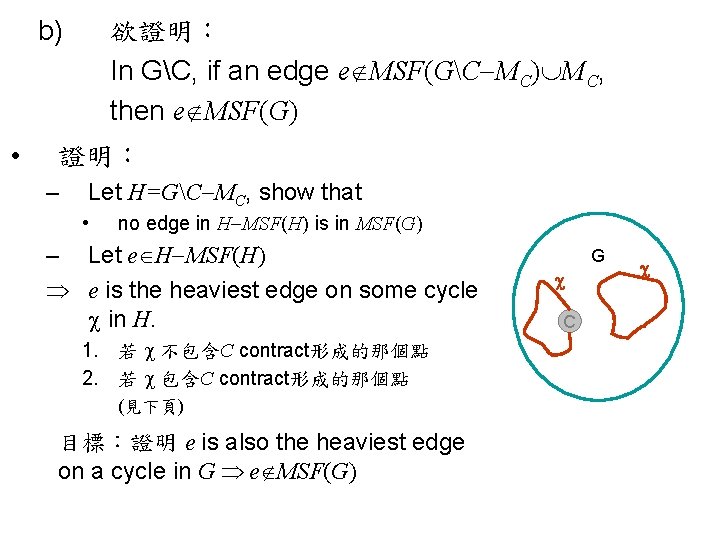
b) • 欲證明： In GC, if an edge e MSF(GC MC) MC, then e MSF(G) 證明： – Let H=GC MC, show that • no edge in H MSF(H) is in MSF(G) – Let e H MSF(H) e is the heaviest edge on some cycle in H. 1. 若 不包含C contract形成的那個點 2. 若 包含C contract形成的那個點 (見下頁) 目標：證明 e is also the heaviest edge on a cycle in G e MSF(G) G C

目標：證明 e is also the heaviest edge on a cycle in G e MSF(G) • 證明 (續上頁)： 2. 若 包含C contract形成的那個點 x, y, w, z: nodes (x, w) and (y, z): end edges of path P Since H includes no corrupted edges with on point in C, so: G-weight of these edges = (G M)-weight T: the spanning tree of C M Q: the path in T connecting x and y g: the heaviest edge in Q. P e w x C w(e) > max(w(x, w), w(y, z)) (def. of e) > (G M)-weight of g (Lemma 2. 1) G-weights of all edges in Q. So, w. r. t. G-weights, e is the heaviest edge on a cycle P Q and cannot be in MSF(G). Q y z

• • 選定一個點為起點， 用DJP演算法長component Ci DJP Ø 長到 1. 大於maxsize, 或 2. 連到別的component Ci 就停下來 insert edges to Soft Heap

Partition & Key Lemma • By applying Key Lemma repeatedly, we see that after Ci is built, the MSF of G is a subset of

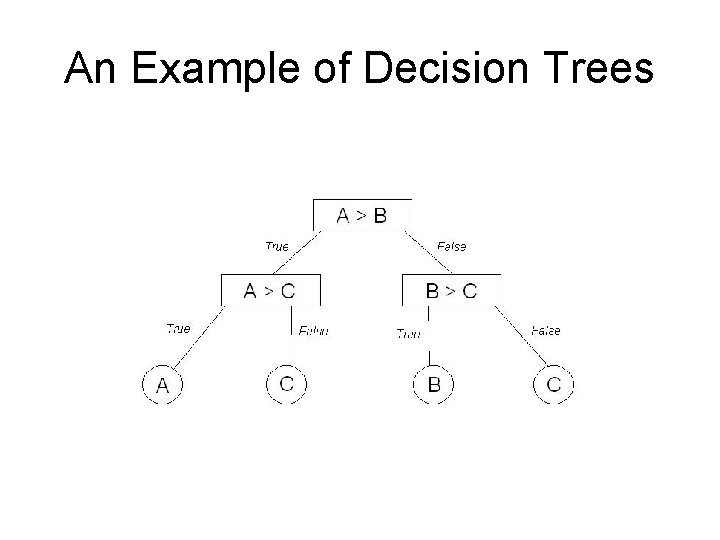
An Example of Decision Trees

MSF Decision Trees • 每個internal node of MSF Decision Trees 上的判斷式是一個edge-weight comparison （對於給定的graph G）。 • 每個internal node of MSF Decision Trees 必恰好有兩個children，分別代表該edgeweight comparison為true或false。 • MSF Decision Trees的leaves列出所有符合 root到每一leaf之路徑上判斷式及其結果的 一些spanning tree。

MSF Decision Trees (cont. ) • Correct MSF Decision Trees的條件為每一 條從root到一個leaf的path可決定唯一的一 個spanning tree為G的MSF。 • Optimal MSF Decision Tree的條件為沒有 比之深度更小的Correct MSF Decision Tree of G存在。 • 當我們有graph G的Optimal MSF Decision Trees，我們就可以將G的edge weight值代 入其判斷式找出其MSF。

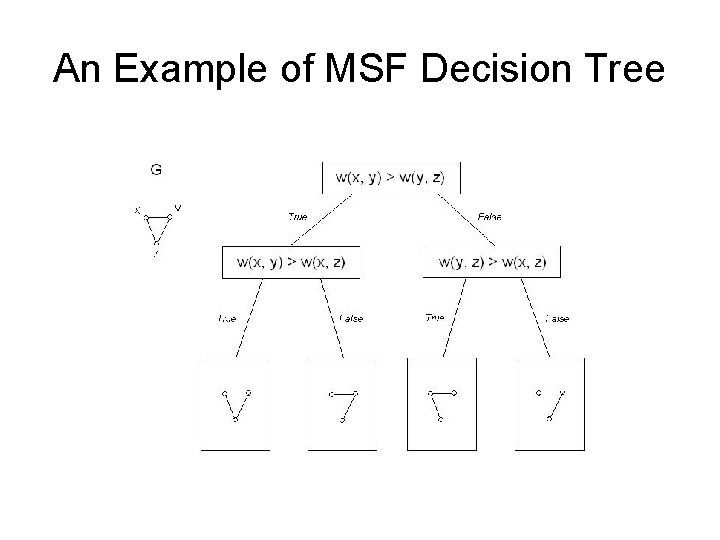
An Example of MSF Decision Tree

Complexity

• Observations: • If T*(m, n) = O(m), then T(m, n)=O(m) • T(m, n)=O(T*(m, n)) for many natural functions for T* (including m (m, n)) • Prove that: T(m, n)=O(T*(m, n)) holds, no matter what describing O(T*(m, n))

• Observations: • If T*(m, n) = O(m), then T(m, n)=O(m) • T(m, n)=O(T*(m, n)) for many natural functions for T* (including m (m, n)) • Prove that: T(m, n)=O(T*(m, n)) holds, no matter what describing O(T*(m, n)) (Skip many propositions , lemmas and corollaries)