An NPComplete Problem The CookLevin theorem 1 Introduction

An NP-Complete Problem The Cook-Levin theorem 1

Introduction • Objectives: – To present the first NP-Complete problem • Overview: – SAT - definition and examples – The Cook-Levin theorem – What next? 2

SAT • Instance: A Boolean formula. • Problem: To decide if the formula is satisfiable. A satisfiable Boolean formula: F T T An unsatisfiable Boolean formula: 3

To Which Time Complexity Class Does SAT Clearly Belong? SAT NP P Co-NP 4

SAT is in NP: Non-Deterministic Algorithm • Guess an assignment to the variables. • Check the assignment. F T x 1 F x 2 T x 3 T T F T T 5

SIP 254 -259 The Cook-Levin Theorem: SAT is NP-Complete Proof Idea: For any NP machine M and any input string w, we construct a Boolean formula M, w which is satisfiable iff M accepts w. . . . 6

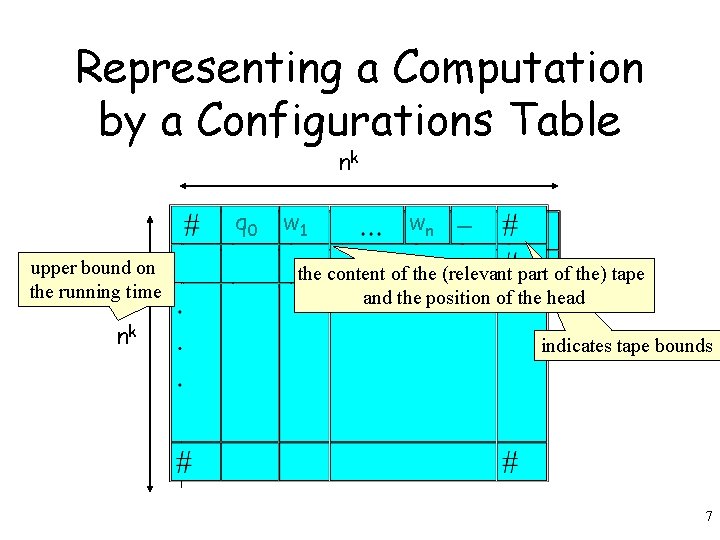
Representing a Computation by a Configurations Table nk qq 0 0 ww 1 1 upper bound on the running time nk wwn n __ the content of the (relevant part of the) tape and the position of the head indicates tape bounds 7

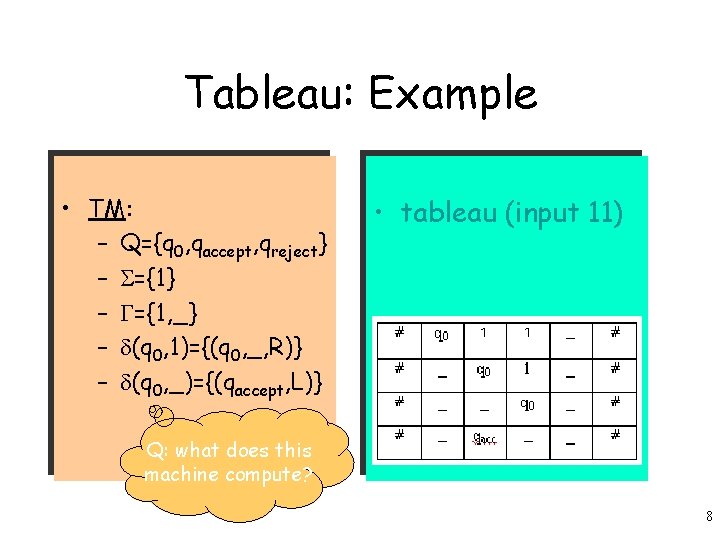
Tableau: Example • TM: – Q={q 0, qaccept, qreject} – ={1, _} – (q 0, 1)={(q 0, _, R)} – (q 0, _)={(qaccept, L)} • tableau (input 11) Q: what does this machine compute? 8

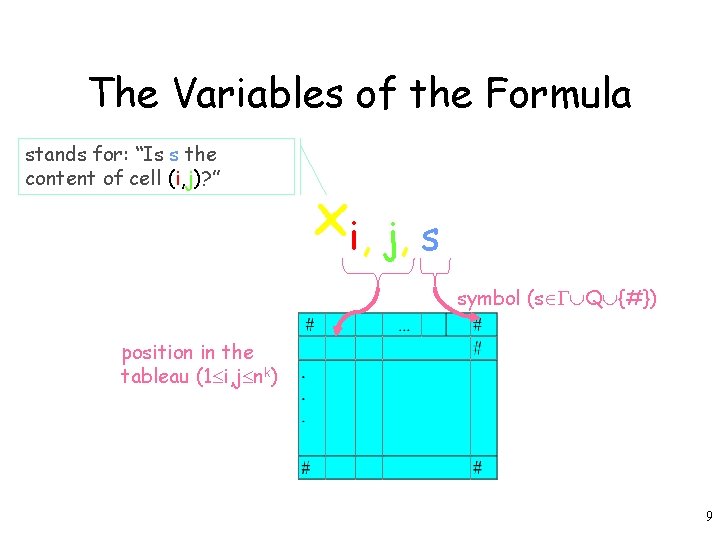
The Variables of the Formula stands for: “Is s the content of cell (i, j)? ” xi, j, s symbol (s Q {#}) position in the tableau (1 i, j nk) 9

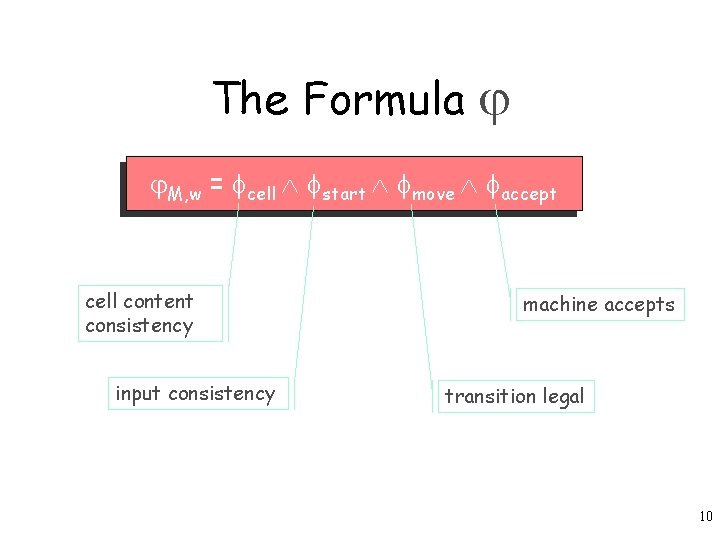
The Formula M, w = cell start move accept cell content consistency input consistency machine accepts transition legal 10

Ensuring Unique Cell Content The (i, j) cell must contain some symbol It shouldn’t contain different symbols. Note: the length of this formula is polynomial in n. 11

Ensuring Initial Configuration Corresponds to Input Observe: we can explicitly state the desired configuration in the first step. Assuming the input string is w 1 w 2. . . wn, 12

Ensuring the Computation Accepts The accepting state is visited during the computation. 13

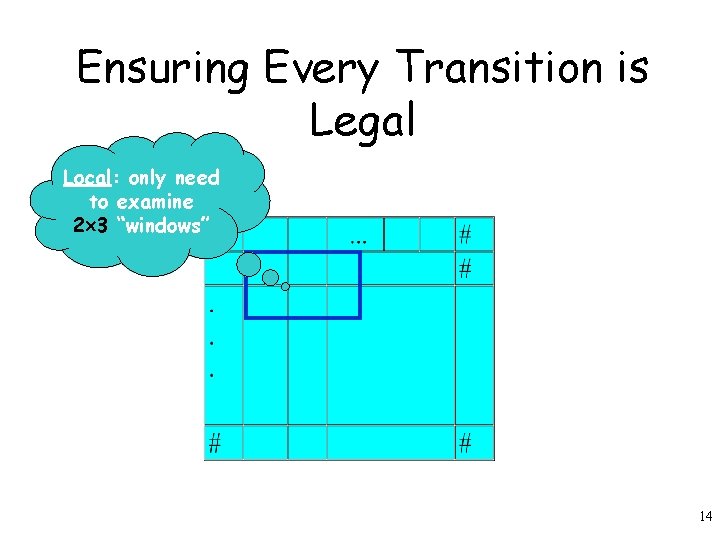
Ensuring Every Transition is Legal Local: only need to examine 2 3 “windows” 14

Which Windows are Legal in the Following Example? • TM: – Q={q 0, qaccept, qreject} – ={1, _} – (q 0, 1)={(q 0, _, R)} – (q 0, _)={(qaccept, L)} 15

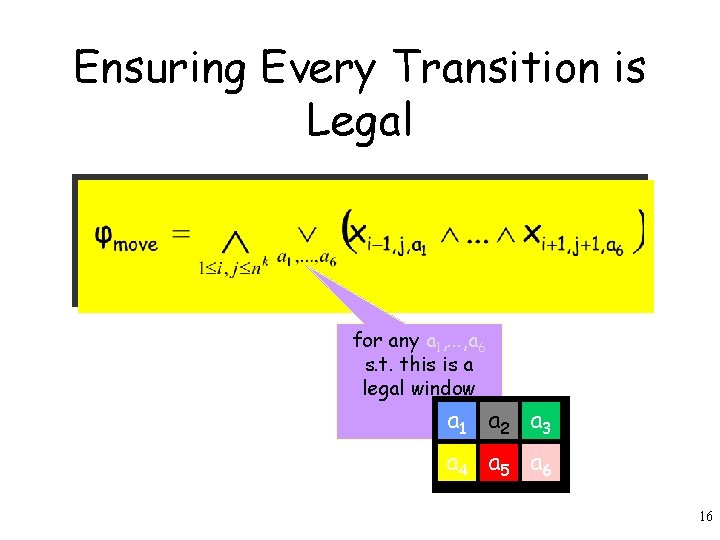
Ensuring Every Transition is Legal for any a 1, . . . , a 6 s. t. this is a legal window a 1 a 2 a 3 a 4 a 5 a 6 16

The Bottom Line M, w = cell start move accept , which is of size polynomial in n - Check! - is satisfiable iff the TM accepts the input string. 17

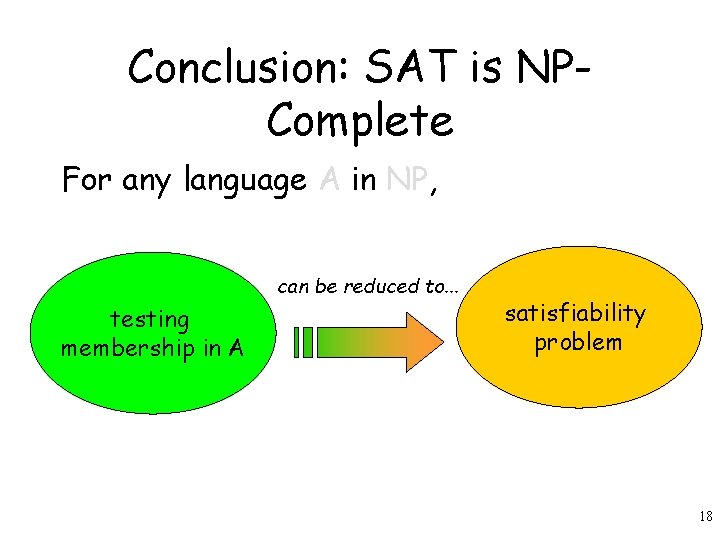
Conclusion: SAT is NPComplete For any language A in NP, can be reduced to. . . testing membership in A satisfiability problem 18

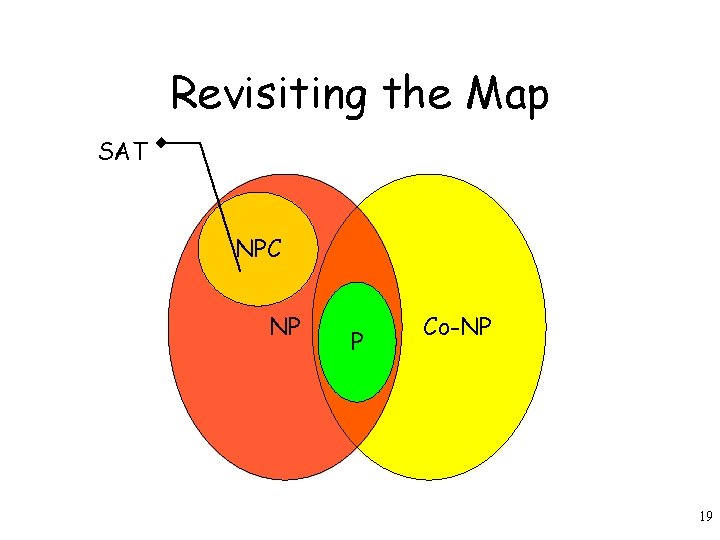
Revisiting the Map SAT NPC NP P Co-NP 19

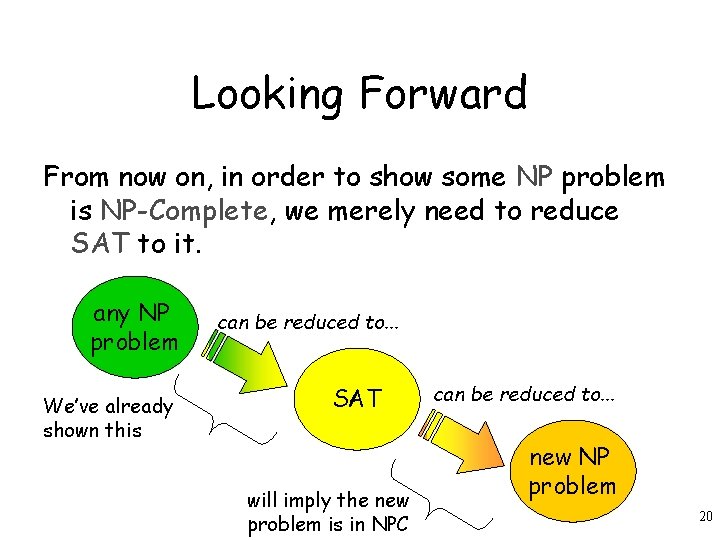
Looking Forward From now on, in order to show some NP problem is NP-Complete, we merely need to reduce SAT to it. any NP problem We’ve already shown this can be reduced to. . . SAT will imply the new problem is in NPC can be reduced to. . . new NP problem 20

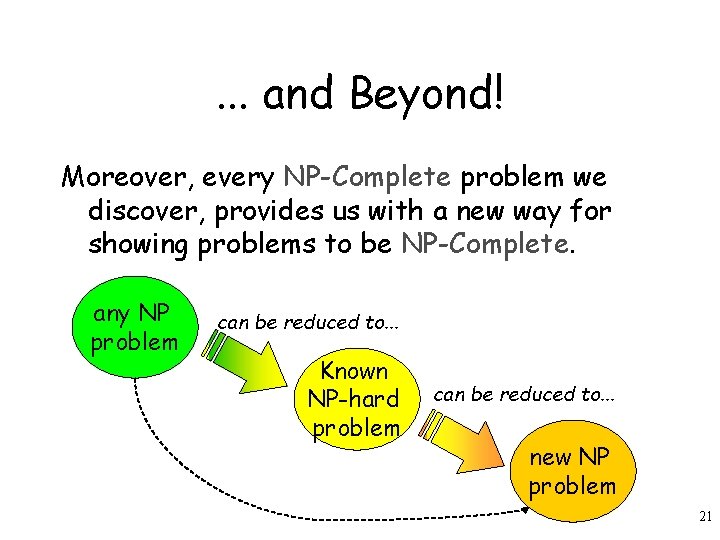
. . . and Beyond! Moreover, every NP-Complete problem we discover, provides us with a new way for showing problems to be NP-Complete. any NP problem can be reduced to. . . Known NP-hard problem can be reduced to. . . new NP problem 21

Summary • We’ve proved SAT is NP-Complete. • We’ve also described a general method for showing other problems are NP-Complete too. 22