An inverse scattering internal multiple elimination method Beyond

An inverse scattering internal multiple elimination method: Beyond attenuation, a new algorithm and initial tests Adriana Citlali Ramírez Arthur B. Weglein Dept. of Physics University of Houston April 2005

Plan for this talk • Report our initial efforts to address the removal of internal multiples. • 1 -D numerical examples • Future Work

Why? • There is a current significant challenge of producing effective methods for attenuating and eliminating internal multiples under circumstances where the ability to determine the velocity is far from adequate. • The industry trend to deep water and exploration beneath complex and ill-defined geologic overburdens (i. e. salt, basalt and karsted sediments). • There are circumstances when it is necessary and useful to go beyond reducing internal multiples.

Objectives • Seek to improve the effectiveness of the inverse scattering internal multiple attenuator by studying higher order terms, without knowing or determining the medium properties.

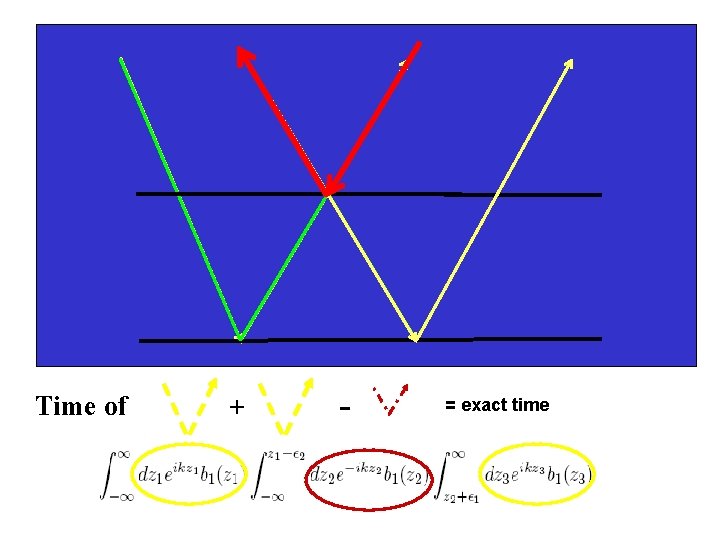
Time of + - = exact time

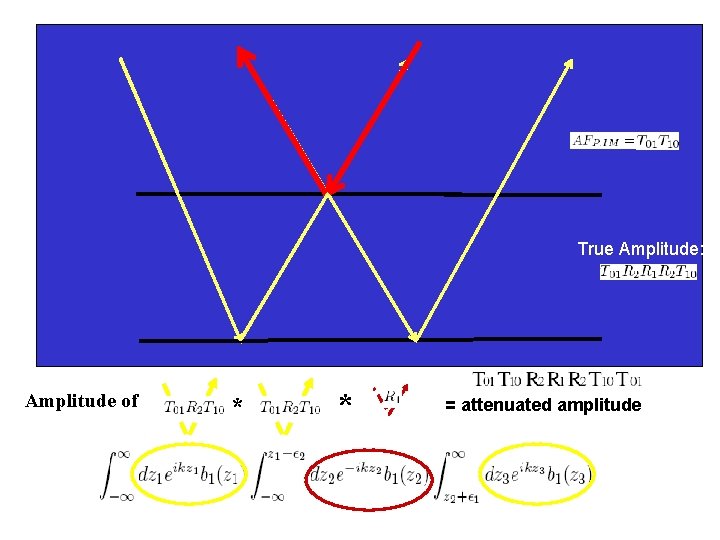
True Amplitude: Amplitude of * * = attenuated amplitude

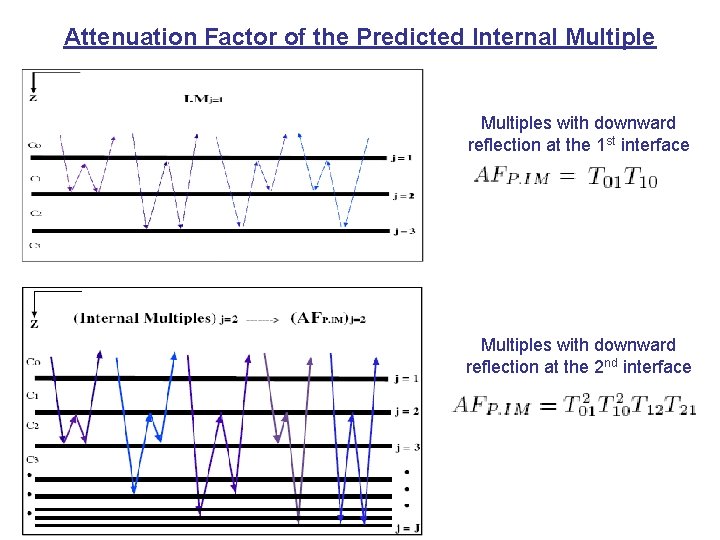
Attenuation Factor of the Predicted Internal Multiples with downward reflection at the 1 st interface Multiples with downward reflection at the 2 nd interface

Elimination Series The predicted amplitude should have the true amplitude of the multiple in the data. 1 Seek to determine how and where the removal process might reside in the inverse series with a simple example. We need to find the series that does:

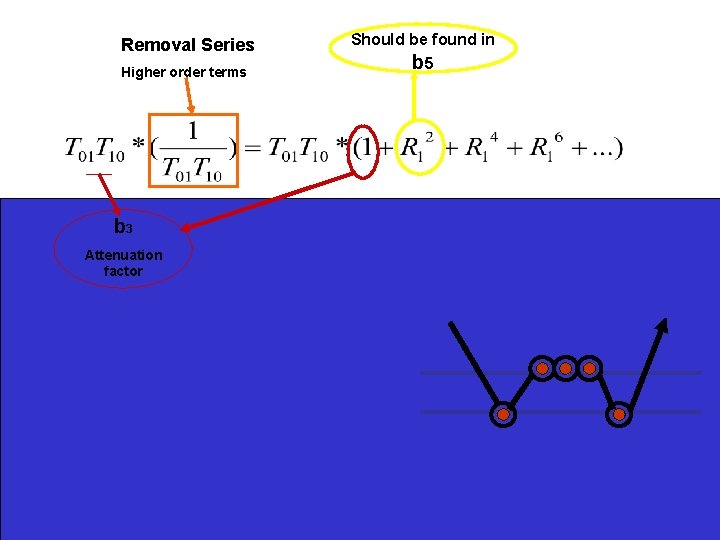
Removal Series Higher order terms b 3 Attenuation factor Should be found in b 5

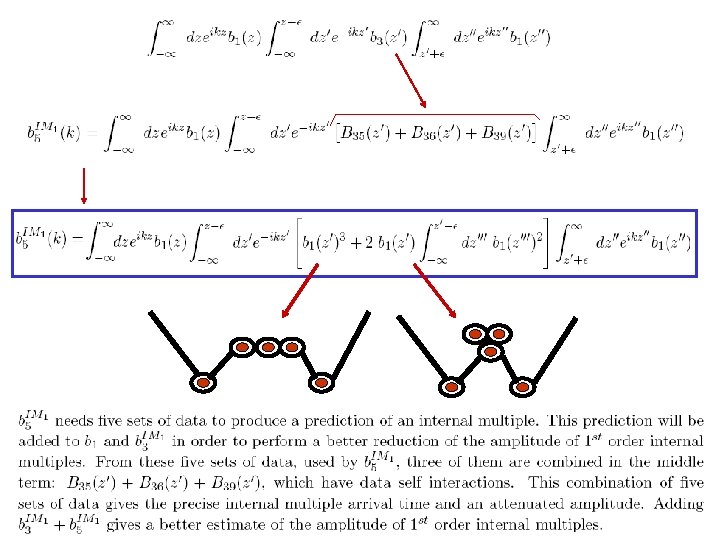
The Fifth Term

The Fifth Term Write it in terms of effective data.

The Fifth Term

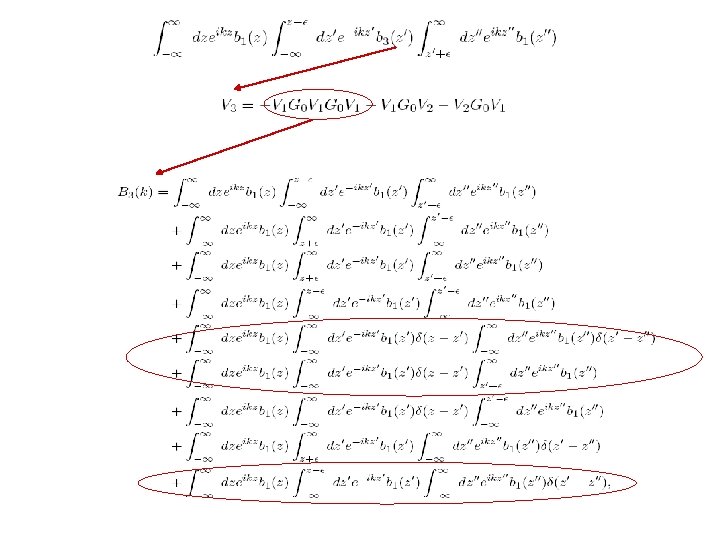
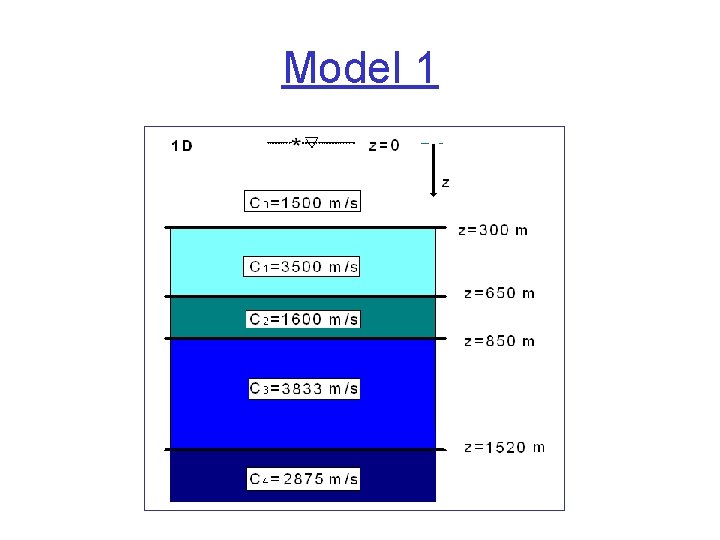
Model 1

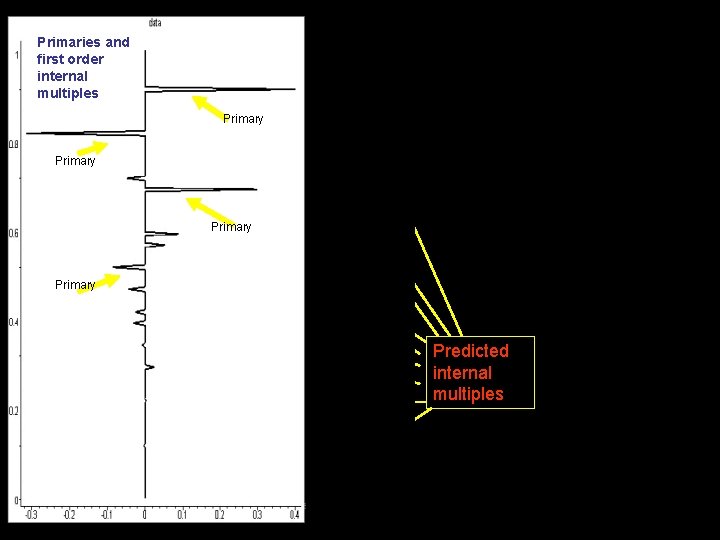
Primaries and first order internal multiples b 3 Primary Predicted internal multiples This is the result after the addition b 1+b 3

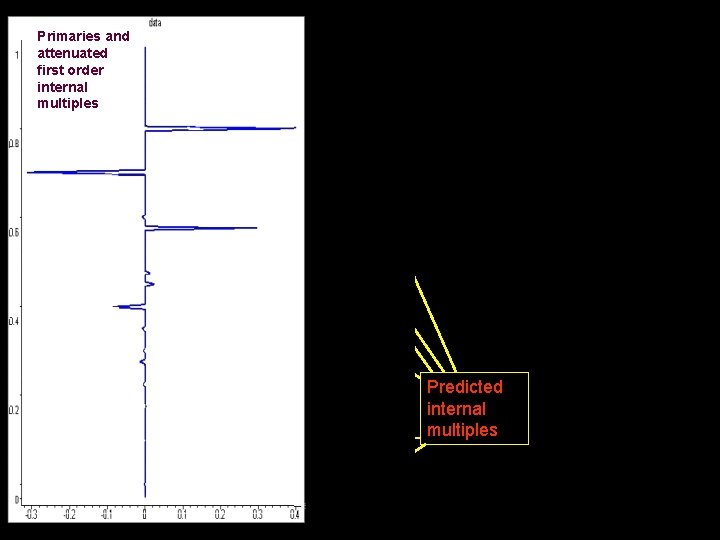
Primaries and attenuated first order internal multiples b 5 Predicted internal multiples This is the result after the addition b 1+b 3+b 5

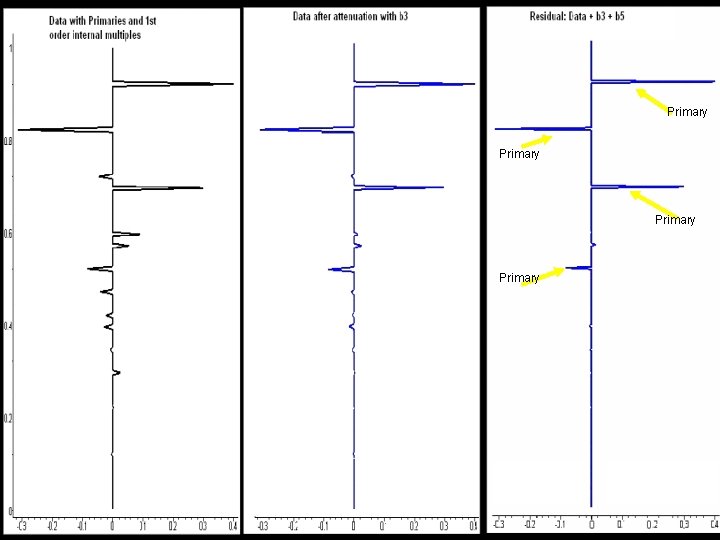
Primary

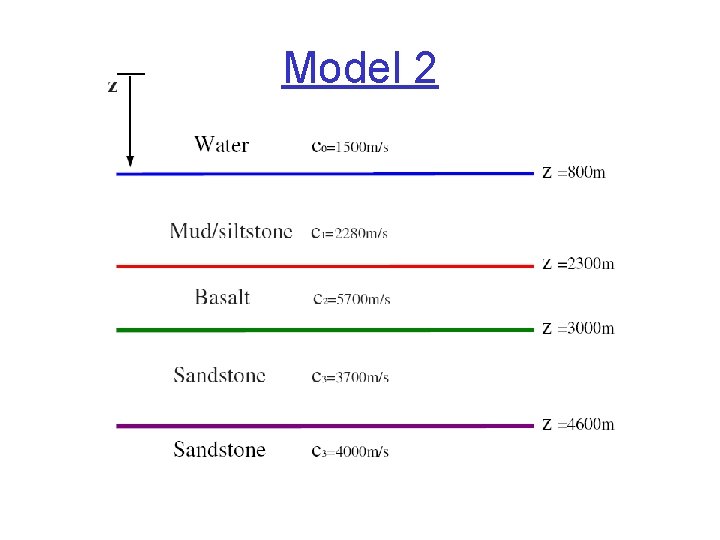
Model 2

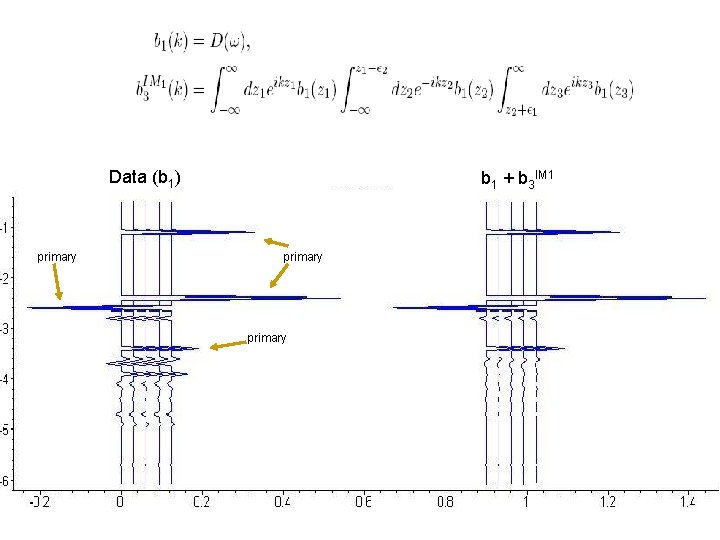
Data (b 1) primary b 1 + b 3 IM 1 primary

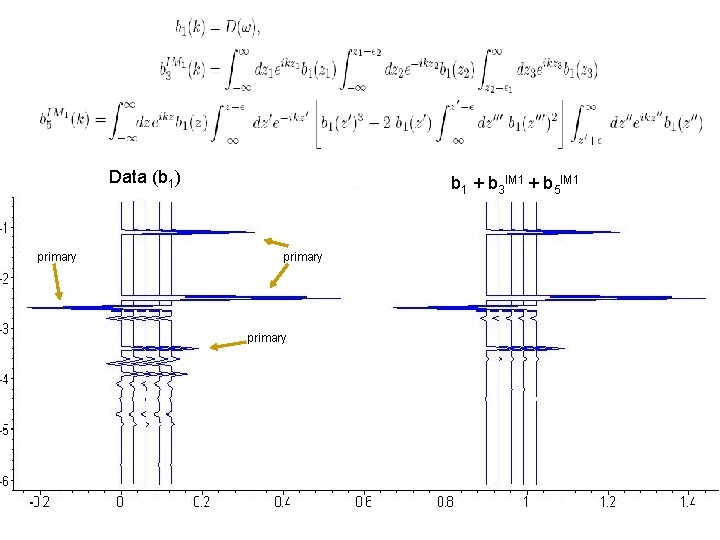
Data (b 1) primary b 1 + b 3 IM 1 + b 5 IM 1 primary

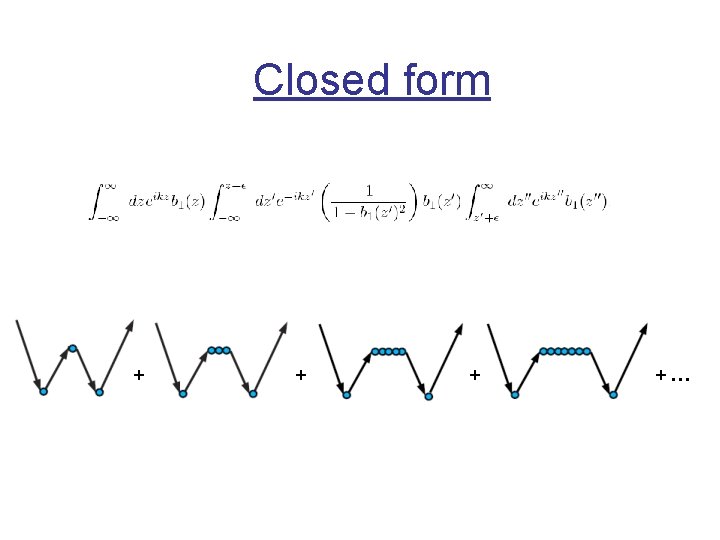
Closed form + +…

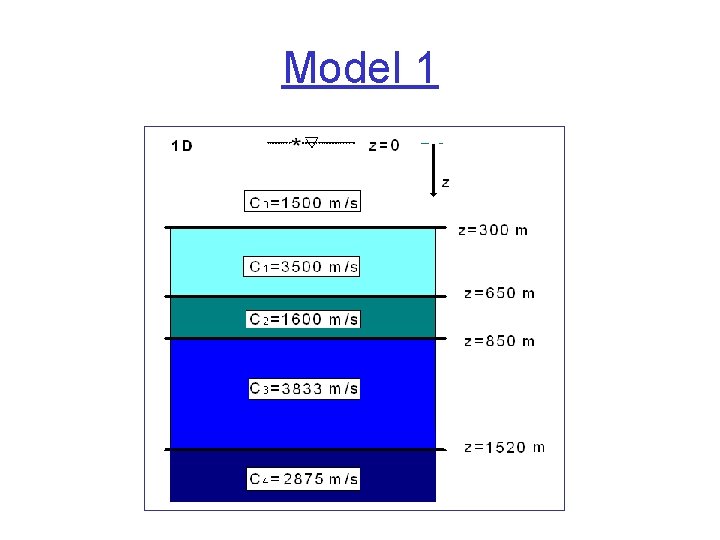
Model 1

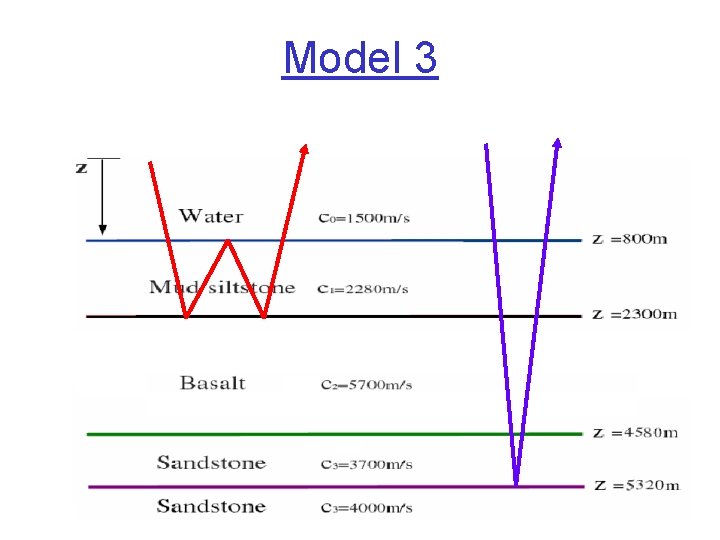
Model 3

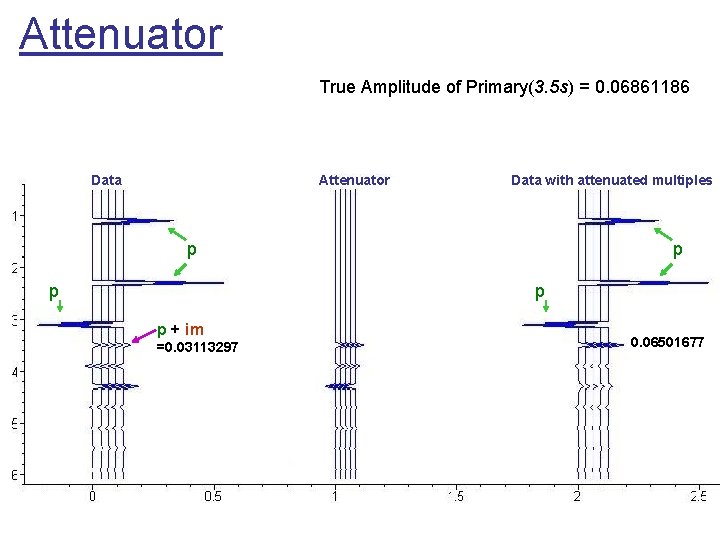
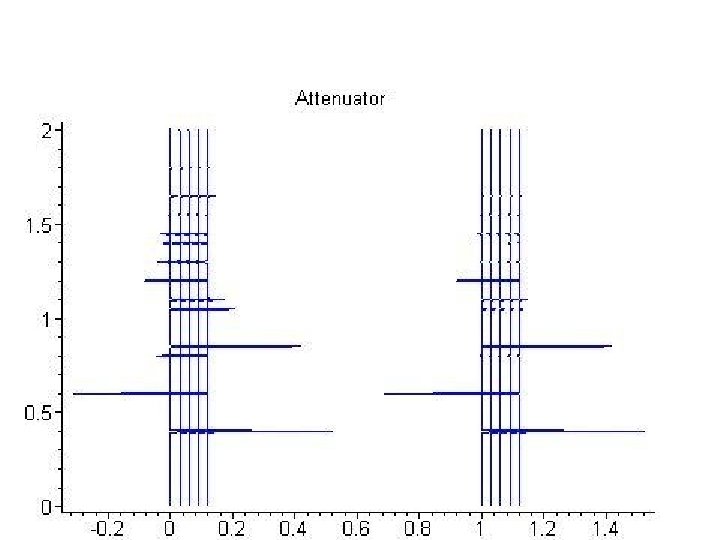
Attenuator True Amplitude of Primary(3. 5 s) = 0. 06861186 Data Attenuator Data with attenuated multiples p p p + im =0. 03113297 0. 06501677

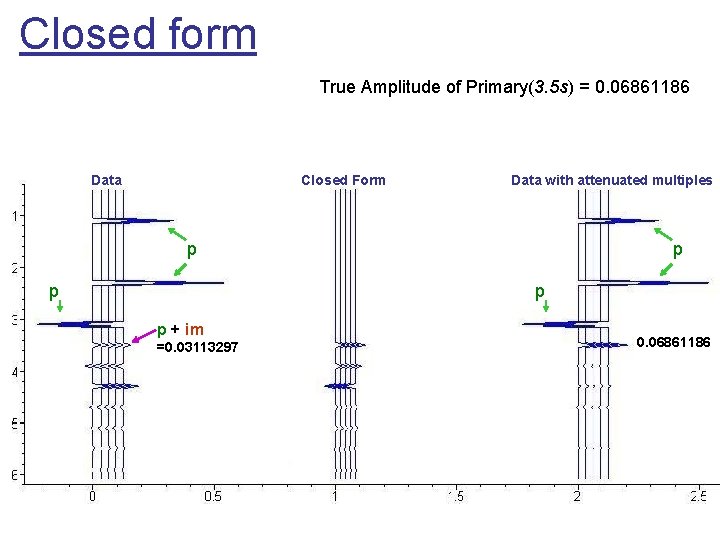
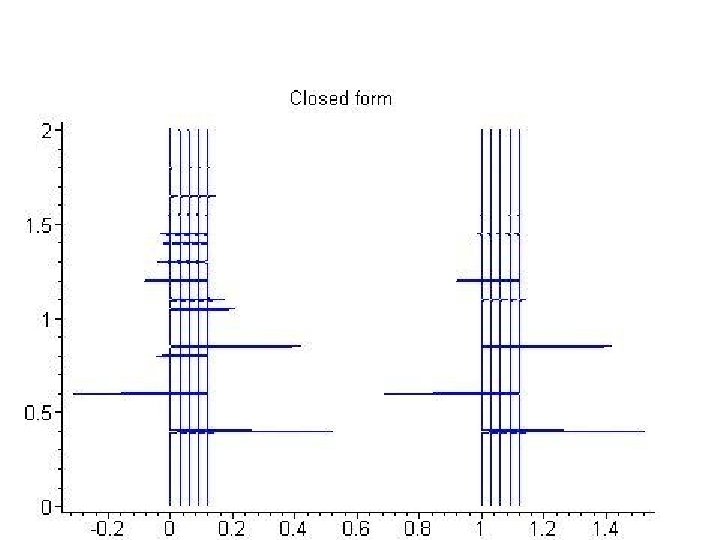
Closed form True Amplitude of Primary(3. 5 s) = 0. 06861186 Data Closed Form Data with attenuated multiples p p p + im =0. 03113297 0. 06861186

Attenuator Closed form (b. IM 1)LO=

Conclusions • The first term in the removal series is an attenuator. It predicts the perfect time and always significantly reduces but doesn’t eliminate the 1 st order internal multiples. • Higher order terms towards elimination are determined by distinct non-linear mathematical expressions that only involve the measured data and the reference medium. • The removal series for 1 st order internal multiples, based on inverse scattering theory, has been identified. • A closed form for the leading order subseries was obtained and used in examples.

Acknowledgments • We acknowledge and thank all the sponsors and members of M-OSRP for the support of this research. • Simon Shaw (Conoco. Phillips), Einar Otnes (Statoil) and Bogdan Nita (M-OSRP)are thanked for useful comments and suggestions.

Future Plans