An Inverse Model Reduction Method for Finite Element

An Inverse Model Reduction Method for Finite Element Model Updating in Structural Health Monitoring Benedikt Hofmeister 1, Marlene Bruns 1, Tanja Grießmann 1, Ingo Gebauer 2 and Raimund Rolfes 1 [1] Leibniz University Hannover/For. Wind, Germany – Institute of Structural Analysis [2] Fraunhofer-Institut für Windenergiesysteme IWES, Germany © For. Wind @For. Wind_DE 1

Contents • Motivation • State of the Art – Cross-Sectional Analysis • Inverse Model Reduction • Application • Summary and Outlook © For. Wind @For. Wind_DE 2

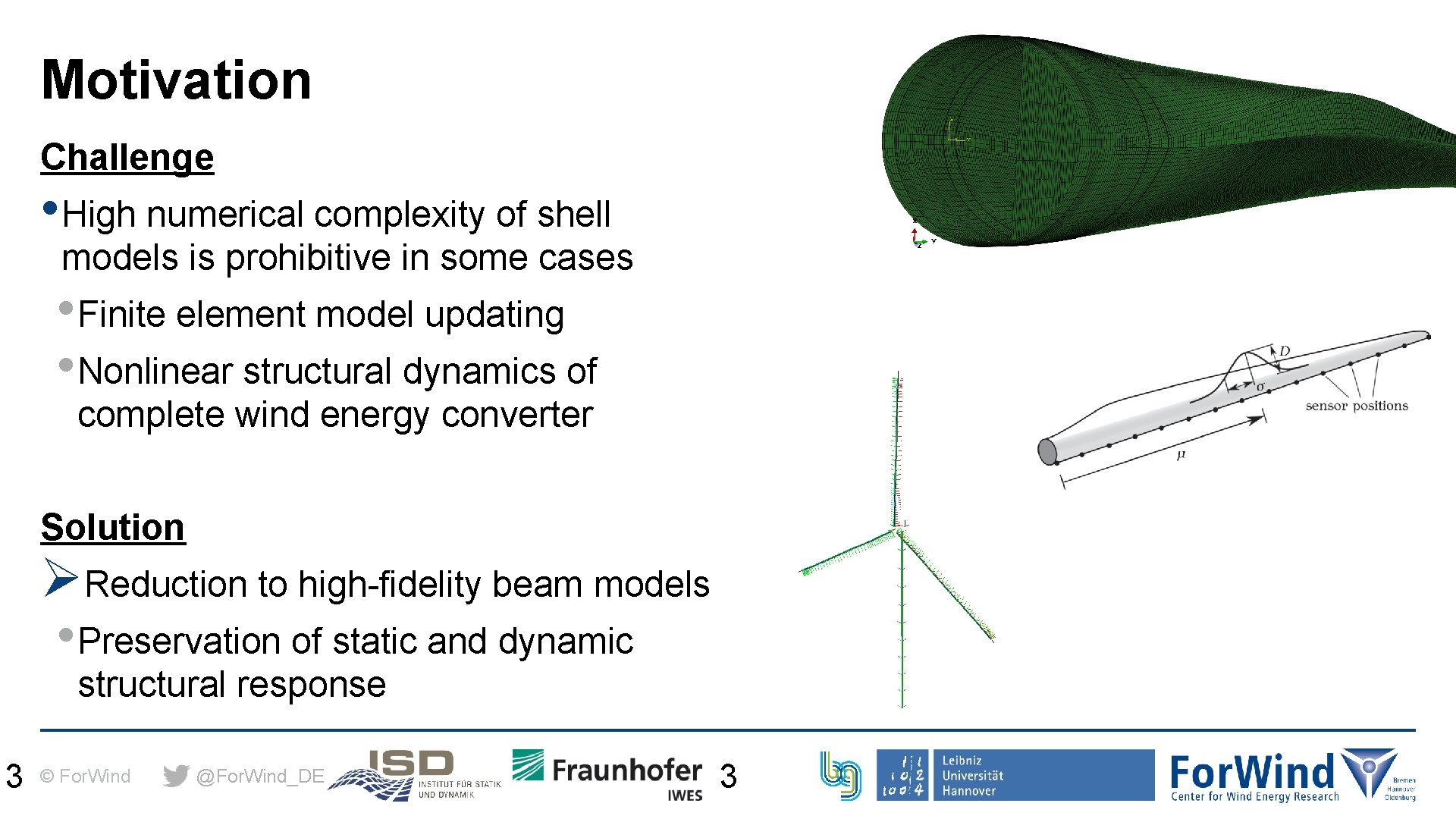
Motivation Challenge • High numerical complexity of shell models is prohibitive in some cases • Finite element model updating • Nonlinear structural dynamics of complete wind energy converter Solution ØReduction to high-fidelity beam models • Preservation of static and dynamic structural response 3 © For. Wind @For. Wind_DE 3

State of the Art Cross-Sectional Analysis for Rotor Blades • Finite element calculation of multiple 2 D cross sections alongitudinal axis • EIxx, EIyy, EIxy • GA, EA • Selection of Software • BECAS (DTU), Pre. Comp (NREL), FOCUS (IWES) Holm-Jørgensen, 2009: Nonlinear Multibody Dynamics of Wind Turbines, Ph. D Thesis Limitations ØHigh number of elements required for accurate results ØTransformation of blade design layup data necessary 4 © For. Wind @For. Wind_DE 4

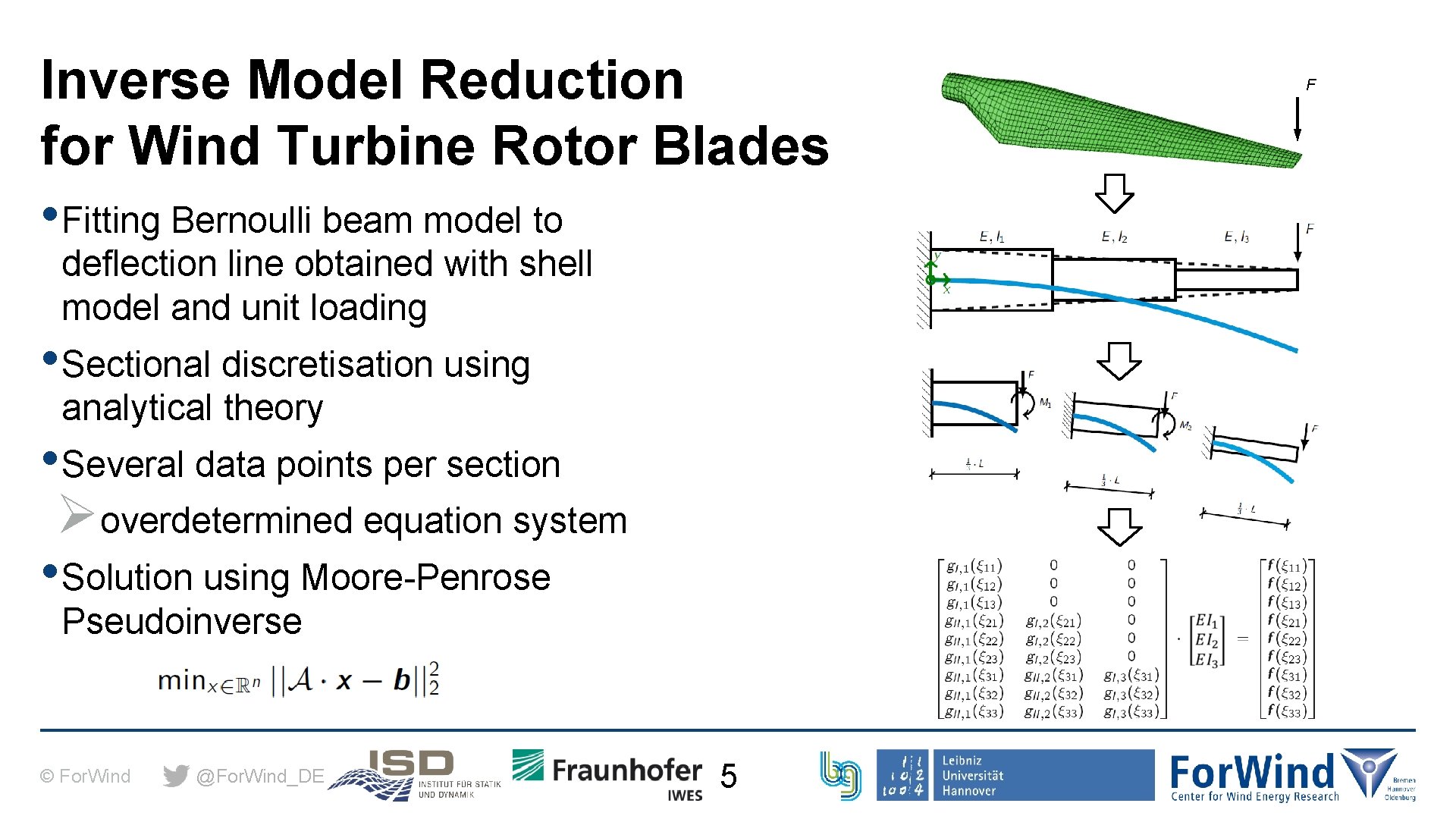
Inverse Model Reduction for Wind Turbine Rotor Blades • Fitting Bernoulli beam model to F deflection line obtained with shell model and unit loading • Sectional discretisation using analytical theory • Several data points per section Øoverdetermined equation system • Solution using Moore-Penrose Pseudoinverse © For. Wind @For. Wind_DE 5

Application & Comparison (1) • FE models • Shell model of 40 -m wind turbine rotor blade • Beam model obtained with cross-sectional shell model analysis • Beam model obtained with inverse reduction cross-sectional beam model • Static and dynamic response obtained using ABAQUS inversely reduced beam model • Cubic shear stiff beam elements B 33 © For. Wind @For. Wind_DE 6

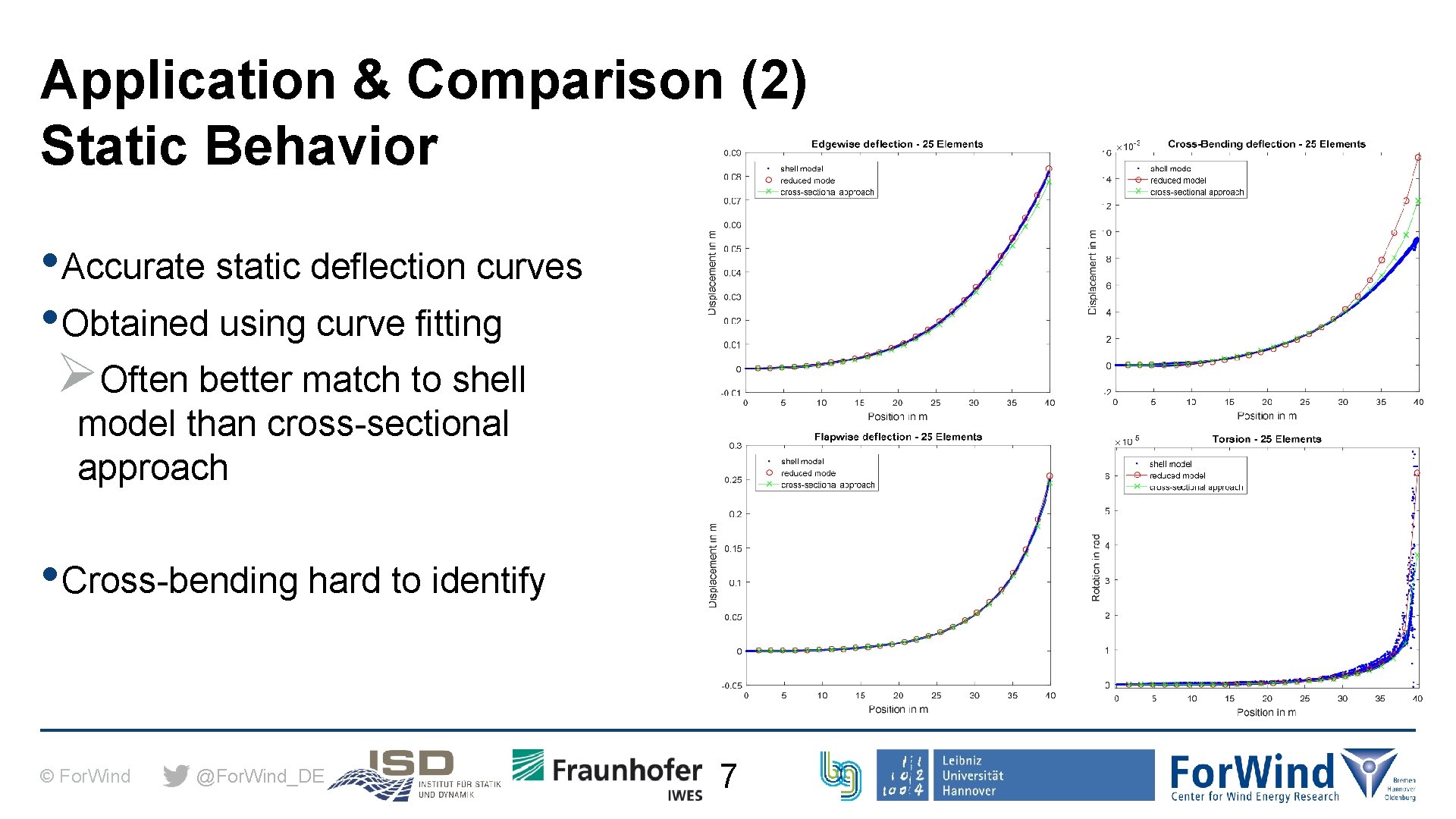
Application & Comparison (2) Static Behavior • Accurate static deflection curves • Obtained using curve fitting ØOften better match to shell model than cross-sectional approach • Cross-bending hard to identify © For. Wind @For. Wind_DE 7

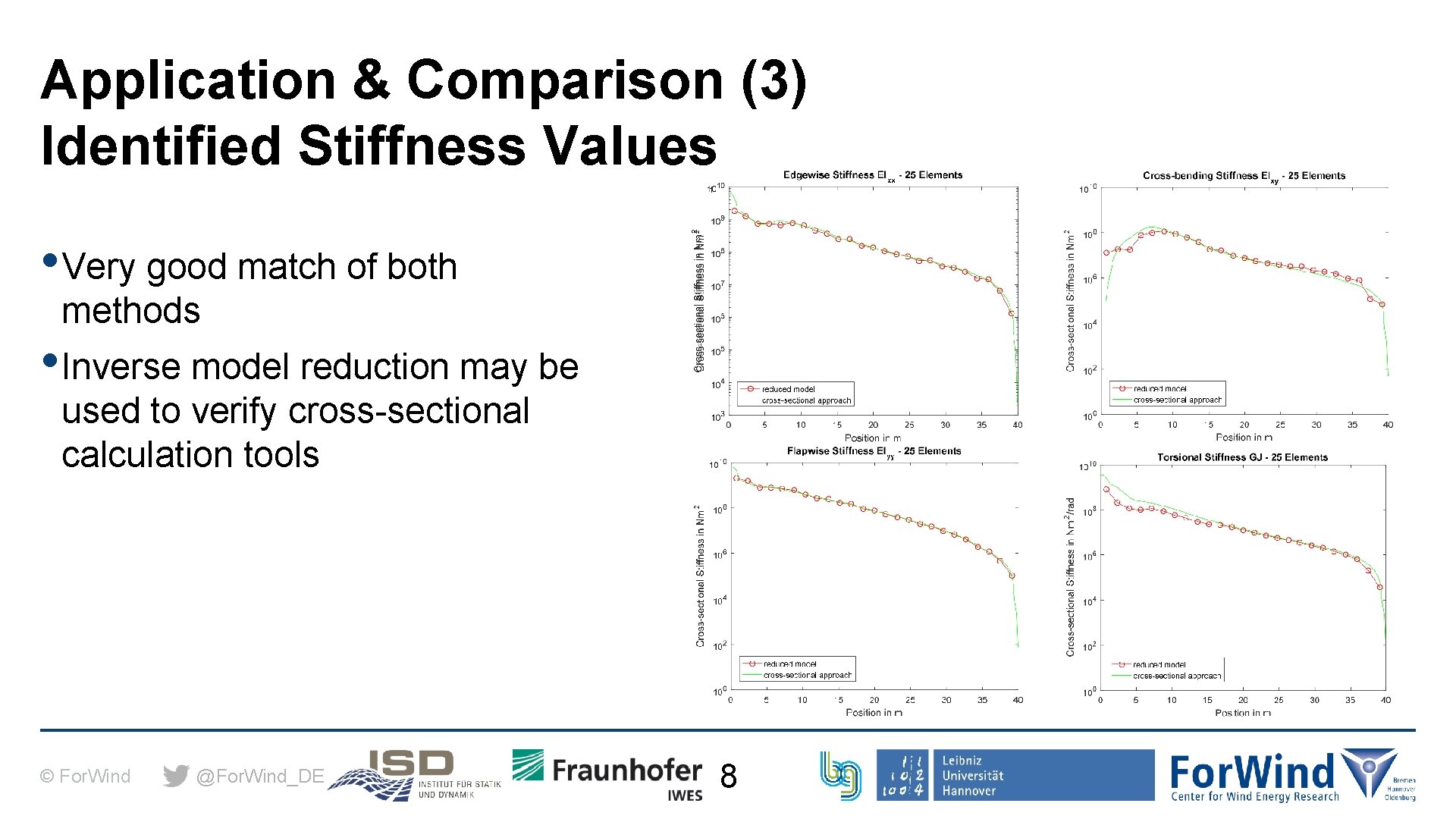
Application & Comparison (3) Identified Stiffness Values • Very good match of both methods • Inverse model reduction may be used to verify cross-sectional calculation tools © For. Wind @For. Wind_DE 8

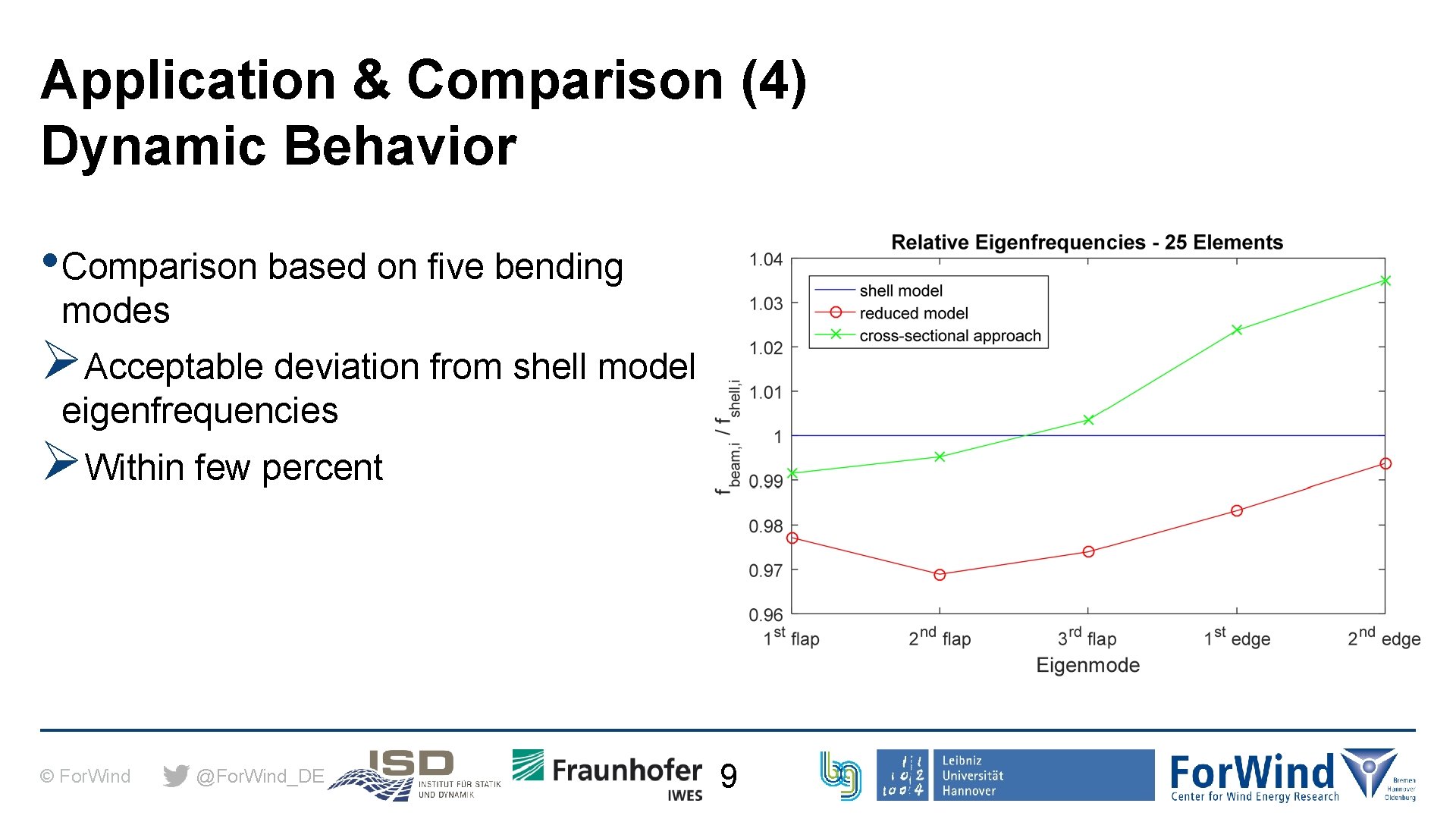
Application & Comparison (4) Dynamic Behavior • Comparison based on five bending modes ØAcceptable deviation from shell model eigenfrequencies ØWithin few percent © For. Wind @For. Wind_DE 9

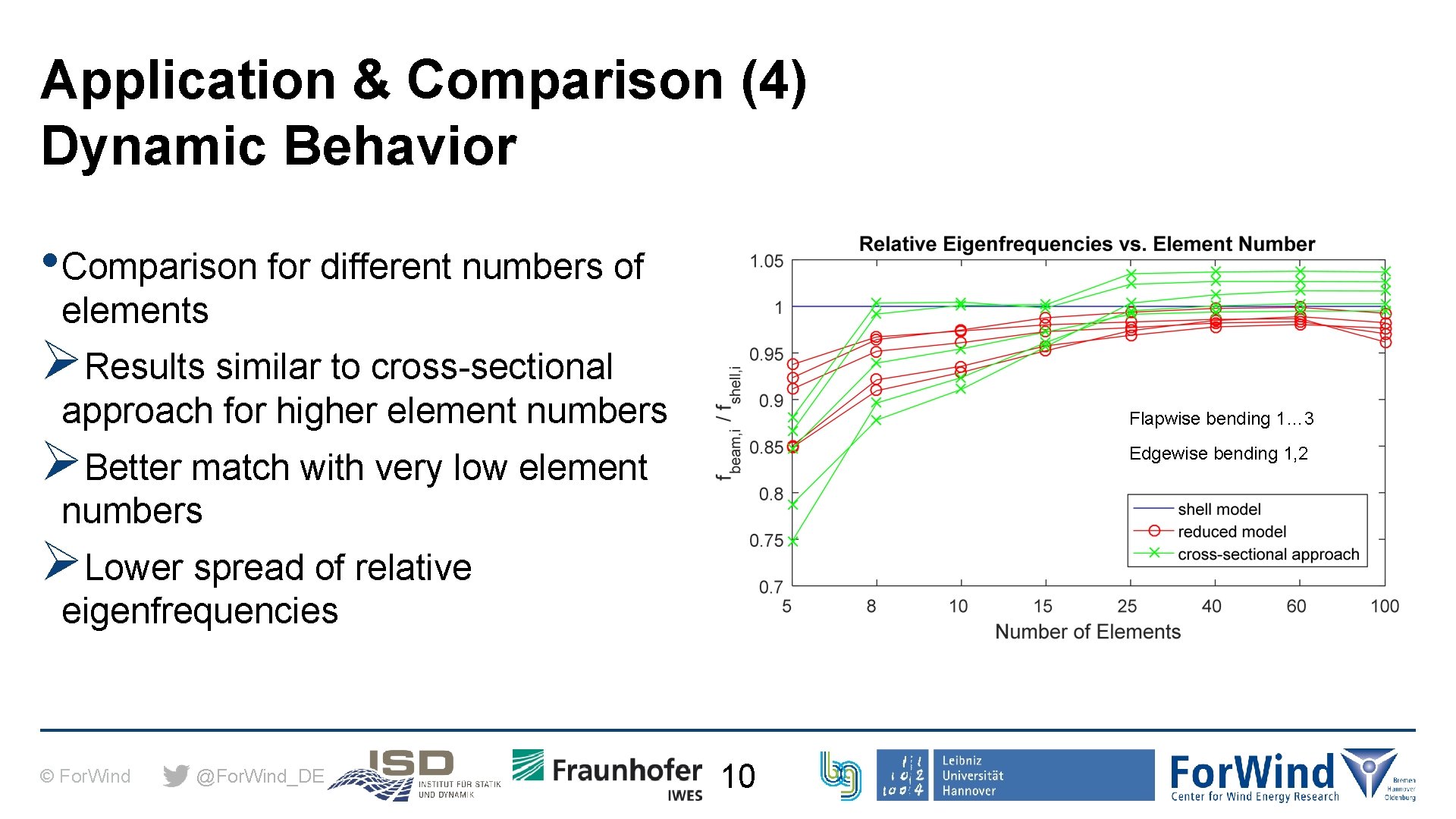
Application & Comparison (4) Dynamic Behavior • Comparison for different numbers of elements ØResults similar to cross-sectional approach for higher element numbers Flapwise bending 1… 3 ØBetter match with very low element Edgewise bending 1, 2 numbers ØLower spread of relative eigenfrequencies © For. Wind @For. Wind_DE 10

Summary • Inverse model reduction on basis of deflection curves ØReduction to very few elements possible ØPreservation of global static and dynamic behavior • Better fidelity than cross-sectional approach with low element counts ØPotential speedup for numerical models ØTransformation of blade design layup data can be avoided © For. Wind @For. Wind_DE 11

Outlook • Application to measured deflection / slope curves ØEstimate as-built stiffness distribution in finished blades • Estimation of mass distribution ØPitch rotation of blade in earth’s gravitational field provides load cases • Identify warping properties / open cross-sections ØBend-twist coupling behavior for beam kinematics © For. Wind @For. Wind_DE 12

Questions to you all • Anyone in audience interested in this method? ØDo you know someone who might be? ØResearch paper • Applicable in practice? • Further applications I did not think of? © For. Wind @For. Wind_DE 13

Thank you for your attention! © For. Wind @For. Wind_DE 14