An Introduction to Voting Theory History and Procedures



![Top Six Voting Systems [continued] Voting systems include rules for Vote Endowment: number of Top Six Voting Systems [continued] Voting systems include rules for Vote Endowment: number of](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-4.jpg)
![Top Six Voting Procedures [continued] Plurality Voting Endowment: One vote for the most preferred Top Six Voting Procedures [continued] Plurality Voting Endowment: One vote for the most preferred](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-6.jpg)

![Top Six Voting Procedures [continued] Borda Voting Endowment: Assign ranks to choices Allocation: Trading/saving Top Six Voting Procedures [continued] Borda Voting Endowment: Assign ranks to choices Allocation: Trading/saving](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-9.jpg)
![Borda and Rankings [continued] Not used this way © 2004. Arnold B. Urken All Borda and Rankings [continued] Not used this way © 2004. Arnold B. Urken All](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-12.jpg)
![Top Six Voting Procedures [continued] Condorcet Scoring Endowment: Ordinal rankings assigned to choices Allocation: Top Six Voting Procedures [continued] Condorcet Scoring Endowment: Ordinal rankings assigned to choices Allocation:](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-13.jpg)
![Top Seven Voting Procedures [continued] Copeland Scoring Endowment: Ordinal rankings assigned to choices Allocation: Top Seven Voting Procedures [continued] Copeland Scoring Endowment: Ordinal rankings assigned to choices Allocation:](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-15.jpg)
![Top Seven Voting Procedures [continued] Approval Voting Endowment: N votes where N = number Top Seven Voting Procedures [continued] Approval Voting Endowment: N votes where N = number](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-17.jpg)
![Top Seven Voting Procedures [continued] Observations about Approval Voting n Empirical observation: Voters cast Top Seven Voting Procedures [continued] Observations about Approval Voting n Empirical observation: Voters cast](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-19.jpg)
![Top Seven Voting Procedures [continued] STV (IRV--Proportional Representation) Endowment: Assign ranks to choices Allocation: Top Seven Voting Procedures [continued] STV (IRV--Proportional Representation) Endowment: Assign ranks to choices Allocation:](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-20.jpg)

![Pre-18 th Century Voting Theory [continued] n Pliny the Younger n Ramon Lull n Pre-18 th Century Voting Theory [continued] n Pliny the Younger n Ramon Lull n](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-26.jpg)
![Pre-18 th Century Voting Theory [continued] n Pliny the Younger n Letter to Titius Pre-18 th Century Voting Theory [continued] n Pliny the Younger n Letter to Titius](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-27.jpg)
![Pre-18 th Century Voting Theory [continued] n Execution faction leader leads switch from death Pre-18 th Century Voting Theory [continued] n Execution faction leader leads switch from death](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-28.jpg)
![Pre-18 th Century Voting Theory [continued] n Pliny calls for ternary vote (with division Pre-18 th Century Voting Theory [continued] n Pliny calls for ternary vote (with division](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-29.jpg)
![Pre-18 th Century Voting Theory [continued] n Why? n Neither Acquittal nor Death would Pre-18 th Century Voting Theory [continued] n Why? n Neither Acquittal nor Death would](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-30.jpg)
![Pre-18 th Century Voting Theory [continued] n Issues Raised n Sincere voting: honest communication Pre-18 th Century Voting Theory [continued] n Issues Raised n Sincere voting: honest communication](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-31.jpg)
![Pre-18 th Century Voting Theory [continued] Ramon Lull A. D. 1232 -1316 n Explored Pre-18 th Century Voting Theory [continued] Ramon Lull A. D. 1232 -1316 n Explored](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-32.jpg)
![Pre-18 th Century Voting Theory [continued] Blanquerna (1285) n Mixed method (“art”) Borda and Pre-18 th Century Voting Theory [continued] Blanquerna (1285) n Mixed method (“art”) Borda and](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-33.jpg)
![Pre-18 th Century Voting Theory [continued] De Arte Eleccionis (1299) n Condorcet scoring n Pre-18 th Century Voting Theory [continued] De Arte Eleccionis (1299) n Condorcet scoring n](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-34.jpg)
![Pre-18 th Century Voting Theory [continued] Nicolaus Cusanus (1430) n Goal: design an “honest” Pre-18 th Century Voting Theory [continued] Nicolaus Cusanus (1430) n Goal: design an “honest”](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-35.jpg)
![Pre-18 th Century Voting Theory [continued] The Venetian Method (13 th Century) n Similar Pre-18 th Century Voting Theory [continued] The Venetian Method (13 th Century) n Similar](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-36.jpg)

![18 th Century France: The Golden Age? [continued] Voting in the French Academy of 18 th Century France: The Golden Age? [continued] Voting in the French Academy of](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-38.jpg)
![18 th Century France: The Golden Age? [continued] Voting in the French Academy of 18 th Century France: The Golden Age? [continued] Voting in the French Academy of](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-39.jpg)
![18 th Century France: The Golden Age? [continued] Voting in the French Academy of 18 th Century France: The Golden Age? [continued] Voting in the French Academy of](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-40.jpg)
![18 th Century France: The Golden Age? [continued] Voting in the French Academy of 18 th Century France: The Golden Age? [continued] Voting in the French Academy of](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-41.jpg)
![18 th Century France: The Golden Age? [continued] Condorcet and the French Revolution n 18 th Century France: The Golden Age? [continued] Condorcet and the French Revolution n](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-43.jpg)
![18 th Century France: The Golden Age? [continued] Daunou and after n FAS becomes 18 th Century France: The Golden Age? [continued] Daunou and after n FAS becomes](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-44.jpg)
![18 th Century France: The Golden Age? [continued] Daunou and after (continued) n Voting 18 th Century France: The Golden Age? [continued] Daunou and after (continued) n Voting](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-45.jpg)
![18 th Century France: The Golden Age? [continued] Daunou and after (continued) n Proportional 18 th Century France: The Golden Age? [continued] Daunou and after (continued) n Proportional](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-46.jpg)

![The Rediscovery of Voting Theory [continued] Arrow n Relies on Black to understand Condorcet The Rediscovery of Voting Theory [continued] Arrow n Relies on Black to understand Condorcet](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-48.jpg)
![The Rediscovery of Voting Theory [continued] Arrow n n n Unrestricted domain or universality The Rediscovery of Voting Theory [continued] Arrow n n n Unrestricted domain or universality](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-49.jpg)
![The Rediscovery of Voting Theory [continued] Brams and Fishburn n Develop formal proposal for The Rediscovery of Voting Theory [continued] Brams and Fishburn n Develop formal proposal for](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-50.jpg)
![The Rediscovery of Voting Theory [continued] Saari n Develops a geometric framework for comparing The Rediscovery of Voting Theory [continued] Saari n Develops a geometric framework for comparing](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-51.jpg)
![The Rediscovery of Voting Theory [continued] Preference Aggregation Issues n Vote trading and fungible The Rediscovery of Voting Theory [continued] Preference Aggregation Issues n Vote trading and fungible](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-52.jpg)
![The Rediscovery of Voting Theory [continued] Competence in Social Choice n Young: Maximum likelihood The Rediscovery of Voting Theory [continued] Competence in Social Choice n Young: Maximum likelihood](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-53.jpg)
![The Rediscovery of Voting Theory [continued] Grofman-Shapley Theorem n How to weight votes in The Rediscovery of Voting Theory [continued] Grofman-Shapley Theorem n How to weight votes in](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-54.jpg)

- Slides: 57

An Introduction to Voting Theory: History and Procedures Arnold B. Urken Professor of Political Science Division of Humanities and Social Science Stevens Institute of Technology aurken@stevens. edu DIMACS Workshop, May 10, 2004 © 2004. Arnold B. Urken All Rights Reserved 1

Outline n Top Six Voting Systems n Pre-18 th Century Voting Theory n 18 th Century France: The Golden Age? n The Rediscovery of Voting Theory n Preference Aggregation Issues n Competence in Voting Theory © 2004. Arnold B. Urken All Rights Reserved 2

Top Six Voting Systems n Plurality voting n Borda voting n Condorcet scoring n Copeland scoring n Approval voting n STV (IRV) © 2004. Arnold B. Urken All Rights Reserved 3
![Top Six Voting Systems continued Voting systems include rules for Vote Endowment number of Top Six Voting Systems [continued] Voting systems include rules for Vote Endowment: number of](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-4.jpg)
Top Six Voting Systems [continued] Voting systems include rules for Vote Endowment: number of votes used to express preferences Vote Allocation: Saving or trading? Vote Aggregation: Standard for producing a collective outcome. Allocation => “fungible voting, ” which allows votes to be saved and traded © 2004. Arnold B. Urken All Rights Reserved 4

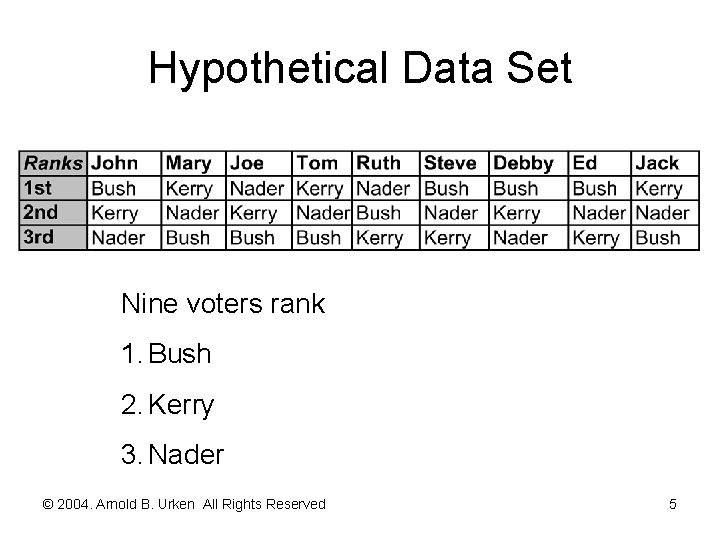
Hypothetical Data Set Nine voters rank 1. Bush 2. Kerry 3. Nader © 2004. Arnold B. Urken All Rights Reserved 5
![Top Six Voting Procedures continued Plurality Voting Endowment One vote for the most preferred Top Six Voting Procedures [continued] Plurality Voting Endowment: One vote for the most preferred](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-6.jpg)
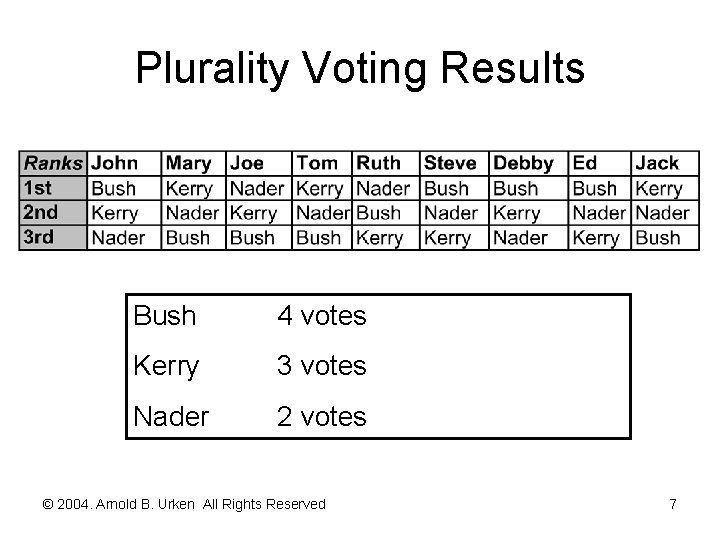
Top Six Voting Procedures [continued] Plurality Voting Endowment: One vote for the most preferred choice Allocation: Trading/saving not explicitly allowed Aggregation: Choice with the most votes wins (plurality) © 2004. Arnold B. Urken All Rights Reserved 6

Plurality Voting Results Bush 4 votes Kerry 3 votes Nader 2 votes © 2004. Arnold B. Urken All Rights Reserved 7

Plurality vs. Majority What’s the Difference? n Absolute vs. relative majority n Historically n Sanior et major pars n Right/healthy and greater part n Used to overturn outcomes n Sanior difficult to measure, so major used © 2004. Arnold B. Urken All Rights Reserved 8
![Top Six Voting Procedures continued Borda Voting Endowment Assign ranks to choices Allocation Tradingsaving Top Six Voting Procedures [continued] Borda Voting Endowment: Assign ranks to choices Allocation: Trading/saving](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-9.jpg)
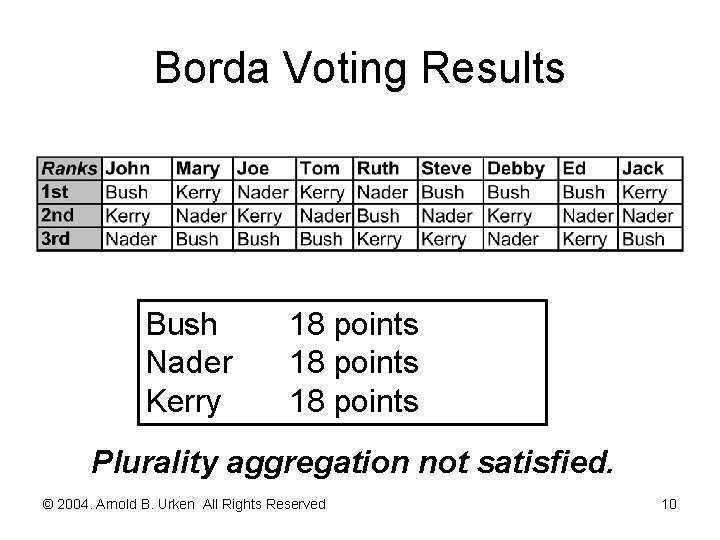
Top Six Voting Procedures [continued] Borda Voting Endowment: Assign ranks to choices Allocation: Trading/saving not explicitly allowed Aggregation: Choice with the most votes wins (plurality) © 2004. Arnold B. Urken All Rights Reserved 9

Borda Voting Results Bush Nader Kerry 18 points Plurality aggregation not satisfied. © 2004. Arnold B. Urken All Rights Reserved 10

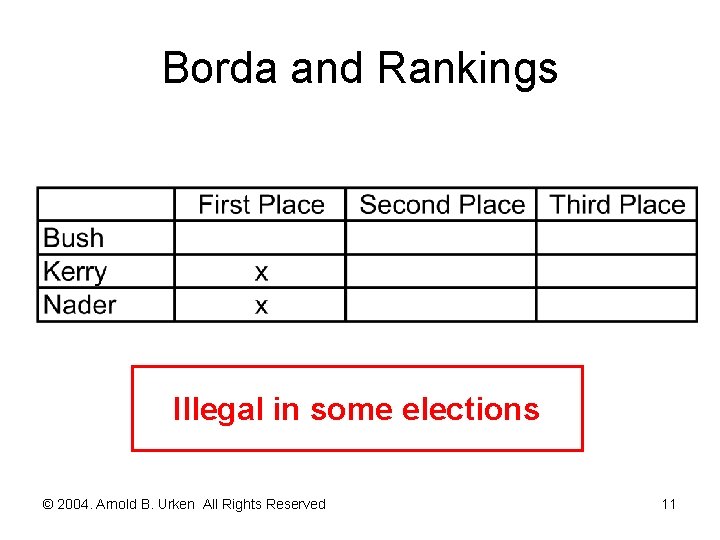
Borda and Rankings Illegal in some elections © 2004. Arnold B. Urken All Rights Reserved 11
![Borda and Rankings continued Not used this way 2004 Arnold B Urken All Borda and Rankings [continued] Not used this way © 2004. Arnold B. Urken All](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-12.jpg)
Borda and Rankings [continued] Not used this way © 2004. Arnold B. Urken All Rights Reserved 12
![Top Six Voting Procedures continued Condorcet Scoring Endowment Ordinal rankings assigned to choices Allocation Top Six Voting Procedures [continued] Condorcet Scoring Endowment: Ordinal rankings assigned to choices Allocation:](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-13.jpg)
Top Six Voting Procedures [continued] Condorcet Scoring Endowment: Ordinal rankings assigned to choices Allocation: Trading/saving not explicitly allowed Aggregation: Winner is the choice with the most victories in binary comparisons © 2004. Arnold B. Urken All Rights Reserved 13

Condorcet Scoring Results Bush Kerry Nader 9 points Plurality aggregation not satisfied. © 2004. Arnold B. Urken All Rights Reserved 14
![Top Seven Voting Procedures continued Copeland Scoring Endowment Ordinal rankings assigned to choices Allocation Top Seven Voting Procedures [continued] Copeland Scoring Endowment: Ordinal rankings assigned to choices Allocation:](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-15.jpg)
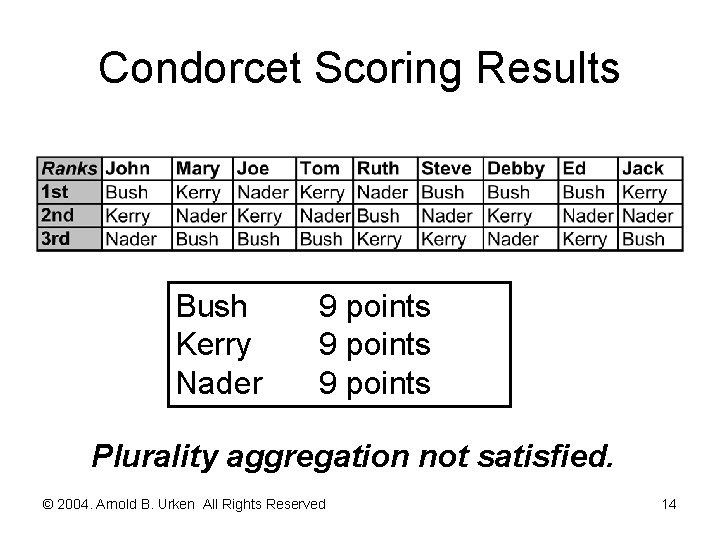
Top Seven Voting Procedures [continued] Copeland Scoring Endowment: Ordinal rankings assigned to choices Allocation: Trading/saving not explicitly allowed Aggregation: Winner is the choice with greatest net score in binary comparisons © 2004. Arnold B. Urken All Rights Reserved 15

Copeland Scoring Results Bush Nader Kerry 0 points Plurality aggregation not satisfied. © 2004. Arnold B. Urken All Rights Reserved 16
![Top Seven Voting Procedures continued Approval Voting Endowment N votes where N number Top Seven Voting Procedures [continued] Approval Voting Endowment: N votes where N = number](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-17.jpg)
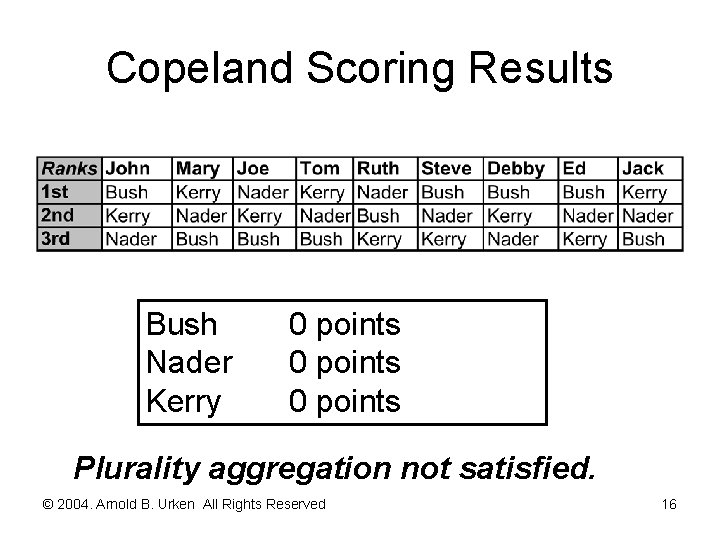
Top Seven Voting Procedures [continued] Approval Voting Endowment: N votes where N = number of choices Allocation: One vote cast for each approved choice; no trading/saving Aggregation: Plurality, majority, or unanimity © 2004. Arnold B. Urken All Rights Reserved 17

Approval Voting Results Assuming one approval vote is cast for 1 st and 2 nd place choices Bush Nader Kerry 5 points 6 points 5 points Nader is the plurality winner! Based on the number of voters who approve him © 2004. Arnold B. Urken All Rights Reserved 18
![Top Seven Voting Procedures continued Observations about Approval Voting n Empirical observation Voters cast Top Seven Voting Procedures [continued] Observations about Approval Voting n Empirical observation: Voters cast](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-19.jpg)
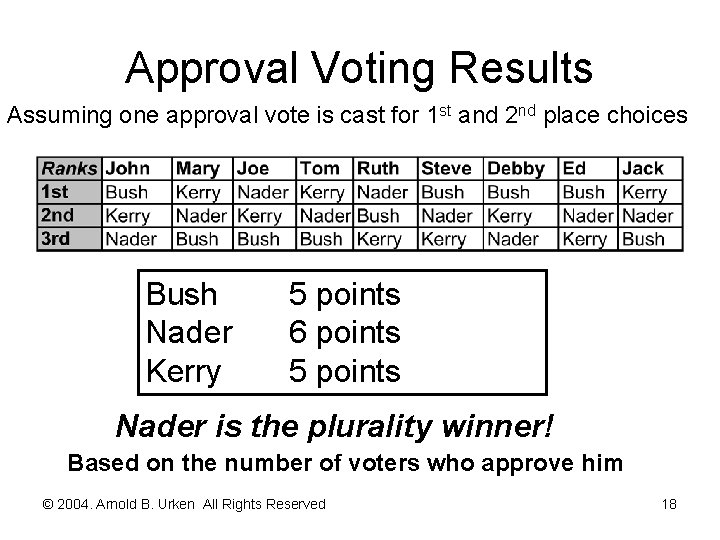
Top Seven Voting Procedures [continued] Observations about Approval Voting n Empirical observation: Voters cast an approval vote for each choice ≥ average utility n Ties possible under plurality, majority, and unanimous aggregation rules n Definitions of base for aggregation n All allocated votes n The number of voters casting votes © 2004. Arnold B. Urken All Rights Reserved 19
![Top Seven Voting Procedures continued STV IRVProportional Representation Endowment Assign ranks to choices Allocation Top Seven Voting Procedures [continued] STV (IRV--Proportional Representation) Endowment: Assign ranks to choices Allocation:](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-20.jpg)
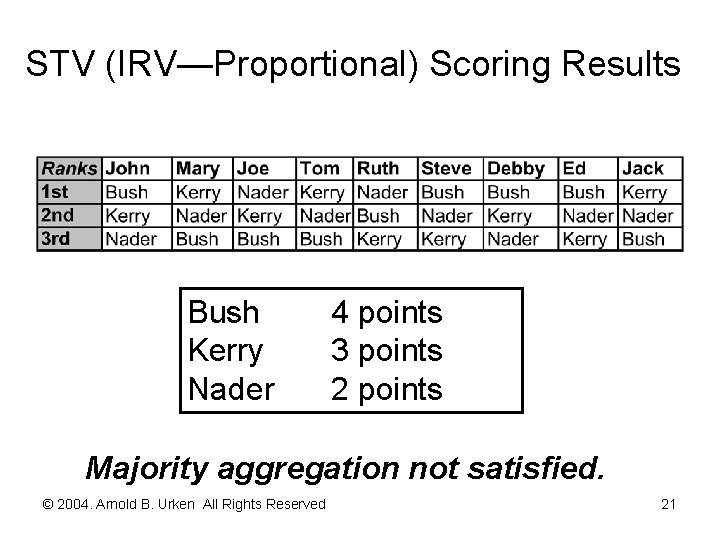
Top Seven Voting Procedures [continued] STV (IRV--Proportional Representation) Endowment: Assign ranks to choices Allocation: One choice for each rank, trading/saving: not explicitly allowed Aggregation: Majority of first place votes, but if no choice wins, eliminate the most choice most frequently ranked last and count first place preferences again until a majority winner is produced © 2004. Arnold B. Urken All Rights Reserved 20

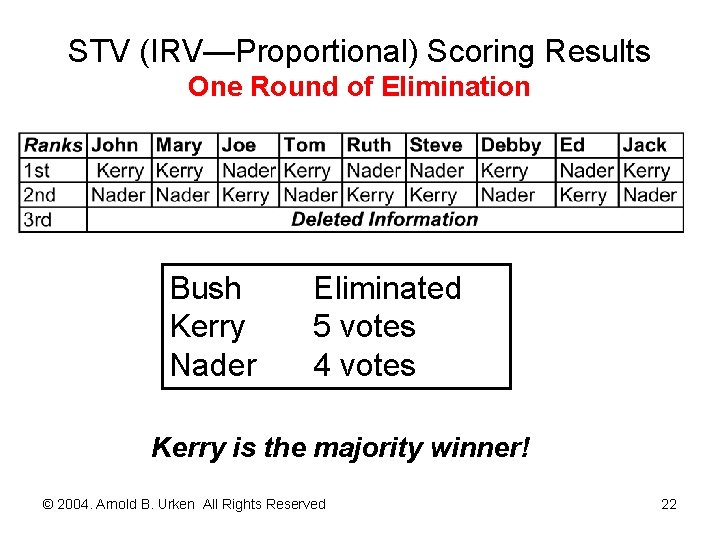
STV (IRV—Proportional) Scoring Results Bush Kerry Nader 4 points 3 points 2 points Majority aggregation not satisfied. © 2004. Arnold B. Urken All Rights Reserved 21

STV (IRV—Proportional) Scoring Results One Round of Elimination Bush Kerry Nader Eliminated 5 votes 4 votes Kerry is the majority winner! © 2004. Arnold B. Urken All Rights Reserved 22

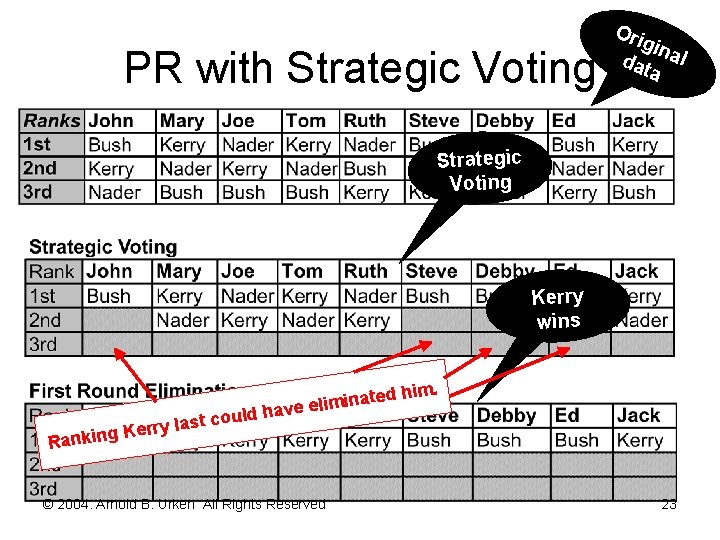
PR with Strategic Voting Ori gin dat al a Strategic Voting Kerry wins im. ated h n i m i l e ave R uld h o c t s a l erry anking K © 2004. Arnold B. Urken All Rights Reserved 23

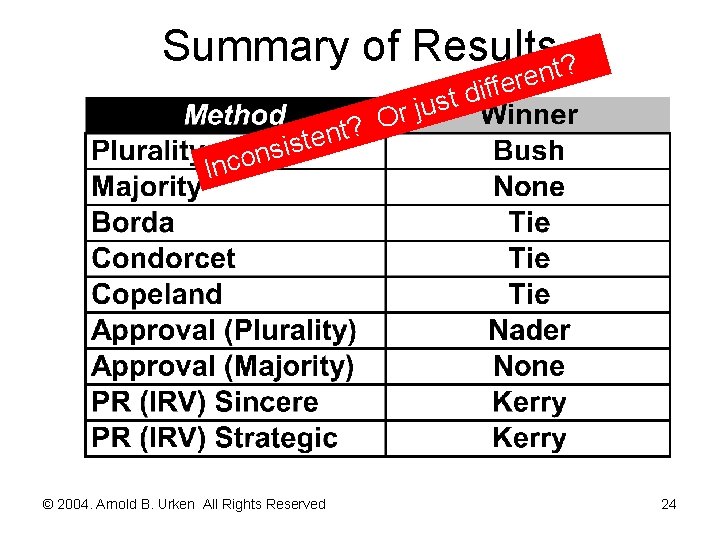
Summary of Resultsnt? t? n e t s i s n Inco © 2004. Arnold B. Urken All Rights Reserved re e f f i td s u j Or 24

Pre-18 th Century Voting Theory General Observations n Theoretical insights were derived from practical problem solving n Knowledge was not cumulative n The communication of votes was an issue “Science” was • “pre-normal” Kuhnian framework • early stage Popperian “metaphysical” research program © 2004. Arnold B. Urken All Rights Reserved 25
![Pre18 th Century Voting Theory continued n Pliny the Younger n Ramon Lull n Pre-18 th Century Voting Theory [continued] n Pliny the Younger n Ramon Lull n](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-26.jpg)
Pre-18 th Century Voting Theory [continued] n Pliny the Younger n Ramon Lull n Nicolaus Cusanus n The Venetian Mehod © 2004. Arnold B. Urken All Rights Reserved 26
![Pre18 th Century Voting Theory continued n Pliny the Younger n Letter to Titius Pre-18 th Century Voting Theory [continued] n Pliny the Younger n Letter to Titius](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-27.jpg)
Pre-18 th Century Voting Theory [continued] n Pliny the Younger n Letter to Titius Aristo, A. D. 105 n Agenda manipulation in the trial of Afranius Dexter’s slaves n Slaves accused of murdering his master n Options n Acquittal n Banishment n Death © 2004. Arnold B. Urken All Rights Reserved 27
![Pre18 th Century Voting Theory continued n Execution faction leader leads switch from death Pre-18 th Century Voting Theory [continued] n Execution faction leader leads switch from death](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-28.jpg)
Pre-18 th Century Voting Theory [continued] n Execution faction leader leads switch from death to banishment n Banishment is the majority choice n Pliny’s faction favored leniency, but included less than one-half of all votes © 2004. Arnold B. Urken All Rights Reserved 28
![Pre18 th Century Voting Theory continued n Pliny calls for ternary vote with division Pre-18 th Century Voting Theory [continued] n Pliny calls for ternary vote (with division](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-29.jpg)
Pre-18 th Century Voting Theory [continued] n Pliny calls for ternary vote (with division of the whole) n Pliny knew that the opposition had the following preference orders: Death > Banishment > Acquittal > Death © 2004. Arnold B. Urken All Rights Reserved 29
![Pre18 th Century Voting Theory continued n Why n Neither Acquittal nor Death would Pre-18 th Century Voting Theory [continued] n Why? n Neither Acquittal nor Death would](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-30.jpg)
Pre-18 th Century Voting Theory [continued] n Why? n Neither Acquittal nor Death would get a majority in the first round of voting—in binary comparisons n In the second round of voting, the winner of the first round of voting (Acquittal or Death) would lose to Banishment n Sincere and manipulated voting produce the same outcome! n Pliny uncomfortable: inconsistent with Senate customs? © 2004. Arnold B. Urken All Rights Reserved 30
![Pre18 th Century Voting Theory continued n Issues Raised n Sincere voting honest communication Pre-18 th Century Voting Theory [continued] n Issues Raised n Sincere voting: honest communication](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-31.jpg)
Pre-18 th Century Voting Theory [continued] n Issues Raised n Sincere voting: honest communication of preferences n Strategic voting: changing “sincere” votes to manipulate the collective outcome n Pliny anticipates Robin Farquharson, Theory of Voting. Yale, 1969 © 2004. Arnold B. Urken All Rights Reserved 31
![Pre18 th Century Voting Theory continued Ramon Lull A D 1232 1316 n Explored Pre-18 th Century Voting Theory [continued] Ramon Lull A. D. 1232 -1316 n Explored](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-32.jpg)
Pre-18 th Century Voting Theory [continued] Ramon Lull A. D. 1232 -1316 n Explored methods for honest church elections n Two methods based on selections of pairs of choices from a larger set of ranked choices n Blanquera (1285) n De Arte Eleccionis (1299) © 2004. Arnold B. Urken All Rights Reserved 32
![Pre18 th Century Voting Theory continued Blanquerna 1285 n Mixed method art Borda and Pre-18 th Century Voting Theory [continued] Blanquerna (1285) n Mixed method (“art”) Borda and](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-33.jpg)
Pre-18 th Century Voting Theory [continued] Blanquerna (1285) n Mixed method (“art”) Borda and Condorcet n Electors choose Blanquerna as bishop without following the “art” they generate an indecisive outcome and the decision must be appealed to the Pope to produce a winner n Work reflects ambivalence about preference aggregation and making the right choice. © 2004. Arnold B. Urken All Rights Reserved 33
![Pre18 th Century Voting Theory continued De Arte Eleccionis 1299 n Condorcet scoring n Pre-18 th Century Voting Theory [continued] De Arte Eleccionis (1299) n Condorcet scoring n](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-34.jpg)
Pre-18 th Century Voting Theory [continued] De Arte Eleccionis (1299) n Condorcet scoring n Uses matrix notation (next used by Dodgson in the 19 th century) n Method does not address collective intransitivity (later discovered by Condorcet and Arrow) © 2004. Arnold B. Urken All Rights Reserved 34
![Pre18 th Century Voting Theory continued Nicolaus Cusanus 1430 n Goal design an honest Pre-18 th Century Voting Theory [continued] Nicolaus Cusanus (1430) n Goal: design an “honest”](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-35.jpg)
Pre-18 th Century Voting Theory [continued] Nicolaus Cusanus (1430) n Goal: design an “honest” voting procedure to elect a Holy Roman Emperor to end a long schism in the papacy n Proposes a Borda system n n Applies it to propositions with more than two choices Criticizes manipulation of electorsand criticizes attempts to control the collective outcome by manipulating electors. n Implicitly suggests that voting by ballot is new © 2004. Arnold B. Urken All Rights Reserved 35
![Pre18 th Century Voting Theory continued The Venetian Method 13 th Century n Similar Pre-18 th Century Voting Theory [continued] The Venetian Method (13 th Century) n Similar](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-36.jpg)
Pre-18 th Century Voting Theory [continued] The Venetian Method (13 th Century) n Similar to approval voting n Simplified the process of selecting 41 electors from an initial assembly of 1500 members. © 2004. Arnold B. Urken All Rights Reserved 36

18 th Century France: The Golden Age? n Voting in the French Academy of Sciences n Borda, Condorcet, and others n Condorcet and the French Revolution n Daunou and after n Proportional voting © 2004. Arnold B. Urken All Rights Reserved 37
![18 th Century France The Golden Age continued Voting in the French Academy of 18 th Century France: The Golden Age? [continued] Voting in the French Academy of](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-38.jpg)
18 th Century France: The Golden Age? [continued] Voting in the French Academy of Sciences n Scientists recommend top three candidates to the King of France n Plurality voting used since 1699, ties rare. n 1770 Borda talk about plurality voting n Borda paper not published until 1784 © 2004. Arnold B. Urken All Rights Reserved 38
![18 th Century France The Golden Age continued Voting in the French Academy of 18 th Century France: The Golden Age? [continued] Voting in the French Academy of](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-39.jpg)
18 th Century France: The Golden Age? [continued] Voting in the French Academy of Sciences n Borda and Condorcet were political enemies n Borda fought in the American Revolution n Condorcet, a modernist, won a manipulated election as Secretary © 2004. Arnold B. Urken All Rights Reserved 39
![18 th Century France The Golden Age continued Voting in the French Academy of 18 th Century France: The Golden Age? [continued] Voting in the French Academy of](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-40.jpg)
18 th Century France: The Golden Age? [continued] Voting in the French Academy of Sciences n No evidence of actual voting debate n Condorcet regards Borda’s work as physicaille (petty experiments) n Condorcet’s 1785 Essai sur l’application d’analyse à probabilité des décisions rendues à la pluralité des voix © 2004. Arnold B. Urken All Rights Reserved 40
![18 th Century France The Golden Age continued Voting in the French Academy of 18 th Century France: The Golden Age? [continued] Voting in the French Academy of](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-41.jpg)
18 th Century France: The Golden Age? [continued] Voting in the French Academy of Sciences n The 1785 Essai n Goal: analyze the probability of making a correct collective choice n Introduction: identifies collective intransitivity n Body: 13 hypothetical situations © 2004. Arnold B. Urken All Rights Reserved 41

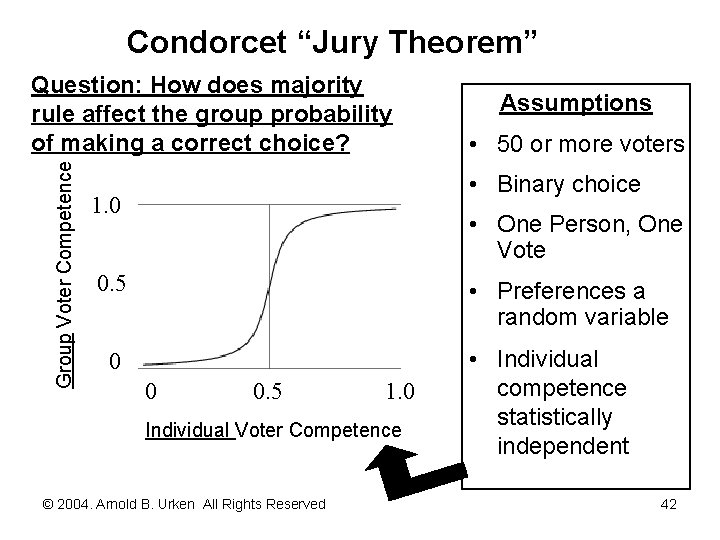
Condorcet “Jury Theorem” Group Voter Competence Question: How does majority rule affect the group probability of making a correct choice? Assumptions • 50 or more voters • Binary choice 1. 0 • One Person, One Vote 0. 5 • Preferences a random variable 0 0 0. 5 1. 0 Individual Voter Competence © 2004. Arnold B. Urken All Rights Reserved • Individual competence statistically independent 42
![18 th Century France The Golden Age continued Condorcet and the French Revolution n 18 th Century France: The Golden Age? [continued] Condorcet and the French Revolution n](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-43.jpg)
18 th Century France: The Golden Age? [continued] Condorcet and the French Revolution n Creates practical voting plan for the Republican Constitution with binary agendas n Recommends jury design for the trial of the King of France n Robespierre’s hit list drives him underground n Dies in prison? © 2004. Arnold B. Urken All Rights Reserved 43
![18 th Century France The Golden Age continued Daunou and after n FAS becomes 18 th Century France: The Golden Age? [continued] Daunou and after n FAS becomes](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-44.jpg)
18 th Century France: The Golden Age? [continued] Daunou and after n FAS becomes the Institute of France n New election method needed n Napoléon interested n Borda and Daunou on commission n Daunou writes critique of Borda voting © 2004. Arnold B. Urken All Rights Reserved 44
![18 th Century France The Golden Age continued Daunou and after continued n Voting 18 th Century France: The Golden Age? [continued] Daunou and after (continued) n Voting](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-45.jpg)
18 th Century France: The Golden Age? [continued] Daunou and after (continued) n Voting theory is lost in French probability theory (Cf. Daston) n Ideas rediscovered by Dodgson (Lewis Carroll) n Nanson (Australia) refers to Condorcet’s ideas in designing elections for scientists © 2004. Arnold B. Urken All Rights Reserved 45
![18 th Century France The Golden Age continued Daunou and after continued n Proportional 18 th Century France: The Golden Age? [continued] Daunou and after (continued) n Proportional](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-46.jpg)
18 th Century France: The Golden Age? [continued] Daunou and after (continued) n Proportional voting developed for allocating seats in legislatures n Ideas are not integrated with voting theorists © 2004. Arnold B. Urken All Rights Reserved 46

The Rediscovery of Voting Theory Black n Does archival research on Condorcet n Coins “jury theorem” to explain Condorcet’s interest in competence n Develops “single-peakedness” concept to explain collective intransitivity © 2004. Arnold B. Urken All Rights Reserved 47
![The Rediscovery of Voting Theory continued Arrow n Relies on Black to understand Condorcet The Rediscovery of Voting Theory [continued] Arrow n Relies on Black to understand Condorcet](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-48.jpg)
The Rediscovery of Voting Theory [continued] Arrow n Relies on Black to understand Condorcet n Invents the term “social choice” n Axiomatizes collective intransitivity problem in impossibility theorem © 2004. Arnold B. Urken All Rights Reserved 48
![The Rediscovery of Voting Theory continued Arrow n n n Unrestricted domain or universality The Rediscovery of Voting Theory [continued] Arrow n n n Unrestricted domain or universality](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-49.jpg)
The Rediscovery of Voting Theory [continued] Arrow n n n Unrestricted domain or universality Non-imposition or citizen sovereignty Non-dictatorship Monotonicity Independence of irrelevant alternatives Impossible to satisfy all conditions simultaneously © 2004. Arnold B. Urken All Rights Reserved 49
![The Rediscovery of Voting Theory continued Brams and Fishburn n Develop formal proposal for The Rediscovery of Voting Theory [continued] Brams and Fishburn n Develop formal proposal for](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-50.jpg)
The Rediscovery of Voting Theory [continued] Brams and Fishburn n Develop formal proposal for approval voting n Scientific societies adopt approval voting n Articulate theoretical and empirical arguments © 2004. Arnold B. Urken All Rights Reserved 50
![The Rediscovery of Voting Theory continued Saari n Develops a geometric framework for comparing The Rediscovery of Voting Theory [continued] Saari n Develops a geometric framework for comparing](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-51.jpg)
The Rediscovery of Voting Theory [continued] Saari n Develops a geometric framework for comparing voting methods for three choices n Does not address n Ties n Truncated preferences n Competence © 2004. Arnold B. Urken All Rights Reserved 51
![The Rediscovery of Voting Theory continued Preference Aggregation Issues n Vote trading and fungible The Rediscovery of Voting Theory [continued] Preference Aggregation Issues n Vote trading and fungible](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-52.jpg)
The Rediscovery of Voting Theory [continued] Preference Aggregation Issues n Vote trading and fungible voting n Manipulation: potential vs. actual n Voter use of voting methods n Ranking choices (STV) n Identifying approved set of choices © 2004. Arnold B. Urken All Rights Reserved 52
![The Rediscovery of Voting Theory continued Competence in Social Choice n Young Maximum likelihood The Rediscovery of Voting Theory [continued] Competence in Social Choice n Young: Maximum likelihood](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-53.jpg)
The Rediscovery of Voting Theory [continued] Competence in Social Choice n Young: Maximum likelihood interpretation of Condorcet’s rule n Grofman (Owen, Feld) n Explore models of competence n Show that Condorcet solved Rousseau’s problem of reconciling “general will” and the “will of all” © 2004. Arnold B. Urken All Rights Reserved 53
![The Rediscovery of Voting Theory continued GrofmanShapley Theorem n How to weight votes in The Rediscovery of Voting Theory [continued] Grofman-Shapley Theorem n How to weight votes in](https://slidetodoc.com/presentation_image_h/7496436546b60fad290fceac5318ca4d/image-54.jpg)
The Rediscovery of Voting Theory [continued] Grofman-Shapley Theorem n How to weight votes in interdependent collective decisions n Don’t weight votes by using the ratio of p/1 -p (ratio of competence to incompetence) n Instead use ln p/1 -p Experimental Confirmation © 2004. Arnold B. Urken All Rights Reserved 54

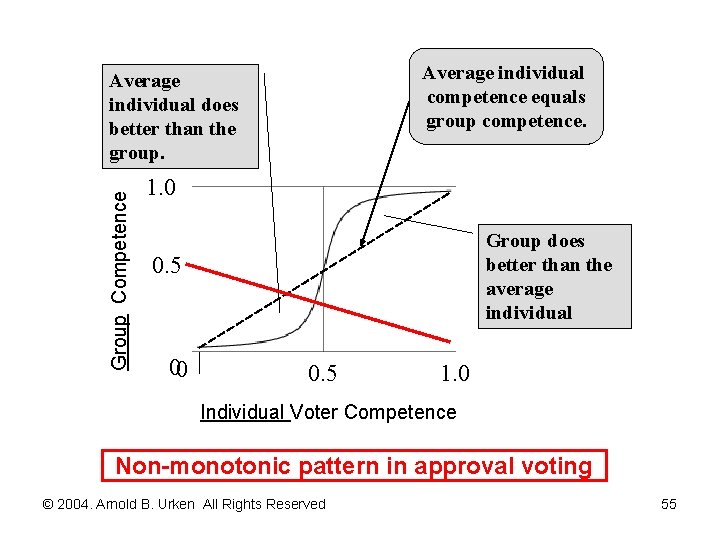
Average individual competence equals group competence. Group Competence Average individual does better than the group. 1. 0 Group does better than the average individual 0. 5 00 0. 5 1. 0 Individual Voter Competence Non-monotonic pattern in approval voting © 2004. Arnold B. Urken All Rights Reserved 55

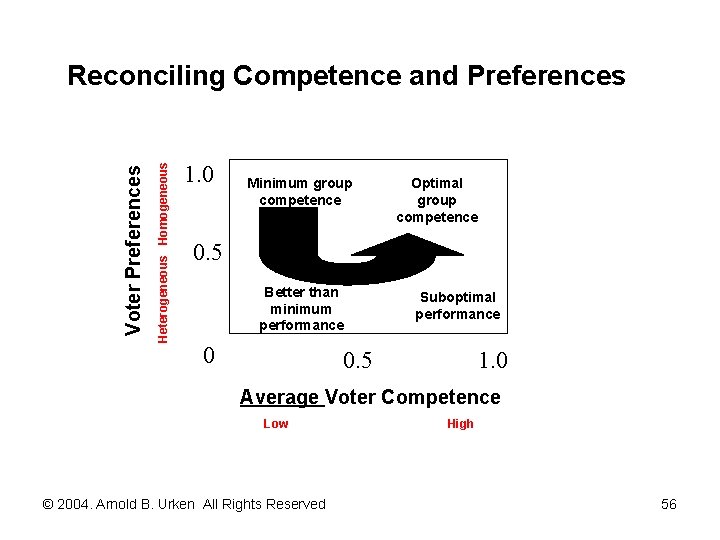
Heterogeneous Homogeneous Voter Preferences Reconciling Competence and Preferences 1. 0 Minimum group competence Optimal group competence 0. 5 Better than minimum performance 0 Suboptimal performance 0. 5 1. 0 Average Voter Competence Low © 2004. Arnold B. Urken All Rights Reserved High 56

Perspective n History not of purely antiquarian interest n Draws our attention to models and problems of integrating ideas n Unresolved dualism n Preference aggregation n Competence © 2004. Arnold B. Urken All Rights Reserved 57