An Introduction to the Finite Element Analysis Presented

An Introduction to the Finite Element Analysis Presented by G. Velmurugan ME

Agenda PART I Introduction and Basic Concepts 1. 0 Computational Methods 1. 1 1. 2 1. 3 2. 0 The Finite Elements Method 2. 1 2. 2 3. 0 Idealization Discretization Solution FEM Notation Element Types Mechanichal Approach 3. 1 3. 2 3. 3 3. 4 The Problem Setup Strain Energy External Energy The Potential Energy Functional Joint Advanced Student School St. Petersburg 2005

Agenda PART II Mathematical Formulation 4. 0 The Mathematics Behind the Method 4. 1 4. 2 4. 3 4. 4 4. 5 4. 6 4. 7 4. 8 Weighted Residual Methods Approxiamting Functions The Residual Galerkin’s Method The Weak Form Solution Space Linear System of Equations Connection to the physical system Joint Advanced Student School St. Petersburg 2005

Agenda PART III Finite Element Discretization 5. 0 Finite Element Discretization 4. 1 4. 2 4. 3 4. 4 4. 5 4. 6 4. 7 6. 0 7. 0 The Trial Basis Matrix Form of the Problem Element Stiffness Matrix Element Mass Matrix External Work Integral Assembling Linear System of Equations References Question and Answers Joint Advanced Student School St. Petersburg 2005

PART I Introduction and Basic Concepts

1. 0 Computational Methods Joint Advanced Student School St. Petersburg 2005

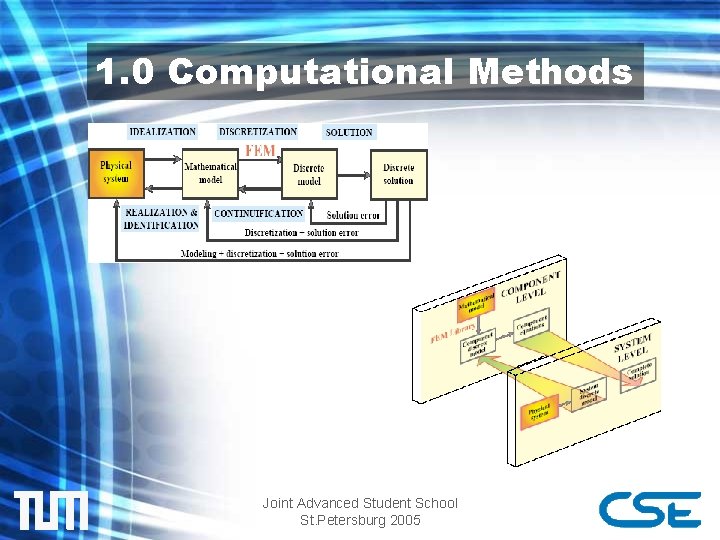
1. 1 Idealization • Mathematical Models • “A model is a symbolic device built to simulate and predict aspects of behavior of a system. ” • Abstraction of physical reality • Implicit vs. Explicit Modelling • Implicit modelling consists of using existent pieces of abstraction and fitting them into the particular situation (e. g. Using general purpose FEM programs) • Explicit modelling consists of building the model from scratch Joint Advanced Student School St. Petersburg 2005

1. 2 Dicretization 1. Finite Difference Discretization • • • The solution is discretized Stability Problems Loss of physical meaning 2. Finite Element Discretization • • • The problem is discretized Physical meaning is conserved on elements Interpretation and Control is easier Joint Advanced Student School St. Petersburg 2005

1. 3 Solution 1. Linear System Solution Algorithms • • • Gaussian Elimination Fast Fourier Transform Relaxation Techniques 2. Error Estimation and Convergence Analysis Joint Advanced Student School St. Petersburg 2005

2. 0 Finite Element Method • Two interpretations 1. Physical Interpretation: The continous physical model is divided into finite pieces called elements and laws of nature applied on the generic element. The results are then recombined to represent the continuum. 2. Mathematical Interpretation: The differetional equation reppresenting the system is converted into a variational form, which is approximated by the linear combination of a finite set of trial functions. Joint Advanced Student School St. Petersburg 2005

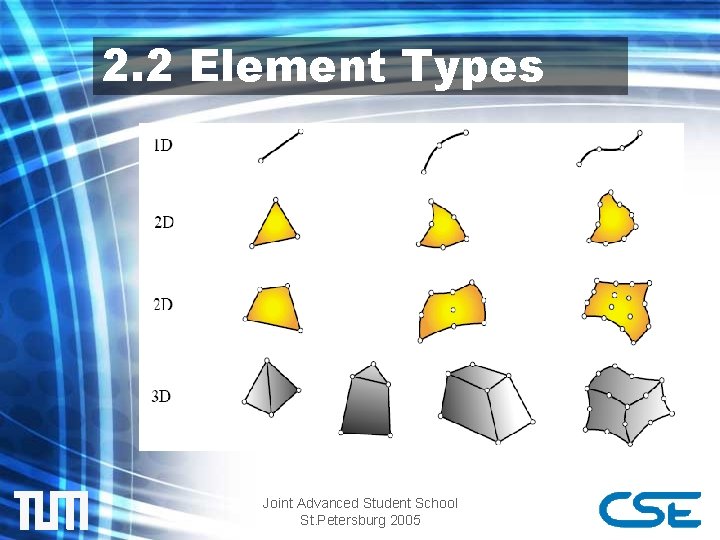
2. 1 FEM Notation Elements are defined by the following properties: 1. Dimensionality 2. Nodal Points 3. Geometry 4. Degrees of Freedom 5. Nodal Forces (Non homogeneous RHS of the DE) Joint Advanced Student School St. Petersburg 2005

2. 2 Element Types Joint Advanced Student School St. Petersburg 2005

3. 0 Mechanical Approach • • Simple mechanical problem Introduction of basic mechanical concepts Introduction of governing equations Mechanical concepts used in mathematical derivation Joint Advanced Student School St. Petersburg 2005

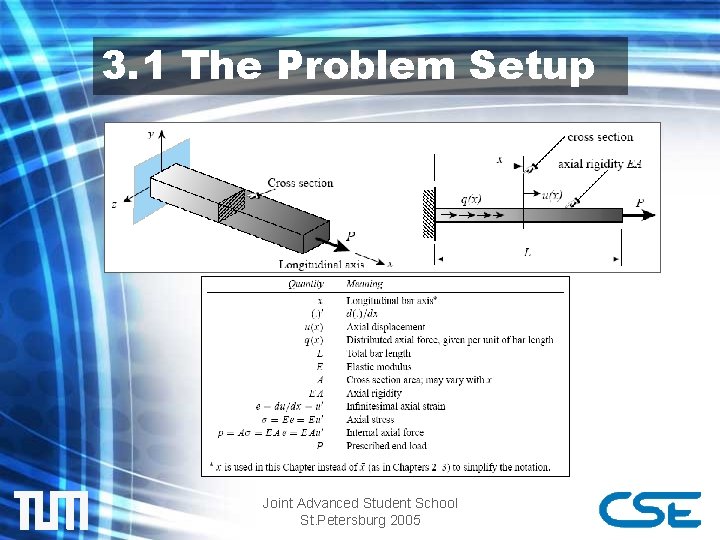
3. 1 The Problem Setup Joint Advanced Student School St. Petersburg 2005

3. 2 Strain Energy • Hooke’s Law: where • Strain Energy Density: Joint Advanced Student School St. Petersburg 2005

3. 2 Strain Energy (cont’d) • Integrating over the Volume of the Bar: • All quantities may depend on x. Joint Advanced Student School St. Petersburg 2005

3. 3 External Energy • Due to applied external loads 1. The distributed load q(x) 2. The point end load P. This can be included in q. • External Energy: Joint Advanced Student School St. Petersburg 2005

3. 4 The Total Potential Energy Functional • The unknown strain Function u is found by minimizing the TPE functional described below: Joint Advanced Student School St. Petersburg 2005

PART II Mathematical Formulation

4. 0 Historical Background • Hrennikof and Mc. Henry formulated a 2 D structural problem as an assembly of bars and beams • Courant used a variational formulation to approximate PDE’s by linear interpolation over triangular elements • Turner wrote a seminal paper on how to solve one and two dimensional problems using structural elements or triangular and rectangular elements of continuum. Joint Advanced Student School St. Petersburg 2005

4. 1 Weighted Residual Methods The class of differential equations containing also the one dimensional bar described above can be described as follows : Joint Advanced Student School St. Petersburg 2005

4. 1 Weighted Residual Methods It follows that: Multiplying this by a weight function v and integrating over the whole domain we obtain: For the inner product to exist v must be “square integrable” Therefore: Equation (2) is called variational form Joint Advanced Student School St. Petersburg 2005

4. 2 Approximating Function • We can replace u and v in the formula with their approximation function i. e. • The functions fj and yj are of our choice and are meant to be suitable to the particular problem. For example the choice of sine and cosine functions satisfy boundary conditions hence it could be a good choice. Joint Advanced Student School St. Petersburg 2005

4. 2 Approximating Function • U is called trial function and V is called test function • As the differential operator L[u] is second order • Therefore we can see U as element of a finite-diemnsional subspace of the infinite-dimensional function space C 2(0, 1) • The same way Joint Advanced Student School St. Petersburg 2005

4. 3 The Residual • Replacing v and u with respectively V and U (2) becomes • • r(x) is called the residual (as the name of the method suggests) The vanishing inner product shows that the residual is orthogonal to all functions V in the test space. Joint Advanced Student School St. Petersburg 2005

4. 3 The Residual • Substituting into and exchanging summations and integrals we obtain • As the inner product equation is satisfied for all choices of V in SN the above equation has to be valid for all choices of dj which implies that Joint Advanced Student School St. Petersburg 2005

4. 4 Galerkin’s Method • One obvious choice of would be taking it equal to • This Choice leads to the Galerkin’s Method • This form of the problem is called the strong form of the problem. Because the so chosen test space has more continuity than necessary. • Therefore it is worthwile for this and other reasons to convert the problem into a more symmetrical form • This can be acheived by integrating by parts the initial strong form of the problem. Joint Advanced Student School St. Petersburg 2005

4. 5 The Weak Form • Let us remember the initial form of the problem • Integrating by parts Joint Advanced Student School St. Petersburg 2005

4. 5 The Weak Form • The problem can be rewritten as where • The integration by parts eliminated the second derivatives from the problem making it possible less continouity than the previous form. This is why this form is called weak form of the problem. • A(v, u) is called Strain Energy. Joint Advanced Student School St. Petersburg 2005

4. 6 Solution Space • Now that derivative of v comes into the picture v needs to have more continoutiy than those in L 2. As we want to keep symmetry its appropriate to choose functions that produce bounded values of • As p and z are necessarily smooth functions the following restriction is sufficient • Functions obeying this rule belong to the so called Sobolev Space and they are denoted by H 1. We require v and u to satisfy boundary conditions so we denote the resulting space as Joint Advanced Student School St. Petersburg 2005

4. 7 Linear System of Equations • The solution now takes the form • Substituting the approximate solutions obtained earlier in the more general WRM we obtain • More explicitly substituting U and V (remember we chose them to have the same base) and swapping summations and integrals we obtain Joint Advanced Student School St. Petersburg 2005

4. 8 Connection to the Physical System Mechanical Formulation Mathematical Formulation Joint Advanced Student School St. Petersburg 2005

PART III Finite Element Discretization

5. 0 Finite Element Discretization • Let us take the initial value problem with constant coefficients • As a first step let us divide the domain in N subintervals with the following mesh • Each subinterval is called Joint Advanced Student School St. Petersburg 2005 finite element.

5. 1 The Trial Basis • Next we select as a basis the so called “hat function”. Joint Advanced Student School St. Petersburg 2005

5. 1 The Trial Basis • With the basis in the previous slide we construct our approximate solution U(x) • It is interesting to note that the coefficients correspond to the values of U at the interior nodes Joint Advanced Student School St. Petersburg 2005

5. 1 The Trial Basis • The problem at this point can be easily solved using the previously derived Galerkin’s Method • A little more work is needed to convert this problem into matrix notation Joint Advanced Student School St. Petersburg 2005

5. 2 Matrix Form of the Problem • Restricting U over the typical finite element we can write • Which in turn can be written as in the same way Joint Advanced Student School St. Petersburg 2005

5. 2 Matrix Form of the Problem • Taking the derivative • Derivative of V is analogus Joint Advanced Student School St. Petersburg 2005

5. 2 Matrix Form of the Problem • The variational formula can be elementwise defined as follows: Joint Advanced Student School St. Petersburg 2005

4. 3 The Element Stiffnes Matrix • Substituting U, V, U’ and V’ into these formulae we obtain Joint Advanced Student School St. Petersburg 2005

4. 4 The Element Mass Matrix • The same way Joint Advanced Student School St. Petersburg 2005

4. 5 External Work Integral • The external work integral cannot be evaluated for every function q(x) • We can consider a linear interpolant of q(x) for simplicity. • Substituting and evaluating the integral Element load vector Joint Advanced Student School St. Petersburg 2005

4. 6 Assembling • Now the task is to assemble the elements into the whole system in fact we have to sum each integral over all the elements • For doing so we can extend the dimension of each element matrix to N and then put the 2 x 2 matrix at the appropriate position inside it • With all matrices and vectors having the same dimension the summation looks like Joint Advanced Student School St. Petersburg 2005

4. 6 Assembling • Doing the same for the Mass Matrix and for the Load Vector Joint Advanced Student School St. Petersburg 2005

4. 7 Linear System of Equations • Substituting this Matrix form of the expressions in we obtain the following set of linear equations • This has to be satisfied for all choices of d therefore Joint Advanced Student School St. Petersburg 2005

References • Carlos Felippa http: //caswww. colorado. edu/courses. d/IFEM. d/IFE M. Ch 06. d/IFEM. Ch 06. pdf • Joseph E Flaherty, Amos Eaton Professor http: //www. cs. rpi. edu/~flaherje/FEM/fem 1. ps • Gilbert Strang, George J. Fix An Analysis of the Finite Element Method Prentice-Hall, 1973 Joint Advanced Student School St. Petersburg 2005