An Introduction to Support Vector Machine SVM Classification

An Introduction to Support Vector Machine (SVM)

Classification l Everyday, all the time we classify things. l Eg crossing the street: ¡Is there a car coming? ¡At what speed? ¡How far is it to the other side? ¡Classification: Safe to walk or not!!!

Classification Formulation l Given ¡an input space ¡a set of classes ={ } l the Classification Problem is ¡to define a mapping f: g where each x in is assigned to one class l This mapping function is called a Decision Function

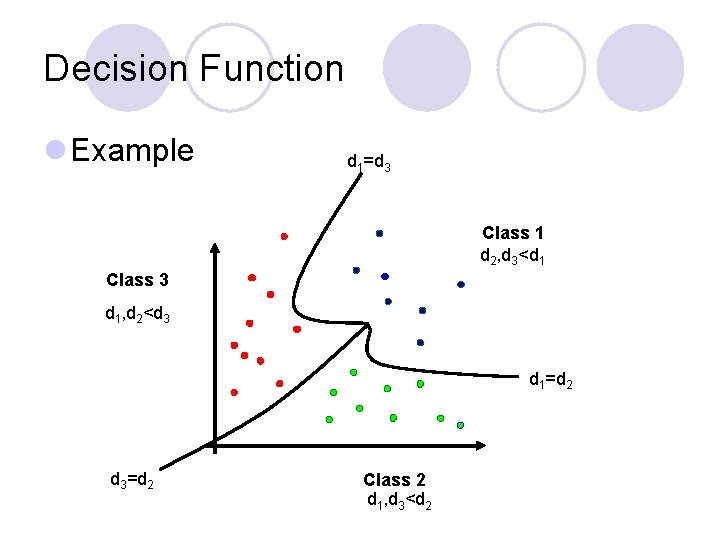
Decision Function l Example d 1=d 3 Class 1 d 2, d 3<d 1 Class 3 d 1, d 2<d 3 d 1=d 2 d 3=d 2 Class 2 d 1, d 3<d 2

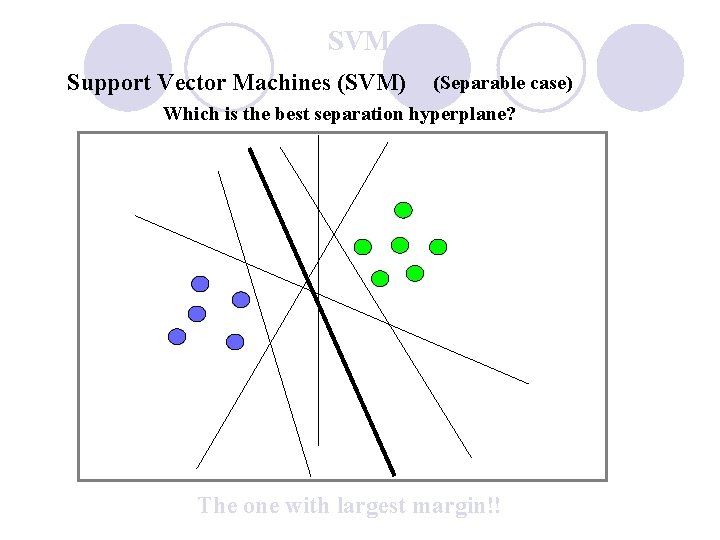
SVM Support Vector Machines (SVM) (Separable case) Which is the best separation hyperplane? The one with largest margin!!

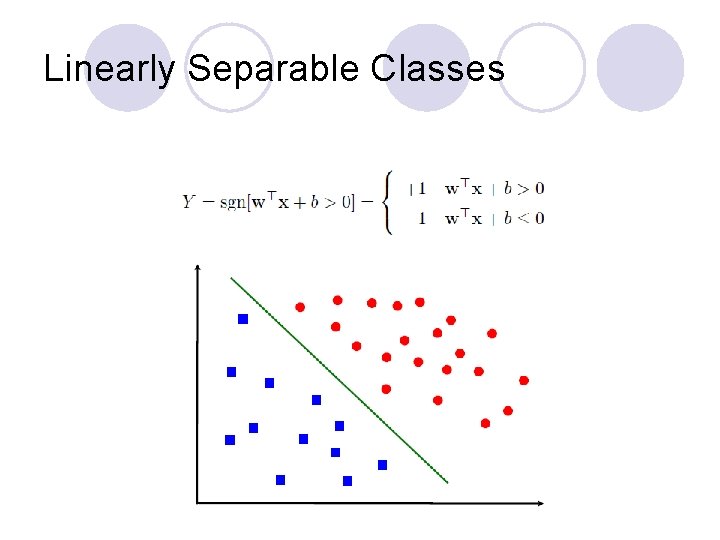
Linearly Separable Classes

Support Vector Machines (SVM) large margin provides better generalization ability Maximizing Margin: Correct Separation:

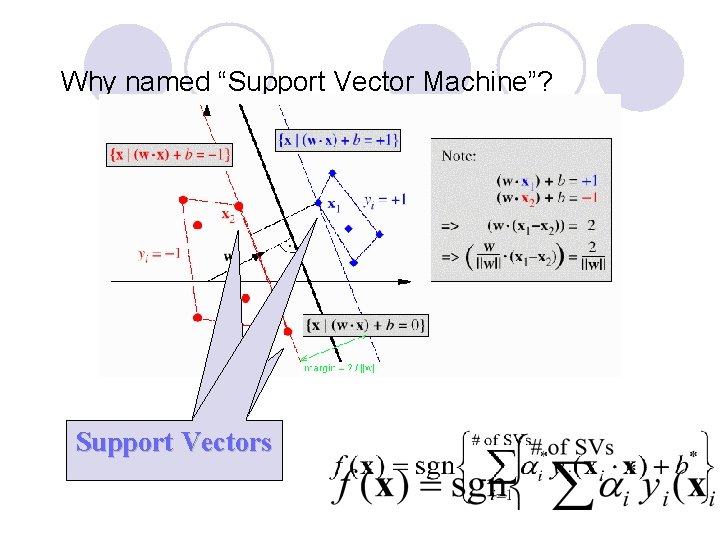
Why named “Support Vector Machine”? Support Vectors

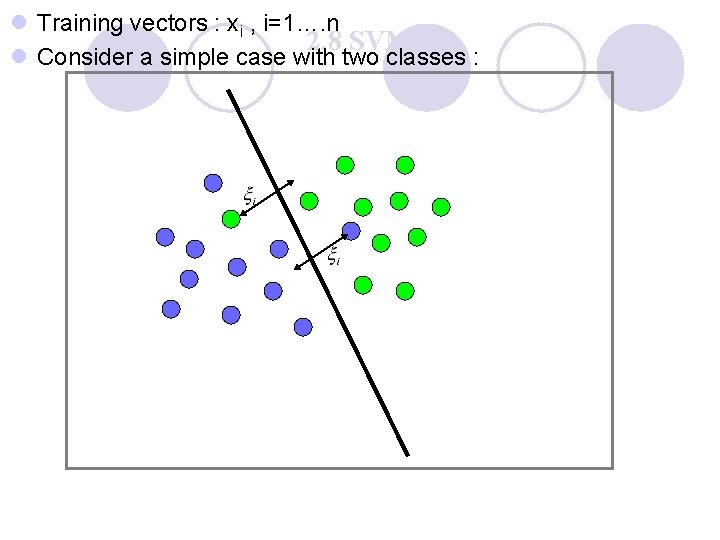
l Training vectors : xi , i=1…. n 2. 8 SVM l Consider a simple case with two classes :

Example l Suppose we are given the following positively labeled data points l (3, 1), (3, − 1), (6, − 1) l and the following negatively labeled data points l (1, 0), (0, 1), (0, − 1), (− 1, 0)

l We will use the supports as (1, 0) is -1, (3, 1) is +1 and (3, -1) is +1

Linear Separable SVM l Label the training data l Suppose we have some hyperplanes which separates the “+” from “-” examples (a separating hyperplane) l x which lie on the hyperplane, satisfy l w is noraml to hyperplane, |b|/||w|| is the perpendicular distance from hyperplane to origin

Linear Separable SVM l Define two support hyperplane as H 1: w. Tx = b +δ and H 2: w. Tx = b –δ l To solve over-parameterized problem, set δ=1 l Define the distance as l Margin = distance between H 1 and H 2 = 2/||w||

The Primal problem of SVM l Goal: Find a separating hyperplane with largest margin. A SVM is to find w and b that satisfy (1) minimize ||w||/2 = w. Tw/2 (2) yi(xi·w+b)-1 ≥ 0

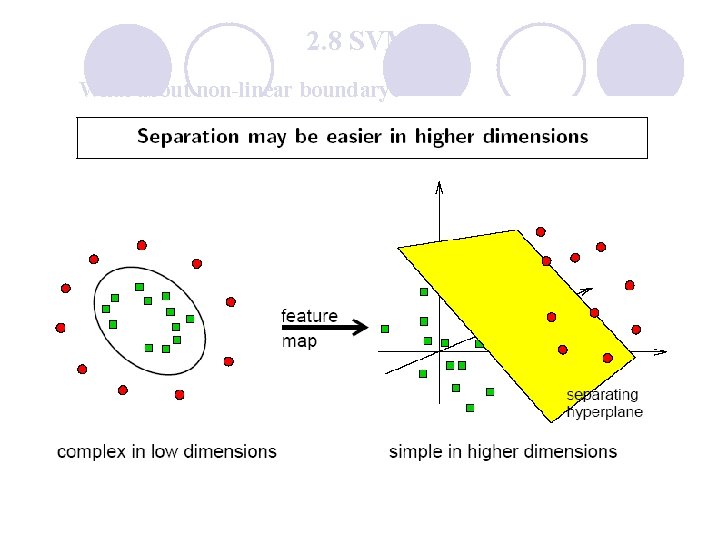
2. 8 SVM What about non-linear boundary?

Non-Linear Separable SVM : Kernal l To extend to non-linear case, we need to the data to some other Euclidean space.

Kernal l Φ is a mapping function. l Since the training algorithm only depend on data thru dot products. We can use a “kernal function” K such that l One commonly used example is radial based function (RBF)

Kernal l A RBF is a real-valued function whose value depends only on the distance from the origin, so that Φ(x)= Φ(||x||) ; or alternatively on the distance from some other point c, called a center, so that Φ(x, c)= Φ(||x-c||).

Non-separable SVM l Real world application usually have no OSH. We need to add an error term ζ. => l To give penalty to error term, define l New Lagrangian form is