An Introduction to Structured Output Learning Using Support

An Introduction to Structured Output Learning Using Support Vector Machines Yisong Yue Cornell University Some material used courtesy of Thorsten Joachims (Cornell University)

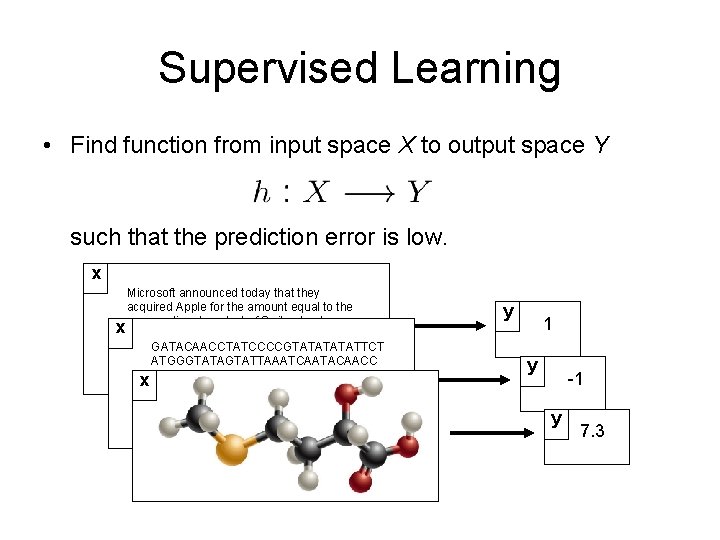
Supervised Learning • Find function from input space X to output space Y such that the prediction error is low. x Microsoft announced today that they acquired Apple for the amount equal to the national product of Switzerland. x gross Microsoft officials stated that they first GATACAACCTATCCCCGTATATTCT wanted to buy Switzerland, but eventually ATGGGTATAGTATTAAATCAATACAACC were turned off by the mountains and the snowy winters… x TATCCCCGTATATTCTATGGGTATA GTATTAAATCAATACAACCTATCCCCGT ATATTCTATGGGTATAGTATTAAAT CAGATACAACCTATCCCCGTATAT TCTATGGGTATAGTATTAAATCACATTTA y 1 y -1 y 7. 3

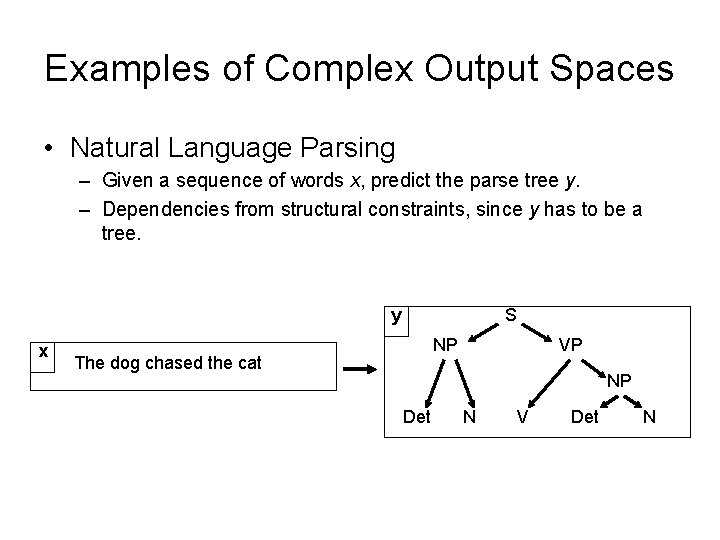
Examples of Complex Output Spaces • Natural Language Parsing – Given a sequence of words x, predict the parse tree y. – Dependencies from structural constraints, since y has to be a tree. y x S NP The dog chased the cat VP NP Det N V Det N

Examples of Complex Output Spaces • Part-of-Speech Tagging – Given a sequence of words x, predict sequence of tags y. – Dependencies from tag-tag transitions in Markov model. x The rain wet the cat y Det N V Det Similarly for other sequence labeling problems, e. g. , RNA Intron/Exon Tagging. N

Examples of Complex Output Spaces • Multi-class Labeling • Protein Sequence Alignment • Noun Phrase Co-reference Clustering • Learning Parameters of Graphical Models – Markov Random Fields • Multivariate Performance Measures – – F 1 Score ROC Area Average Precision NDCG

Notation • Bold x, y are structured input/output examples. – Usually consists of a collection of elements • x = (x 1, …, xn), y = (y 1, …, yn) – Each input element xi belongs to some high dimensional feature space, Rd – Each output element yi is usually a multiclass label or real valued number • Joint feature functions Ψ, Φ map input/output examples to points in RD

1 st Order Sequence Labeling • Given: – scoring function S(x, y 1, y 2) – input example (x 1, …, xn) • Finds sequence (y 1, …, yn) to maximize • Solved with dynamic programming (Viterbi)

Some Formulation Restrictions • Assume S is parameterized linearly by some weight vector w in RD. • This means that “Hypothesis Function”

The Linear Discriminant • From last slide: • Putting it together: • Our hypothesis function: “Linear Discriminant Function”

Structured Learning Problem • Efficient Inference/Prediction – hypothesis function solves for y when given x and w – – Viterbi in sequence labeling CKY Parser for parse trees Belief Propagation for Markov random fields Sorting for ranking • Efficient Learning/Training – need to efficiently learn parameters w from training data {xi, yi}i=1. . N – Solution: use Structural SVM framework – Can also use Perceptrons, CRFs, MEMMs, M 3 Ns etc.

How to Train? • Given a set of structured training examples {x(i), y(i)}i=1. . N • Different training methods can be used. – Perceptrons perform update whenever current model mispredicts. – CRFs plug the discriminant into a conditional log-likelihood function to optimize. – Structural SVMs solve a quadratic program minimizes a tradeoff between model complexity and a convex upper bound of performance loss.

Support Vector Machines • Input examples denoted by x (high dimensional point) • Output targets denoted by y (either +1 or -1) • SVMs learns a hyperplane w, predictions are sign(w. Tx) • Training involves finding w which minimizes • subject to • The sum of slacks upper bounds the accuracy loss

Structural SVM Formulation • Let x denote a structured input example (x 1, …, xn) • Let y denote a structured output target (y 1, …, yn) • Same objective function: • Constraints are defined for each incorrect labeling y’ over input x(i). • Discriminant score for the correct labeling at least as large as incorrect labeling plus the performance loss. • Another interpretation: the margin between correct label and incorrect label at least as large as how ‘bad’ the incorrect label is.

Adapting to Sequence Labeling • Minimize subject to Use the same slack variable for all constraints of the same structured training example where and • Sum of slacks upper bound performance loss. • Too many constraints!

Structural SVM Training • Suppose we only solve the SVM objective over a small subset of constraints (working set). • Some constraints from global set might be violated. • When finding a violated constraint, only y’ is free, everything else is fixed – y’s and x’s fixed from training – w and slack variables fixed from solving SVM objective • Degree of violation of a constraint is measured by:

Structural SVM Training • STEP 1: Solve the SVM objective function using only the current working set of constraints. • STEP 2: Using the model learned in STEP 1, find the most violated constraint from the global set of constraints. • STEP 3: If the constraint returned in STEP 2 is violated by more than epsilon, add it to the working set. • Repeat STEP 1 -3 until no additional constraints are added. Return the most recent model that was trained in STEP 1 -3 is guaranteed to loop for at most O(1/epsilon^2) iterations. [Tsochantaridis et al. 2005] *This is known as a “cutting plane” method.

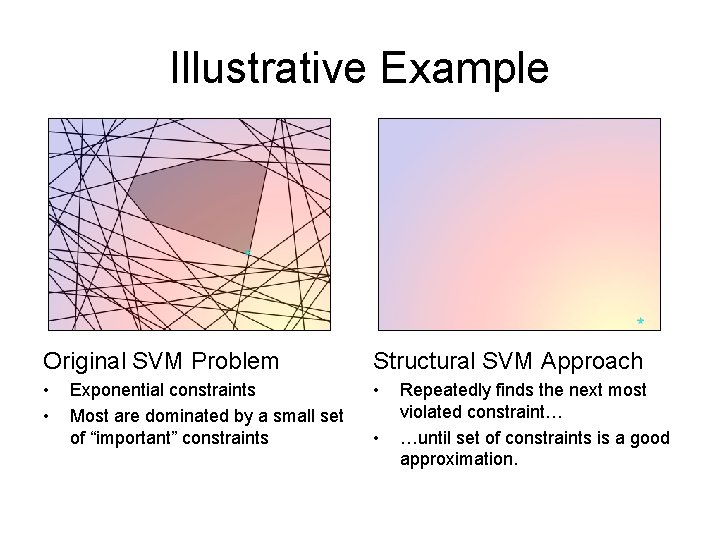
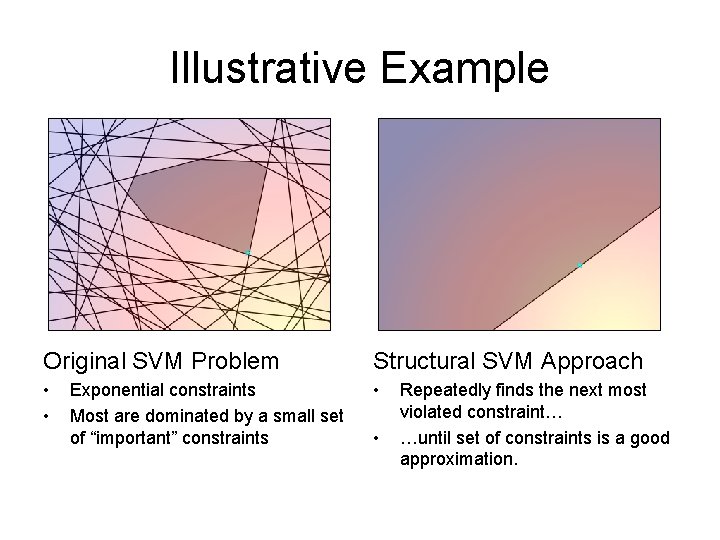
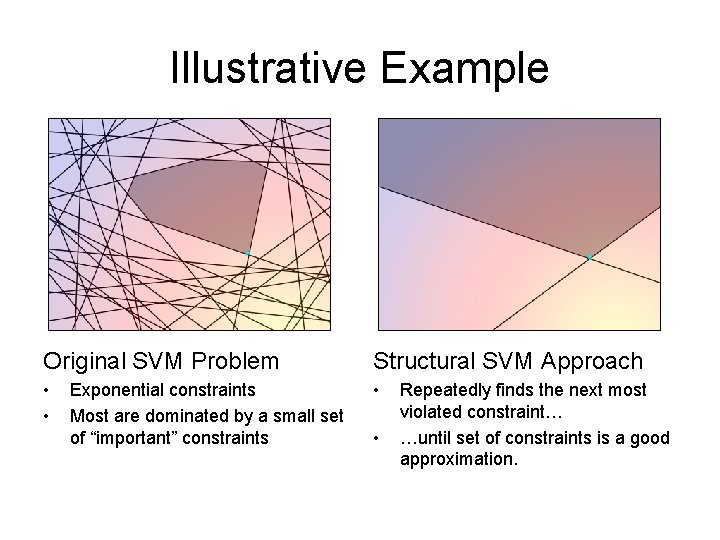
Illustrative Example Original SVM Problem Structural SVM Approach • • • Exponential constraints Most are dominated by a small set of “important” constraints • Repeatedly finds the next most violated constraint… …until set of constraints is a good approximation.

Illustrative Example Original SVM Problem Structural SVM Approach • • • Exponential constraints Most are dominated by a small set of “important” constraints • Repeatedly finds the next most violated constraint… …until set of constraints is a good approximation.

Illustrative Example Original SVM Problem Structural SVM Approach • • • Exponential constraints Most are dominated by a small set of “important” constraints • Repeatedly finds the next most violated constraint… …until set of constraints is a good approximation.

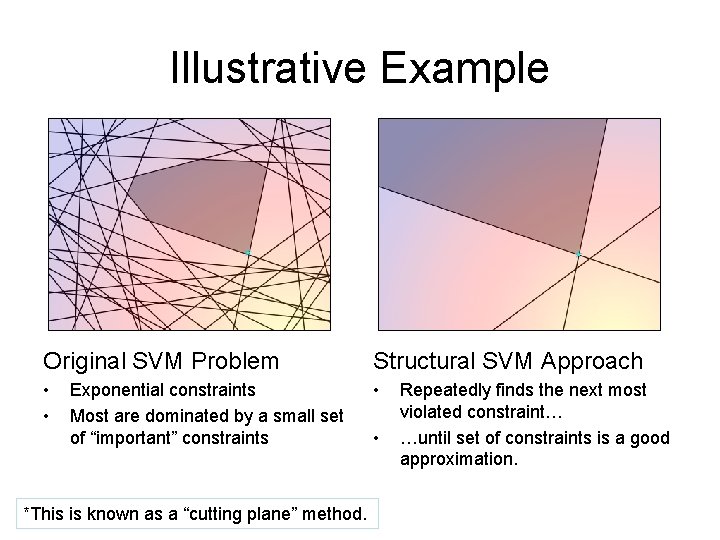
Illustrative Example Original SVM Problem Structural SVM Approach • • • Exponential constraints Most are dominated by a small set of “important” constraints *This is known as a “cutting plane” method. • Repeatedly finds the next most violated constraint… …until set of constraints is a good approximation.

Finding Most Violated Constraint • Structural SVM is an oracle framework. • Requires subroutine to find the most violated constraint. – Dependent on formulation of loss function and joint feature representation. • Exponential number of constraints! • Can usually expect efficient solution when inference has efficient algorithm.

Finding Most Violated Constraint • Finding most violated constraint is equivalent to maximizing the RHS w/o slack: • Requires solving: • Highly related to inference:

Sequence Labeling Revisited • Finding most violated constraint… … can be solved using Viterbi!

SVMStruct Abstracts Away “Structure” • Minimize: • Subject to: • Working set of constraints are fixed y’s and x’s: • Just like solving a conventional linear SVM! • Notion of “structure” almost completely used in finding the most violated constraint • (this is just an interpretation)