An Introduction to Graphene Electronic Structure Michael S

An Introduction to Graphene Electronic Structure Michael S. Fuhrer Department of Physics and Center for Nanophysics and Advanced Materials University of Maryland Michael S. Fuhrer University of Maryland

If you re-use any material in this presentation, please credit: Michael S. Fuhrer, University of Maryland Michael S. Fuhrer University of Maryland

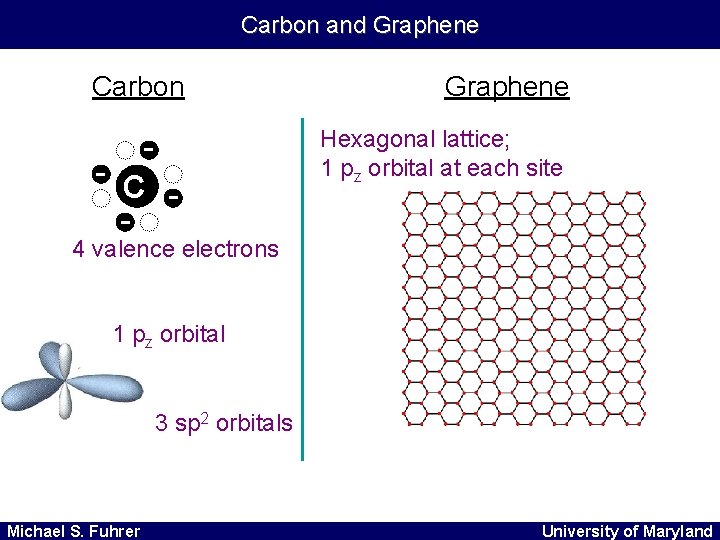
Carbon and Graphene Carbon Graphene - C - Hexagonal lattice; 1 pz orbital at each site 4 valence electrons 1 pz orbital 3 sp 2 orbitals Michael S. Fuhrer University of Maryland

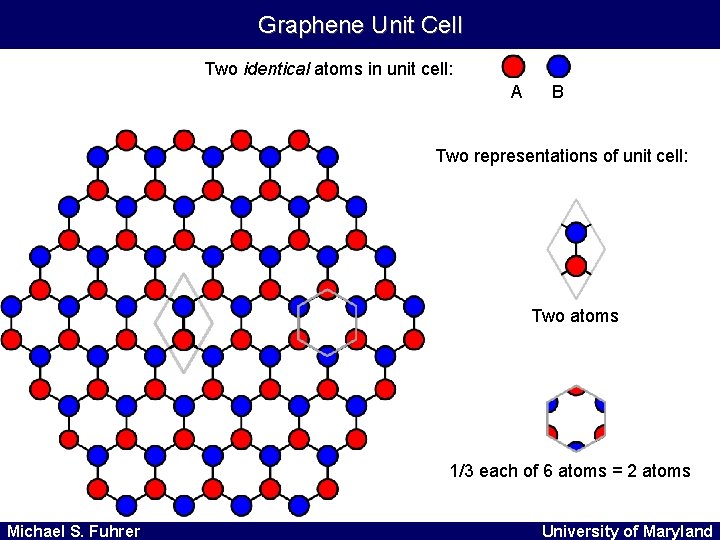
Graphene Unit Cell Two identical atoms in unit cell: A B Two representations of unit cell: Two atoms 1/3 each of 6 atoms = 2 atoms Michael S. Fuhrer University of Maryland

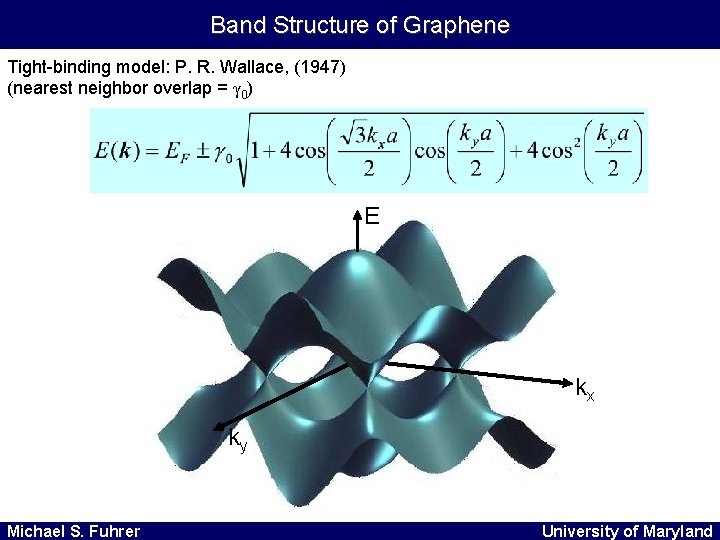
Band Structure of Graphene Tight-binding model: P. R. Wallace, (1947) (nearest neighbor overlap = γ 0) E kx ky Michael S. Fuhrer University of Maryland

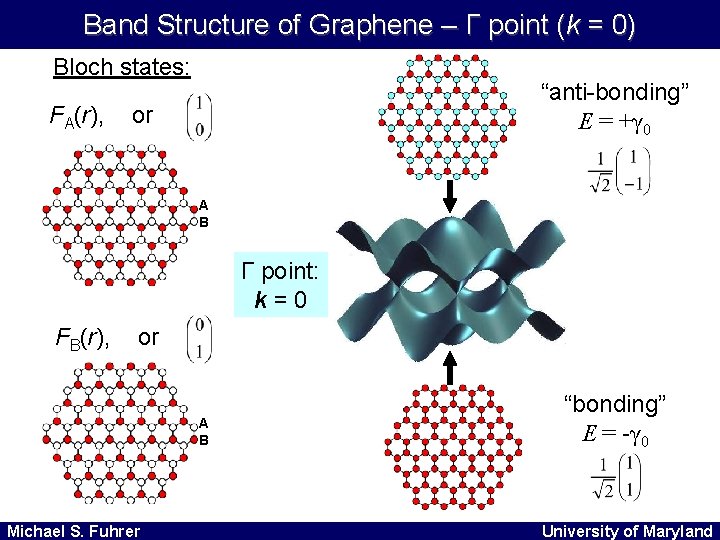
Band Structure of Graphene – Γ point (k = 0) Bloch states: FA(r), “anti-bonding” E = +γ 0 or A B Γ point: k=0 FB(r), or A B Michael S. Fuhrer “bonding” E = -γ 0 University of Maryland

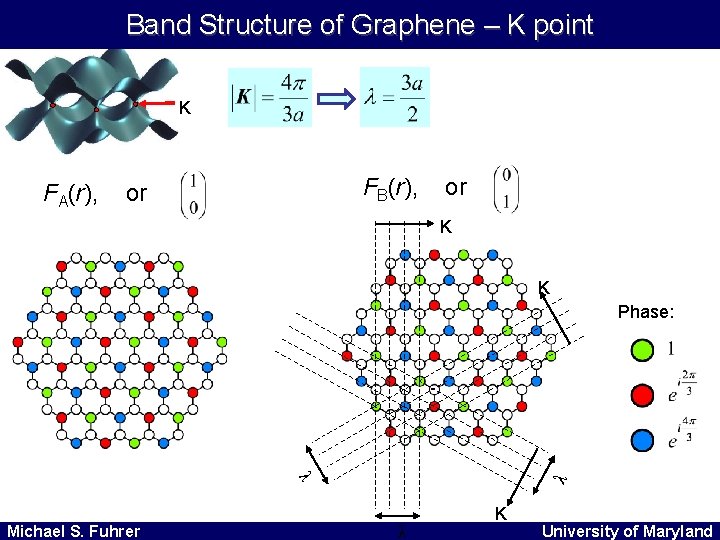
Band Structure of Graphene – K point K FA(r), FB(r), or or K K Phase: λ λ Michael S. Fuhrer λ K University of Maryland

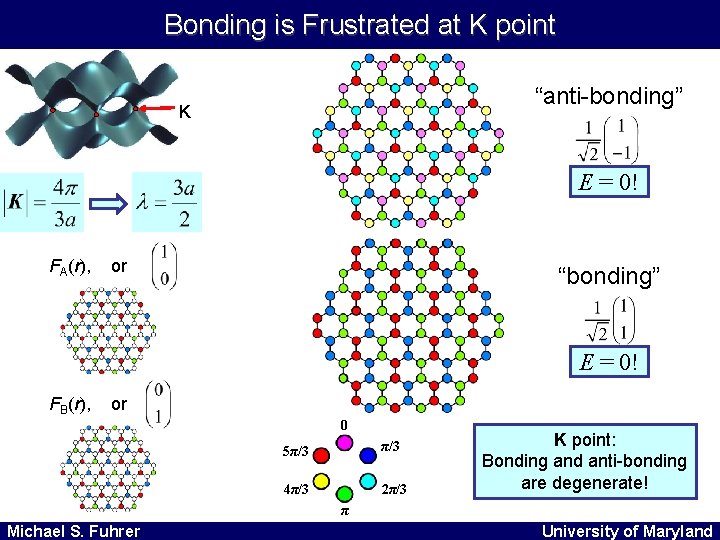
Bonding is Frustrated at K point “anti-bonding” K E = 0! FA(r), or “bonding” E = 0! FB(r), or 0 5π/3 4π/3 2π/3 K point: Bonding and anti-bonding are degenerate! π Michael S. Fuhrer University of Maryland

Band Structure of Graphene: k·p approximation Hamiltonian: K K’ Eigenvectors: θk is angle k makes with y-axis b = 1 for electrons, -1 for holes electron has “pseudospin” points. S. parallel Michael Fuhrer (anti-parallel) to momentum Energy: linear dispersion relation “massless” electrons University of Maryland

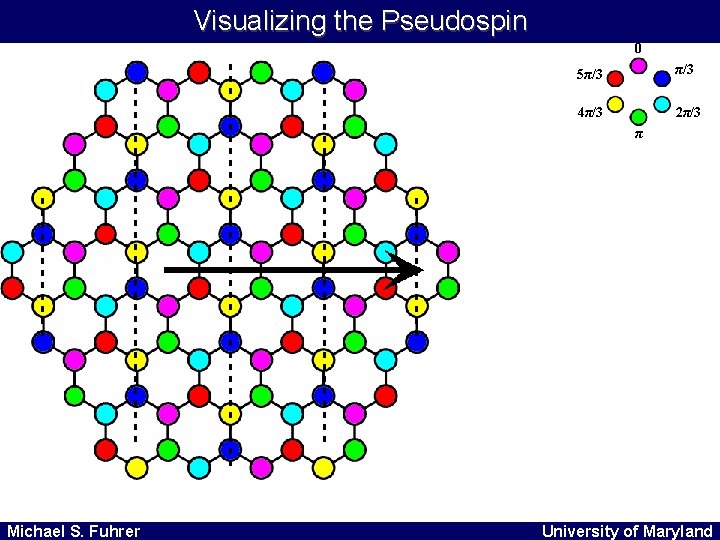
Visualizing the Pseudospin 0 5π/3 4π/3 2π/3 π Michael S. Fuhrer University of Maryland

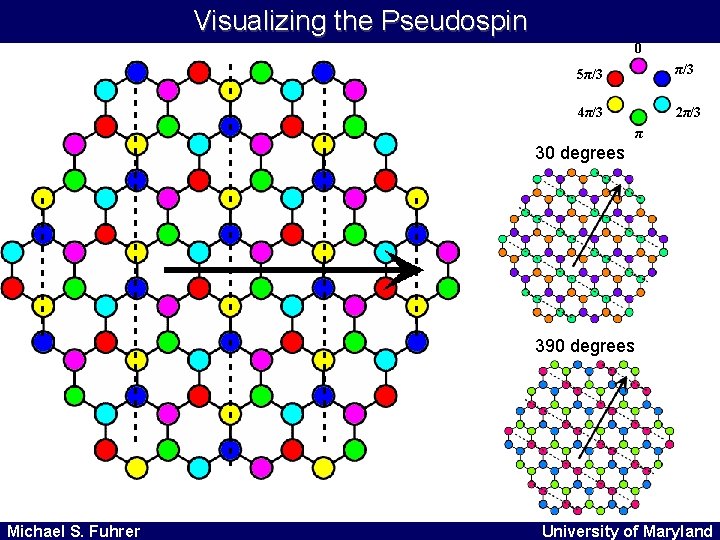
Visualizing the Pseudospin 0 5π/3 4π/3 2π/3 π 30 degrees 390 degrees Michael S. Fuhrer University of Maryland

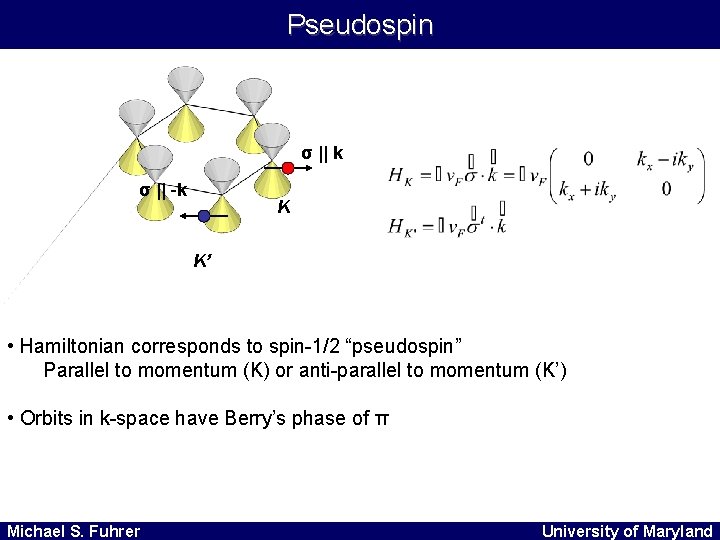
Pseudospin σ || k σ || -k K K’ • Hamiltonian corresponds to spin-1/2 “pseudospin” Parallel to momentum (K) or anti-parallel to momentum (K’) • Orbits in k-space have Berry’s phase of π Michael S. Fuhrer University of Maryland

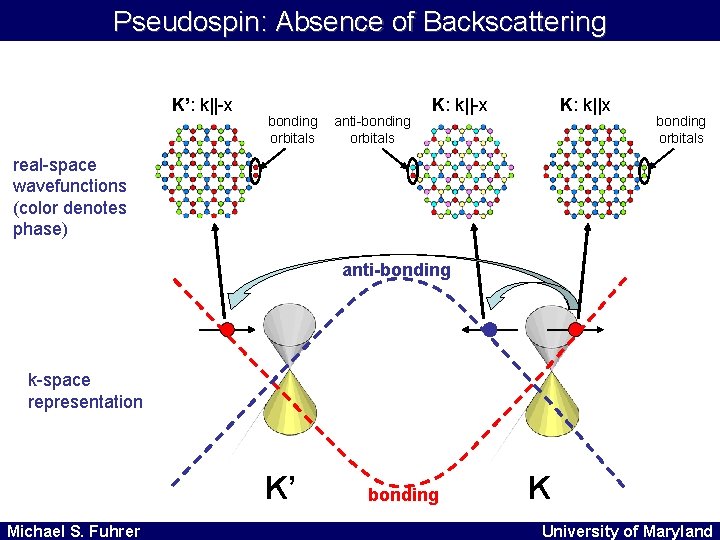
Pseudospin: Absence of Backscattering K’: k||-x bonding orbitals anti-bonding orbitals K: k||-x K: k||x bonding orbitals real-space wavefunctions (color denotes phase) anti-bonding k-space representation K’ Michael S. Fuhrer bonding K University of Maryland

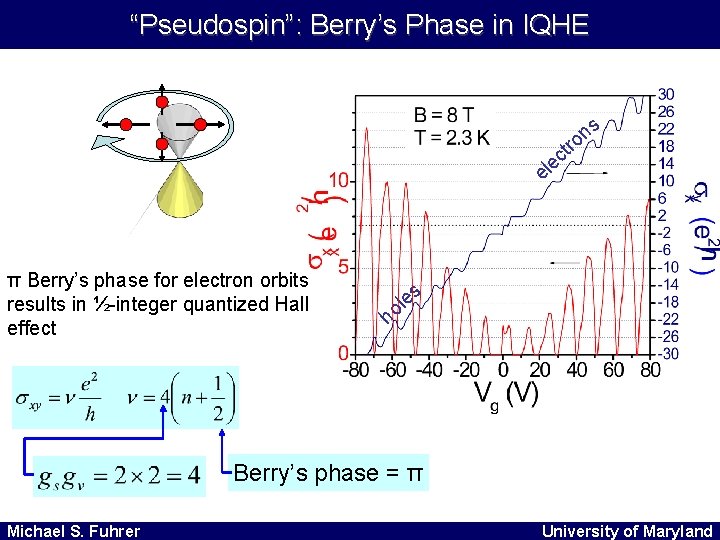
“Pseudospin”: Berry’s Phase in IQHE s n rt o c e el π Berry’s phase for electron orbits results in ½-integer quantized Hall effect es l o h Berry’s phase = π Michael S. Fuhrer University of Maryland

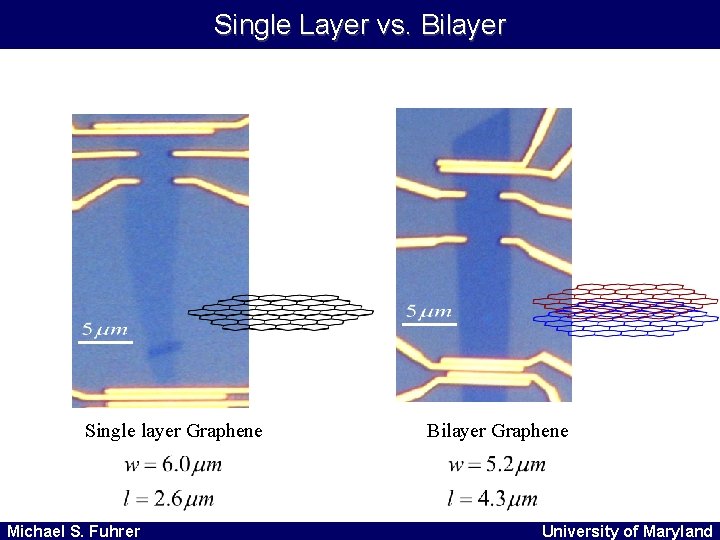
Graphene : Single vs. Bilayer Single Layer layer vs. Bilayer Single layer Graphene Michael S. Fuhrer Bilayer Graphene University of Maryland

Graphene Dispersion Relation: “Light-like” Bilayer Dispersion Relation: “Massive” E E ky ky kx kx Massive particles: Light: Electrons in graphene: Fermi velocity v. F instead of c v. F = 1 x 106 m/s ~ c/300 Michael S. Fuhrer Electrons in bilayer graphene: Effective mass m* instead of me m* = 0. 033 me University of Maryland

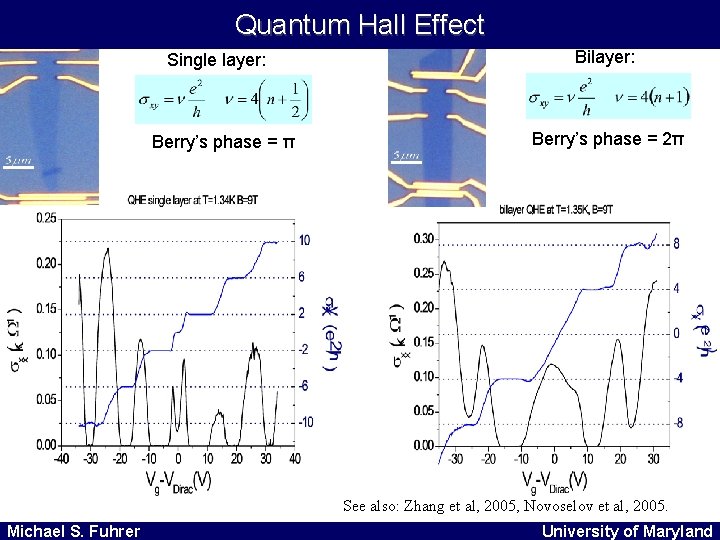
Quantum Hall. Quantum Effect: Single Layer vs. Bilayer Hall Effect Single layer: Berry’s phase = π Bilayer: Berry’s phase = 2π See also: Zhang et al, 2005, Novoselov et al, 2005. Michael S. Fuhrer University of Maryland