An Introduction to Computer Graphics Introduction Graphics Users

An Introduction to Computer Graphics

Introduction Graphics Users n n Group 1 - reasonable images produced quickly w flight simulation w games w Virtual Environments w CAD w data visualisation Group 2 - photorealistic images produced non-real time w advertising w Television w films

Graphics Process

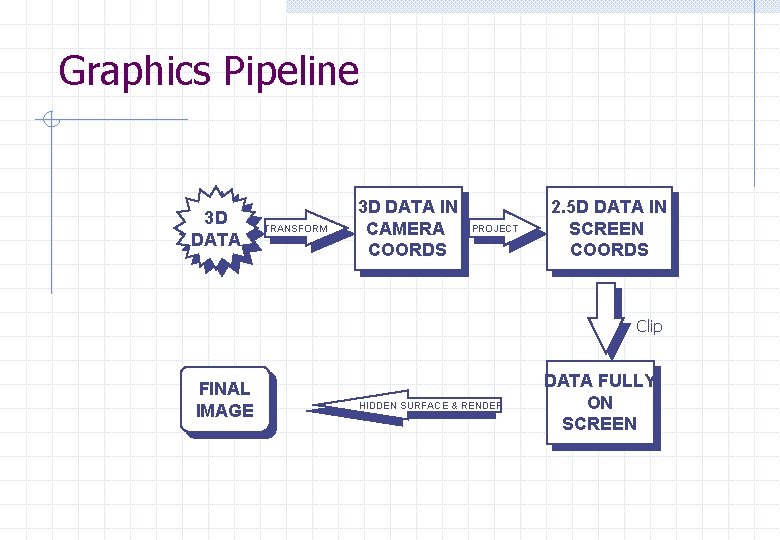
Graphics Pipeline 3 D DATA TRANSFORM 3 D DATA IN CAMERA COORDS PROJECT 2. 5 D DATA IN SCREEN COORDS Clip FINAL IMAGE HIDDEN SURFACE & RENDER DATA FULLY ON SCREEN

Scene Description WORLD n n n Objects Lights Camera OBJECTS n n n Shape Colour/Material Location

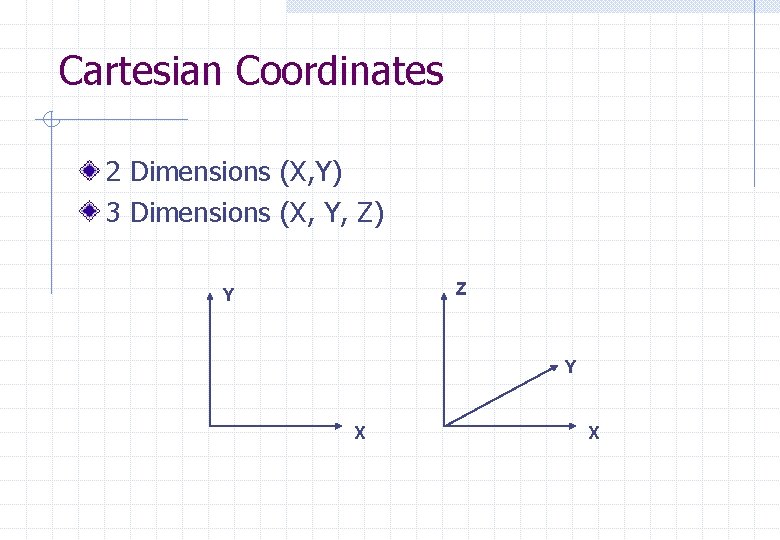
Cartesian Coordinates 2 Dimensions (X, Y) 3 Dimensions (X, Y, Z) Z Y Y X X

Object Representation POINTS (X, Y, Z) LINES (X 1, Y 1, Z 1), (X 2, Y 2, Z 2) POLYGONS (X 1, Y 1, Z 1). . . (Xn, Yn, Zn)

Object Representation MESHES n n n Set of Vertices V 1 = (X 1, Y 1, Z 1). . . Vn = (Xn, Yn, Zn) Set of Polygons P 1, P 2, . . . Pm Each polygon Pi is represented as a ordered list of vertices Vi 1, Vi 2, . . . Vir EXAMPLE

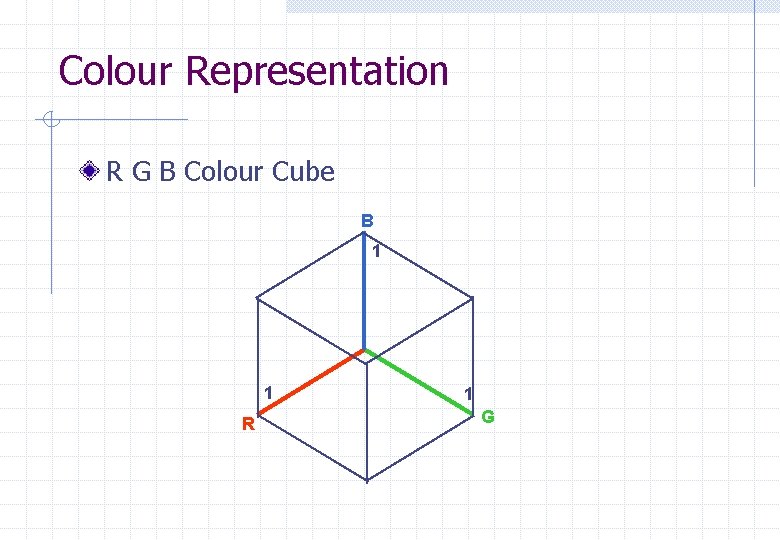
Object Colour RGB SYSTEM n n n RED - GREEN - BLUE ADDITIVE LIGHT SYSTEM COLOUR REPRESENTED AS (R, G, B) Each primary is between 0 and 1 EXAMPLES n n n (1, 1, 1) represents White (0, 0, 0) represents Black (1, 0, 0) represents all Red

Colour Representation R G B Colour Cube B 1 1 R 1 G

Building a World Built from a set of objects Objects translated into position Objects rotated as appropriate Objects scaled as appropriate Include light sources: n n n Ambient Non-directional Spotlight Include camera position and view direction

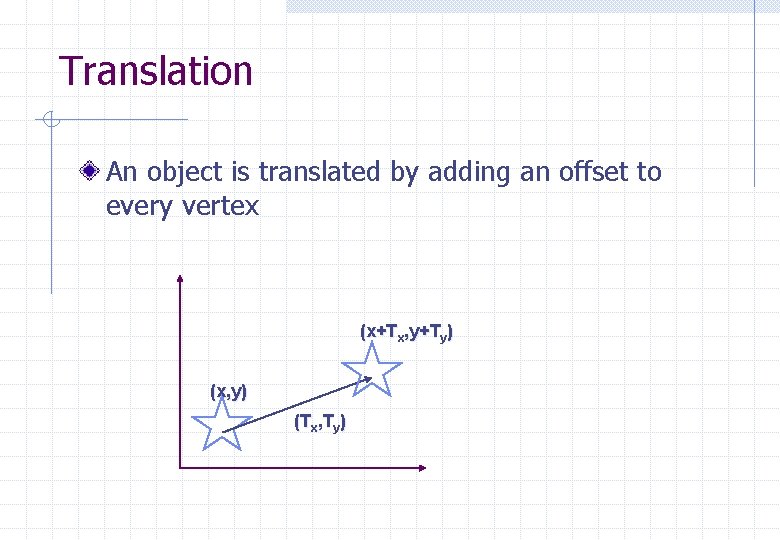
Transforming Objects TRANSLATION n ADD an offset to every vertex of an object ROTATION n n n Use trigonometry to calculate new position of each vertex Allow rotation around each Cartesian axis Rotation may be represented by matrices SCALE n n Multiply each vertex by a constant scale factor Always apply on an object BEFORE it is placed into the scene

Translation An object is translated by adding an offset to every vertex (x+Tx, y+Ty) (x, y) (Tx, Ty)

Matrix Rotation (2 Dimensions) (x 1, y 1) = cos(a) -sin(a) x sin(a) y cos(a) (x 1, y 1) a (x, y)

Matrix Rotation (3 Dimensions) Rotation about X by angle a Z (x 1, y 1, z 1) = 1 0 0 cos(a) -sin(a) cos(a) x y z a X Y

Matrix Rotation (3 Dimensions) Rotation about Y by angle a Z (x 1, y 1, z 1) = cos(a) 0 0 1 -sin(a) 0 cos(a) x y z a X Y

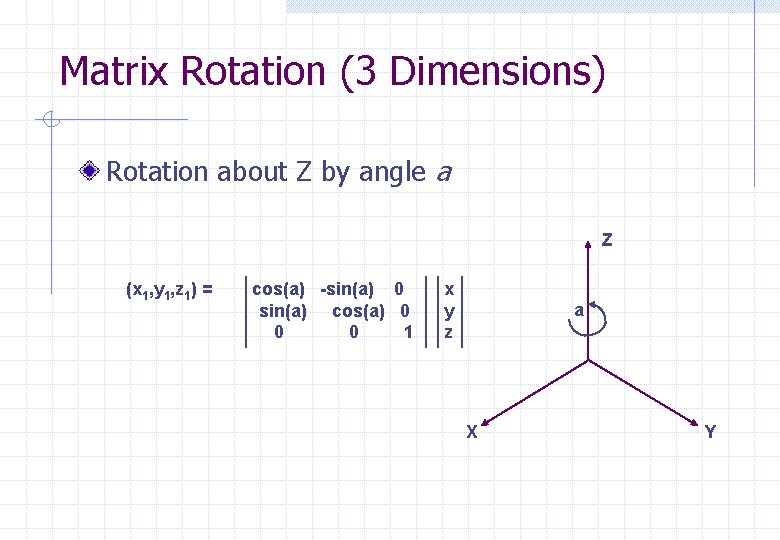
Matrix Rotation (3 Dimensions) Rotation about Z by angle a Z (x 1, y 1, z 1) = cos(a) -sin(a) 0 sin(a) cos(a) 0 0 0 1 x y z a X Y

Projection Objects exist in 3 dimensions, final image is in 2 dimensions Projection reduces the dimension by one Two common types: n n PERSPECTIVE w Mimics scaling of distance Orthographic w Objects not scaled with distance

Orthographic Objects projected with parallel lines

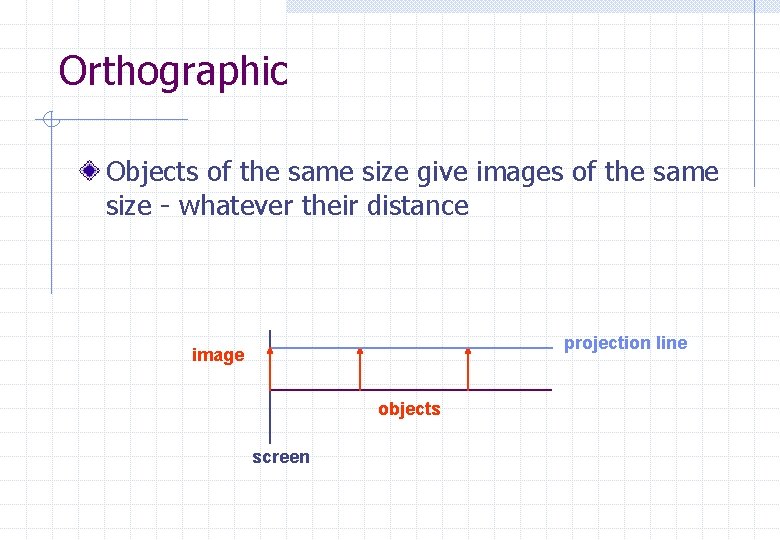
Orthographic Objects of the same size give images of the same size - whatever their distance projection line image objects screen

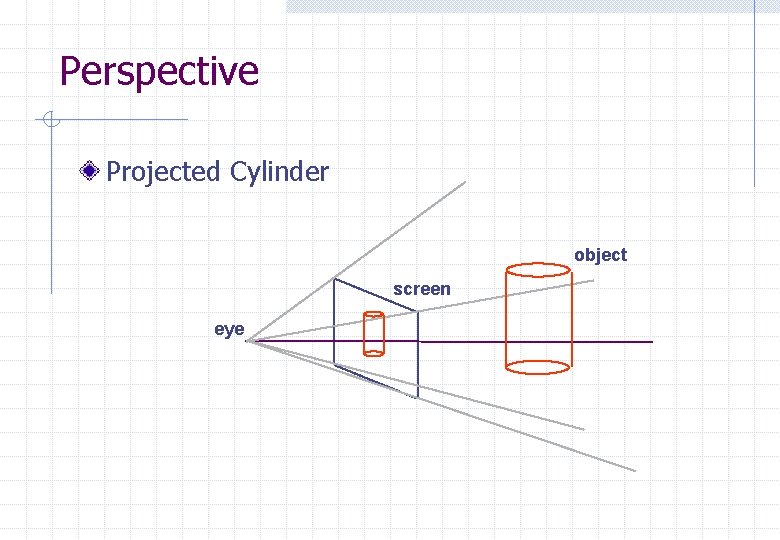
Perspective Projected Cylinder object screen eye

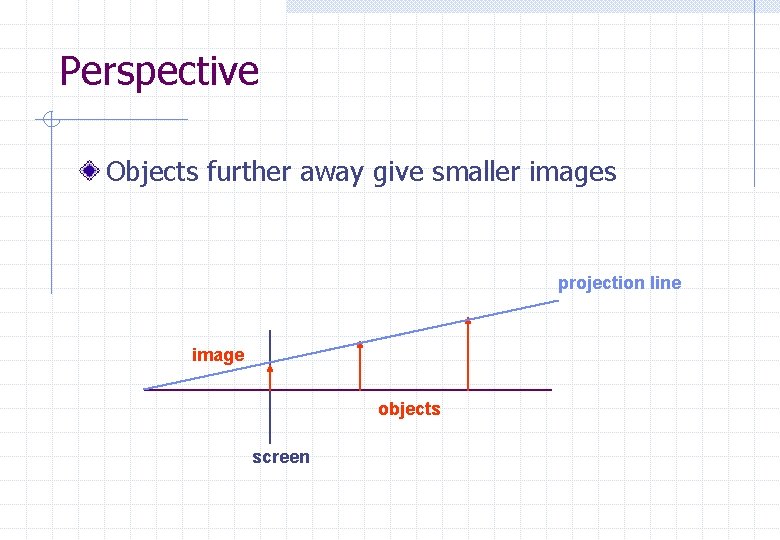
Perspective Objects further away give smaller images projection line image objects screen

Clipping Projected objects may lie: n n n Totally on the screen Partially on the screen Completely off the screen Polygons need to be clipped to the sides of the screen n n Care must be taken to ensure that the new polygon is complete Remaining polygons may obscure each other

Hidden Surface Removal Aim to identify which parts of a polygon are visible Many solutions developed for special cases Consider two examples: n n PAINTERS ALGORITHM Z-BUFFER

Screen Picture is drawn in a frame-buffer Frame-buffer is an area of memory Think of the screen as a grid of squares n n n Each square represents a pixel Every pixel can hold a colour (R, G, B) value Drawing a picture is just colouring the squares

Drawing Example Partially Drawn Polygon

Painters Algorithm Method n n Generate all the polygons Order them with respect to their distance from the camera Draw the polygons furthest away first, move towards the viewer Visible polygons drawn over distant polygons Designed for the case when polygons are well- ordered

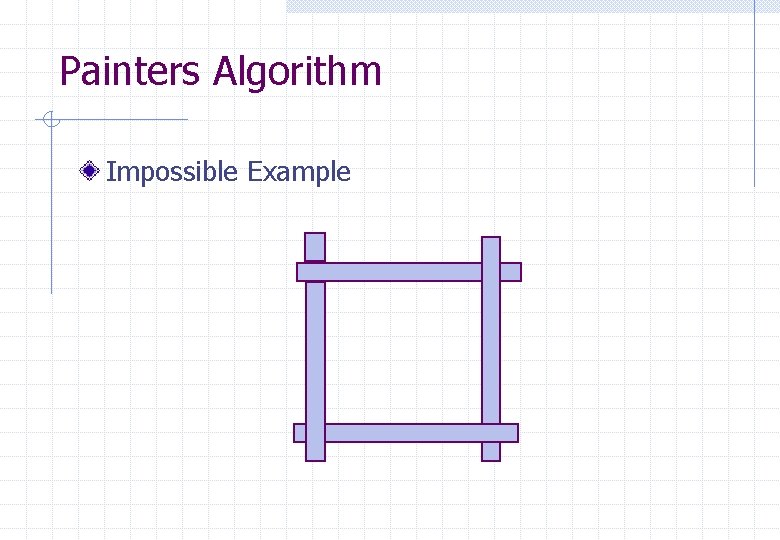
Painters Algorithm Impossible Example

Z-Buffer Algorithm Method n n n Retain distance information for each vertex Frame-buffer extended to have a depth-buffer Whilst drawing the polygon, calculate the pixel depth for each pixel FOR each pixel in polygon CALCULATE depth of pixel in polygon COMPARE depth with current frame-buffer depth IF polygon pixel CLOSER than frame-buffer depth THEN save polygon colour AND depth in frame-buffer w NEXT pixel w w

Illumination Model The illumination model allows the colour to be calculated at a surface Approximates the behavior of light within a scene Typical example is called the ‘Phong’ Model

Phong Illumination Model Considers three types of illumination n Ambient n Diffuse n Specular Provides the highlight on objects Constant background illumination w same for all objects in a scene w gives constant shading Light widely scattered by a surface w depends only upon the position of the light relative to the surface w depends on both the light position and the eye position

Ambient Example

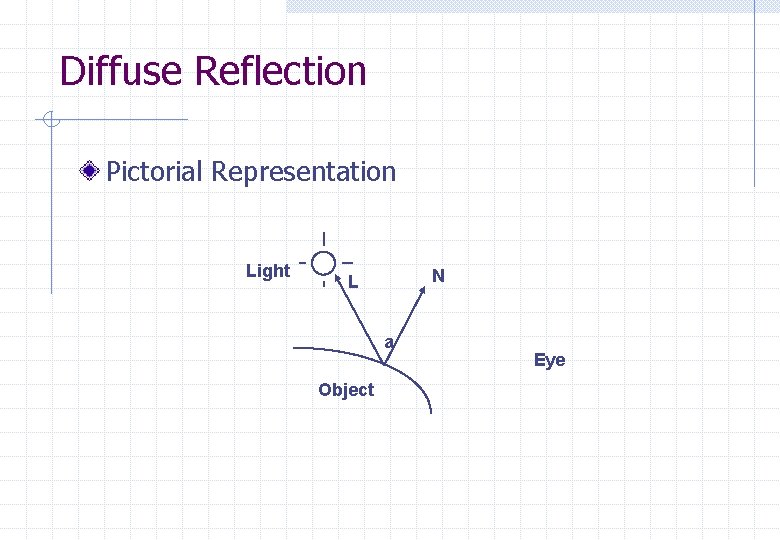
Diffuse Reflection Pictorial Representation Light N L a Object Eye

Diffuse Reflection Mathematical Description n N Li Ii kd ai n Component is given by: n n normal to object at intersection vector from intersection to light i intensity of light from light i coefficient of diffuse reflection angle between Li and N w kd(I 1(cos (a 1)) + l 2(cos(a 2)) + l 3(cos(a 3)) +. . . )

Diffuse Example

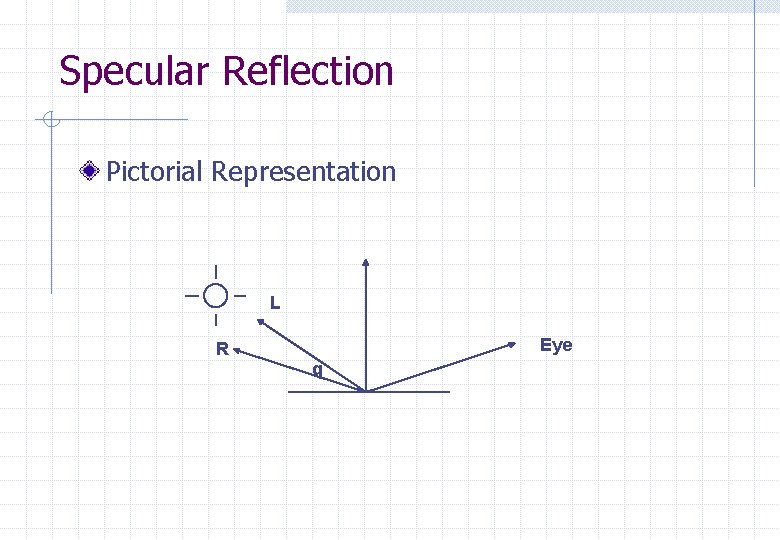
Specular Reflection Pictorial Representation L R Eye q

Specular Reflection Mathematical Description n n n ks Ii Li R n coefficient of specular reflection intensity of light from light i vector from intersection to light i direction of reflection of incident ray level of specularity Specular component given by w ks(I 1(L 1. R)n + I 2(L 2. R)n +. . . ) with L. R being the cosine of the angle between vectors L and R

Specular Example - 1

Specular Example - 2

Specular Example - 3

Full Shading Model The colour shading model is: n Ir = Iakar + Ii(kdr(Li. N) + ks(Li. R)n) n Ig = Ia. Kag + Ii(kdg(Li. N) + ks(Li. R)n) n Ib = Iakab + Ii(kdb(Li. N) + ks(Li. R)n) n The colour is expressed in terms of (Ir, Ig, Ib)

Object Shading Flat shading Gouraud shading Phong shading Texturing

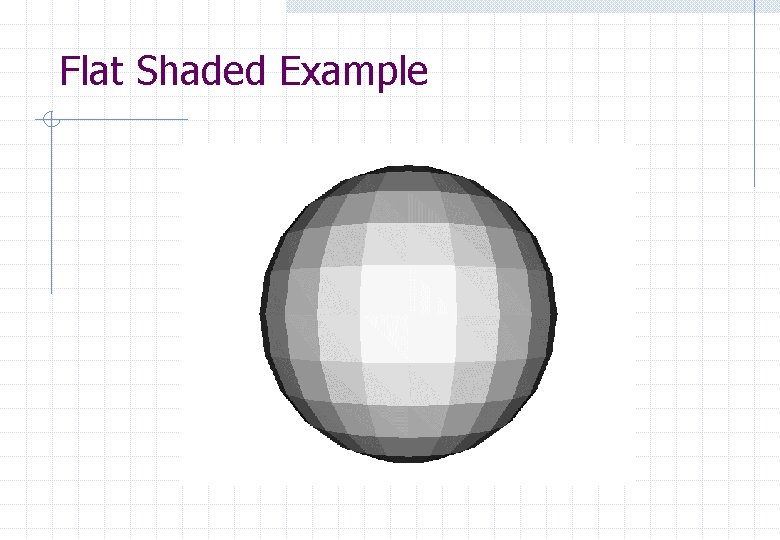
Flat Shaded Simplest way to shade a polygon Apply the Phong illumination model once All pixels in the polygon are shaded the same Quick, but limited realism for meshes

Flat Shaded Example

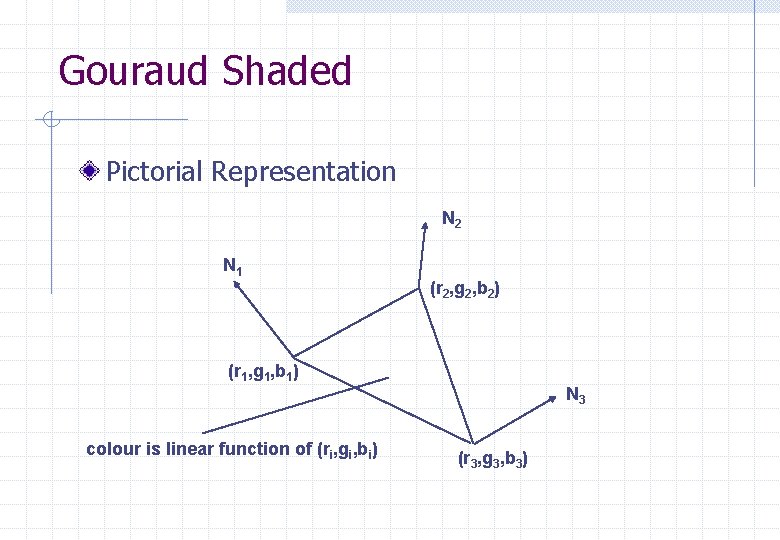
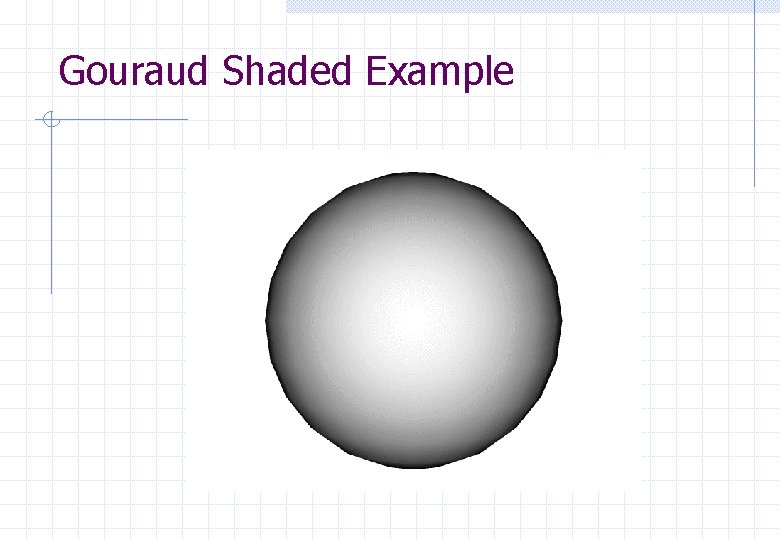
Gouraud Shaded Normal at each vertex of a polygon (r, g, b) colour computed for each vertex colour for pixels within the polygon are calculated by linear interpolation from the vertices Slower, smooth appearance across polygon

Gouraud Shaded Pictorial Representation N 2 N 1 (r 2, g 2, b 2) (r 1, g 1, b 1) colour is linear function of (ri, gi, bi) N 3 (r 3, g 3, b 3)

Gouraud Shaded Example

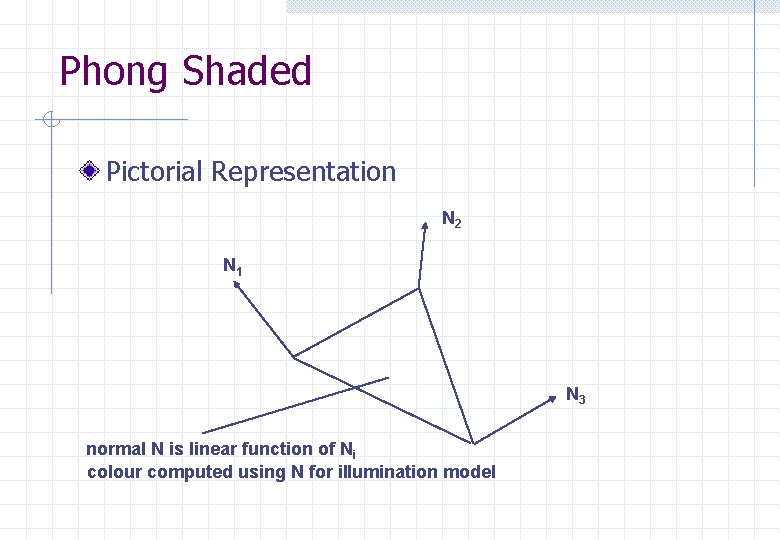
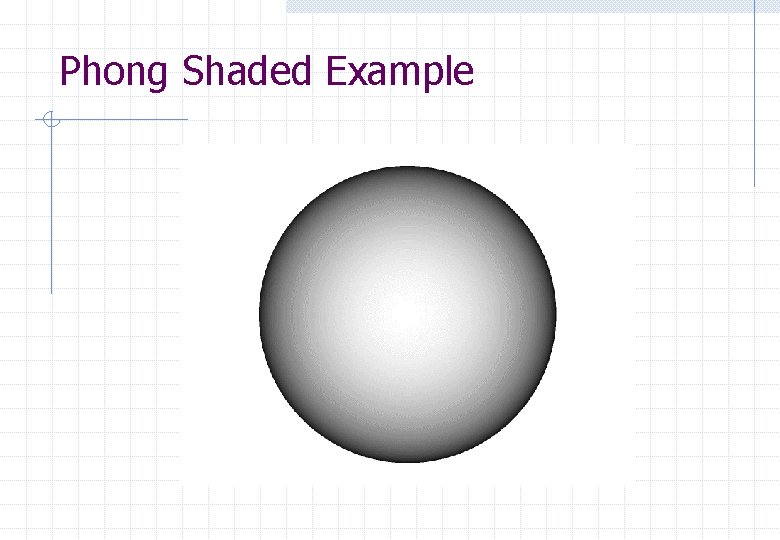
Phong Shaded Normal at each vertex of a polygon Normal for pixels within the polygon are calculated by linear interpolation from the vertices (r, g, b) colour calculated for each pixel Much slower, smooth appearance across polygon, removes some artifacts

Phong Shaded Pictorial Representation N 2 N 1 N 3 normal N is linear function of Ni colour computed using N for illumination model

Phong Shaded Example

Texturing 2 Dimensional Textures n n n Use an image mapped onto an object Either scale the image to fit once on the object or tile the object with a number of copies of the image Typically use: w plane map w cylindrical map w spherical map

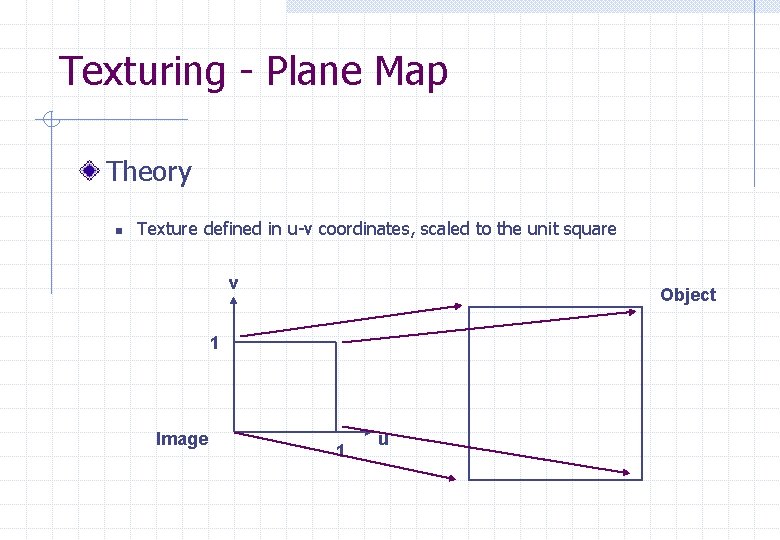
Texturing - Plane Map Theory n Texture defined in u-v coordinates, scaled to the unit square v Object 1 Image 1 u

Texturing - Plane Map

Texturing - Plane Map

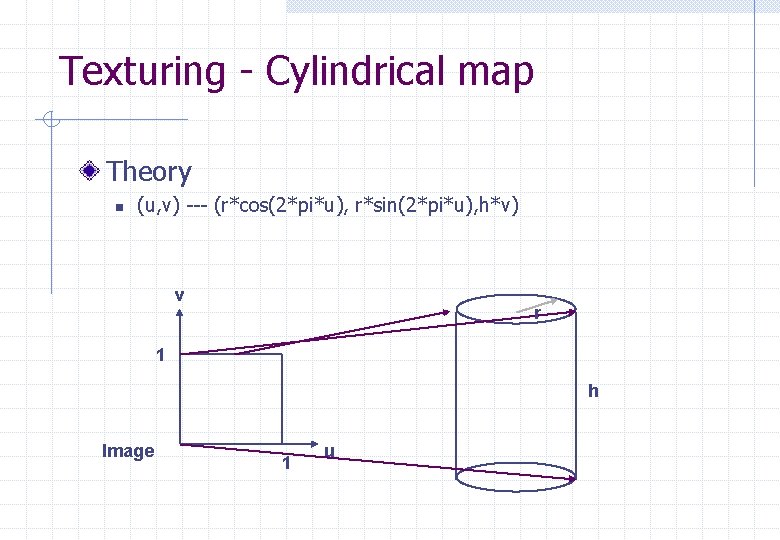
Texturing - Cylindrical map Theory n (u, v) --- (r*cos(2*pi*u), r*sin(2*pi*u), h*v) v r 1 h Image 1 u

Texturing - Cylindrical map Seam

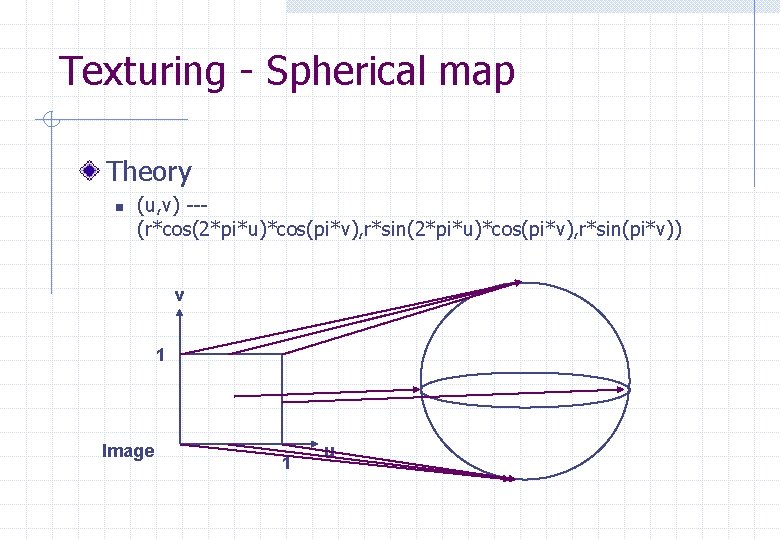
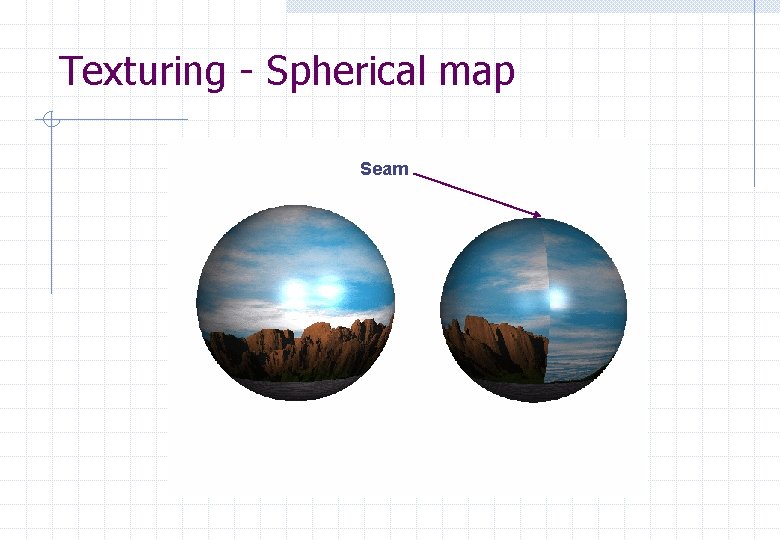
Texturing - Spherical map Theory n (u, v) --(r*cos(2*pi*u)*cos(pi*v), r*sin(pi*v)) v 1 Image 1 u

Texturing - Spherical map Seam

Texturing 3 Dimensional Textures n n 2 Dimensional textures only cover the surface of an object 3 Dimensional textures are defined for all points in space Objects are cut from the texture space - much like sculpting a statue from stone 3 Dimensional textures are often defined mathematically (r, g, b) = T(x, y, z) with T the texture function

Texturing Example

Texturing Example

Texturing Example

Texturing Example

Texturing Example

Texturing Example

Texturing Example

Alternative Rendering Techniques Ray tracing n n n Aims to improve realism of image Slower than polygon rendering Suitable for producing still images and animations Radiosity n n n Further improvement of the shading model Attempts to improve the treatment of ambient light Slow, but can be pre-computed and used with polygon rendering or ray tracing

Ray Tracing What’s wrong with the Graphics Pipeline n n n difficult to achieve realism reflections and transparency not accurate real shadows increase rendering time polygonal objects are not smooth ( Gouraud and Phong shading help ) difficult to render shapes defined mathematically the pipeline is not a natural approach

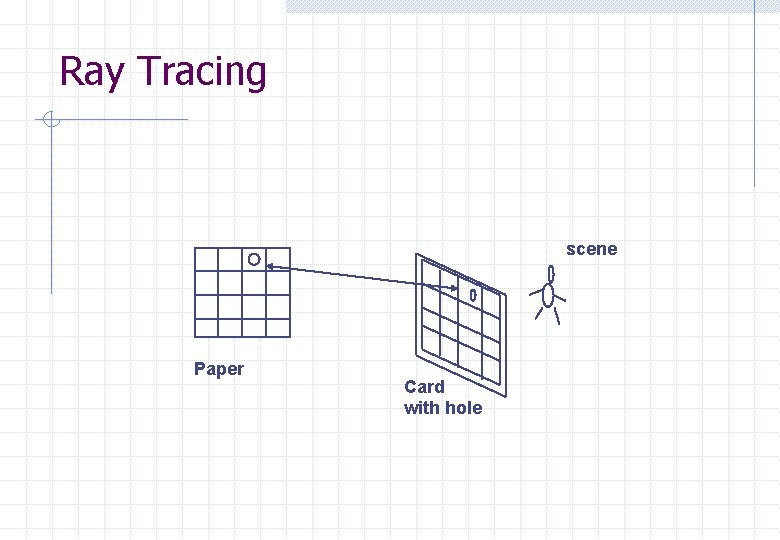
Ray Tracing Concept of Ray Tracing n n n draw a grid on some paper cut a square hole in a card and connect some wires across the hole, again forming a grid hold the card in front of the scene to be painted and draw the image seen through each grid square on the corresponding square on the paper if the image seen through a grid square is too complex, increase the number of squares on paper and card When the grid is suitably fine, just paint the average colour seen through a grid hole in the corresponding position on the paper

Ray Tracing scene Paper Card with hole

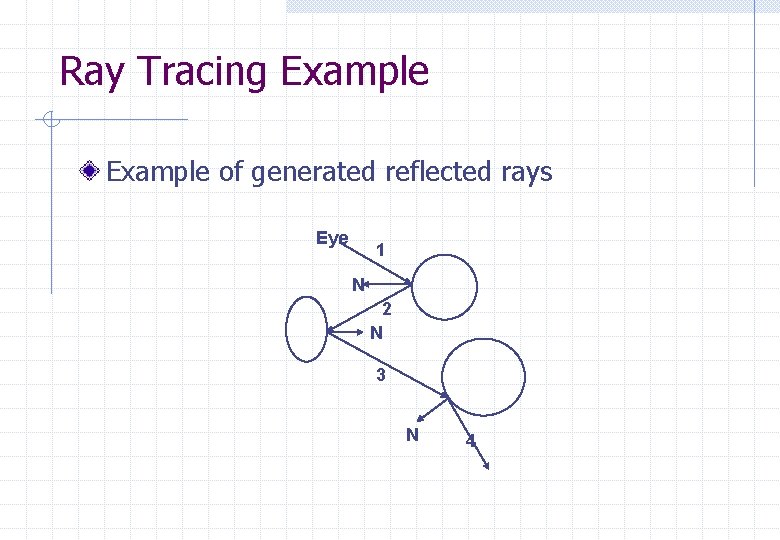
Ray Tracing Algorithm n n n Trace a ray from the eye through a pixel, into the scene Find the nearest object intersected by the ray cast a new reflected ray and refracted ray calculate light arriving from reflected, refracted rays and direct illumination from lights in the scene apply shading model to get the colour for the object at the intersection paint the pixel with the computed colour

Ray Tracing Example of generated reflected rays Eye 1 N 2 N 3 N 4

Ray Tracing Example

Ray Tracing Example

Radiosity is a physically based model of global diffuse illumination n n Developed at Cornell University in 1994 from radiative heat transfer Assumes all surfaces are ideal Lambertian (diffuse) - ray tracing assumes ideal specular Radiosity discretises the scenes and produces data independent of the viewer In general, Radiosity takes longer than ray tracing

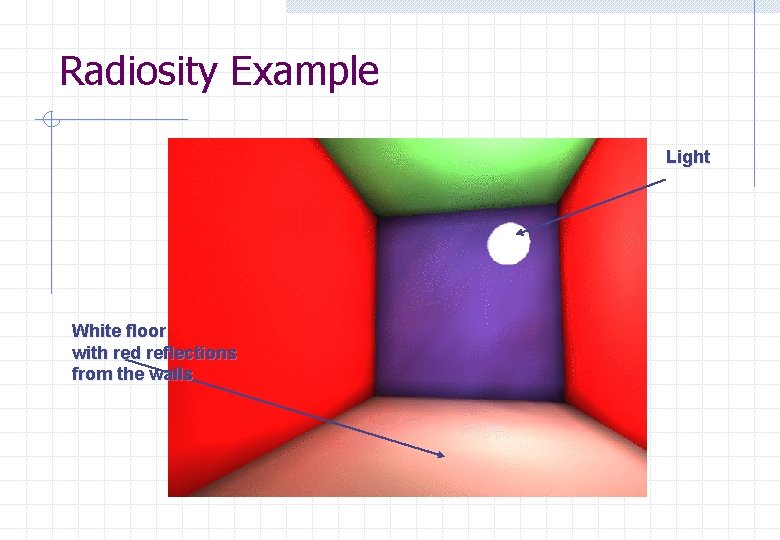
Radiosity is not a rendering technique n n n does not take into account the viewer position produces data to be rendered later needs rendering process to actually produce an image rendering can be done using a graphics pipeline or using ray tracing methods best results occur when radiosity and ray tracing are used an example of a benefit of radiosity is colour bleeding

Radiosity Example Light White floor with red reflections from the walls

Software Rendering Packages n n n POVRay Imagine Truespace 2 Animation Master 3 D Studio Max free from www. povray. org Impulse Caligari, www. caligari. com Martin Hash, www. hash. com Kinetix, www. ktx. com Libraries n n Open. GL VRML 2 Silicon Graphics, www. sgi. com Silicon Graphics, vrml. sgi. com