An Introduction to Computer Experiments and their Design

An Introduction to Computer Experiments and their Design Problems Tony O’Hagan University of Sheffield 8 Sept 2006, DEMA 2006 Slide 1

Outline 1. Computer codes and their problems 2. Gaussian process representation 3. Design 4. Conclusions www. mucm. group. shef. ac. uk 2

Models and uncertainty n In almost all fields of science, technology, industry and policy making, people use mechanistic models to describe complex realworld processes n For understanding, prediction, control n Growing realisation of importance of uncertainty in model predictions Can we trust them? n Without any quantification of output uncertainty, it’s easy to dismiss them n www. mucm. group. shef. ac. uk 3

Computer codes n A computer code is a software implementation of a mathematical model for some real process n Given suitable inputs x that define a particular instance, the code output y = f(x) predicts the true value of that real process n A single run of the model can take an appreciable amount of time In some cases, months! n Even a few seconds can be too long for tasks that require many thousands of runs n www. mucm. group. shef. ac. uk 4

What are models for? n Prediction and optimisation n What will the model output be for these inputs? n What inputs will optimise the output? n Uncertainty analysis n Given uncertainty in model inputs, how uncertain are outputs? n Which input uncertainties are most influential? n Calibration and data assimilation n How can we use data to improve the model? n Many of these tasks implicitly require many model runs www. mucm. group. shef. ac. uk 5

Computation n Consider uncertainty analysis n Given uncertain input X, what can we say about the distribution of output Y = f(X)? n Monte Carlo is the simplest method n Sample x 1, x 2, …, x. N from distribution of X n Run model to get outputs y 1, y 2, …, y. N n Use this as a sample of the output distribution n Easy to implement but impractical if model takes more than a few seconds to run n 10, 000 minutes is a week www. mucm. group. shef. ac. uk 6

Gaussian process representation n More efficient approach n First work in early 1980 s – DACE n Represent the code as an unknown function n f(. ) becomes a random process n We represent it as a Gaussian process n Training runs n Run model for sample of x values n Condition GP on observed data n Typically requires many fewer runs than MC n And x values don’t need to be chosen randomly www. mucm. group. shef. ac. uk 7

Bayesian formulation n Prior beliefs about function n conditional on hyperparameters n Data n Posterior beliefs about function n conditional on hyperparameters www. mucm. group. shef. ac. uk 8

Emulation n Analysis is completed by prior distributions for, and posterior estimation of, hyperparameters n Roughness parameters in B crucial n The posterior distribution is known as an emulator of the computer code Posterior mean estimates what the code would produce for any untried x (prediction) n With uncertainty about that prediction given by posterior variance n Correctly reproduces training data n www. mucm. group. shef. ac. uk 9

2 code runs n Consider one input and one output n Emulator estimate interpolates data n Emulator uncertainty grows between data points www. mucm. group. shef. ac. uk 10

3 code runs n Adding another point changes estimate and reduces uncertainty www. mucm. group. shef. ac. uk 11

5 code runs n And so on www. mucm. group. shef. ac. uk 12

Frequentist formulation n Pretend the function is actually sampled from a Gaussian process population of functions Absurd, really! n But properties of inferences depend on it n n Best linear unbiased predictor is the same as Bayesian posterior mean With weak prior distributions n Similarly for variances n www. mucm. group. shef. ac. uk 13

Then what? n Use the emulator to make inference about other things of interest n E. g. uncertainty analysis, calibration n Conceptually very straightforward in the Bayesian framework But of course can be computationally hard n Frequentist approach has not generally been extended to some of the more complex analyses n www. mucm. group. shef. ac. uk 14

Design n The design problem is to choose x 1, x 2, …, x. N n Design space is usually rectangular n Often rather arbitrary n May be high dimensional n Objective is to build an accurate emulator across n Formally optimising for some specific analysis is generally inappropriate (and too hard) n Usual approach is to aim for a design that fills uniformly n Minimises uncertainty between design points www. mucm. group. shef. ac. uk 15

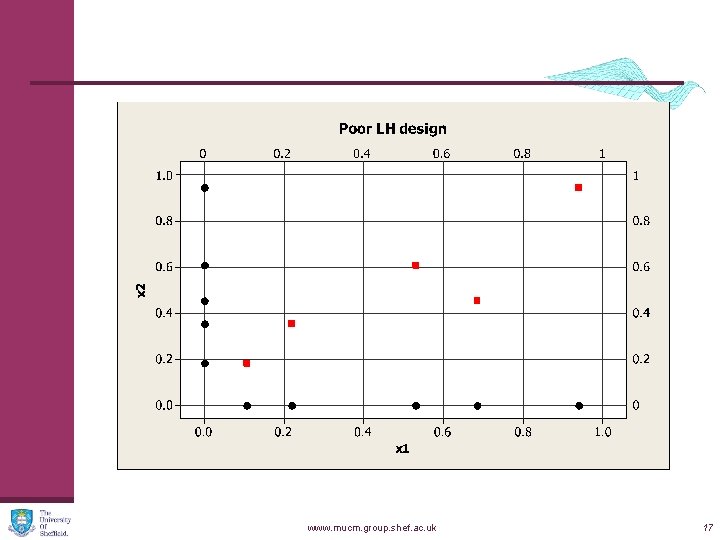
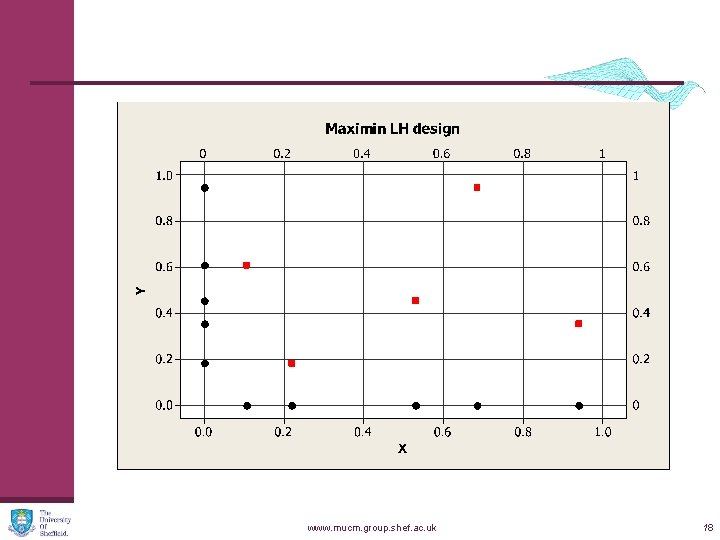
Latin hypercubes n LH designs n Divide the range of each variable into N equal segments n Choose a value in each segment (uniformly) n Permute each coordinate randomly n Covers each coordinate evenly n Maximin LH n Generate many LH designs n Choose one for which minimum distance between points is greatest www. mucm. group. shef. ac. uk 16

www. mucm. group. shef. ac. uk 17

www. mucm. group. shef. ac. uk 18

Projection n Projections of LH designs onto lower dimensional spaces are also LH designs Not necessarily maximin, but usually quite even n Important because typically only a few inputs are influential n n There are other ways of generating space- filling designs Low discrepancy sequences n Don’t necessarily have good projections n www. mucm. group. shef. ac. uk 19

Other considerations n Maximin LH designs don’t have points close together By definition! n But such pairs help to identify hyperparameters n n n Particularly roughness parameters Maybe add extra points differing from existing ones only by a small amount in one dimension n Sequential designs would be very helpful n Low discrepancy sequences n Adaptive designs for partitioned emulators www. mucm. group. shef. ac. uk 20

Some design challenges n Space filling designs that are good in all projections n Understanding the value of low-distance pairs n Designs for non-rectangular or unbounded n Sequential/adaptive design E. g. a good 150 -point design with a good 100 point subset n Adaptation to roughnesses and heterogeneity n n Design of real-world experiments for calibration www. mucm. group. shef. ac. uk 21

MUCM n This is a substantial and topical research area n MUCM (Managing Uncertainty in Complex Models) is a new £ 2 M research project Funded by RCUK Basic Technology scheme n 4 year grant, 7 RAs + 4 Ph. Ds in 5 centres n Henry Wynn (LSE) leading design work n n n But enough problems for lots of people to work on! mucm. group. shef. ac. uk n Year-long programme at SAMSI (USA) www. mucm. group. shef. ac. uk 22