An Introduction to Bioinformatics Algorithms www bioalgorithms info

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Finding Regulatory Motifs in DNA Sequences

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Outline • • • Implanting Patterns in Random Text Gene Regulation Regulatory Motifs The Motif Finding Problem Brute Force Motif Finding The Median String Problem Search Trees Branch-and-Bound Motif Search Branch-and-Bound Median String Search Consensus and Pattern Branching: Greedy Heuristics PMS: Exhaustive Motif Search

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Random Sample atgaccgggatactgataccgtatttggcctaggcgtacacattagataaacgtatgaagtacgttagactcggcgccgccg acccctattttttgagcagatttagtgacctggaaaatttgagtacaaaacttttccgaatactgggcataaggtaca tgagtatccctgggatgacttttgggaacactatagtgctctcccgatttttgaatatgtaggatcattcgccagggtccga gctgagaattggatgaccttgtaagtgttttccacgcaatcgcgaaccaacgcggacccaaaggcaagaccgataaaggaga tcccttttgcggtaatgtgccgggaggctggttacgtagggaagccctaacggacttaatggcccacttagtccacttatag gtcaatcatgttcttgtgaatggatttttaactgagggcatagaccgcttggcgcacccaaattcagtgtgggcgagcgcaa cggttttggcccttgttagaggcccccgtactgatggaaactttcaattatgagagagctaatctatcgcgtgttcat aacttgagttggtttcgaaaatgctctggggcacatacaagaggagtcttccttatcagttaatgctgtatgacactatgta ttggcccattggctaaaagcccaacttgacaaatggaagatagaatccttgcatttcaacgtatgccgaaagggaag ctggtgagcaacgacagattcttacgtgcattagctcgcttccggggatctaatagcacgaagcttctgggtactgatagca

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Implanting Motif AAAAAAAGGGGGGG atgaccgggatactgat. AAAAGGGGGGGggcgtacacattagataaacgtatgaagtacgttagactcggcgccgccg acccctattttttgagcagatttagtgacctggaaaatttgagtacaaaacttttccgaata AAAAGGGGGGGa tgagtatccctgggatgactt. AAAAGGGGGGGtgctctcccgatttttgaatatgtaggatcattcgccagggtccga gctgagaattggatg. AAAAGGGGGGGtccacgcaatcgcgaaccaacgcggacccaaaggcaagaccgataaaggaga tcccttttgcggtaatgtgccgggaggctggttacgtagggaagccctaacggacttaat AAAAGGGGGGGcttatag gtcaatcatgttcttgtgaatggattt. AAAAGGGGGGGgaccgcttggcgcacccaaattcagtgtgggcgagcgcaa cggttttggcccttgttagaggcccccgt. AAAAGGGGGGGcaattatgagagagctaatctatcgcgtgttcat aacttgagtt. AAAAGGGGGGGctggggcacatacaagaggagtcttccttatcagttaatgctgtatgacactatgta ttggcccattggctaaaagcccaacttgacaaatggaagatagaatccttgcat AAAAGGGGGGGaccgaaagggaag ctggtgagcaacgacagattcttacgtgcattagctcgcttccggggatctaatagcacgaagctt AAAAGGGGGGGa

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Where is the Implanted Motif? atgaccgggatactgataaaagggggcgtacacattagataaacgtatgaagtacgttagactcggcgccgccg acccctattttttgagcagatttagtgacctggaaaatttgagtacaaaacttttccgaataaaaaggggggga tgagtatccctgggatgacttaaaagggggggtgctctcccgatttttgaatatgtaggatcattcgccagggtccga gctgagaattggatgaaaagggggggtccacgcaatcgcgaaccaacgcggacccaaaggcaagaccgataaaggaga tcccttttgcggtaatgtgccgggaggctggttacgtagggaagccctaacggacttaataaaagggggggcttatag gtcaatcatgttcttgtgaatggatttaaaaggggaccgcttggcgcacccaaattcagtgtgggcgagcgcaa cggttttggcccttgttagaggcccccgtaaaagggggggcaattatgagagagctaatctatcgcgtgttcat aacttgagttaaaagggggggctggggcacatacaagaggagtcttccttatcagttaatgctgtatgacactatgta ttggcccattggctaaaagcccaacttgacaaatggaagatagaatccttgcataaaagggggggaccgaaagggaag ctggtgagcaacgacagattcttacgtgcattagctcgcttccggggatctaatagcacgaagcttaaaaggggggga

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Implanting Motif AAAAAAGGGGGGG with Four Mutations atgaccgggatactgat. Ag. AAAGGtt. GGGggcgtacacattagataaacgtatgaagtacgttagactcggcgccgccg acccctattttttgagcagatttagtgacctggaaaatttgagtacaaaacttttccgaata c. AAt. AAAAc. GGGa tgagtatccctgggatgactt. AAAAt. GGa. Gt. GGtgctctcccgatttttgaatatgtaggatcattcgccagggtccga gctgagaattggatgc. AAAAAAAGGGatt. Gtccacgcaatcgcgaaccaacgcggacccaaaggcaagaccgataaaggaga tcccttttgcggtaatgtgccgggaggctggttacgtagggaagccctaacggacttaat At. AAAGGaa. GGGcttatag gtcaatcatgttcttgtgaatggattt. AAc. AAt. AAGGGct. GGgaccgcttggcgcacccaaattcagtgtgggcgagcgcaa cggttttggcccttgttagaggcccccgt. AAAc. AAGGa. GGGccaattatgagagagctaatctatcgcgtgttcat aacttgagtt. AAAAAAt. AGGGa. Gccctggggcacatacaagaggagtcttccttatcagttaatgctgtatgacactatgta ttggcccattggctaaaagcccaacttgacaaatggaagatagaatccttgcat Act. AAAAAGGa. Gc. GGaccgaaagggaag ctggtgagcaacgacagattcttacgtgcattagctcgcttccggggatctaatagcacgaagctt Act. AAAAAGGa. Gc. GGa

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Where is the Motif? ? ? atgaccgggatactgatagaagaaaggttgggggcgtacacattagataaacgtatgaagtacgttagactcggcgccgccg acccctattttttgagcagatttagtgacctggaaaatttgagtacaaaacttttccgaatacaataaaacggcggga tgagtatccctgggatgacttaaaataatggagtggtgctctcccgatttttgaatatgtaggatcattcgccagggtccga gctgagaattggatgcaaaaaaagggattgtccacgcaatcgcgaaccaacgcggacccaaaggcaagaccgataaaggaga tcccttttgcggtaatgtgccgggaggctggttacgtagggaagccctaacggacttaataaagggcttatag gtcaatcatgttcttgtgaatggatttaacaataagggctgggaccgcttggcgcacccaaattcagtgtgggcgagcgcaa cggttttggcccttgttagaggcccccgtataaacaaggagggccaattatgagagagctaatctatcgcgtgttcat aacttgagttaaaaaatagggagccctggggcacatacaagaggagtcttccttatcagttaatgctgtatgacactatgta ttggcccattggctaaaagcccaacttgacaaatggaagatagaatccttgcatactaaaaaggagcggaccgaaagggaag ctggtgagcaacgacagattcttacgtgcattagctcgcttccggggatctaatagcacgaagcttactaaaaaggagcgga

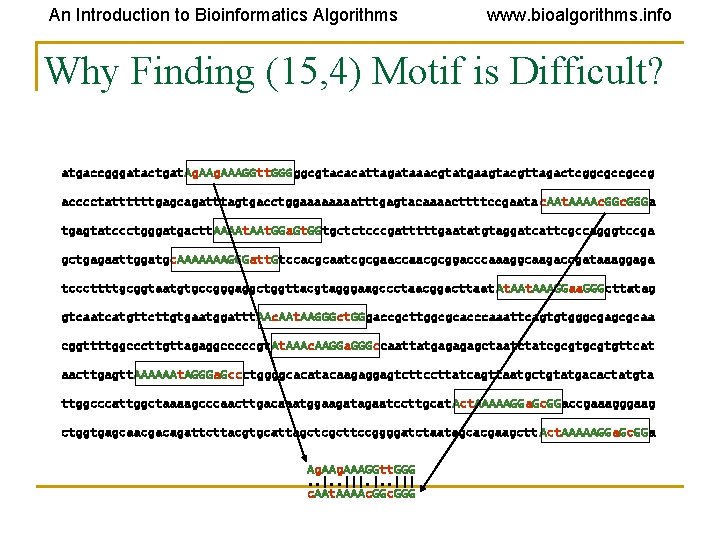
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Why Finding (15, 4) Motif is Difficult? atgaccgggatactgat. Ag. AAAGGtt. GGGggcgtacacattagataaacgtatgaagtacgttagactcggcgccgccg acccctattttttgagcagatttagtgacctggaaaatttgagtacaaaacttttccgaata c. AAt. AAAAc. GGGa tgagtatccctgggatgactt. AAAAt. GGa. Gt. GGtgctctcccgatttttgaatatgtaggatcattcgccagggtccga gctgagaattggatgc. AAAAAAAGGGatt. Gtccacgcaatcgcgaaccaacgcggacccaaaggcaagaccgataaaggaga tcccttttgcggtaatgtgccgggaggctggttacgtagggaagccctaacggacttaat At. AAAGGaa. GGGcttatag gtcaatcatgttcttgtgaatggattt. AAc. AAt. AAGGGct. GGgaccgcttggcgcacccaaattcagtgtgggcgagcgcaa cggttttggcccttgttagaggcccccgt. AAAc. AAGGa. GGGccaattatgagagagctaatctatcgcgtgttcat aacttgagtt. AAAAAAt. AGGGa. Gccctggggcacatacaagaggagtcttccttatcagttaatgctgtatgacactatgta ttggcccattggctaaaagcccaacttgacaaatggaagatagaatccttgcat Act. AAAAAGGa. Gc. GGaccgaaagggaag ctggtgagcaacgacagattcttacgtgcattagctcgcttccggggatctaatagcacgaagctt Act. AAAAAGGa. Gc. GGa Ag. AAAGGtt. GGG. . |||. |. . ||| c. AAt. AAAAc. GGG

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info (Old) Challenging Problem • Find a motif in a sample of - 20 “random” sequences (e. g. 600 nt long) - each sequence containing an implanted pattern of length 15 (called motif instance) - each pattern appearing with 4 mismatches as a (15, 4)-motif instance

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Combinatorial Gene Regulation • A DNA microarray experiment showed that when gene X is knocked out, 20 other genes are not expressed (or transcribed) • How can one gene have such drastic effects?

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Regulatory Proteins • Gene X encodes a regulatory protein, a. k. a. a transcription factor (TF) • The 20 unexpressed genes rely on gene X’s TF simply TF X) to induce transcription • A single TF may regulate multiple genes (or

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Regulatory (or Control) Regions • Every gene contains a regulatory region (RR) typically stretching 100 -1000 bps upstream of the transcriptional start site (TSS), also called the promoter that helps to initiate the transcription of the gene • Another kind of RRs are enhancers, which could stretch over 50 kbps and help activate or inhibit the transcription of genes • Located within the RRs are the Transcription Factor Binding Sites (TFBS’s), which are short string patterns, also known as motifs, specific to each transcription factor (TF) • Each TF influences gene expression by binding to its specific sites in the target genes’ RRs

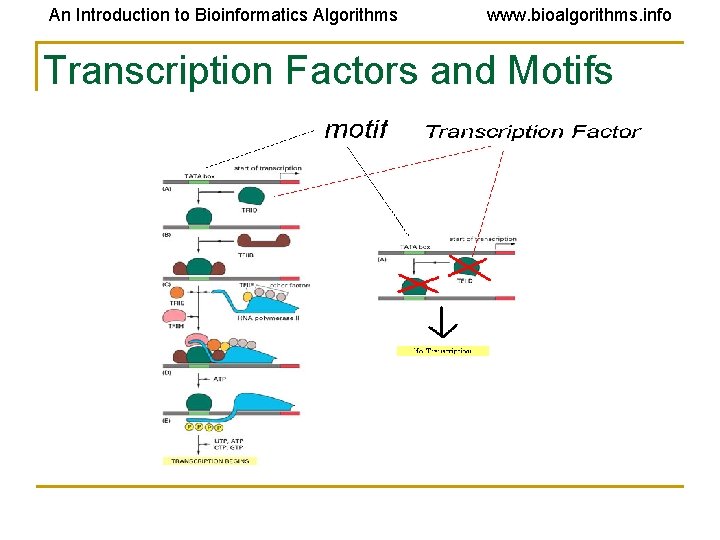
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Transcription Factors and Motifs

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Transcription Factor Binding Sites • A TFBS can be located anywhere within a regulatory region • A TFBS may vary slightly across different regulatory regions (or even within the same promoter or enhancer) since non-essential bases could mutate

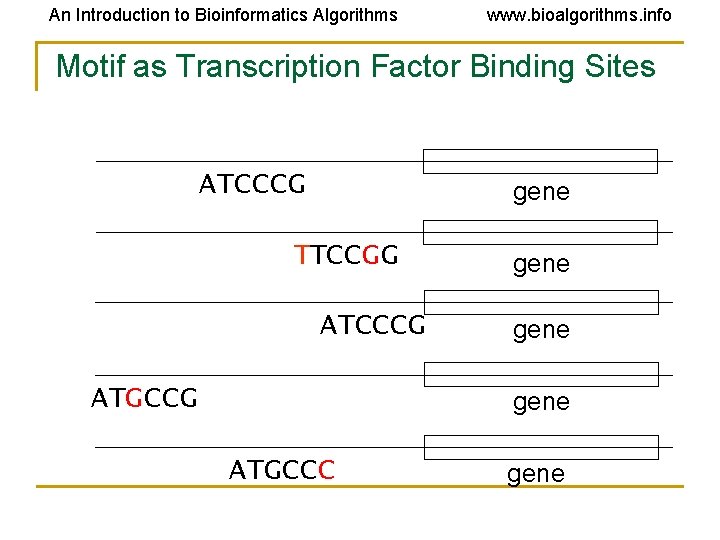
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Motif as Transcription Factor Binding Sites ATCCCG gene TTCCGG ATCCCG ATGCCG gene ATGCCC gene

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Motif Logos • Motifs can mutate on nonimportant bases • The five motif instances in five different (co-regulated) genes have mutations at positions 3 and 5 • Representations called motif logos illustrate the conserved and variable regions of a motif TGGGGGA TGAGAGA TGAGGGA

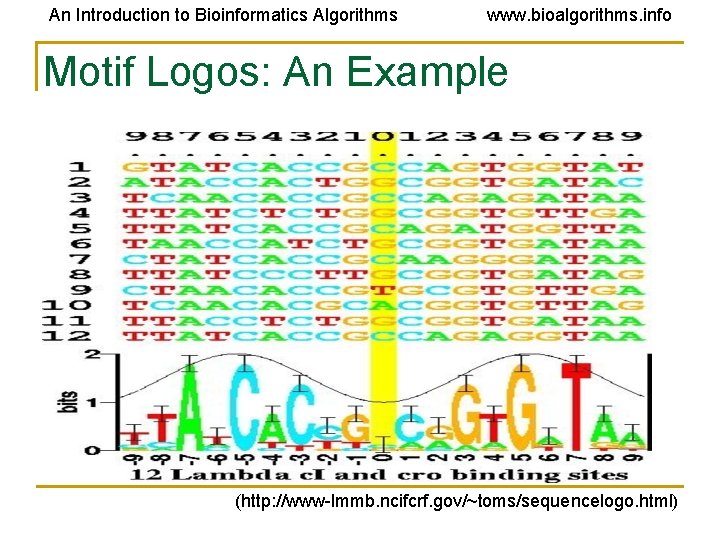
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Motif Logos: An Example (http: //www-lmmb. ncifcrf. gov/~toms/sequencelogo. html)

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Identifying Regulatory Motifs • Genes are turned on or off by regulatory proteins (TFs) • These proteins bind to upstream regulatory regions (RRs) of genes to either attract or block the RNA polymerase • Each TF binds to certain short DNA sequences (TFBS’s) that form a motif • Since co-regulated genes may share the same motif, their RR sequences are collected for the search of a motif

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Identifying Motifs: Complications • We do not know the motif sequence • We do not know where it is located relative to a gene’s transcription start site, if it occurs • A motif may appear slightly differently from one gene to the next • How to discern it from “random” motifs?

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info A Motif Finding Analogy • The Motif Finding Problem is similar to the problem posed by Edgar Allan Poe (1809 – 1849) in his Gold Bug story

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info The Motif Finding Problem • Given a random sample of DNA sequences (e. g. , RRs of co-regulated genes): cctgatagacgctatctggctatccacgtaggtcctctgtgcgaatctatgcgtttccaaccat agtactggtgtacatttgatacgtacaccggcaacctgaaacgctcagaaccagaagtgc aaacgtgcaccctcttcgtggctctggccaacgagggctgatgtataagacgaaaatttt agcctccgatgtaagtcatagctgtaactattacctgccacccctattacatcttacgtataca ctgttatacaacgcgtcatggcggggtatgcgttttggtcgtcgtacgctcgatcgttaacgtc • Find the pattern that is implanted in each of the individual sequences, namely, the motif

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info The Motif Finding Problem (cont’d) Additional information: • The hidden sequence is of length 8 • The pattern is not exactly the same in each sequence because random point mutations may occur in the sequences • The pattern appears once in each sequence

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info The Motif Finding Problem (cont’d) • Patterns revealed with no mutations: cctgatagacgctatctggctatccacgtaggtcctctgtgcgaatctatgcgtttccaaccat agtactggtgtacatttgatacgtacaccggcaacctgaaacgctcagaaccagaagtgc aaacgtgcaccctcttcgtggctctggccaacgagggctgatgtataagacgaaaatttt agcctccgatgtaagtcatagctgtaactattacctgccacccctattacatcttacgtataca ctgttatacaacgcgtcatggcggggtatgcgttttggtcgtcgtacgctcgatcgttaacgtc acgt consensus string

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info The Motif Finding Problem (cont’d) • Patterns with 2 point mutations: cctgatagacgctatctggctatcca. Ggtac. Ttaggtcctctgtgcgaatctatgcgtttccaaccat agtactggtgtacatttgat. Cc. Atacgtacaccggcaacctgaaacgctcagaaccagaagtgc aaacgt. TAgtgcaccctcttcgtggctctggccaacgagggctgatgtataagacgaaaatttt agcctccgatgtaagtcatagctgtaactattacctgccacccctattacatcttacgt. Cc. Atataca ctgttatacaacgcgtcatggcggggtatgcgttttggtcgtcgtacgctcgatcgtta. Ccgtacg. Gc

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info The Motif Finding Problem (cont’d) • Patterns with 2 point mutations: cctgatagacgctatctggctatcca. Ggtac. Ttaggtcctctgtgcgaatctatgcgtttccaaccat agtactggtgtacatttgat. Cc. Atacgtacaccggcaacctgaaacgctcagaaccagaagtgc aaacgt. TAgtgcaccctcttcgtggctctggccaacgagggctgatgtataagacgaaaatttt agcctccgatgtaagtcatagctgtaactattacctgccacccctattacatcttacgt. Cc. Atataca ctgttatacaacgcgtcatggcggggtatgcgttttggtcgtcgtacgctcgatcgtta. Ccgtacg. Gc Can we still find the motif, now that we have 2 mutations?

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Representing Motifs • We consider the location of each occurrence of the motif (called a motif instance) • The motif start positions in all sequences are represented as s = (s 1, s 2, …, st) • This is complete but not very intuitive

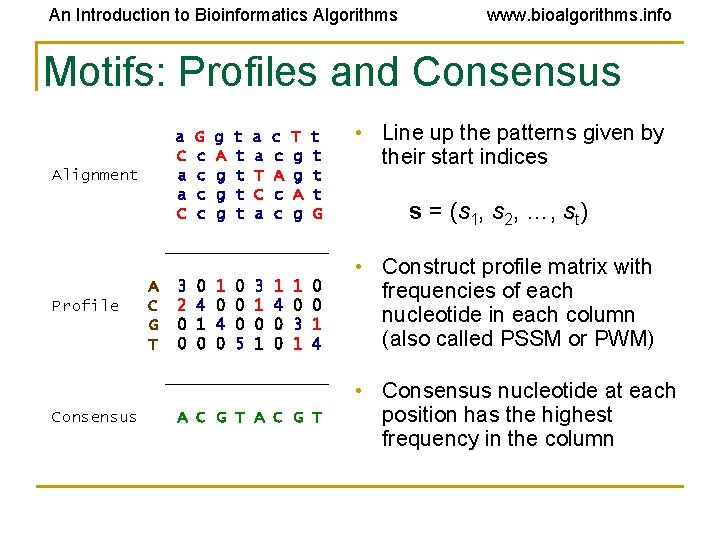
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Motifs: Profiles and Consensus a C a a C Alignment G c c g A g g g t t t a a T C a c c A c c T g g A g t t G _________ Profile A C G T 3 2 0 0 0 4 1 0 4 0 0 5 3 1 0 1 1 4 0 0 1 0 3 1 0 0 1 4 _________ Consensus A C G T • Line up the patterns given by their start indices s = (s 1, s 2, …, st) • Construct profile matrix with frequencies of each nucleotide in each column (also called PSSM or PWM) • Consensus nucleotide at each position has the highest frequency in the column

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Consensus • Think of consensus as an “ancestral” motif, from which mutated motifs emerged • The distance between a motif instance and the consensus sequence is generally less than that between two motif instances

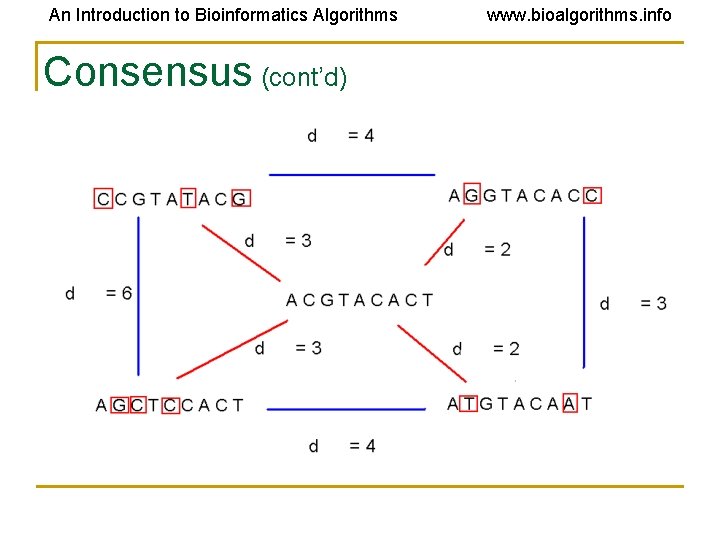
An Introduction to Bioinformatics Algorithms Consensus (cont’d) www. bioalgorithms. info

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Evaluating Motifs • We have a guess about the motif, but how “good” is this motif? • Need to introduce a scoring function to compare different guesses to allow us to choose the “best” one.

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Defining Some Terms • t - number of sample DNA sequences • n - length of each DNA sequence • DNA - sample of (co-regulated) DNA sequences (t x n array of nucleotides) • l - length of the motif (l-mer) • si - starting position of the motif in sequence i • s = (s 1, s 2, …, st) - vector of motif’s starting positions

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Parameters l=8 DNA cctgatagacgctatctggctatcca. Ggtac. Ttaggtcctctgtgcgaatctatgcgtttccaaccat agtactggtgtacatttgat. Cc. Atacgtacaccggcaacctgaaacgctcagaaccagaagtgc t=5 aaacgt. TAgtgcaccctcttcgtggctctggccaacgagggctgatgtataagacgaaaatttt agcctccgatgtaagtcatagctgtaactattacctgccacccctattacatcttacgt. Cc. Atataca ctgttatacaacgcgtcatggcggggtatgcgttttggtcgtcgtacgctcgatcgtta. Ccgtacg. Gc n = 69 s s 1 = 26 s 2 = 21 s 3= 3 s 4 = 56 s 5 = 60

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Scoring Motifs l • Given s = (s 1, …, st) and DNA: a G g t a c T t C c A t a c g t T A g t a c g t C c A t C c g t a c g G _________ Score(s, DNA) = A C G T Consensus Score t 3 0 1 0 3 1 1 0 2 4 0 0 1 4 0 0 0 3 1 0 0 0 5 1 0 1 4 _________ a c g t 3+4+4+5+3+4=30

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info The Motif Finding Problem • If starting positions s=(s 1, s 2, … st) are given, finding consensus is easy even with mutations in the sequences because we can simply construct the profile matrix and find the resultant consensus • But… the starting positions s are usually not given. How can we find the “best” profile matrix or consensus?

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info The Motif Finding Problem: Formulation • Goal: Given a set of DNA sequences, find a set of l -mers, one from each sequence, that maximizes the consensus score • Input: A t x n matrix of DNA and l, the length of the pattern to find • Output: A vector of t starting positions s = (s 1, s 2, …, st) maximizing Score(s, DNA)

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info The Motif Finding Problem: Brute Force Solution • Compute the scores for each possible combination of starting positions s • The best score will determine the best motif (and thus the best profile and consensus pattern) in DNA • More specifically, we want to maximize Score(s, DNA) by varying the starting positions si, where: si = [1, …, n-l+1] i = [1, …, t]

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Brute. Force. Motif. Search 1. Brute. Force. Motif. Search(DNA, t, n, l) 2. best. Score 0 3. for each s=(s 1, s 2, . . . , st) from (1, 1, . . . , 1) to (n-l+1, . . . , n-l+1) 4. if (Score(s, DNA) > best. Score) 5. best. Score(s, DNA) 6. best. Motif (s 1, s 2 , . . . , st) 7. return best. Motif

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Running Time of Brute. Force. Motif. Search • Varying among (n - l + 1) positions in each of the t sequences, we’re looking at (n - l + 1)t sets of starting positions • For each set of starting positions, the scoring function requires l operations, so the complexity is l (n – l + 1)t = O(l nt) • It means that for t = 8, n = 1000, l = 10 we must perform approximately 1020 computations – it will take billions of years

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info The Median String Problem • Given a set of t DNA sequences, find a pattern (string of length l ) that appears in all t sequences with the minimum number of mutations • This pattern (called a median string) will be the motif (i. e. , as its consensus)

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Hamming Distance • Hamming distance • d. H(v, w) is the number of nucleotide pairs that do not match when v and w are aligned. For example: d. H(AAAAAA, ACAAAC) = 2

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Total Distance: Definition • Given an l-mer v, for each DNA sequence i, compute all d. H(v, x), where x is an l-mer with some starting position si (1 < si < n – l + 1) • Find the minimum of d. H(v, x) among all l-mers x in sequence i. This is the Hamming distance between v and sequence i • Total. Distance(v, DNA) is the sum of the minimum Hamming distances for each DNA sequence i • Total. Distance(v, DNA) = mins d. H(v, s), where s is the set of starting positions s 1, s 2, …, st

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Total Distance: Example • Given v = “acgt” d. H(v, x) = 1 acgt cctgatagacgctatctggctatccacgtac. Ataggtcctctgtgcgaatctatgcgtttccaaccat acgt d. H(v, x) = 0 agtactggtgtacatttgatacgtacaccggcaacctgaaacgctcagaaccagaagtgc acgt aaa. Agt. Ccgtgcaccctcttcgtggctctggccaacgagggctgatgtataagacgaaaatttt acgt d. H(v, x) = 0 d. H(v, x) = 2 agcctccgatgtaagtcatagctgtaactattacctgccacccctattacatcttacgtataca acgt d. H(v, x) = 1 ctgttatacaacgcgtcatggcggggtatgcgttttggtcgtcgtacgctcgatcgttaacgta. Ggtc v is the sequence in red, x is the sequence in blue • Total. Distance(v, DNA) = 1+0+2+0+1 = 4

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info The Median String Problem: Formulation • Goal: Given a set of DNA sequences, find a median string with the minimum total distance • Input: A t x n matrix DNA, and l, the length of the motif to be found • Output: A string v of l nucleotides that minimizes Total. Distance(v, DNA) over all strings of that length

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Median String Search Algorithm 1. Median. String. Search (DNA, t, n, l) 2. best. Word AAA…A 3. best. Distance ∞ 4. for each l-mer v from AAA…A to TTT…T if Total. Distance(v, DNA) < best. Distance 5. best. Distance Total. Distance(v, DNA) 6. best. Word v 7. return best. Word Time complexity: O(l tn 4 l ).

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Motif Finding Problem == Median String Problem • The Motif Finding is a maximization problem while Median String is a minimization problem • One is sequence-based and the other pattern-based. • However, the Motif Finding problem and Median String problem are computationally equivalent • Need to show that minimizing Total. Distance is equivalent to maximizing Score, with the median string as the consensus string

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info We are looking for the same thing l a G g t a c T t C c A t a c g t T A g t a c g t C c A t C c g t a c g G _________ Alignment Profile A C G T 3 0 1 0 3 1 1 0 2 4 0 0 1 4 0 0 0 3 1 0 0 0 5 1 0 1 4 _________ Consensus a c g t Score 3+4+4+5+3+4 Total. Distance 2+1+1+0+2+1 Sum 5 5 5 5 t • At any column i Scorei + Total. Distancei = t • Because there are l columns Score + Total. Distance = l * t • Rearranging: Score = l * t - Total. Distance • l * t is constant and thus the minimization of the right side is equivalent to the maximization of the left side

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Motif Finding Problem vs. Median String Problem • Why bother reformulating the Motif Finding problem into the Median String problem? • The Motif Finding Problem needs to examine all the combinations of s. That is (n - l + 1)t combinations!!! • The Median String Problem needs to examine all 4 l combinations of v. This number is relatively smaller, usually

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Motif Finding: Improving the Running Time Recall Brute. Force. Motif. Search: 1. 2. 3. 4. 5. 6. 7. Brute. Force. Motif. Search(DNA, t, n, l) best. Score 0 for each s=(s 1, s 2, . . . , st) from (1, 1, . . . , 1) to (n-l+1, . . . , n-l+1) if (Score(s, DNA) > best. Score) best. Score(s, DNA) best. Motif (s 1, s 2 , . . . , st) return best. Motif

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Structuring the Search • How can we perform the line for each s=(s 1, s 2, . . . , st) from (1, 1, . . . , 1) to (n-l+1, . . . , n-l+1) ? • We need a method for efficiently structuring and navigating all possible motifs • This is the same as enumerating all t-digit numbers where each digit is in range {1, n-l+1}

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Median String: Improving the Running Time 1. Median. String. Search (DNA, t, n, l) 2. best. Word AAA…A 3. best. Distance ∞ 4. for each l-mer v from AAA…A to TTT…T if Total. Distance(v, DNA) < best. Distance 5. best. Distance Total. Distance(v, DNA) 6. best. Word v 7. return best. Word

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Structuring the Search • For the Median String Problem, we need to consider all 4 l possible l-mers (or l-digit l numbers): aa… aa aa… ac aa… ag aa… at. . tt… tt How to organize such a search?

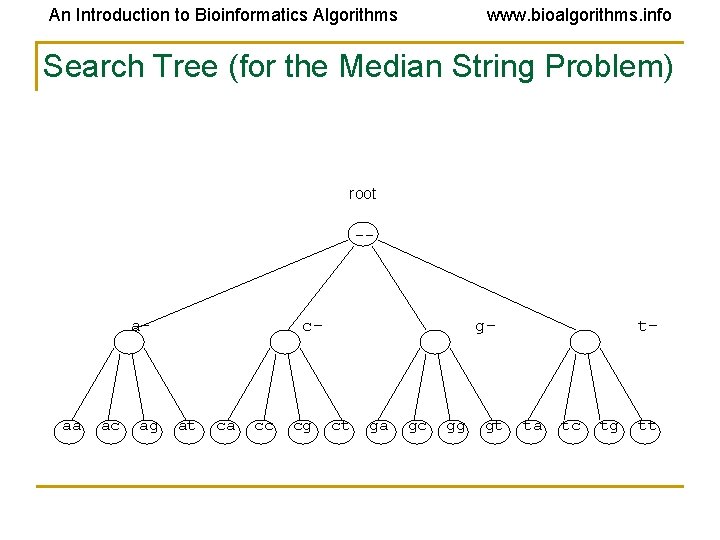
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Search Tree (for the Median String Problem) root -- a- aa ac ag c- at ca cc cg g- ct ga gc gg gt t- ta tc tg tt

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Analyzing the Search Tree • Characteristics of a search tree: • The (full) sequences are stored on its leaves • The parent sequence is a prefix of the sequences at its children • How can we move through the tree?

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Moving through the Search Tree • Four general moves in a search tree that we are about to consider: • Visit the next leaf (from left to right) • Visit all the leaves • Visit the next node (in DFS) • Bypass the children of a node (i. e. , pruning)

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Revisiting Brute. Force. Motif. Search 1. 2. 3. 4. 5. 6. 7. 8. 9. Brute. Force. Motif. Search. Again(DNA, t, n, l) s (1, 1, …, 1) best. Score(s, DNA) while forever s Next. Leaf (s, t, n-l+1) if (Score(s, DNA) > best. Score) best. Score(s, DNA) best. Motif (s 1, s 2, . . . , st) return best. Motif

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Can We Do Better in Motif Search? • Vector s = (s 1, s 2, …, st) may already have a weak profile from the first i instances (s 1, s 2, …, si) = (s, i) • Every new instance may add at most l to Score • Optimism: If all subsequent t-i instances (si+1, …st) add (t – i ) * l to Score(s, i, DNA) • If Score(s, i, DNA) + (t – i ) * l < Best. Score, it makes no sense to search the vertices of the subtree • Use By. Pass()

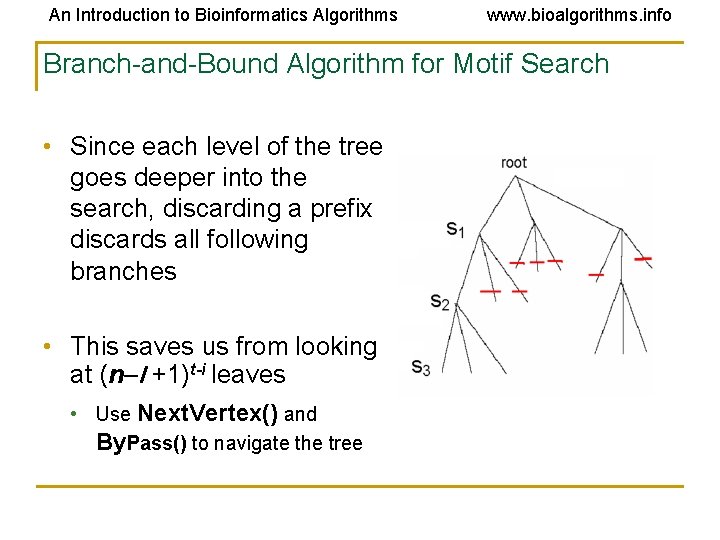
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Branch-and-Bound Algorithm for Motif Search • Since each level of the tree goes deeper into the search, discarding a prefix discards all following branches • This saves us from looking at (n–l +1)t-i leaves • Use Next. Vertex() and By. Pass() to navigate the tree

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Pseudocode for Branch-and-Bound Motif Search 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. Branch. And. Bound. Motif. Search(DNA, t, n, l) s (1, …, 1) // the leftmost (or first) leaf of the search tree best. Score 0 i 1 // (s, 1) = (1) represents the first child of the root of the search tree while i > 0 if i < t optimistic. Score(s, i, DNA) + (t – i )*l if optimistic. Score < best. Score (s, i) Bypass(s, i, t, n-l +1) else (s, i) Next. Vertex(s, i, t, n-l +1) else if Score(s, DNA) > best. Score(s) best. Motif (s 1, s 2, …, st) (s, i) Next. Vertex(s, i, t, n-l +1) return best. Motif

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Median String Search Improvements • Recall the computational difference between motif search and median string search • The Motif Finding Problem needs to examine all (n -l +1)t combinations of s • The Median String Problem needs to examine 4 l combinations of v. This number is relatively small • We want to use median string algorithm with the Branch-and-Bound trick as well

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Branch-and-Bound Applied to Median String Search • Note that if the total distance for a prefix is greater than that for the best word so far, Total. Distance (prefix, DNA) > Best. Distance then there is no use exploring the remaining part of the word • We can eliminate that branch and BYPASS exploring that branch further

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Bounded Median String Search 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. Branch. And. Bound. Median. String. Search(DNA, t, n, l ) s (1, …, 1) (or AA…A) // the leftmost leaf of the search tree best. Distance ∞ i 1 // (s, 1) = (1) = A represents the first child of the root while i > 0 if i < l prefix string corresponding to the first i nucleotides of s optimistic. Distance Total. Distance(prefix, DNA) if optimistic. Distance > best. Distance (s, i ) Bypass(s, i, l, 4) else (s, i ) Next. Vertex(s, i, l, 4) else word nucleotide string corresponding to s if Total. Distance(s, DNA) < best. Distance Total. Distance(word, DNA) best. Word word (s, i ) Next. Vertex(s, i, l, 4) return best. Word

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Improving the Bound • Given an l-mer w, divided into two parts at point i • u : prefix w 1, …, wi • v : suffix wi+1, . . . , wl • Find the minimum distance for u in each sequence • Calculate the Total. Distance for u • Note this doesn’t tell us anything about whether u is part of any motif. We only get a minimum distance for prefix u

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Improving the Bound (cont’d) • Repeating the process for the suffix v gives us a minimum distance for v • Since u and v are two (disjoint) substrings of w, we can assume that the minimum distance for u plus minimum distance for v can only be less than the minimum distance for w

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info A Better Bound (cont’d) • If d(prefix) + d(suffix) > best. Distance: • Motif w (prefix. suffix) cannot give a better (lower) distance than d(prefix) + d(suffix) • In this case, we can By. Pass()

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Better Bounded Median String Search 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. Improved. Branch. And. Bound. Median. String. Search(DNA, t, n, l) s = (1, 1, …, 1) (or AA…A) bestdistance = ∞; bestsubstring[1. . l] = ∞ i=1 while i > 0 if i < l prefix = nucleotide string corresponding to (s 1, s 2, …, si ) optimistic. Prefix. Distance = Total. Distance (prefix, DNA) if (optimistic. Prefix. Distance < bestsubstring[ i ]) bestsubstring[ i ] = optimistic. Prefix. Distance if (l - i < i ) optimistic. Sufx. Distance = bestsubstring[l -i ] else optimistic. Sufx. Distance = 0; if optimistic. Prefix. Distance + optimistic. Sufx. Distance > best. Distance (s, i ) = Bypass(s, i, l, 4) else (s, i ) = Next. Vertex(s, i, l, 4) else word = nucleotide string corresponding to (s 1, s 2, …, st) if Total. Distance( word, DNA) < best. Distance = Total. Distance(word, DNA) best. Word = word (s, i) = Next. Vertex(s, i, l, 4) return best. Word WRONG!

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Better Bounded Median String Search 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. Improved. Branch. And. Bound. Median. String. Search(DNA, t, n, l) s = (1, 1, …, 1) (or AA…A) bestdistance = ∞; bestsubstring[1. . l/2] = ∞ perform a BFS to calculate bestsubstring[1. . l/2] i=1 while i > 0 if i < l prefix = nucleotide string corresponding to (s 1, s 2, …, si ) optimistic. Prefix. Distance = Total. Distance (prefix, DNA) if (l - i < i ) optimistic. Sufx. Distance = bestsubstring[l -i ] else optimistic. Sufx. Distance = bestsubstring[l /2] ; if optimistic. Prefix. Distance + optimistic. Sufx. Distance > best. Distance (s, i ) = Bypass(s, i, l, 4) else (s, i ) = Next. Vertex(s, i, l, 4) else word = nucleotide string corresponding to (s 1, s 2, …, st) if Total. Distance( word, DNA) < best. Distance = Total. Distance(word, DNA) best. Word = word (s, i) = Next. Vertex(s, i, l, 4) return best. Word

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info More on the Motif Problem • Exhaustive Motif Search and Median String Search are both exact algorithms • They always find the optimal solution, though they may be too slow to perform practical tasks • Both problems are NP-hard • Many algorithms sacrifice optimality for speed. They are called heuristic algorithms.

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info CONSENSUS: Greedy Motif Search • Find two closest l-mers in sequences 1 and 2, and form a 2 x l alignment matrix with Score(s, 2, DNA) • At each of the following t-2 iterations CONSENSUS, find a “best” l-mer in sequence i from the perspective of the already constructed (i-1) x l alignment matrix for the first (i-1) sequences • In other words, it finds an l-mer in sequence i maximizing Score(s, i, DNA) under the assumption that the first (i-1) l-mers have been already chosen • CONSENSUS sacrifices optimal solution for speed: in fact the bulk of the time is actually spent locating the first 2 l-mers

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Some Motif Finding Programs • • CONSENSUS Hertz, Stormo (1989) • • Gibbs. DNA Lawrence et al (1993) • MULTIPROFILER Keich, Pevzner (2002) MITRA Eskin, Pevzner (2002) Pattern Branching Price, Pevzner (2003) • MEME Bailey, Elkan (1995) • Random. Projections • Sequence Weighting Buhler, Tompa (2002) Chen, Jiang (2006)

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info How to search a motif space? Start from random candidate motifs (seeds) Search motif space for the star

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Search small neighborhoods

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Exhaustive local search A lot of work, most of it unecessary

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Best Neighbor (of Pattern. Branching) Branch from the seed strings (motifs) Find best neighbor – of the highest score Don’t consider branches leading to scores not as good as the best score so far (called Hill Climbing)

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Scoring • Pattern. Branching uses total distance score (as in Median String Search) • For each sequence Si in the sample (DNA) S = {S 1, . . . , St}, let d(A, Si) = min{d(A, P) | P Si, |P| = |A|} • Then the total distance of A from the sample is d(A, S) = ∑ d(A, Si), Si S • For a pattern A, let D=Neighbor(A) be the set of patterns that differ from A in exactly 1 position. For convenience, add A to Neighbor(A). • We define Best. Neighbor(A) as the pattern B D=Neighbor(A) with lowest total distance d(B, S).

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Pattern. Branching Algorithm

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Pattern. Branching Performance • Pattern. Branching is faster than other patternbased algorithms • Motif Challenge Problem: • • sample of n = 20 sequences N = 600 nucleotides long implanted pattern of length l = 15 k = 4 mutations

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info PMS (Planted Motif Search) • Generate all possible l-mers from each input sequence Si. Let Ci be the collection of these l-mers. • Example: AAGTCAGGAGT Ci = 3 -mers: AAG AGT GTC TCA CAG AGG GGA GAG AGT

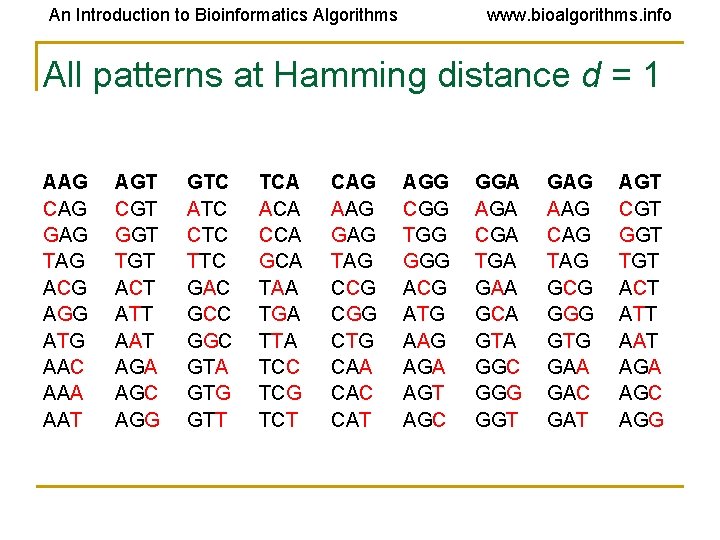
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info All patterns at Hamming distance d = 1 AAG CAG GAG TAG ACG AGG ATG AAC AAA AAT AGT CGT GGT TGT ACT ATT AAT AGA AGC AGG GTC ATC CTC TTC GAC GCC GGC GTA GTG GTT TCA ACA CCA GCA TAA TGA TTA TCC TCG TCT CAG AAG GAG TAG CCG CGG CTG CAA CAC CAT AGG CGG TGG GGG ACG ATG AAG AGA AGT AGC GGA AGA CGA TGA GAA GCA GTA GGC GGG GGT GAG AAG CAG TAG GCG GGG GTG GAA GAC GAT AGT CGT GGT TGT ACT ATT AAT AGA AGC AGG

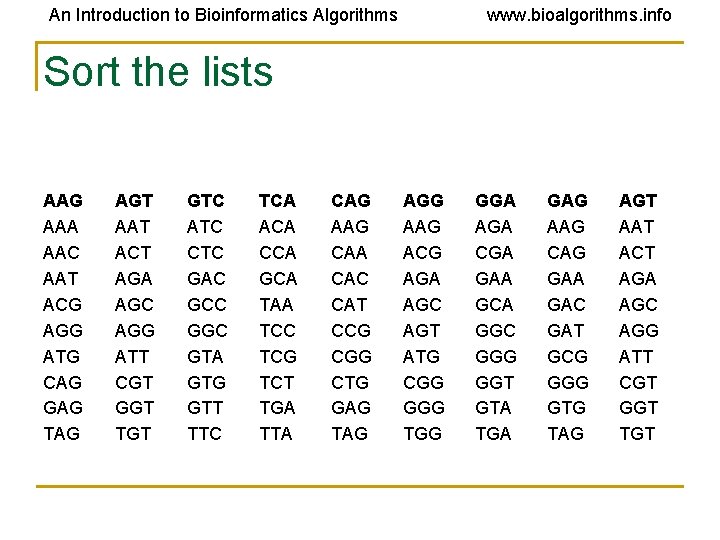
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Sort the lists AAG AAA AAC AAT ACG AGG ATG CAG GAG TAG AGT AAT ACT AGA AGC AGG ATT CGT GGT TGT GTC ATC CTC GAC GCC GGC GTA GTG GTT TTC TCA ACA CCA GCA TAA TCC TCG TCT TGA TTA CAG AAG CAA CAC CAT CCG CGG CTG GAG TAG AGG AAG ACG AGA AGC AGT ATG CGG GGG TGG GGA AGA CGA GAA GCA GGC GGG GGT GTA TGA GAG AAG CAG GAA GAC GAT GCG GGG GTG TAG AGT AAT ACT AGA AGC AGG ATT CGT GGT TGT

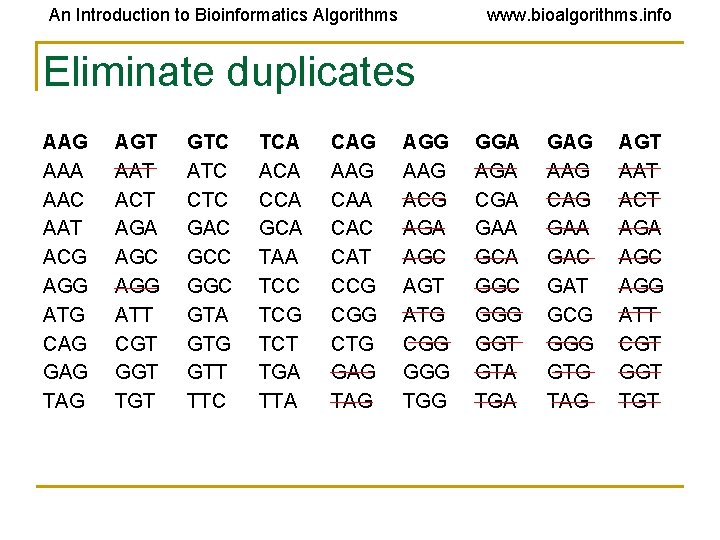
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Eliminate duplicates AAG AAA AAC AAT ACG AGG ATG CAG GAG TAG AGT AAT ACT AGA AGC AGG ATT CGT GGT TGT GTC ATC CTC GAC GCC GGC GTA GTG GTT TTC TCA ACA CCA GCA TAA TCC TCG TCT TGA TTA CAG AAG CAA CAC CAT CCG CGG CTG GAG TAG AGG AAG ACG AGA AGC AGT ATG CGG GGG TGG GGA AGA CGA GAA GCA GGC GGG GGT GTA TGA GAG AAG CAG GAA GAC GAT GCG GGG GTG TAG AGT AAT ACT AGA AGC AGG ATT CGT GGT TGT

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Find motif common to all lists • Follow this procedure for all sequences • Find a motif common to all Li (once duplicates have been eliminated) • This is the planted motif

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info PMS Running Time • It takes time to • Generate variants • Sort lists Here, m = length of sequence • Find and eliminate duplicates • Running time of this algorithm: w is the word length of the computer