An Introduction to Bioinformatics Algorithms www bioalgorithms info

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Dynamic Programming: Edit Distance

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Outline • • DNA Sequence Comparison: First Success Stories Change Problem Manhattan Tourist Problem Longest Paths in Graphs Sequence Alignment Edit Distance Longest Common Subsequence Problem Dot Matrices

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info DNA Sequence Comparison: First Success Story • Finding sequence similarities with genes of known function is a common approach to infer a newly sequenced gene’s function • In 1984 Russell Doolittle and colleagues found similarities between a cancercausing gene and the normal growth factor (PDGF) gene

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Cystic Fibrosis • • Cystic fibrosis (CF) is a chronic and frequently fatal disease of the body's mucus (abnormally high level of mucus in glands). CF primarily affects the respiratory systems in children. Mucus is a slimy material that coats many epithelial surfaces and is secreted into fluids such as saliva

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Cystic Fibrosis: Inheritance • In early 1980 s biologists hypothesized that CF is a genetic disorder caused by mutations in a gene that remained unknown till 1989 • Heterozygous carriers are asymptomatic • Must be homozygously recessive in this gene in order to be diagnosed with CF

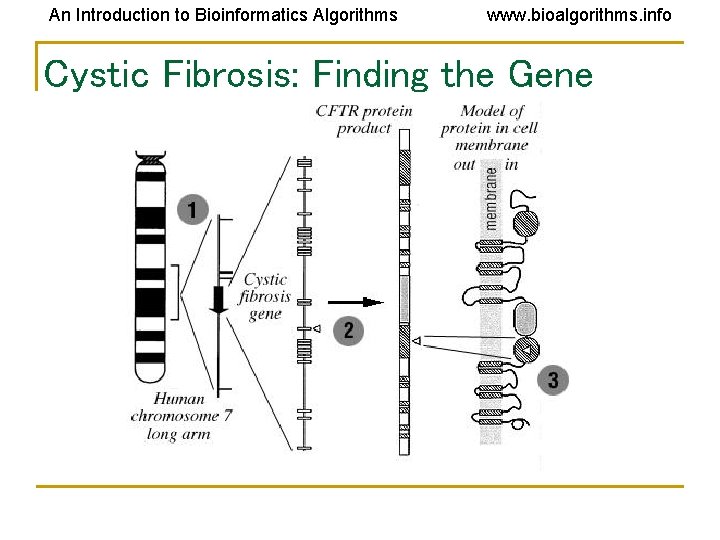
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Cystic Fibrosis: Finding the Gene

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Finding Similarities between the Cystic Fibrosis Gene and ATP binding proteins • ATP binding proteins are present on cell membrane and act as transport channel (ATP – Adenosine Trypho. Phate – is the energy of the cell) • In 1989 biologists found similarity between the cystic fibrosis gene and ATP binding proteins • A plausible function for cystic fibrosis gene, given the fact that CF involves sweet secretion with abnormally high sodium level

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Cystic Fibrosis: Mutation Analysis If a high % of cystic fibrosis (CF) patients have a certain mutation in the gene and the normal patients don’t, then that could be an indicator of a mutation that is related to CF A certain mutation was found in 70% of CF patients, convincing evidence that it is a predominant genetic diagnostics marker for CF

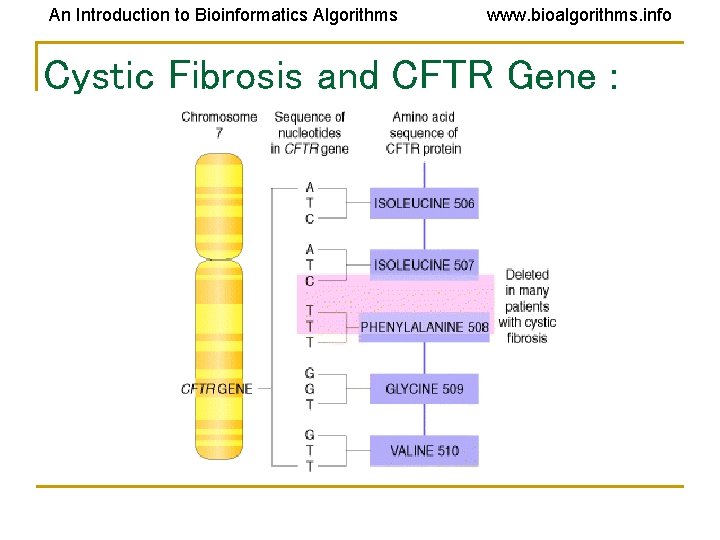
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Cystic Fibrosis and CFTR Gene :

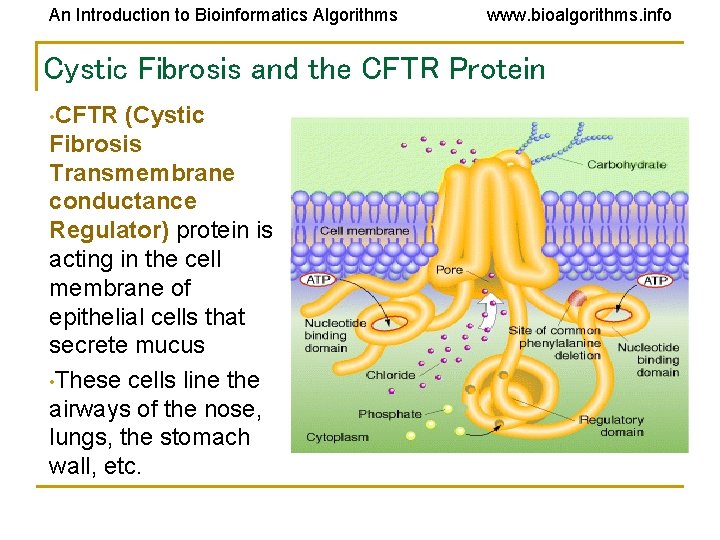
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Cystic Fibrosis and the CFTR Protein • CFTR (Cystic Fibrosis Transmembrane conductance Regulator) protein is acting in the cell membrane of epithelial cells that secrete mucus • These cells line the airways of the nose, lungs, the stomach wall, etc.

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Mechanism of Cystic Fibrosis • • The CFTR protein (1480 amino acids) regulates a chloride ion channel Adjusts the “wateriness” of fluids secreted by the cell Those with cystic fibrosis are missing a single amino acid in their CFTR Mucus ends up being too thick, affecting many organs

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Bring in the Bioinformaticians • • Similarities between a gene with known function and a gene with unknown function allow biologists to infer the function of the gene Computing a similarity score between two genes tells how likely it is that they have similar functions Dynamic programming is a technique for revealing similarities between sequences The Change Problem is a good problem to introduce the idea of dynamic programming

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info The Change Problem Goal: Convert some amount of money M into given denominations, using the fewest possible number of coins Input: An amount of money M, and an array of d denominations c = (c 1, c 2, …, cd), in a decreasing order of value (c 1 > c 2 > … > cd) Output: A list of d integers i 1, i 2, …, id such that c 1 i 1 + c 2 i 2 + … + c d id = M and i 1 + i 2 + … + id is minimal

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Change Problem: Example Given the denominations 1, 3, and 5, what is the minimum number of coins needed to make change for a given value? Value Min # of coins 1 2 3 4 5 6 7 8 9 10 1 1 1 Only one coin is needed to make change for the values 1, 3, and 5

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Change Problem: Example (cont’d) Given the denominations 1, 3, and 5, what is the minimum number of coins needed to make change for a given value? Value Min # of coins 1 2 3 4 5 6 7 8 9 10 1 2 1 2 2 2 However, two coins are needed to make change for the values 2, 4, 6, 8, and 10.

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Change Problem: Example (cont’d) Given the denominations 1, 3, and 5, what is the minimum number of coins needed to make change for a given value? Value Min # of coins 1 2 3 4 5 6 7 8 9 10 1 2 1 2 3 2 Lastly, three coins are needed to make change for the values 7 and 9

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Change Problem: Recurrence This example is expressed by the following recurrence relation: min. Num. Coins(M-1) + 1 min. Num. Coins(M) = min of min. Num. Coins(M-3) + 1 min. Num. Coins(M-5) + 1

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Change Problem: Recurrence (cont’d) Given the denominations c: c 1, c 2, …, cd, the recurrence relation is: min. Num. Coins(M-c 1) + 1 min. Num. Coins(M) = of min. Num. Coins(M-c 2) + 1 … min. Num. Coins(M-cd) + 1

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Change Problem: A Recursive Algorithm 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Recursive. Change(M, c, d) if M = 0 return 0 best. Num. Coins infinity for i 1 to d if M ≥ ci num. Coins Recursive. Change(M – ci , c, d) if num. Coins + 1 < best. Num. Coins num. Coins + 1 return best. Num. Coins

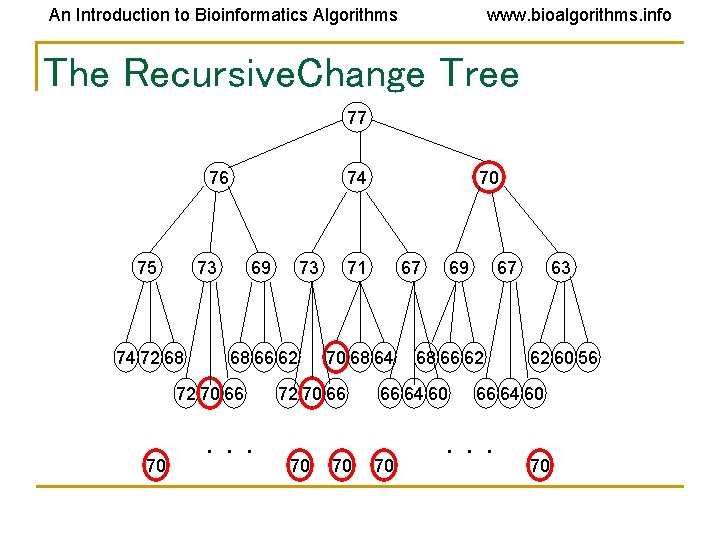
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info The Recursive. Change Tree 77 76 75 74 73 74 72 68 69 68 66 62 72 70 66 70 73 . . . 71 67 70 68 64 72 70 66 70 70 70 69 68 66 62 66 64 60 70 67 63 62 60 56 66 64 60 . . . 70

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Recursive. Change Is Not Efficient • It recalculates the optimal coin combination for a given amount of money repeatedly • i. e. , M = 77, c = (1, 3, 7): • Optimal coin combo for 70 cents is computed 9 times!

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Recursive. Change Is Not Efficient • It recalculates the optimal coin combination for a given amount of money repeatedly • i. e. , M = 77, c = (1, 3, 7): • Optimal coin combo for 70 cents is computed 9 times! • Optimal coin combo for 50 cents is computed billions of times!

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info We Can Do Better • We’re re-computing values in our algorithm more than once • Save results of each computation for 0 to M • This way, we can do a reference call to find an already computed value, instead of re-computing each time • Running time M*d, where M is the amount of money and d is the number of denominations

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info The Change Problem: Dynamic Programming 1. 2. 3. 4. 5. 6. 7. 8. 9. DPChange(M, c, d) best. Num. Coins 0 0 for m 1 to M best. Num. Coinsm infinity for i 1 to d if m ≥ ci if best. Num. Coinsm – ci+ 1 < best. Num. Coinsm – ci+ 1 return best. Num. Coins. M

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info DPChange: Example 0 0 1 2 3 4 5 6 0 0 0 1 0 2 1 2 0 1 1 3 2 2 2 1 2 3 2 1 2 0 1 2 3 4 5 6 7 8 9 1 0 2 0 1 2 3 4 5 0 2 1 0 1 2 3 4 5 6 7 8 0 1 2 3 0 2 0 1 2 3 4 5 6 7 1 0 1 2 0 1 1 2 3 2 1 2 3 c = (1, 3, 7) M = 9

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Manhattan Tourist Problem (MTP) Imagine seeking a path (from source to sink) to travel (only eastward and southward) with the most number of attractions (*) in the Manhattan grid Source * * *Sink

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Manhattan Tourist Problem (MTP) Imagine seeking a path (from source to sink) to travel (only eastward and southward) with the most number of attractions (*) in the Manhattan grid Source * * *Sink

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Manhattan Tourist Problem: Formulation Goal: Find the longest path in a weighted grid. Input: A weighted grid G with two distinct vertices, one labeled “source” and the other labeled “sink” Output: A longest path in G from “source” to “sink”

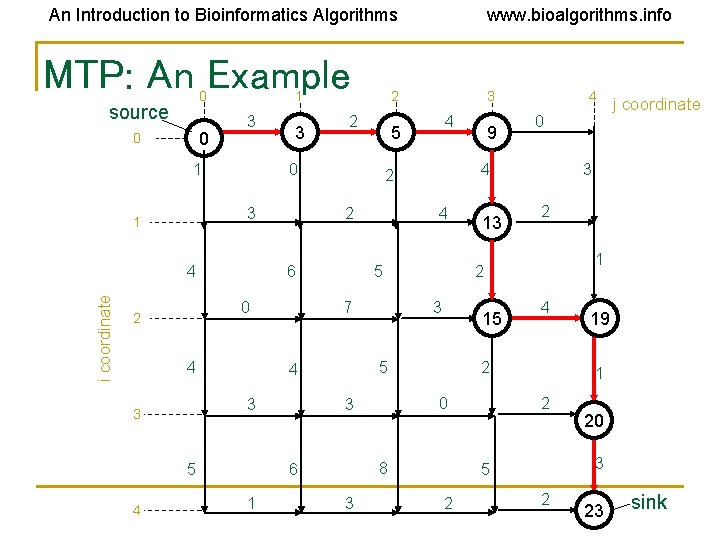
An Introduction to Bioinformatics Algorithms MTP: An Example 0 source 0 0 1 3 1 i coordinate 4 1 4 3 15 2 1 4 19 1 2 20 3 5 2 j coordinate 3 2 8 3 13 0 2 5 6 9 4 4 5 4 2 7 3 3 5 2 0 3 2 6 4 2 2 0 3 1 4 3 www. bioalgorithms. info 2 23 sink

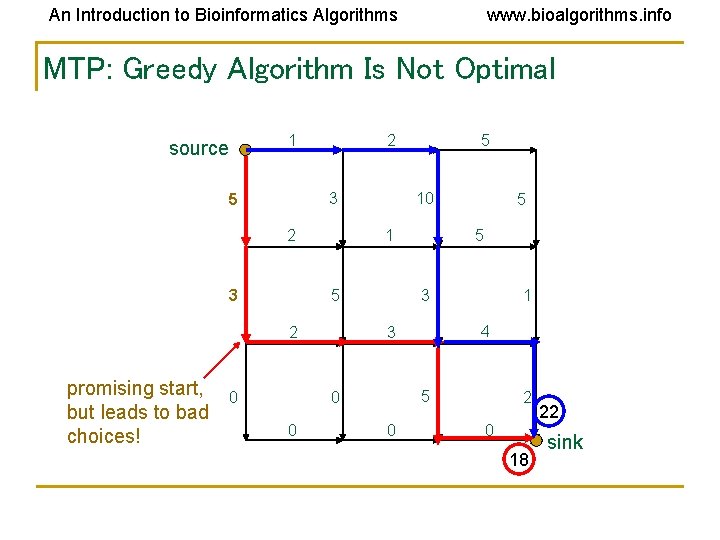
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info MTP: Greedy Algorithm Is Not Optimal source 1 2 3 5 2 3 10 5 3 1 4 3 5 0 0 5 5 1 2 promising start, 0 but leads to bad choices! 5 0 2 0 18 22 sink

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info MTP: Simple Program MT(n, m) if n=0 or m=0 return MT(n, m) x MT(n-1, m)+ length of the edge from (n- 1, m) to (n, m) y MT(n, m-1)+ length of the edge from (n, m-1) to (n, m) return max{x, y}

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info MTP: Simple Recursive Program MT(n, m) x MT(n-1, m)+ length of the edge from (n- 1, m) to (n, m) y MT(n, m-1)+ length of the edge from (n, m-1) to (n, m) return min{x, y} What’s wrong with this approach?

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info MTP: Dynamic Programming j 0 source 1 0 i 1 1 S 0, 1 = 1 5 S 1, 0 = 5 • Calculate optimal path score for each vertex in the graph • Each vertex’s score is the maximum of the prior vertex’ score plus the weight of the respective edge

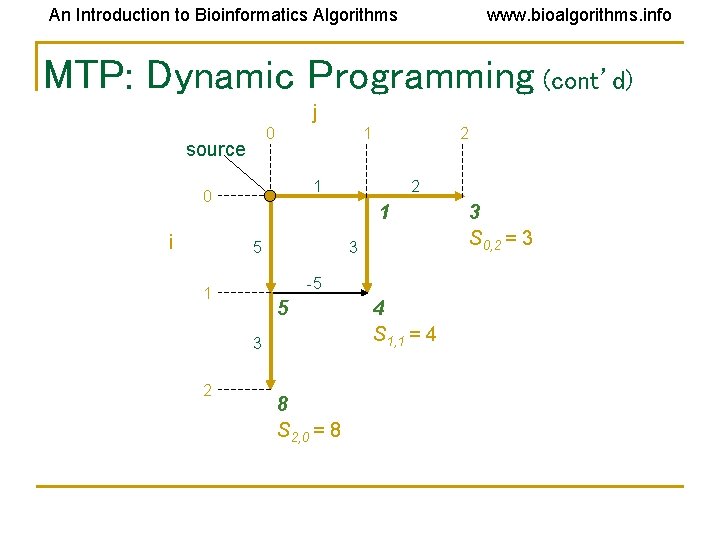
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info MTP: Dynamic Programming (cont’d) j 0 source 1 1 0 i 2 1 5 3 -5 1 5 3 2 2 8 S 2, 0 = 8 4 S 1, 1 = 4 3 S 0, 2 = 3

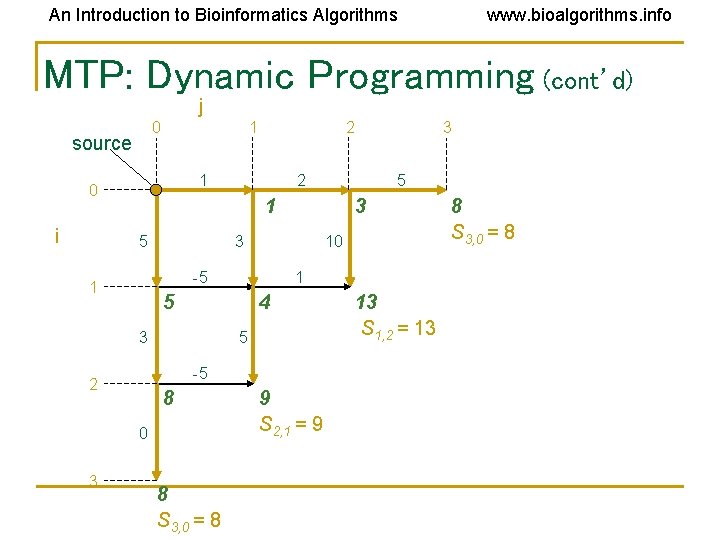
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info MTP: Dynamic Programming (cont’d) j 0 source 1 1 0 i 5 3 3 10 -5 1 1 5 4 5 3 -5 2 8 0 8 S 3, 0 = 8 3 2 1 5 3 2 9 S 2, 1 = 9 13 S 1, 2 = 13 8 S 3, 0 = 8

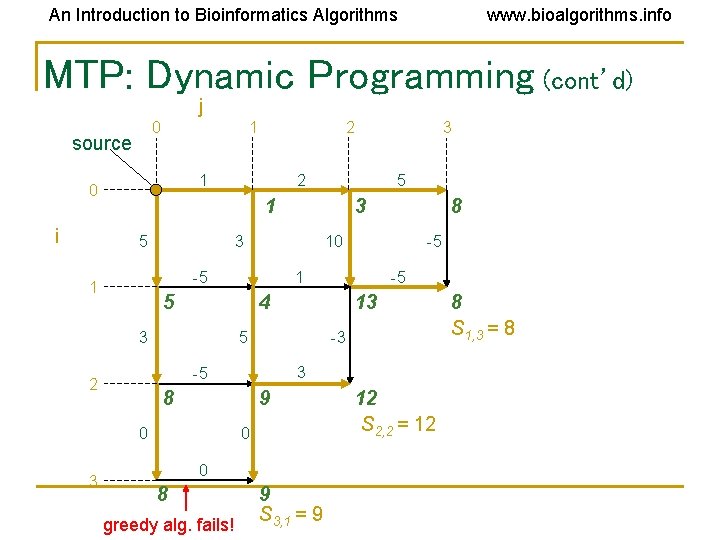
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info MTP: Dynamic Programming (cont’d) j 0 source 1 1 0 i 5 13 5 -3 3 -5 8 9 0 0 0 8 greedy alg. fails! -5 -5 4 3 8 10 1 5 2 3 3 -5 1 3 2 1 5 3 2 9 S 3, 1 = 9 12 S 2, 2 = 12 8 S 1, 3 = 8

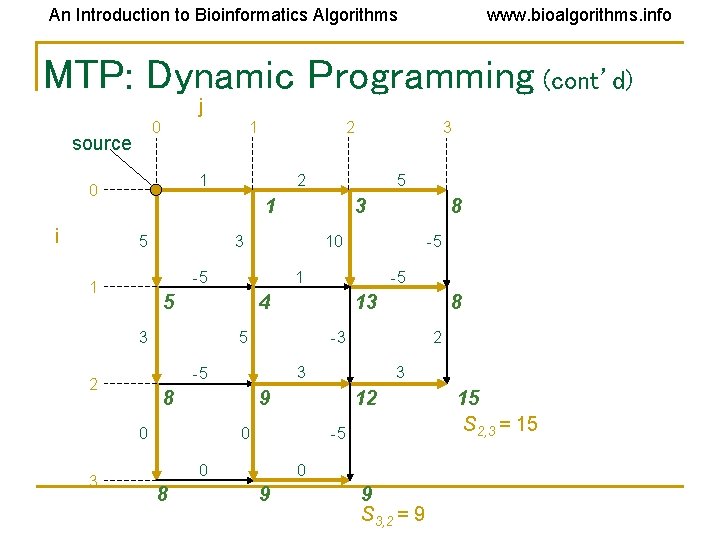
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info MTP: Dynamic Programming (cont’d) j 0 source 1 1 0 i 5 13 5 3 9 12 0 -5 0 8 2 3 8 8 -3 -5 0 -5 -5 4 3 8 10 1 5 2 3 3 -5 1 3 2 1 5 3 2 0 9 9 S 3, 2 = 9 15 S 2, 3 = 15

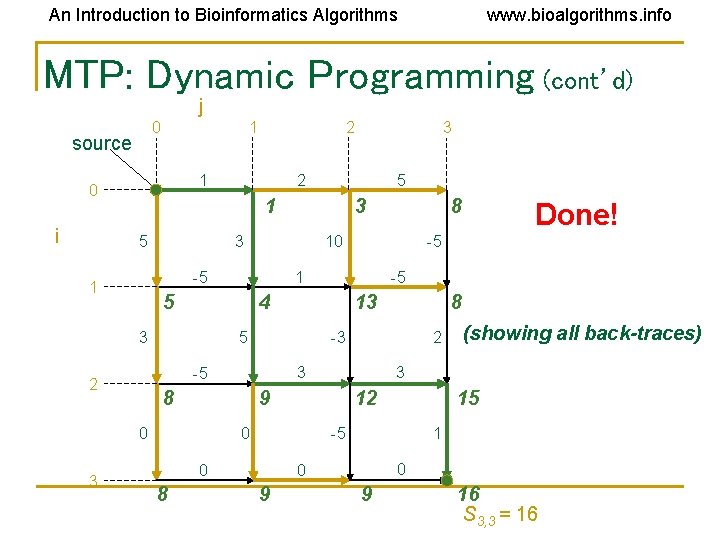
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info MTP: Dynamic Programming (cont’d) j 0 source 1 1 0 i 5 12 15 -5 0 1 0 0 9 (showing all back-traces) 3 9 0 8 2 3 8 8 -3 -5 0 -5 13 5 Done! -5 4 3 8 10 1 5 2 3 3 -5 1 3 2 1 5 3 2 9 16 S 3, 3 = 16

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info MTP: Recurrence Computing the score for a point (i, j) by the recurrence relation: si, j = max si-1, j + weight of the edge between (i-1, j) and (i, j) si, j-1 + weight of the edge between (i, j-1) and (i, j) The running time is n x m for a n by m grid (n = # of rows, m = # of columns)

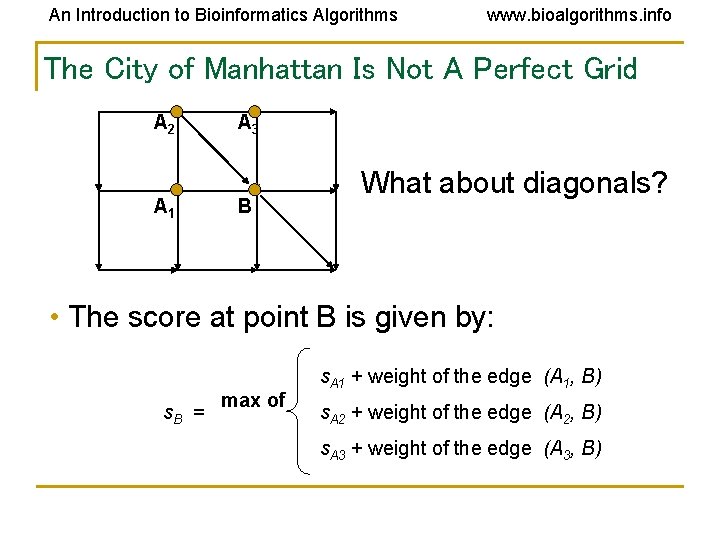
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info The City of Manhattan Is Not A Perfect Grid A 2 A 1 A 3 B What about diagonals? • The score at point B is given by: s. B = max of s. A 1 + weight of the edge (A 1, B) s. A 2 + weight of the edge (A 2, B) s. A 3 + weight of the edge (A 3, B)

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Traveling in an Arbitrary Graph Computing the score for point x is given by the recurrence relation: sx = max sy + weight of vertex (y, x) where of y є Predecessors(x) • Predecessors (x) – set of vertices that have edges leading to x • The running time for a graph with E edges is …?

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Traveling in an Arbitrary Graph Computing the score for point x is given by the recurrence relation: sx = max sy + weight of vertex (y, x) where of y є Predecessors(x) • Predecessors (x) – set of vertices that have edges leading to x • The running time for a graph with E edges is O(E) since each edge is evaluated once

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Traveling in a Graph • The only hitch is that one must decide on the order in which visit the vertices • By the time the vertex x is analyzed, the values sy for all its predecessors y should be computed • We need to traverse the vertices in some order • Try to find such order for a directed cycle ? ? ?

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info DAG: Directed Acyclic Graph • • Since Manhattan is not a perfect regular grid, we represent it as a DAG for Dressing in the morning problem

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Topological Ordering • • A labeling of vertices of the graph is called topological ordering of the DAG if every edge of the DAG connects a vertex with a smaller label to a vertex with a larger label In other words, if vertices are positioned on a line in an increasing order of labels then all edges go from left to right.

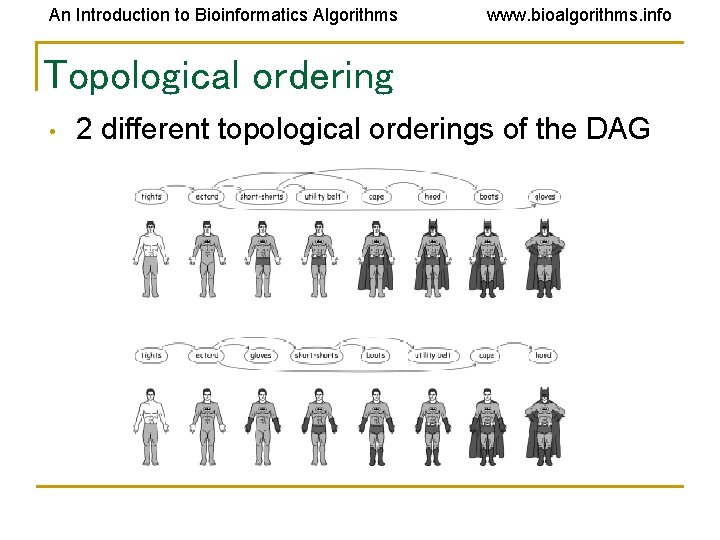
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Topological ordering • 2 different topological orderings of the DAG

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Longest Path in DAG Problem • Goal: Find a longest path between two vertices in a weighted DAG • Input: A weighted DAG G with source and sink vertices • Output: A longest path in G from source to sink

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Longest Path in a DAG: Dynamic Programming • • Suppose vertex v has indegree 3 and predecessors {u 1, u 2, u 3} Longest path to v from source is: su 1 + weight of edge from u 1 to v sv = max of su 2 + weight of edge from u 2 to v su 3 + weight of edge from u 3 to v In General: sv = maxu (su + weight of edge from u to v)

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Traversing the Manhattan Grid • 3 different strategies: • a) Column by column • b) Row by row • c) Along diagonals a) c) b)

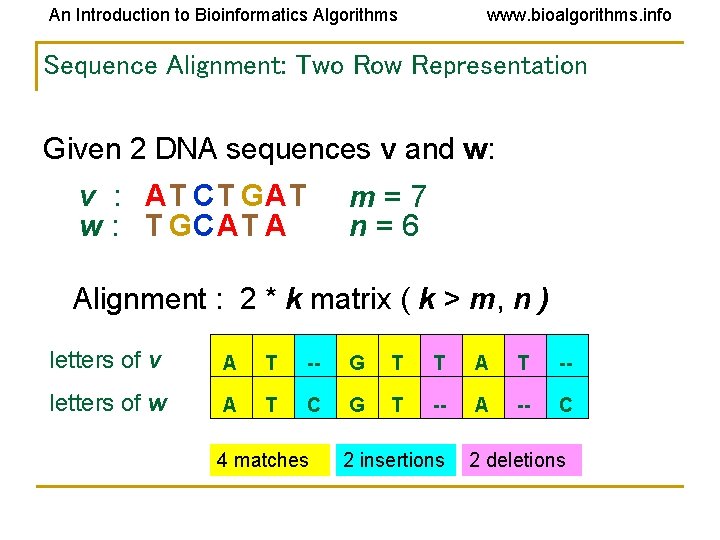
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Sequence Alignment: Two Row Representation Given 2 DNA sequences v and w: v : AT CT GAT w : T GCAT A m = 7 n = 6 Alignment : 2 * k matrix ( k > m, n ) letters of v A T -- G T T A T -- letters of w A T C G T -- A -- C 4 matches 2 insertions 2 deletions

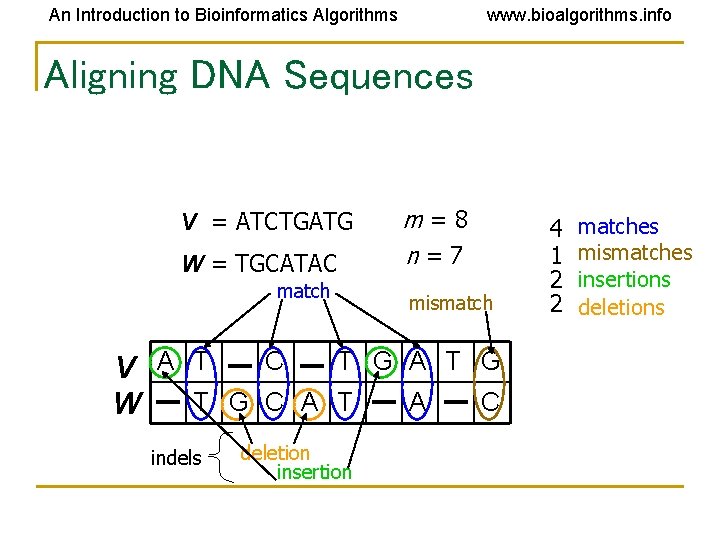
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Aligning DNA Sequences V = ATCTGATG W = TGCATAC match m=8 n=7 mismatch C T G A T G V A T T G C A T A C W indels deletion insertion 4 1 2 2 matches mismatches insertions deletions

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Common Subsequence – Alignment without Mismatches • Given two sequences v = v 1 v 2…vm and w = w 1 w 2…wn • The Common Subsequence of v and w is a sequence of positions in v: 1 < i 2 < … < it < m and a sequence of positions in w: 1 < j 2 < … < jt < n such that it -th letter of v equals to jt-letter of w

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Common Subsequence: Example 0 1 2 2 3 3 4 5 6 7 8 elements of v A T -- C -- T G A T C elements of w -- T 1 G C 2 3 A 4 T 5 -- -- C 7 i coords: j coords: 0 0 5 A 6 6 (0, 0) (1, 0) (2, 1) (2, 2) (3, 3) (3, 4) (4, 5) (5, 5) (6, 6) (7, 6) (8, 7) Matches shown in red positions in v: 2 < 3 < 4 < 6 < 8 positions in w: 1 < 3 < 5 < 6 < 7 Every common subsequence is a path in 2 -D grid

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Longest Common Subsequence – “Good” Alignment without Mismatches • Given two sequences v = v 1 v 2…vm and w = w 1 w 2…wn • The Longest Common Subsequence (LCS) of v and w is a sequence of positions in v: 1 < i 2 < … < i. T < m and a sequence of positions in w: 1 < j 2 < … < j. T < n such that it -th letter of v equals to jt-letter of w AND T is maximal

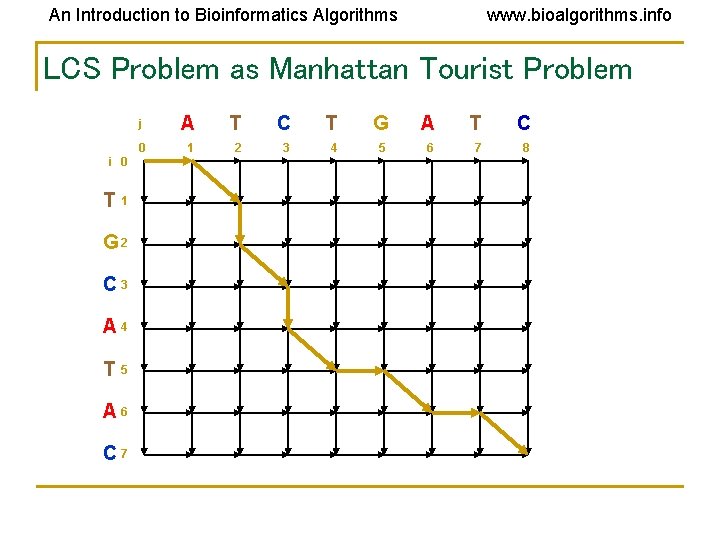
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info LCS Problem as Manhattan Tourist Problem i 0 T 1 G 2 C 3 A 4 T 5 A 6 C 7 j A T C T G A T C 0 1 2 3 4 5 6 7 8

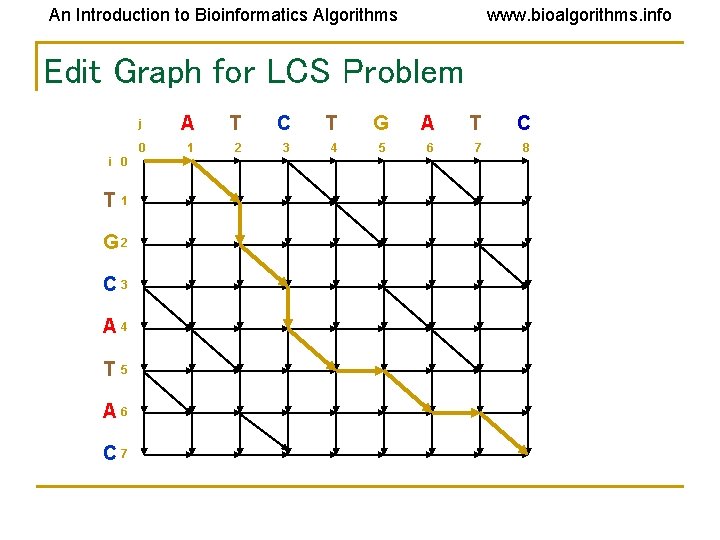
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Edit Graph for LCS Problem i 0 T 1 G 2 C 3 A 4 T 5 A 6 C 7 j A T C T G A T C 0 1 2 3 4 5 6 7 8

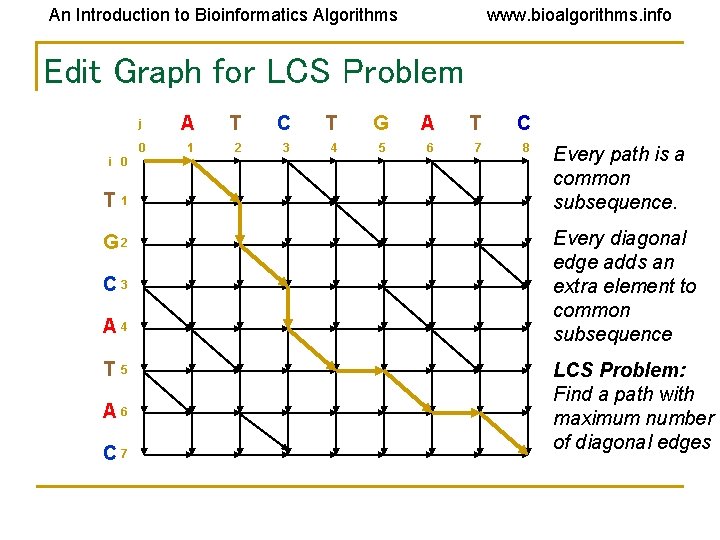
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Edit Graph for LCS Problem i 0 T 1 G 2 C 3 A 4 T 5 A 6 C 7 j A T C T G A T C 0 1 2 3 4 5 6 7 8 Every path is a common subsequence. Every diagonal edge adds an extra element to common subsequence LCS Problem: Find a path with maximum number of diagonal edges

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Computing LCS Let vi = prefix of v of length i: v 1 … vi and wj = prefix of w of length j: w 1 … wj The length of LCS(vi, wj) is computed by: si, j = max si-1, j si, j-1 si-1, j-1 + 1 if vi = wj

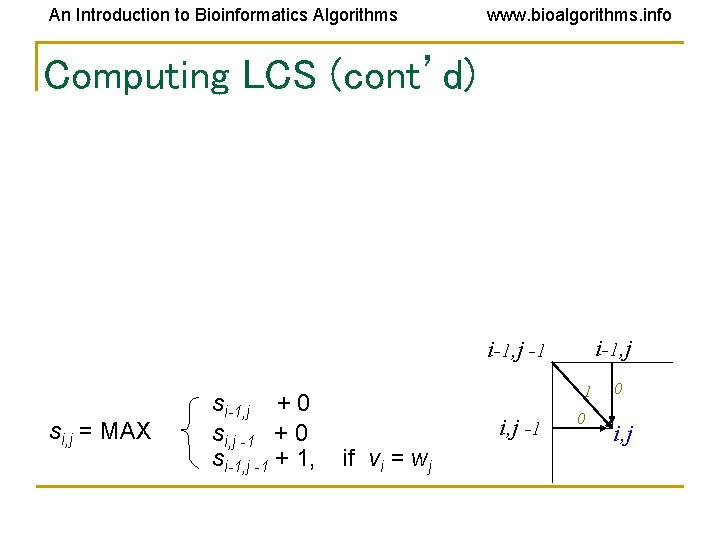
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Computing LCS (cont’d) i-1, j -1 si, j = MAX si-1, j + 0 si, j -1 + 0 si-1, j -1 + 1, if vi = wj 1 i, j -1 0 0 i, j

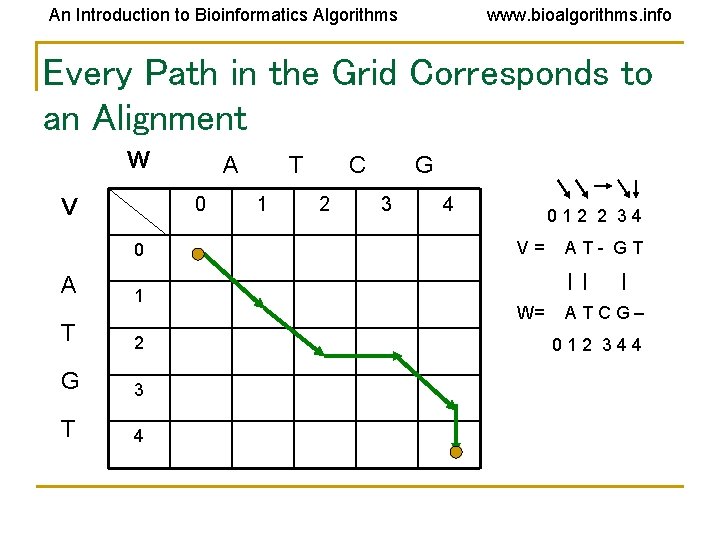
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Every Path in the Grid Corresponds to an Alignment W 0 V 0 A A 1 T 2 G 3 T 4 T 1 C 2 G 3 4 0 1 2 2 3 4 V = A T - G T | | | W= A T C G – 0 1 2 3 4 4

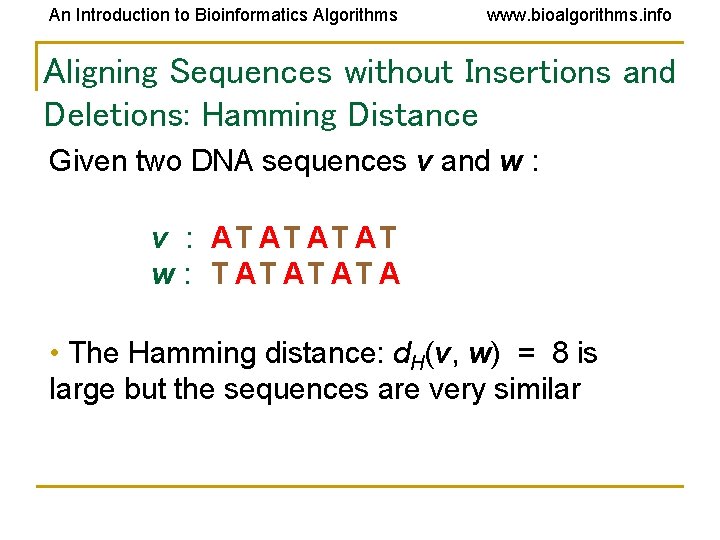
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Aligning Sequences without Insertions and Deletions: Hamming Distance Given two DNA sequences v and w : v : AT AT w : T AT A • The Hamming distance: d. H(v, w) = 8 is large but the sequences are very similar

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Aligning Sequences with Insertions and Deletions By shifting one sequence over one position: v : AT AT -w : -- T AT A • The edit distance: d. H(v, w) = 2. • Hamming distance neglects insertions and deletions in DNA

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Edit Distance Levenshtein (1966) introduced the edit distance between two strings as the minimum number of elementary operations (insertions, deletions, and substitutions) to transform one string into the other d(v, w) = MIN number of elementary operations to transform v w

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Edit Distance vs Hamming Distance Hamming distance always compares i-th letter of v with i-th letter of w V = ATAT W = TATA Hamming distance: d(v, w)=8 Computing Hamming distance is a trivial task.

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Edit Distance vs Hamming Distance Hamming distance always compares i-th letter of v with i-th letter of w V = ATAT W = TATA Just one shift Make it all line up Edit distance may compare i-th letter of v with j-th letter of w V = - ATAT W = TATA Hamming distance: Edit distance: d(v, w)=8 d(v, w)=2 Computing Hamming distance Computing edit distance is a trivial task is a non-trivial task

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Edit Distance vs Hamming Distance Hamming distance always compares i-th letter of v with i-th letter of w Edit distance may compare i-th letter of v with j-th letter of w V = ATAT V = - ATAT W = TATATATA Hamming distance: Edit distance: d(v, w)=8 d(v, w)=2 (one insertion and one deletion) How to find what j goes with what i ? ? ?

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Edit Distance: Example TGCATAT ATCCGAT in 5 steps TGCATAT TGCATA TGCAT ATCCAT ATCCGAT (delete last T) (delete last A) (insert A at front) (substitute C for 3 rd G) (insert G before last A) (Done)

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Edit Distance: Example TGCATAT ATCCGAT in 5 steps TGCATAT (delete last T) TGCATA (delete last A) TGCAT (insert A at front) ATGCAT (substitute C for 3 rd G) ATCCAT (insert G before last A) ATCCGAT (Done) What is the edit distance? 5?

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Edit Distance: Example (cont’d) TGCATAT ATCCGAT in 4 steps TGCATAT (insert A at front) ATGCATAT (delete 6 th T) ATGCATA (substitute G for 5 th A) ATGCGTA (substitute C for 3 rd G) ATCCGAT (Done)

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Edit Distance: Example (cont’d) TGCATAT ATCCGAT in 4 steps TGCATAT (insert A at front) ATGCATAT (delete 6 th T) ATGCATA (substitute G for 5 th A) ATGCGTA (substitute C for 3 rd G) ATCCGAT (Done) Can it be done in 3 steps? ? ?

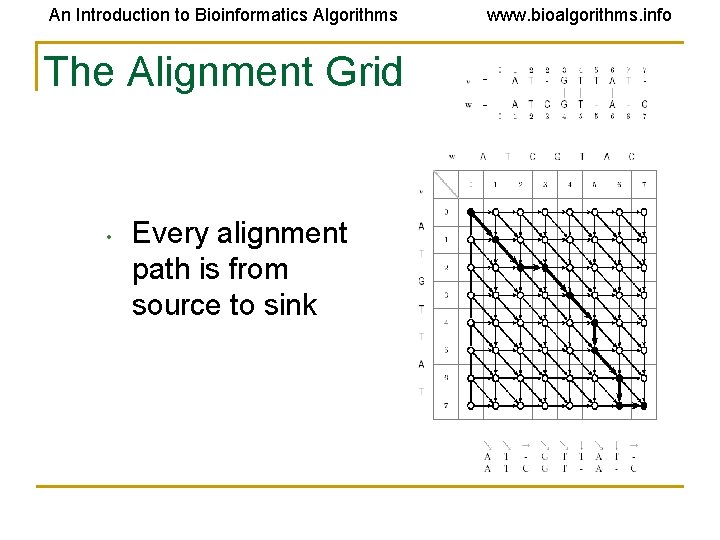
An Introduction to Bioinformatics Algorithms The Alignment Grid • Every alignment path is from source to sink www. bioalgorithms. info

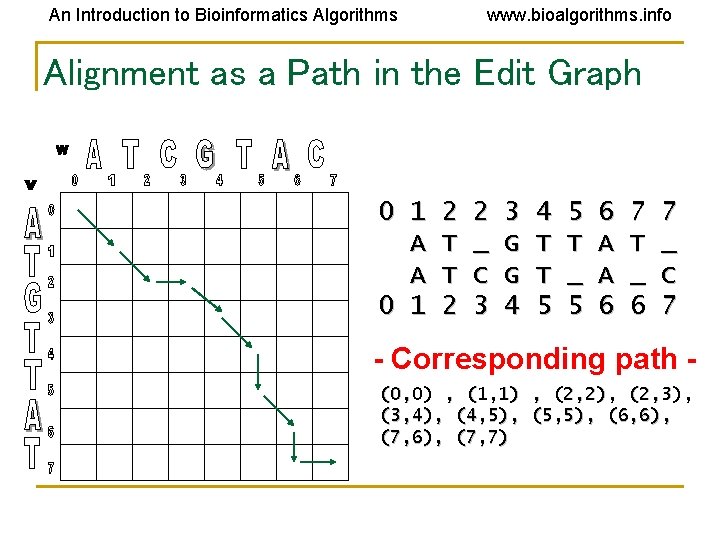
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Alignment as a Path in the Edit Graph 0 1 A A 0 1 2 T T 2 2 _ C 3 3 G G 4 4 T T 5 5 T _ 5 6 A A 6 7 T _ 6 7 _ C 7 - Corresponding path (0, 0) , (1, 1) , (2, 2), (2, 3), (3, 4), (4, 5), (5, 5), (6, 6), (7, 7)

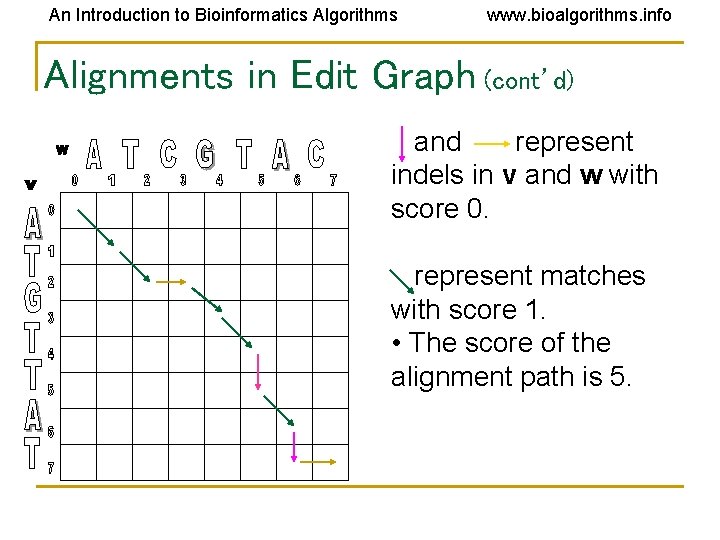
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Alignments in Edit Graph (cont’d) and represent indels in v and w with score 0. represent matches with score 1. • The score of the alignment path is 5.

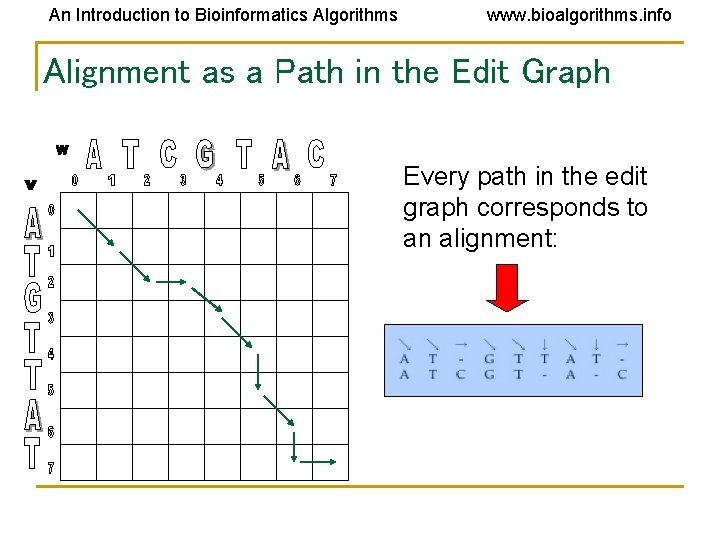
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Alignment as a Path in the Edit Graph Every path in the edit graph corresponds to an alignment:

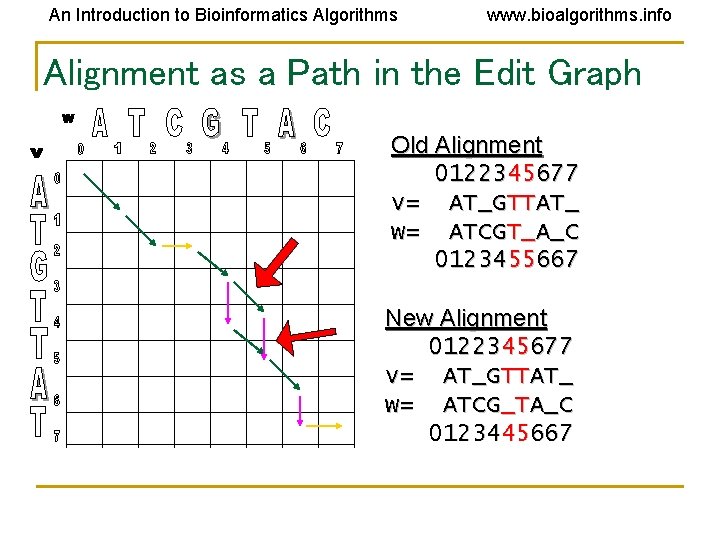
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Alignment as a Path in the Edit Graph Old Alignment 0122345677 v= AT_GTTAT_ w= ATCGT_A_C 0123455667 New Alignment 0122345677 v= AT_GTTAT_ w= ATCG_TA_C 0123445667

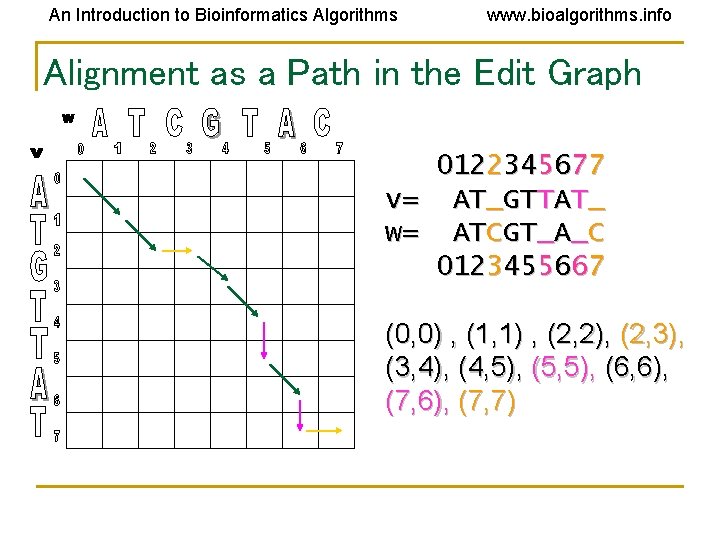
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Alignment as a Path in the Edit Graph 0122345677 v= AT_GTTAT_ w= ATCGT_A_C 0123455667 (0, 0) , (1, 1) , (2, 2), (2, 3), (3, 4), (4, 5), (5, 5), (6, 6), (7, 6), (7, 7)

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Alignment: Dynamic Programming si, j = si-1, j-1+1 if vi = wj max si-1, j si, j-1

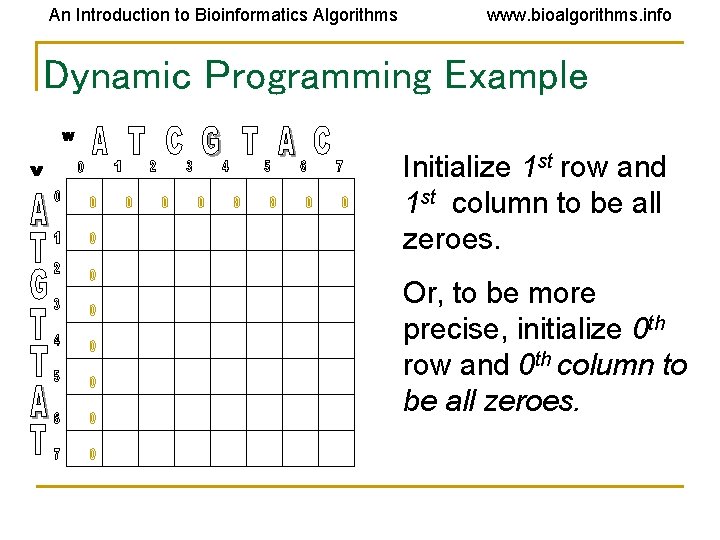
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Dynamic Programming Example Initialize 1 st row and 1 st column to be all zeroes. Or, to be more precise, initialize 0 th row and 0 th column to be all zeroes.

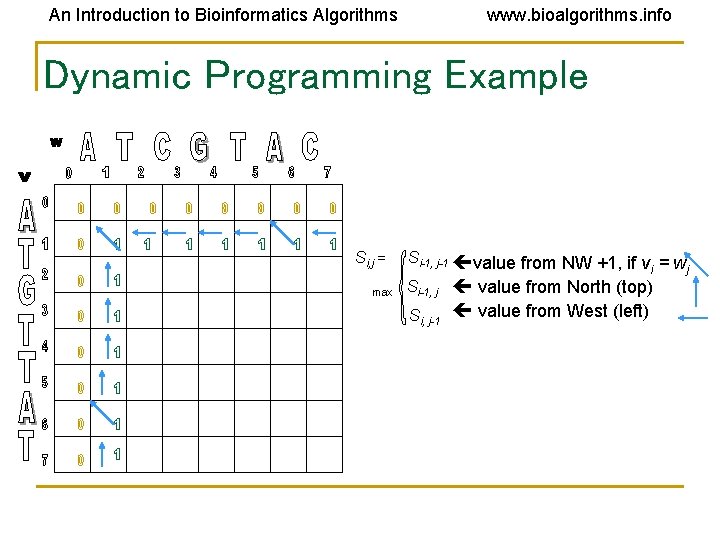
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Dynamic Programming Example Si, j = Si-1, j-1 value from NW +1, if v = w i j max Si-1, j value from North (top) Si, j-1 value from West (left)

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Alignment: Backtracking Arrows show where the score originated from. if from the top if from the left if vi = wj

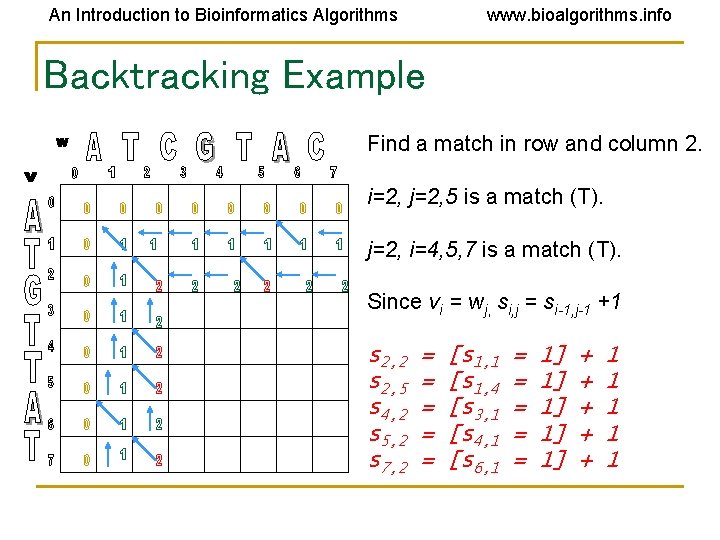
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Backtracking Example Find a match in row and column 2. i=2, j=2, 5 is a match (T). j=2, i=4, 5, 7 is a match (T). Since vi = wj, si, j = si-1, j-1 +1 s 2, 2 s 2, 5 s 4, 2 s 5, 2 s 7, 2 = = = [s 1, 1 [s 1, 4 [s 3, 1 [s 4, 1 [s 6, 1 = = = 1] 1] 1] + + + 1 1 1

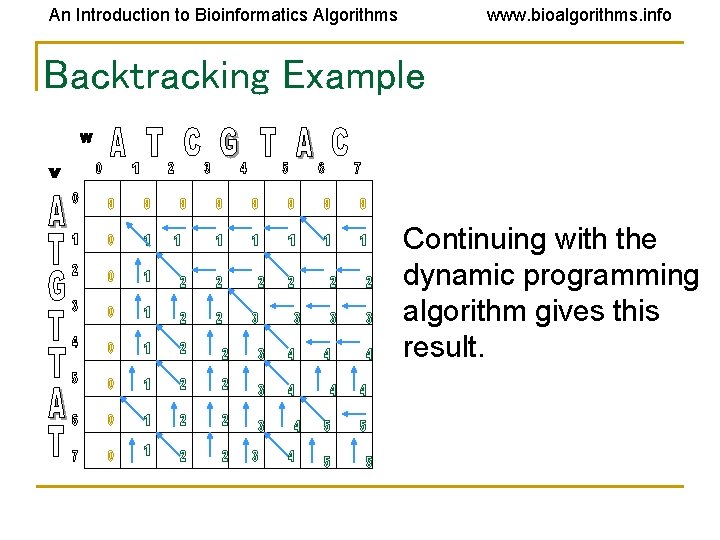
An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Backtracking Example Continuing with the dynamic programming algorithm gives this result.

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Alignment: Dynamic Programming si, j = si-1, j-1+1 if vi = wj max si-1, j si, j-1

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Alignment: Dynamic Programming si, j = si-1, j-1+1 if vi = wj max si-1, j+0 si, j-1+0 This recurrence corresponds to the Manhattan Tourist problem (three incoming edges into a vertex) with all horizontal and vertical edges weighted by zero.

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info LCS Algorithm 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. • • • LCS(v, w) for i 1 to n si, 0 0 for j 1 to m s 0, j 0 for i 1 to n for j 1 to m si-1, j si, j max si, j-1 si-1, j-1 + 1, if vi = wj “ “ if si, j = si-1, j bi, j “ “ if si, j = si, j-1 “ “ if si, j = si-1, j-1 + 1 return (sn, m, b)

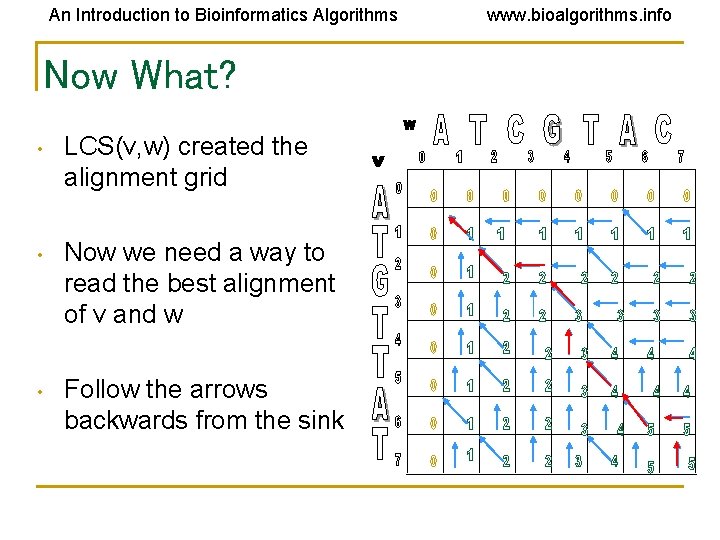
An Introduction to Bioinformatics Algorithms Now What? • LCS(v, w) created the alignment grid • Now we need a way to read the best alignment of v and w • Follow the arrows backwards from the sink www. bioalgorithms. info

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info Printing LCS: Backtracking 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. Print. LCS(b, v, i, j) if i = 0 or j = 0 return if bi, j = “ “ Print. LCS(b, v, i-1, j-1) print vi else if bi, j = “ “ Print. LCS(b, v, i-1, j) else Print. LCS(b, v, i, j-1)

An Introduction to Bioinformatics Algorithms www. bioalgorithms. info LCS Runtime • It takes O(nm) time to fill in the nxm dynamic programming matrix: the pseudocode consists of a nested “for” loop inside of another “for” loop.