An Introduction to Bioinformatics 2 Comparing biological sequences

An Introduction to Bioinformatics 2. Comparing biological sequences: sequence alignment

An Introduction to Bioinformatics DNA Sequence Comparison: First Success Story • Finding sequence similarities with genes of known function is a common approach to infer a newly sequenced gene’s function • In 1984 Russell Doolittle and colleagues found similarities between cancer-causing gene (v-sys in Simian Sarcoma Virus) and normal growth factor (PDGF) gene

An Introduction to Bioinformatics So what? • Identifying the similarity between PDGF and the viral oncogene helped lead to a modern hypothesis of cancer. • Identifying the similarity between ATP binding ion channels and the Cystic Fibrosis gene led to a modern hypothesis of CF. • Comparing sequences can yield biological insight. 3

An Introduction to Bioinformatics Similarity • Similar genes may have similar functions • Similar genes may have similar evolutionary origins • Similarity between sequences is not a vague idea--it can be quantified • But. . . how do we compute it?

An Introduction to Bioinformatics Complete DNA Sequences nearly 200 complete genomes have been sequenced 5

An Introduction to Bioinformatics Evolution 6

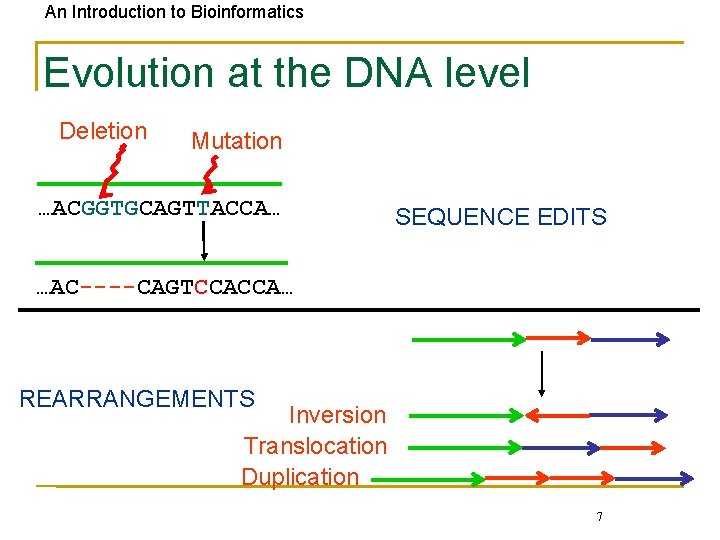
An Introduction to Bioinformatics Evolution at the DNA level Deletion Mutation …ACGGTGCAGTTACCA… SEQUENCE EDITS …AC----CAGTCCACCA… REARRANGEMENTS Inversion Translocation Duplication 7

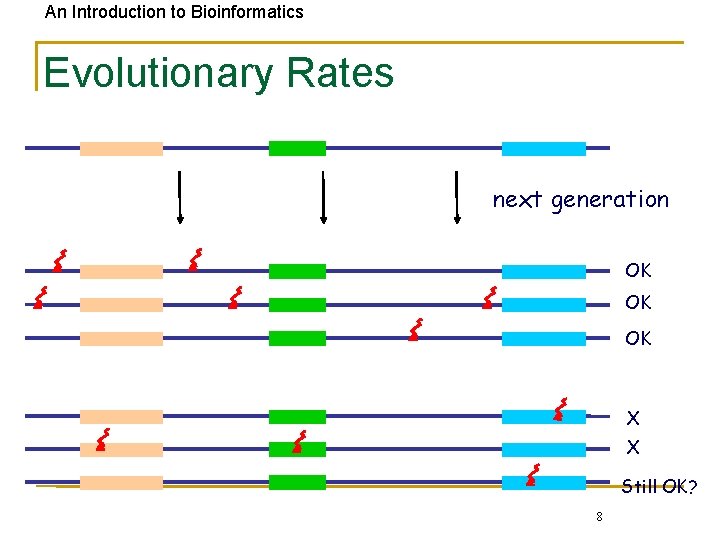
An Introduction to Bioinformatics Evolutionary Rates next generation OK OK OK X X Still OK? 8

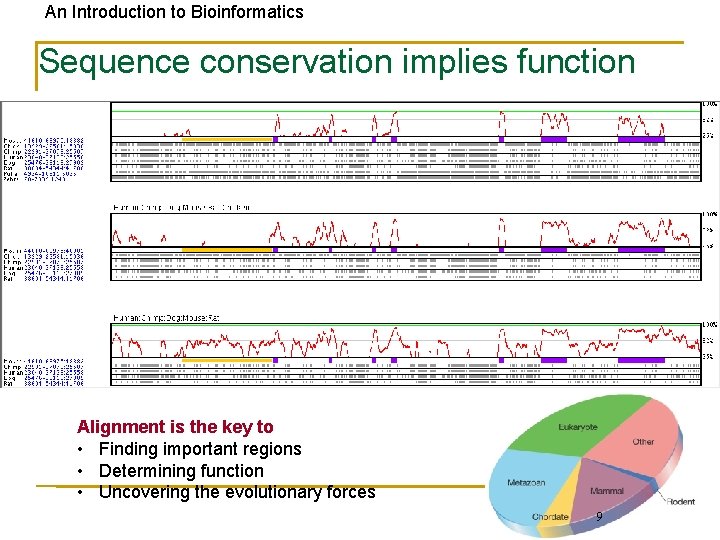
An Introduction to Bioinformatics Sequence conservation implies function Alignment is the key to • Finding important regions • Determining function • Uncovering the evolutionary forces 9

An Introduction to Bioinformatics Sequence Alignment AGGCTATCACCTGACCTCCAGGCCGATGCCC TAGCTATCACGACCGCGGTCGATTTGCCCGAC -AGGCTATCACCTGACCTCCAGGCCGA--TGCCC--TAG-CTATCAC--GACCGC--GGTCGATTTGCCCGAC Definition Given two strings x = x 1 x 2. . . x. M, y = y 1 y 2…y. N, an alignment is an assignment of gaps to positions 0, …, N in x, and 0, …, N in y, so as to line up each letter in one sequence with either a letter, or a gap in the other sequence 10

An Introduction to Bioinformatics Apologia for a diversion. . . • Computing similarity is detail-oriented, and we need to do some preliminary work first: • The Manhattan Tourist Problem introduces grids, graphs and edit graphs 11

An Introduction to Bioinformatics Manhattan Tourist Problem Where to? See the most stuff in the least time. 12

An Introduction to Bioinformatics Manhattan Tourist Problem (MTP) Imagine seeking a path (from source to sink) to travel (only eastward and southward) with the most number of attractions (*) in the Manhattan grid Source * * *Sink

An Introduction to Bioinformatics Manhattan Tourist Problem: Formulation Goal: Find the longest path in a weighted grid. Input: A weighted grid G with two distinct vertices, one labeled “source” and the other labeled “sink” Output: A longest path in G from “source” to “sink”

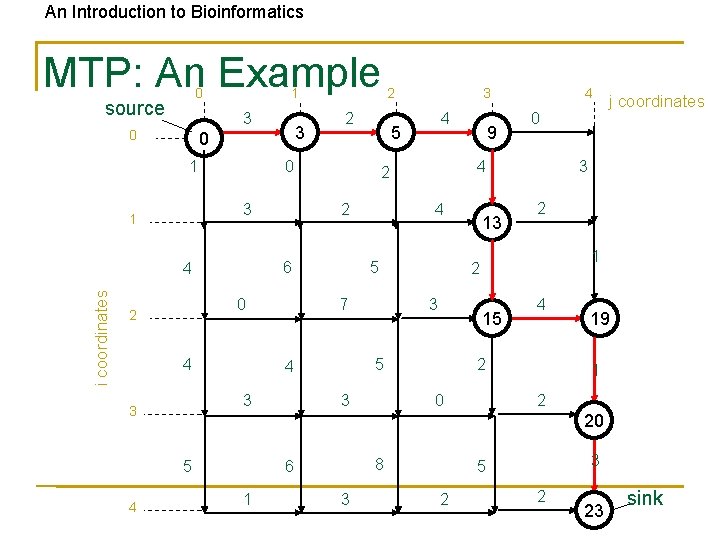
An Introduction to Bioinformatics MTP: An Example 0 source 1 3 0 1 i coordinates 4 0 13 2 1 15 5 j coordinates 3 2 3 4 2 0 3 4 4 5 4 9 4 7 3 3 4 5 2 0 3 2 6 4 2 2 0 3 1 19 1 2 20 5 4 3 0 2 8 6 1 3 3 5 2 2 23 sink

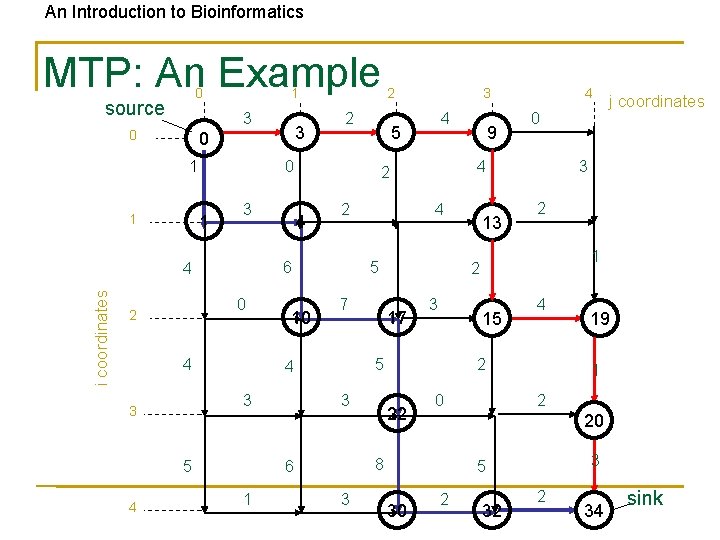
An Introduction to Bioinformatics MTP: An Example 0 source 1 3 0 1 1 1 3 i coordinates 4 4 10 5 4 7 17 3 0 13 3 2 1 15 4 2 22 0 19 1 2 20 8 3 5 30 j coordinates 3 2 5 3 9 4 4 5 6 1 4 5 2 4 3 3 3 2 6 0 2 2 0 4 4 3 0 2 2 34 sink

An Introduction to Bioinformatics MTP: Simple Recursive Program MT(n, m) x MT(n-1, m)+ length of the edge from (n- 1, m) to (n, m) y MT(n, m-1)+ length of the edge from (n, m-1) to (n, m) return max{x, y}

An Introduction to Bioinformatics MTP: Simple Recursive Program MT(n, m) x MT(n-1, m)+ length of the edge from (n- 1, m) to (n, m) y MT(n, m-1)+ length of the edge from (n, m-1) to (n, m) return max{x, y} Slow, for the same reason that Recursive. Change was slow

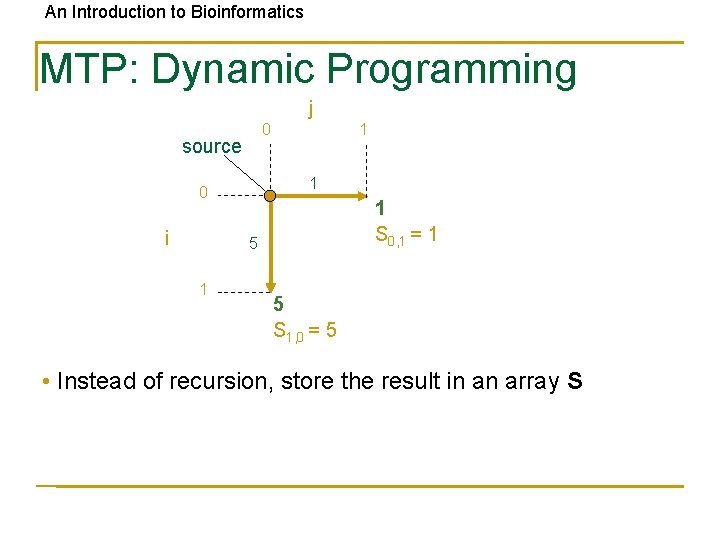
An Introduction to Bioinformatics MTP: Dynamic Programming j 0 source 1 0 i 1 1 S 0, 1 = 1 5 S 1, 0 = 5 • Instead of recursion, store the result in an array S

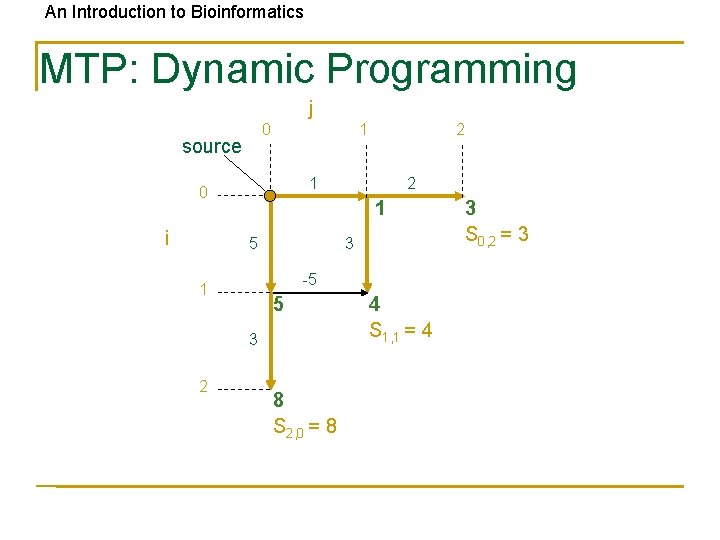
An Introduction to Bioinformatics MTP: Dynamic Programming j 0 source 1 1 0 i 2 1 5 3 -5 1 5 3 2 2 8 S 2, 0 = 8 4 S 1, 1 = 4 3 S 0, 2 = 3

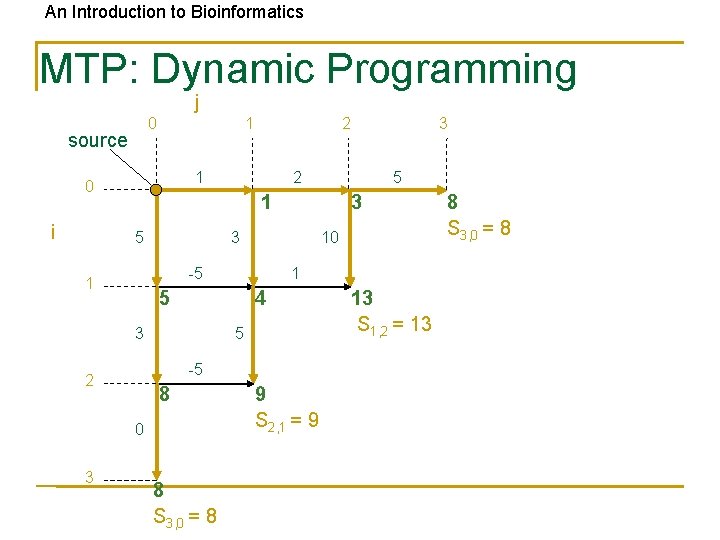
An Introduction to Bioinformatics MTP: Dynamic Programming j 0 source 1 1 0 i 5 3 3 10 -5 1 1 5 4 5 3 -5 2 8 0 8 S 3, 0 = 8 3 2 1 5 3 2 9 S 2, 1 = 9 13 S 1, 2 = 13 8 S 3, 0 = 8

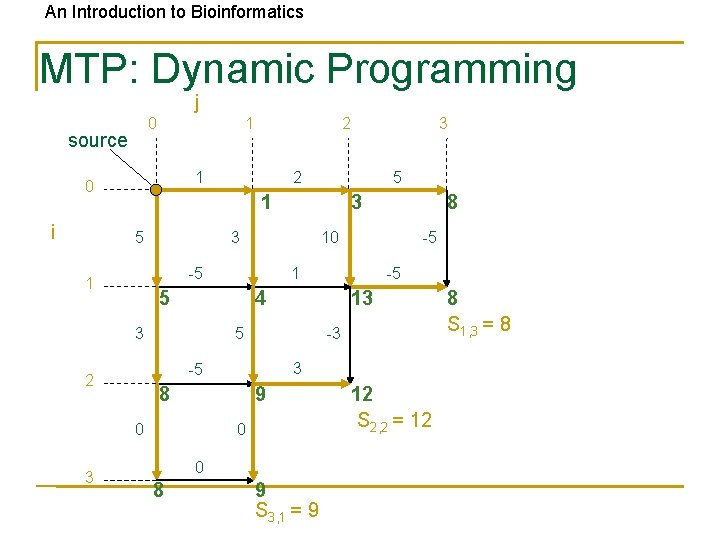
An Introduction to Bioinformatics MTP: Dynamic Programming j 0 source 1 1 0 i 5 13 5 -3 3 -5 8 9 0 0 0 8 -5 -5 4 3 8 10 1 5 2 3 3 -5 1 3 2 1 5 3 2 9 S 3, 1 = 9 12 S 2, 2 = 12 8 S 1, 3 = 8

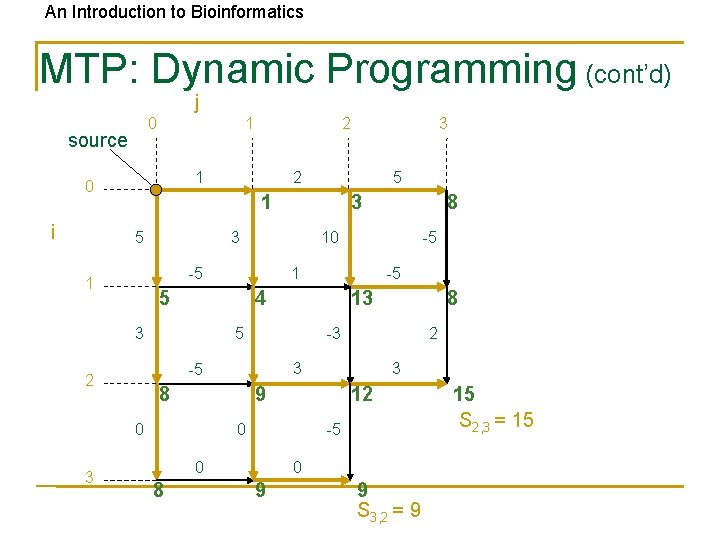
An Introduction to Bioinformatics MTP: Dynamic Programming (cont’d) j 0 source 1 1 0 i 5 13 5 3 9 12 0 -5 0 8 2 3 8 8 -3 -5 0 -5 -5 4 3 8 10 1 5 2 3 3 -5 1 3 2 1 5 3 2 0 9 9 S 3, 2 = 9 15 S 2, 3 = 15

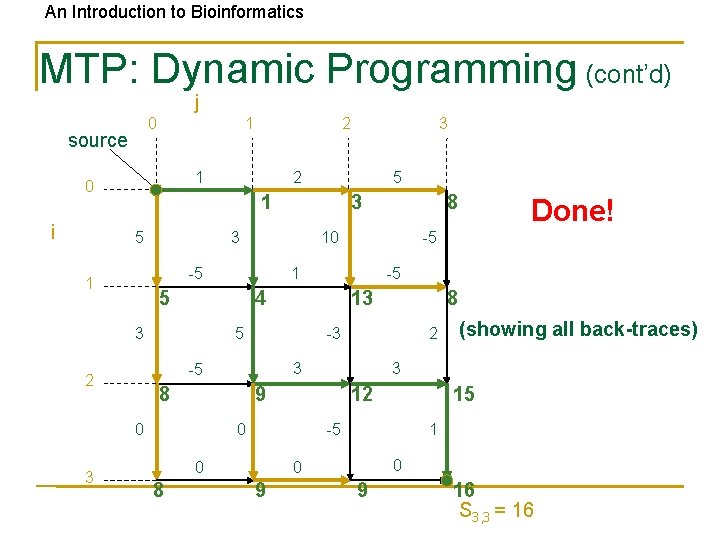
An Introduction to Bioinformatics MTP: Dynamic Programming (cont’d) j 0 source 1 1 0 i 5 12 15 -5 0 1 0 0 9 (showing all back-traces) 3 9 0 8 2 3 8 8 -3 -5 0 -5 13 5 Done! -5 4 3 8 10 1 5 2 3 3 -5 1 3 2 1 5 3 2 9 16 S 3, 3 = 16

An Introduction to Bioinformatics MTP: Recurrence Computing the score for a point (i, j) by the recurrence relation: si, j = max si-1, j + weight of the edge between (i-1, j) and (i, j) si, j-1 + weight of the edge between (i, j-1) and (i, j) the running time is n x m for a n by m grid (n = # of rows, m = # of columns)

An Introduction to Bioinformatics Manhattan is not a perfect grid 26

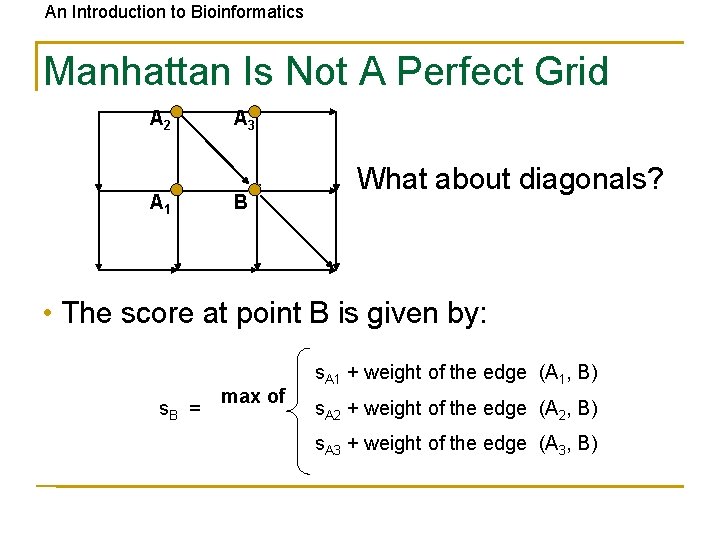
An Introduction to Bioinformatics Manhattan Is Not A Perfect Grid A 2 A 1 A 3 B What about diagonals? • The score at point B is given by: s. B = max of s. A 1 + weight of the edge (A 1, B) s. A 2 + weight of the edge (A 2, B) s. A 3 + weight of the edge (A 3, B)

An Introduction to Bioinformatics Manhattan Is Not A Perfect Grid (cont’d) Computing the score for point x is given by the recurrence relation: sx = max of sy + weight of vertex (y, x) where y є Predecessors(x) • Predecessors (x) – set of vertices that have • The running time for a graph G(V, E) vertices and E is the set of all edges) evaluated once edges leading to x (V is the set of all is O(E) since each edge is

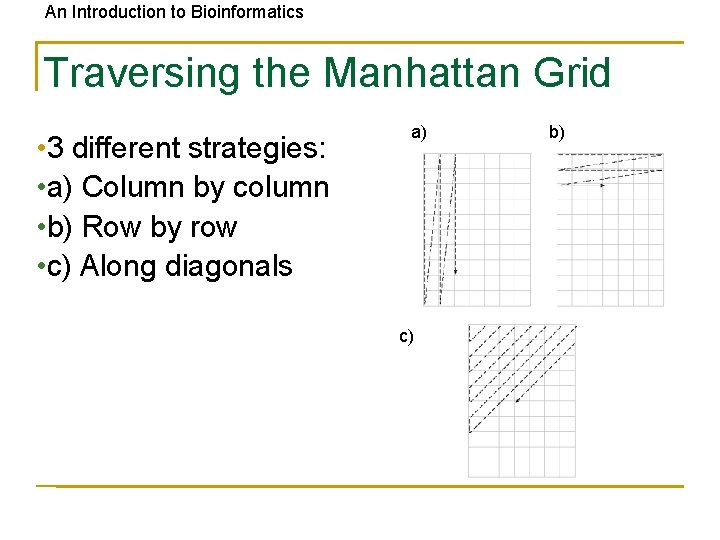
An Introduction to Bioinformatics Traversing the Manhattan Grid • 3 different strategies: • a) Column by column • b) Row by row • c) Along diagonals a) c) b)

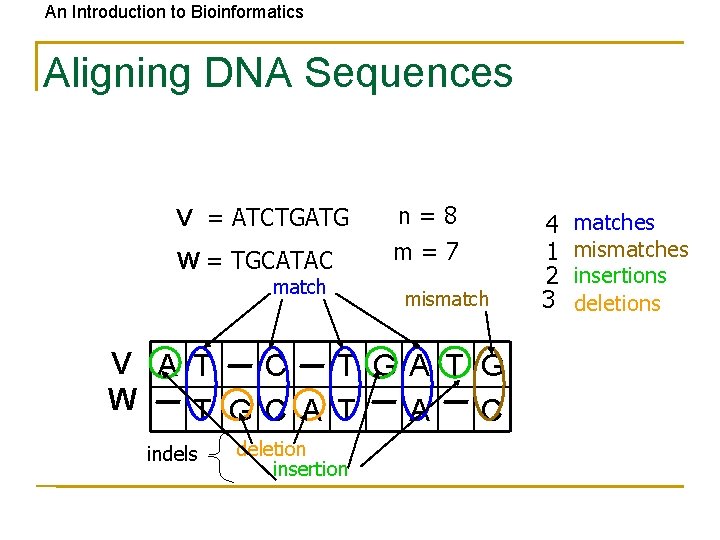
An Introduction to Bioinformatics Aligning DNA Sequences V = ATCTGATG W = TGCATAC match n=8 m=7 mismatch V A T C T GA T G W T GC A T A C indels deletion insertion 4 1 2 3 matches mismatches insertions deletions

An Introduction to Bioinformatics Longest Common Subsequence (LCS) Problem • Given two sequences v = v 1 v 2…vm and w = w 1 w 2…wn • The LCS of v and w is a sequence of positions in v: 1 < i 2 < … < it < m and a sequence of positions in w: 1 < j 2 < … < jt < n such that it -th letter of v equals to jt-letter of w and t is maximal

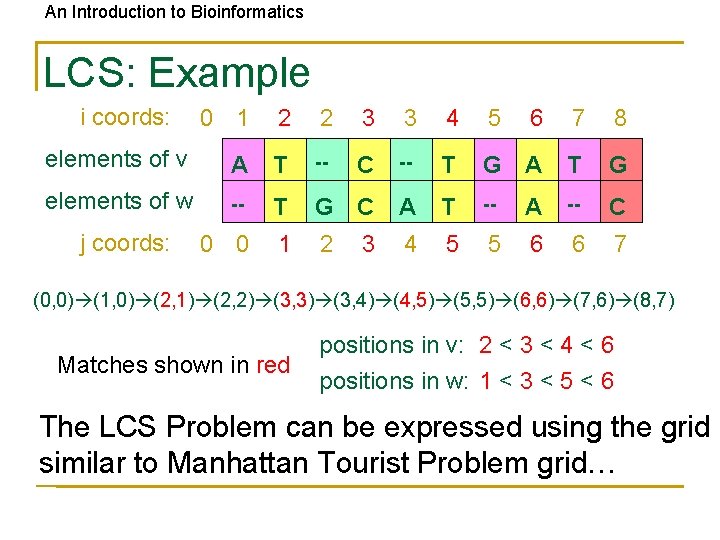
An Introduction to Bioinformatics LCS: Example i coords: 0 1 2 2 3 3 4 5 6 7 8 elements of v A T -- C -- T G A T G elements of w -- T G C A T -- A -- C 0 0 1 2 4 5 5 6 6 7 j coords: 3 (0, 0) (1, 0) (2, 1) (2, 2) (3, 3) (3, 4) (4, 5) (5, 5) (6, 6) (7, 6) (8, 7) Matches shown in red positions in v: 2 < 3 < 4 < 6 positions in w: 1 < 3 < 5 < 6 The LCS Problem can be expressed using the grid similar to Manhattan Tourist Problem grid…

An Introduction to Bioinformatics LCS: Dynamic Programming • Find the LCS of two strings Input: A weighted graph G with two distinct vertices, one labeled “source” one labeled “sink” Output: A longest path in G from “source” to “sink” • Solve using an LCS edit graph with diagonals replaced with +1 edges

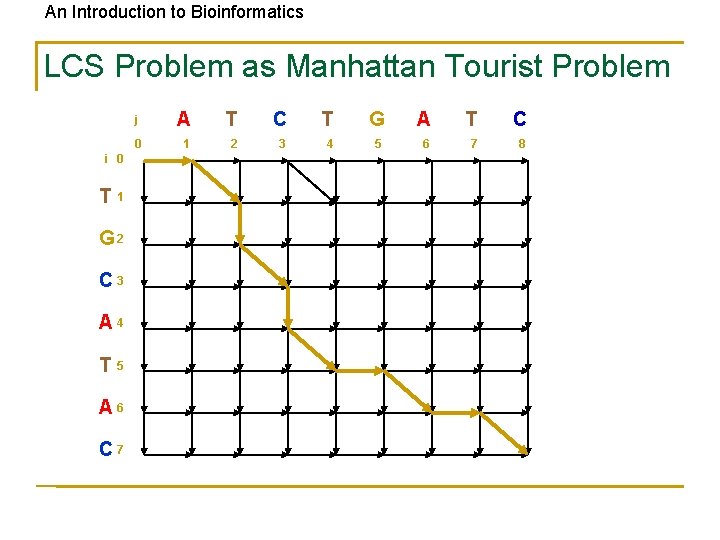
An Introduction to Bioinformatics LCS Problem as Manhattan Tourist Problem i 0 T 1 G 2 C 3 A 4 T 5 A 6 C 7 j A T C T G A T C 0 1 2 3 4 5 6 7 8

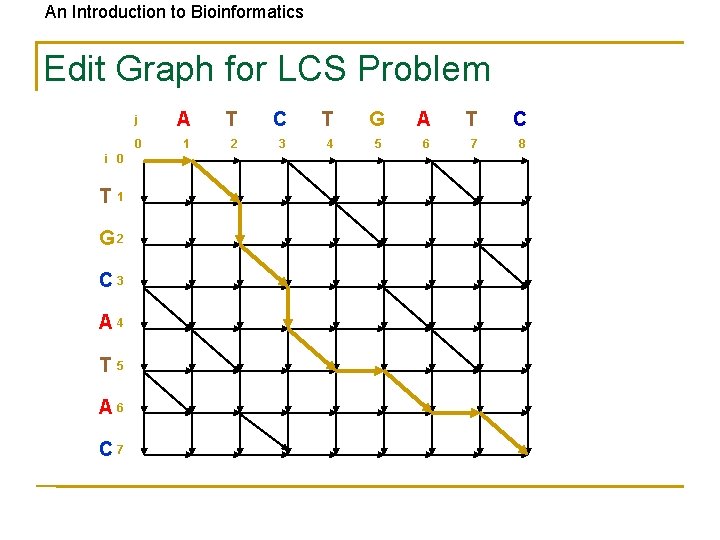
An Introduction to Bioinformatics Edit Graph for LCS Problem i 0 T 1 G 2 C 3 A 4 T 5 A 6 C 7 j A T C T G A T C 0 1 2 3 4 5 6 7 8

An Introduction to Bioinformatics Computing LCS Let vi = prefix of v of length i: v 1 … vi and wj = prefix of w of length j: w 1 … wj The length of LCS(vi, wj) is computed by: si, j = max si-1, j si, j-1 si-1, j-1 + 1 if vi = wj

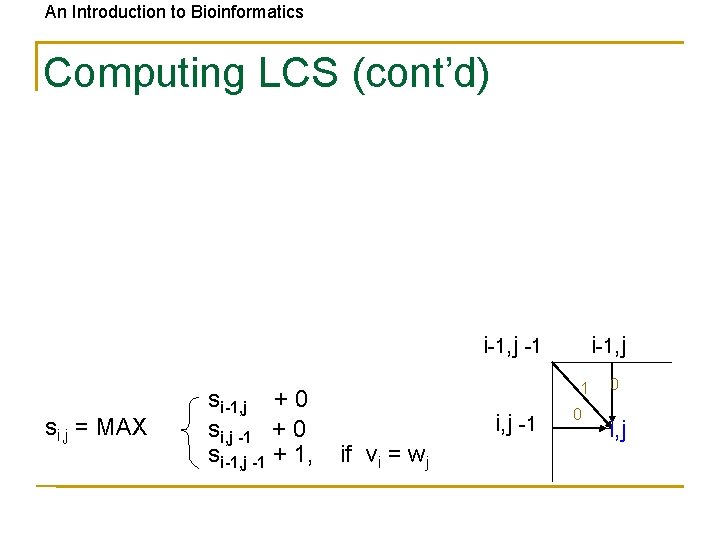
An Introduction to Bioinformatics Computing LCS (cont’d) i-1, j -1 si, j = MAX si-1, j + 0 si, j -1 + 0 si-1, j -1 + 1, 1 i, j -1 if vi = wj 0 0 i, j

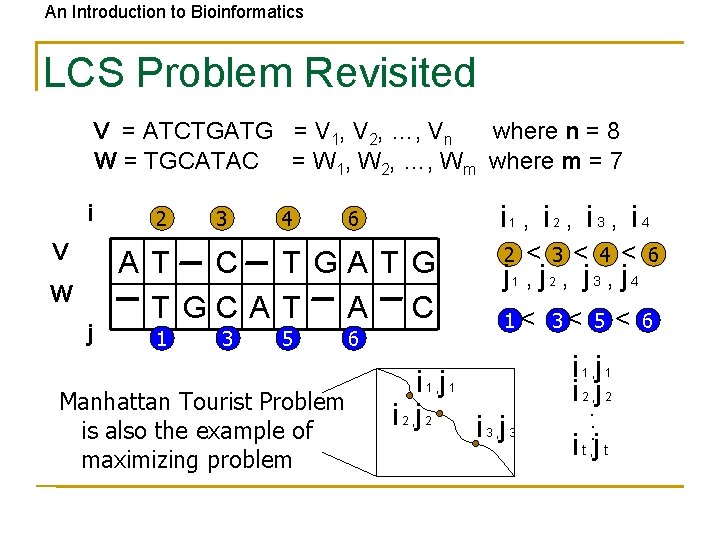
An Introduction to Bioinformatics LCS Problem Revisited V = ATCTGATG = V 1, V 2, …, Vn where n = 8 W = TGCATAC = W 1, W 2, …, Wm where m = 7 i V W j 2 3 4 i 6 AT C T GA T GCA T A C 1 3 5 Manhattan Tourist Problem is also the example of maximizing problem 6 , i 2 , i 3 , i 4 2 < 3 < 4 < 6 j 1 , j 2 , j 3 , j 4 1 1< 3< 5 i j i j 1, 1 2, 2 3, 3 i j 1, 1 2, 2 . . . it jt , < 6

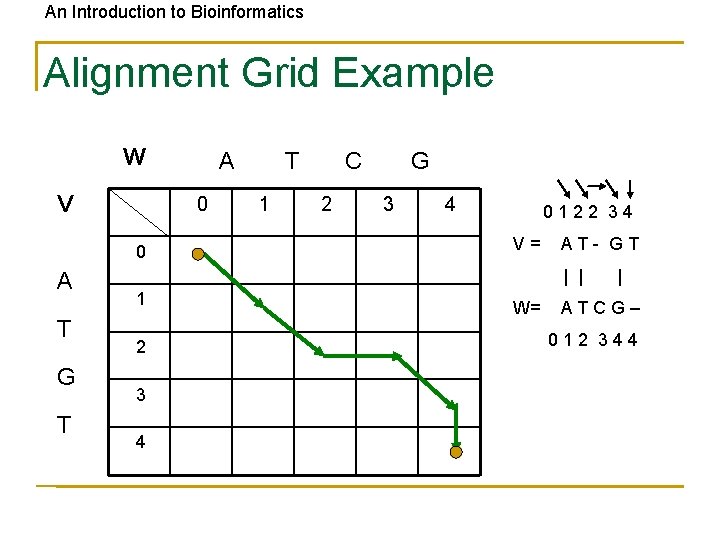
An Introduction to Bioinformatics Alignment Grid Example W V 0 0 A T G T A T 1 C 2 G 3 4 0122 34 V= AT- GT | | 1 2 3 4 W= | ATCG– 012 344

An Introduction to Bioinformatics Aligning Sequences without Insertions and Deletions: Hamming Distance Given two DNA sequences V and W : V : AT AT W : T AT A • The Hamming distance: d. H(V, W) = 8 is large but the sequences are very similar

An Introduction to Bioinformatics Aligning Sequences with Insertions and Deletions However, by shifting one sequence over one position: V : AT AT -W : -- T AT A • The edit distance: d. H(v, w) = 2. • Using Hamming distance neglects insertions and deletions in DNA

An Introduction to Bioinformatics Edit Distance Levenshtein (1966) introduced edit distance of two strings as the minimum number of elementary operations (insertions, deletions, and substitutions) to transform one string into the other d(v, w) = MIN no. of elementary operations to transform v w

An Introduction to Bioinformatics Edit Distance (cont’d) ith letter of v compare with letter of w V = ATAT W = TATA Just one shift Make it all line up V = - ATAT W = TATA Edit distance: d(v, w) = 2 (one insertion and one deletion)

An Introduction to Bioinformatics Edit Distance: Example • 5 edit operations: TGCATAT ATCCGAT • • • TGCATAT TGCATA TGCAT ATCCAT ATCCGAT (delete last T) (delete last A) (insert A at front) (substitute C for 3 rd G) (insert G before last A) (Done)

An Introduction to Bioinformatics Edit Distance: Example (cont’d) 4 edit operations: TGCATAT ATCCGAT TGCATAT (insert A at front) ATGCATAT (delete 6 th T) ATGCATA (substitute G for 5 th A) ATGCGTA (substitute C for 3 rd G) ATCCGAT (Done)

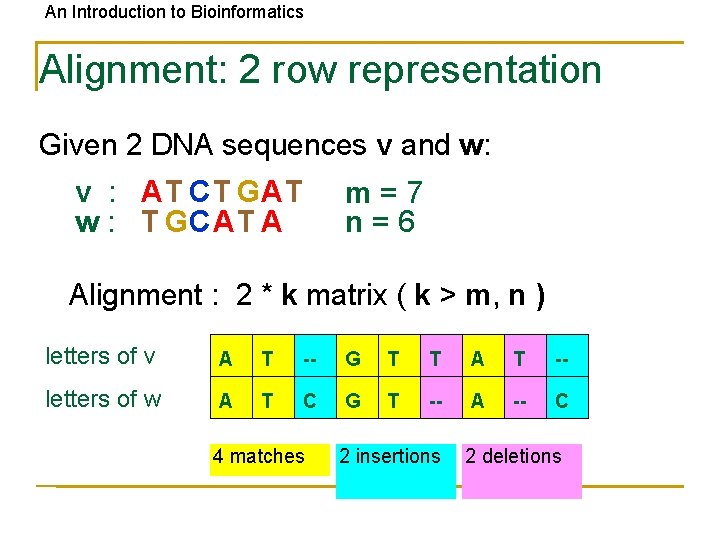
An Introduction to Bioinformatics Alignment: 2 row representation Given 2 DNA sequences v and w: v : AT CT GAT w : T GCAT A m=7 n=6 Alignment : 2 * k matrix ( k > m, n ) letters of v A T -- G T T A T -- letters of w A T C G T -- A -- C 4 matches 2 insertions 2 deletions

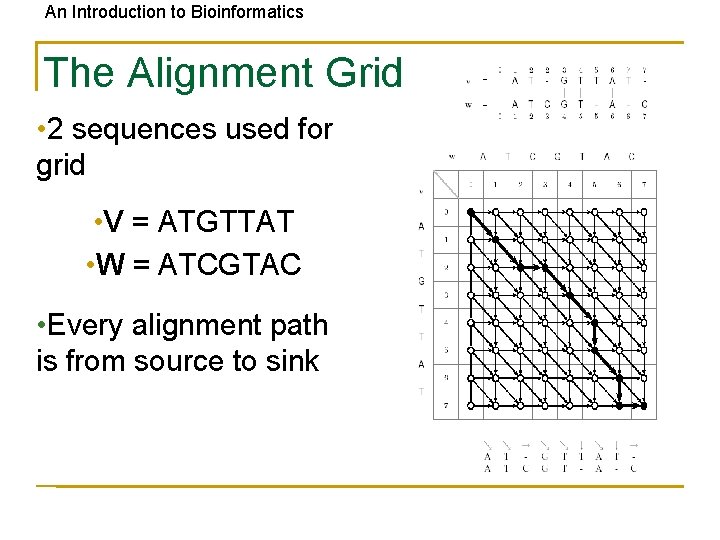
An Introduction to Bioinformatics The Alignment Grid • 2 sequences used for grid • V = ATGTTAT • W = ATCGTAC • Every alignment path is from source to sink

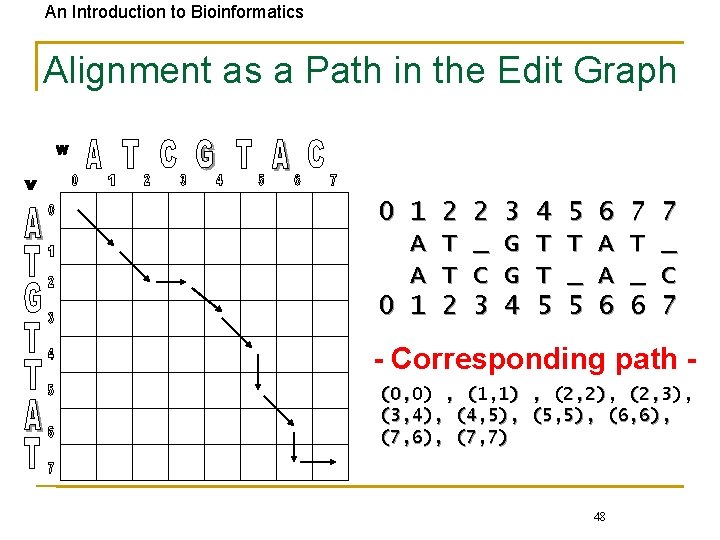
An Introduction to Bioinformatics Alignment as a Path in the Edit Graph 0 1 A A 0 1 2 T T 2 2 _ C 3 3 G G 4 4 T T 5 5 T _ 5 6 A A 6 7 T _ 6 7 _ C 7 - Corresponding path (0, 0) , (1, 1) , (2, 2), (2, 3), (3, 4), (4, 5), (5, 5), (6, 6), (7, 7) 48

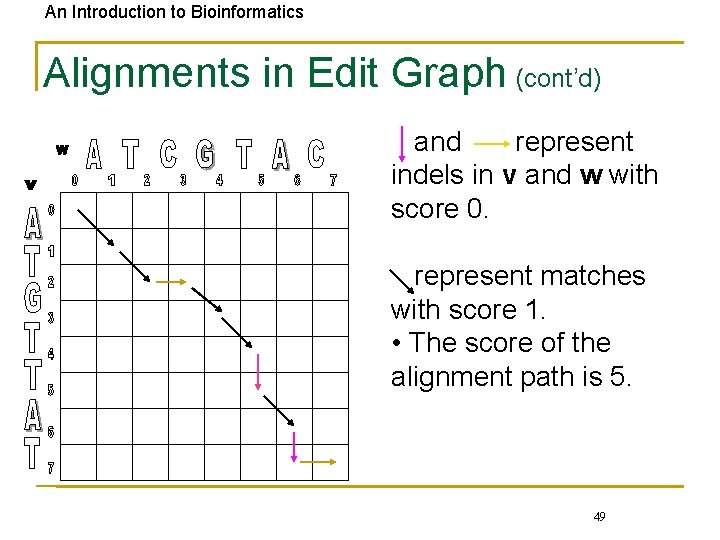
An Introduction to Bioinformatics Alignments in Edit Graph (cont’d) and represent indels in v and w with score 0. represent matches with score 1. • The score of the alignment path is 5. 49

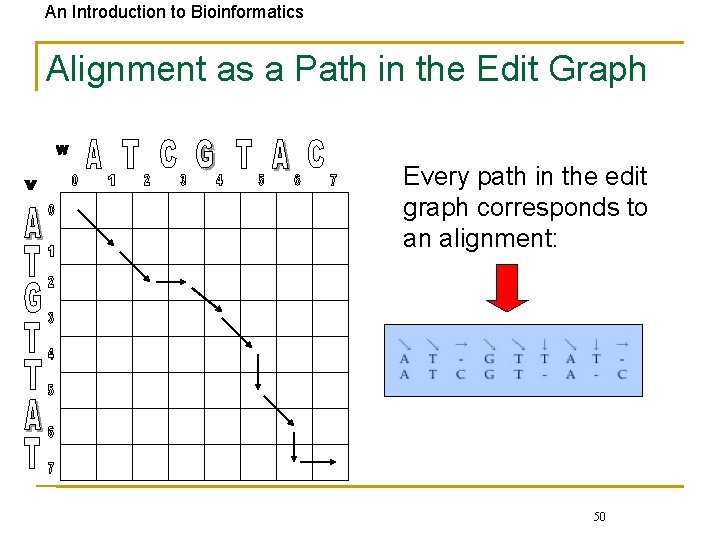
An Introduction to Bioinformatics Alignment as a Path in the Edit Graph Every path in the edit graph corresponds to an alignment: 50

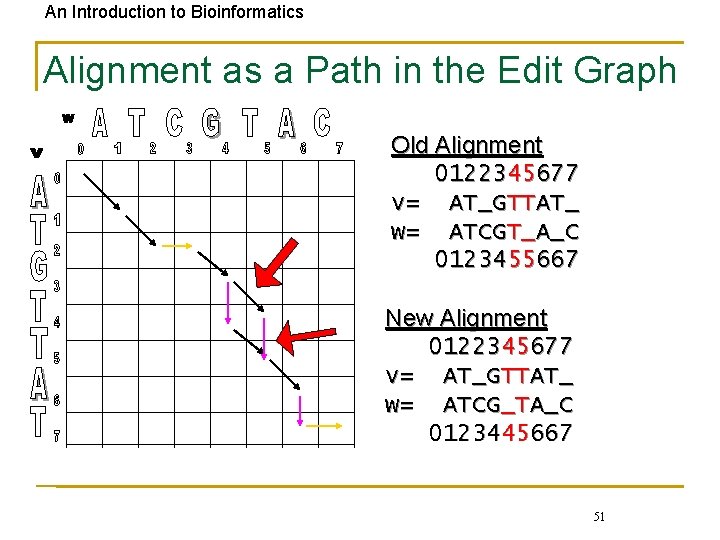
An Introduction to Bioinformatics Alignment as a Path in the Edit Graph Old Alignment 0122345677 v= AT_GTTAT_ w= ATCGT_A_C 0123455667 New Alignment 0122345677 v= AT_GTTAT_ w= ATCG_TA_C 0123445667 51

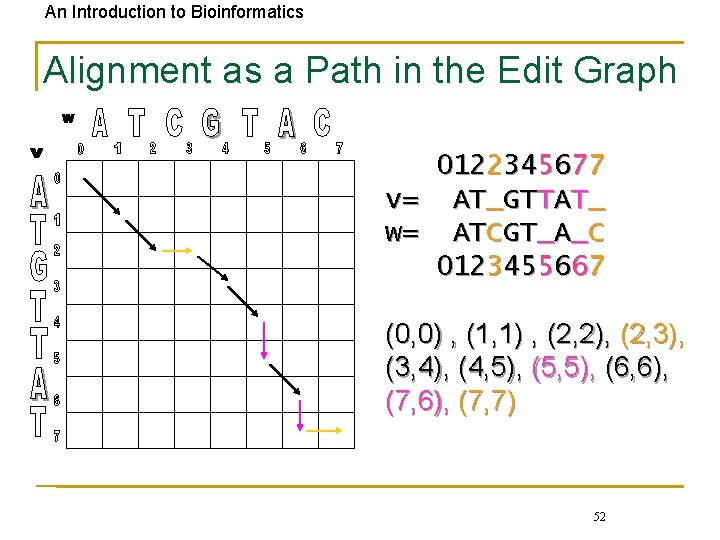
An Introduction to Bioinformatics Alignment as a Path in the Edit Graph 0122345677 v= AT_GTTAT_ w= ATCGT_A_C 0123455667 (0, 0) , (1, 1) , (2, 2), (2, 3), (3, 4), (4, 5), (5, 5), (6, 6), (7, 7) 52

An Introduction to Bioinformatics Alignment: Dynamic Programming si, j = max si-1, j-1+1 if vi = wj si-1, j si, j-1 53

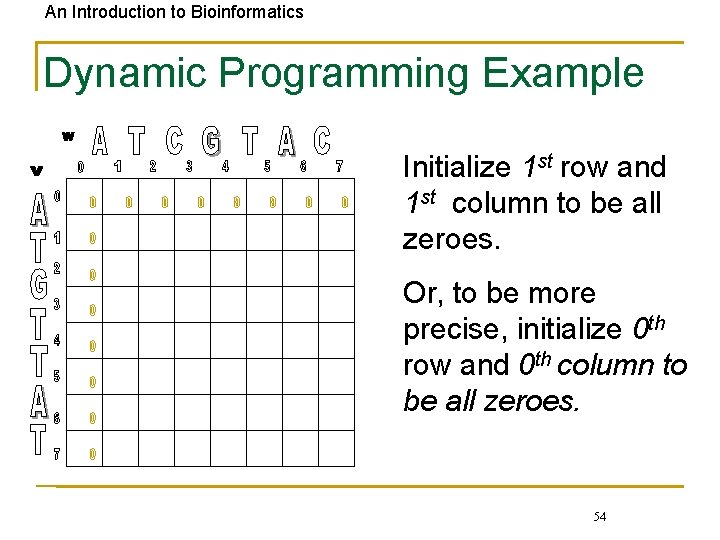
An Introduction to Bioinformatics Dynamic Programming Example Initialize 1 st row and 1 st column to be all zeroes. Or, to be more precise, initialize 0 th row and 0 th column to be all zeroes. 54

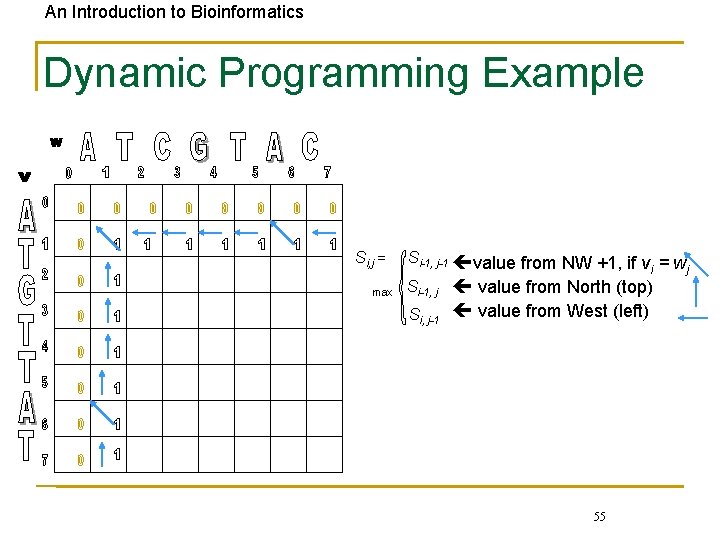
An Introduction to Bioinformatics Dynamic Programming Example Si, j = max Si-1, j-1 value from NW +1, if v = w i j Si-1, j value from North (top) Si, j-1 value from West (left) 55

An Introduction to Bioinformatics Alignment: Backtracking Arrows show where the score originated from. if from the top if from the left if vi = wj 56

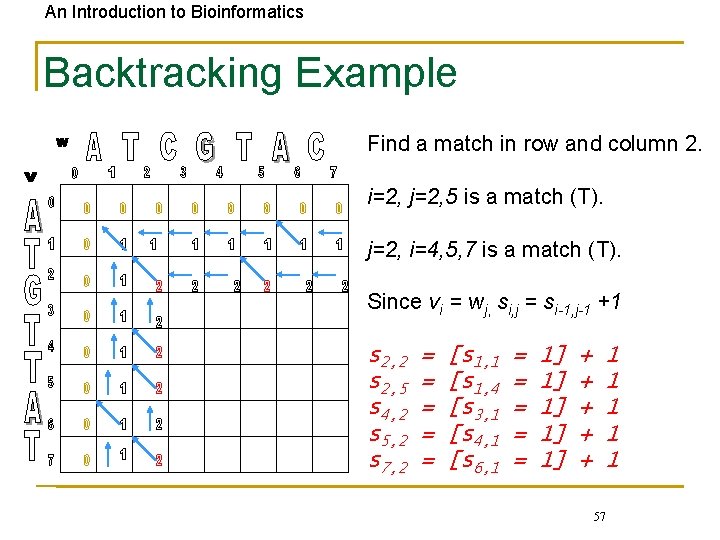
An Introduction to Bioinformatics Backtracking Example Find a match in row and column 2. i=2, j=2, 5 is a match (T). j=2, i=4, 5, 7 is a match (T). Since vi = wj, si, j = si-1, j-1 +1 s 2, 2 s 2, 5 s 4, 2 s 5, 2 s 7, 2 = = = [s 1, 1 [s 1, 4 [s 3, 1 [s 4, 1 [s 6, 1 = = = 1] 1] 1] + + + 1 1 1 57

An Introduction to Bioinformatics Backtracking Example Continuing with the dynamic programming algorithm gives this result. 58

An Introduction to Bioinformatics Alignment: Dynamic Programming si, j = max si-1, j-1+1 if vi = wj si-1, j si, j-1 59

An Introduction to Bioinformatics Alignment: Dynamic Programming si, j = max si-1, j-1+1 if vi = wj si-1, j+0 si, j-1+0 This recurrence corresponds to the Manhattan Tourist problem (three incoming edges into a vertex) with all horizontal and vertical edges weighted by zero. 60

An Introduction to Bioinformatics LCS Algorithm 1. LCS(v, w) 2. for i 1 to n 3. si, 0 0 4. for j 1 to m 5. s 0, j 0 6. for i 1 to n 7. for j 1 to m 8. si-1, j 9. si, j max si, j-1 10. si-1, j-1 + 1, if vi = wj 11. “ “ if si, j = si-1, j bi, j “ “ if si, j = si, j-1 • “ “ if si, j = si-1, j-1 + 1 • • return (sn, m, b) 61

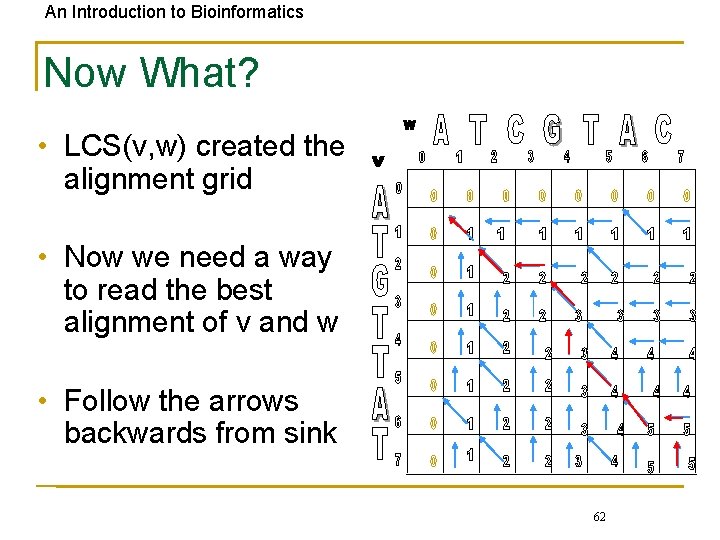
An Introduction to Bioinformatics Now What? • LCS(v, w) created the alignment grid • Now we need a way to read the best alignment of v and w • Follow the arrows backwards from sink 62

An Introduction to Bioinformatics Printing LCS: Backtracking 1. Print. LCS(b, v, i, j) 2. if i = 0 or j = 0 3. return 4. if bi, j = “ “ 5. Print. LCS(b, v, i-1, j-1) 6. print vi else 7. 8. if bi, j = “ “ 9. Print. LCS(b, v, i-1, j) 10. else 11. Print. LCS(b, v, i, j-1) 63

An Introduction to Bioinformatics LCS Runtime • It takes O(nm) time to fill in the nxm dynamic programming matrix. • Why O(nm)? The pseudocode consists of a nested “for” loop inside of another “for” loop to set up a nxm matrix. 64