An Introduction to Artificial Life Lecture 4 b

An Introduction to Artificial Life Lecture 4 b: Informed Search and Exploration Ramin Halavati (halavati@ce. sharif. edu) In which we see how information about the state space can prevent algorithms from blundering about the dark.

Local search algorithms • Some times the path to goal matters… – – Shortest route to a city. The solution to 8 -Puzzle. Robot’s route in a building. A Check-Mate • And some times, not – – 8 Queens. Job-Shop Scheduling Automatic program generation Check-Mate in Barareh!

Local search algorithms • When path doesn’t matter… • State space = set of "complete" configurations • Find configuration satisfying constraints • Keep a single "current" state or a fixed number of independent current states, try to improve it or them.

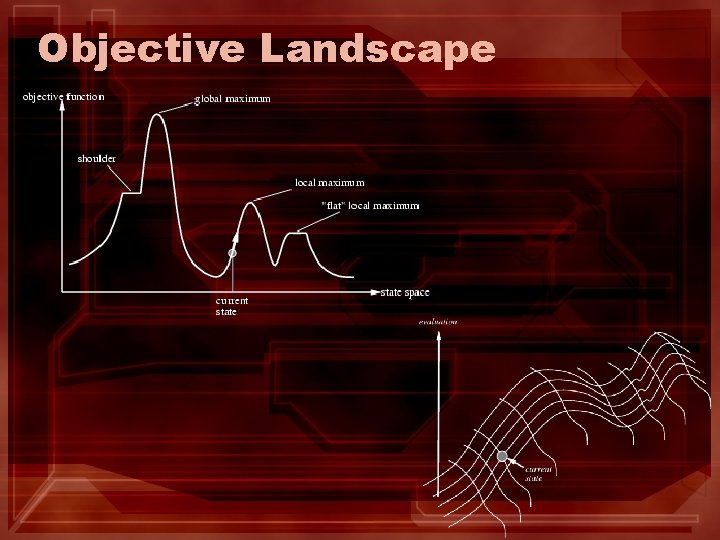
Objective Landscape

Hill-Climbing Search • "Like climbing Everest in thick fog with amnesia" • Greedy Local Search

Hill-Climbing Search: 8 -Queens • h = number of pairs of queens that are attacking each other, either directly or indirectly • h = 17 for the above state

Hill Climbing Problems • Local Maxima/Minima

Hill Climbing Problems • A local minimum with h = 1

Hill Climbing Problems • Ridges

Hill Climbing Problems • Plateaux – A state whose all neighbors have similar fitness.

Hill Climbing, Now What? • 8 -Queens, random examples: – 86% Failure, 14% Success. – In average, 4 moves. 8 – State Space: 8 > 17, 000 • Solution 1: Random Restart: – Restart from a random point if failed. • Almost 7 tries for 8 -queens. • 3, 000 queens in less than 1 minute.

Hill Climbing, Now What? • Solution 2: – Sideway moves for plateaux. / Limited. • Solution 3: – Stochastic Hill Climbing, random selection among up hills. • Slower convergence, sometimes better solutions. • Solution 4: – First Choice Hill Climbing.

Practical State Spaces

Simulated Annealing Search • Hill Climbing: – Just move to a better state. – Efficient, but can stuck in local maxima • Random Walk: – Move to a random neighbor. – Complete, but extremely inefficient. • Idea: Escape local maxima by allowing some "bad" moves but gradually decrease their frequency.

Simulated Annealing Search

Simulated Annealing Search • One can prove: If T decreases slowly enough, then simulated annealing search will find a global optimum with probability approaching 1 • Widely used in VLSI layout, airline scheduling, etc.

Local Beam Search • Keep track of k states rather than just one • Start with k randomly generated states • At each iteration, all the successors of all k states are generated • If any one is a goal state, stop; else select the k best successors from the complete list and repeat.

Local Beam Search • Looks similar to Parallel Random Start Hill Climbers, but it’s not. • Stochastic Beam Search

Genetic Algorithms • Beagle Voyage • Animals adopt to environmental.

Genetic Algorithms • Natural Evolution: – Given these requirements: 1. A creature whose features affects his reproduction rate. 2. Offspring features are very much, but not exactly similar to the parent(s). 3. There is a competition on resources. – We will have • Gradual Progress – The Blind Watchmaker - Dawkins

Genetic algorithms • Start with k randomly generated states (population) • A successor state is generated by combining two parent states • Produce the next generation of states by selection, crossover, and mutation. • Evaluation function (fitness function). Higher values for better states.

Genetic algorithms • Cross Over: – To select some part of the solution (state) from one person and the rest from another. • Mutation: – To change a small part of one solution with a small probability.

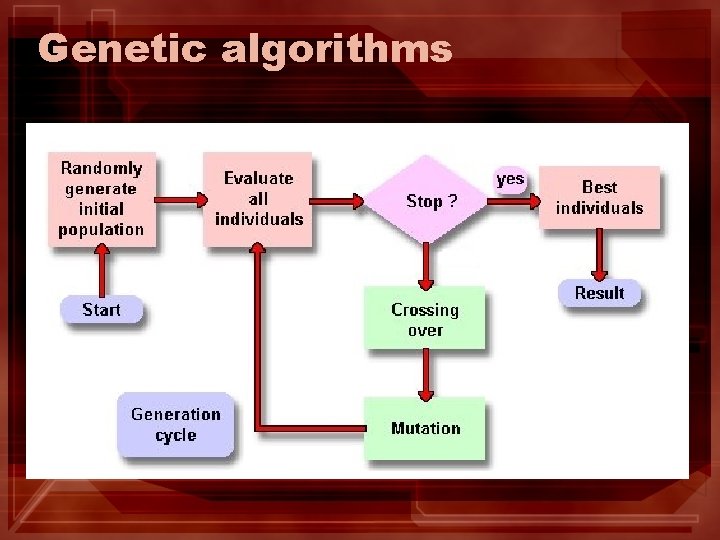
Genetic algorithms

L. S. in Continues Spaces • Infinite number of successor states. – To select three best locations for airports. • (x 1, y 1) , (x 2, y 2) , (x 3, y 3) • Approach 1: – To discretize • Just change them by ± • Approach 2: – To compute gradient! • J

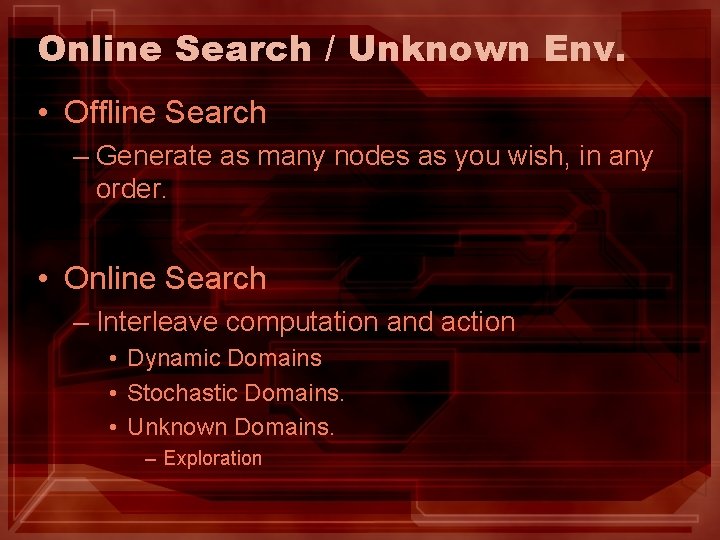
Online Search / Unknown Env. • Offline Search – Generate as many nodes as you wish, in any order. • Online Search – Interleave computation and action • Dynamic Domains • Stochastic Domains. • Unknown Domains. – Exploration

Online Search Problems • You can see the successors just by applying an action. • You may have different results from repeating a similar action at a certain state. • You just see one step ahead. G S

Algorithms for Online Search • • Nothing General Enough Limitation to Local Search Competitive Ratio Safely Explorable

Hill Climbing, once more… • Hill Climbing stores just one state, so it is an online searcher • But can not Randomly Restart. – Random Walk – Adding Memory: • Learning Real Time A*

Learning Real Time A* • To remember and update the costs of all visited nodes.

Learning Real Time A*

Essay Proposals • • What is MA*? Compare it with SMA* and A. * What is Tabu Search? What is Viterbi Search? What is Tree-Trellis? What are variants of Genetic Algorithms? What is Immunity System Search? What is Simulated DNA Computing Search? Compare Natural Evolution and Genetic Algorithms.

Essay Proposals • What is Game of Life? • What other search method exist that are inspired from nature?

Essay Proposals • Bring a survey of any of the proposed algorithms in real applications. • Bring a detailed usage of one of the algorithms in a real application. • Choose 5 exercises and do them in details, from any chapter, but tell me first.

Exercises • • Choose one of 4. 15 – 4. 18 Due: Esfand 30 th Email To: ghanbari@ce. sharif. edu Subject: AIEX-415. . AIEX-418

Project Proposals • Make an improvement in one of the algorithms, compare your results with original one on different domains. • …

Project Proposals • Choose a real problem. Design and implement a suitable algorithm for it. Compare your results with required results or other solutions.

Project Proposals • Choose a one player game, find some other people who agree on yours. Write a common engine and perform a competition, with or without time limit. – Mahjongg, Solitaire, Open Tetris, …

That’s all.