An Intoduction to Carbon Nanotubes By Shaun Ard

An Intoduction to Carbon Nanotubes By: Shaun Ard Physics 672

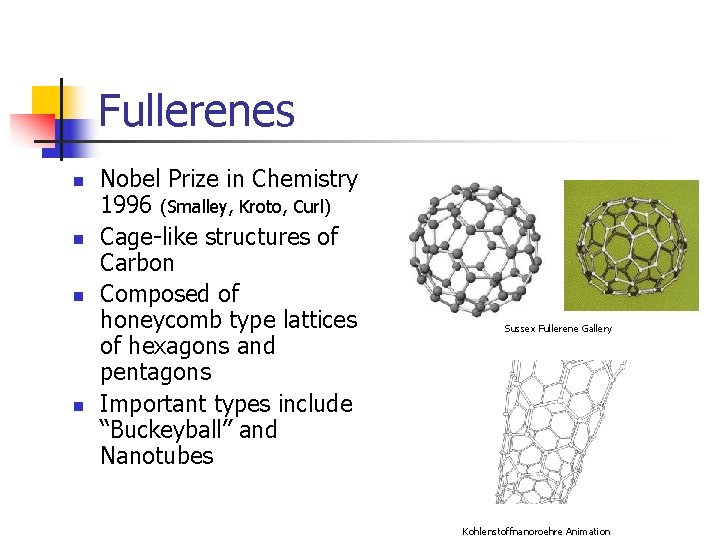
Fullerenes n n Nobel Prize in Chemistry 1996 (Smalley, Kroto, Curl) Cage-like structures of Carbon Composed of honeycomb type lattices of hexagons and pentagons Important types include “Buckeyball” and Nanotubes Sussex Fullerene Gallery Kohlenstoffnanoroehre Animation

Nanotube Discovery n n Carbon filaments had long been known, but nanotube discovery credited to S. Iijima in 1991 Discovered by chance during investigation of fullerene production Y. Ando et al, Growing Carbon Nanotubes, Materials Today, Oct (2004) 22

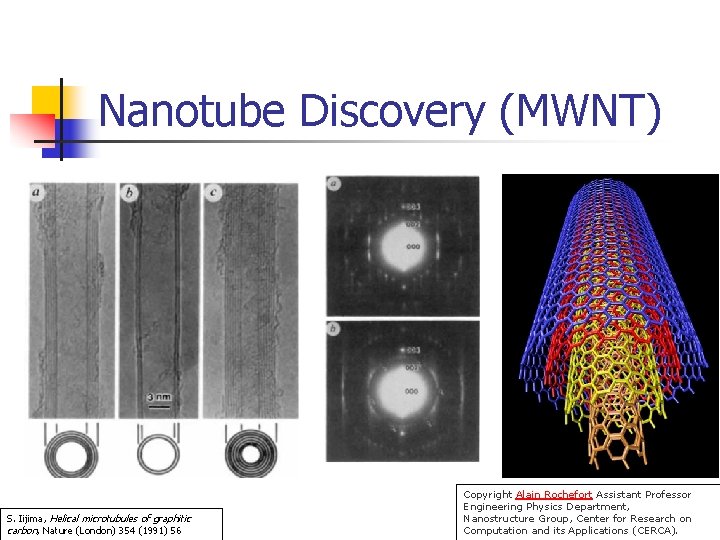
Nanotube Discovery (MWNT) S. Iijima, Helical microtubules of graphitic carbon, Nature (London) 354 (1991) 56 Copyright Alain Rochefort Assistant Professor Engineering Physics Department, Nanostructure Group, Center for Research on Computation and its Applications (CERCA).

Nanotube Discovery (SWNT) S. Iijima et al, Single-shell carbon nanotubes of 1 -nm diameter, Nature (London) 363 (1993) 603 D. S. Bethune et al, Cobalt-catalysed growth of carbon nanotubes with single-atomic-layer walls, Nature (London) 363 (1993) 605

Synthesis Enhancement n Laser-Furnace method n High quality SWNTs n Diameter control n New materials“peapods” n Allows for study of formation dynamics Reprinted from Mater. Today, 7, Y. Ando, X. Zhao, T. Sugai, and M. Kumar, “Growing Carbon Nanotubes, ” 22– 29, Copyright 2004, with permission from Elsevier.

Synthesis Enhancement cont. n Catalytic Chemical Vapor Deposition n Allows for growth of aligned nanotubes n Use of a variety of substrates or surfaces n Easily scaled up for increased production Firstnano “Easy. Tube 3000”

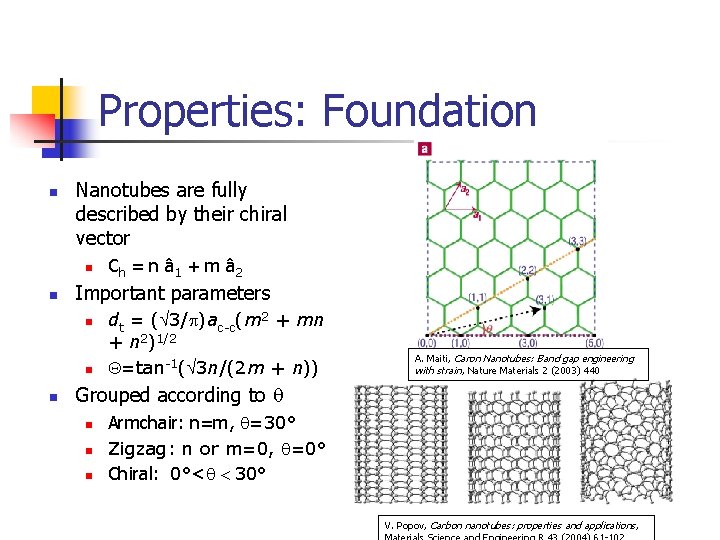
Properties: Foundation n Nanotubes are fully described by their chiral vector n n Important parameters n n n Ch = n â 1 + m â 2 dt = (Ö 3/p)ac-c(m 2 + mn + n 2)1/2 Q=tan-1(Ö 3 n/(2 m + n)) A. Maiti, Caron Nanotubes: Band gap engineering with strain, Nature Materials 2 (2003) 440 Grouped according to q n n n Armchair: n=m, q=30° Zigzag: n or m=0, q=0° Chiral: 0°<q < 30° V. Popov, Carbon nanotubes: properties and applications,

Properties: Electronic n n 1 -D band structure calculated from 2 -D graphene band structure using “zone folding” scheme Ekμ= E 2 D(k*K 2/|K 2|+μK 1) n K 1=(-t 2 b 1+ t 1 b 2)/ N n K 2=(mb 1 - nb 2)/ N (5, 5) (9, 0) (10, 0) V. Popov, Carbon nanotubes: properties and applications,

Properties: Electronic cont. n Theory predicts nanotubes exhibit both metallic and semi-conducting behavior n n |n-m| evenly divisible by 3 - metallic All others semiconducting with a band gap inversely proportional to the tube diameter T. W. Odomet al, Atomic Structure and Electronic Properties of Single-Walled Nanotubes, Nature (London) 391 (1998) 62

Properties: Mechanical n Young’s Modulus n n On the order of 1 Tpa (steel ~200 GPa) No dependence on diameter for MWNTs but strong dependence for SWNTs J. Salvetat, Elastic Modulus of Ordered and Disordered Multiwalled Carbon Nanotubes, Adv. Mater. 11 (1999) 161

Applications Nano-Wires

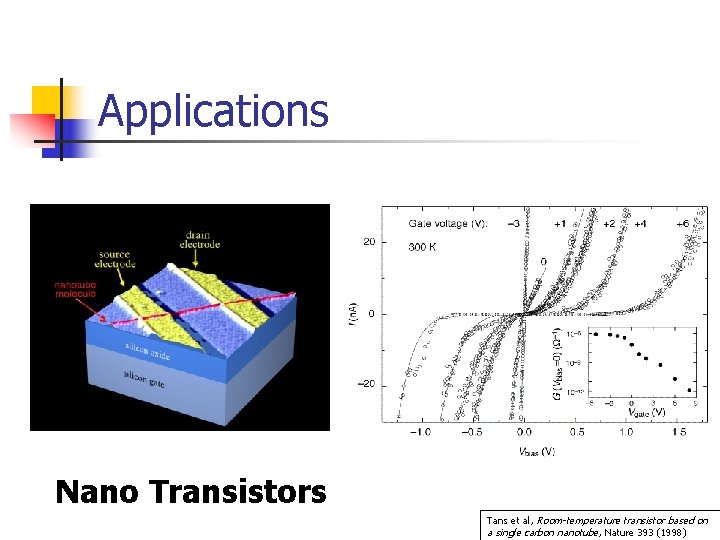
Applications Nano Transistors Tans et al, Room-temperature transistor based on a single carbon nanotube, Nature 393 (1998)

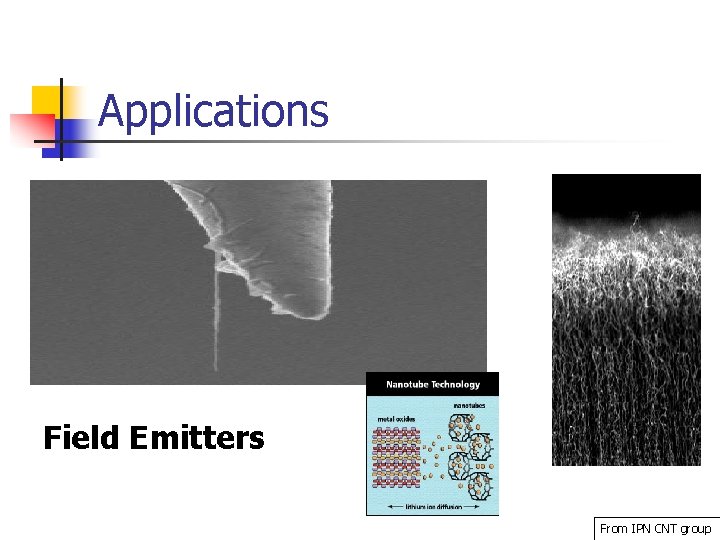
Applications Field Emitters From IPN CNT group

Applications J. Fischer, Matt Ray/EHP Lithium Ion Batteries MIT/Riccardo Signorelli Ultra Capacitors Charge Storage

Conclusion Nano =