An Improved Algorithm for Maintaining Arc Consistency in

An Improved Algorithm for Maintaining Arc Consistency in Dynamic Constraint Satisfaction Problems Roman Barták Charles University Prague Pavel Surynek Czech Technical University Prague roman. bartak@mff. cuni. cz pavel. surynek@seznam. cz

Problem area n Real world = dynamic world n practical problems change continuously n difficult to capture by static formulation n solution must reflect that changes n Dynamic CSP n A CSP from which constraints can be retracted or to which constraints can be added in arbitrary order.

Existing approaches to DCSPs n Search for robust solution n the solution is still valid for the problem after a small change n Reconstruction of the solution n the solution is locally repaired after a change n Minimal perturbation problems n solutions minimizing that local repair n Reusing the reasoning process n our approach: maintaining arc consistency

Why dynamic arc consistency ? n Arc consistency simplifies the problem n Interactive problems n Interactive preparation of consistent a problem n n n peptide synthesis determination of RNA structures timetabling n Search algorithms n Decision = addition of a constraint n Undoing decision = retraction of a constraint

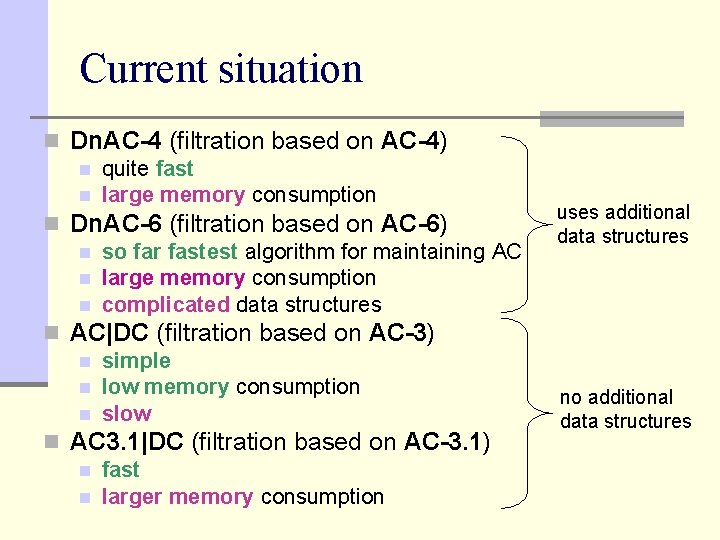
Current situation n Dn. AC-4 (filtration based on AC-4) n quite fast n large memory consumption n Dn. AC-6 (filtration based on AC-6) n so far fastest algorithm for maintaining AC n large memory consumption n complicated data structures n AC|DC (filtration based on AC-3) n simple n low memory consumption n slow n AC 3. 1|DC (filtration based on AC-3. 1) n fast n larger memory consumption uses additional data structures no additional data structures

3 phases of constraint retraction n Initialization phase restores n values deleted by the retracted constraint from domains of its variables when propagating through it for the first time n Propagation phase restores n values that can be added due to previous domain extensions (like reverted AC) n Filtration phase removes n inconsistent values (standard AC)

A new algorithm AC|DC-2 i n Record information during addition of constraints via AC-3 n justifications (like Dn. ACs, neighbor in which lost all supports) and value removal time n Restore only most promising values n use removal times and justifications to identify values to restore n n new support in justification variable that was deleted before restored value n Optionally use AC-3. 1 AC 3. 1|DC-2 i

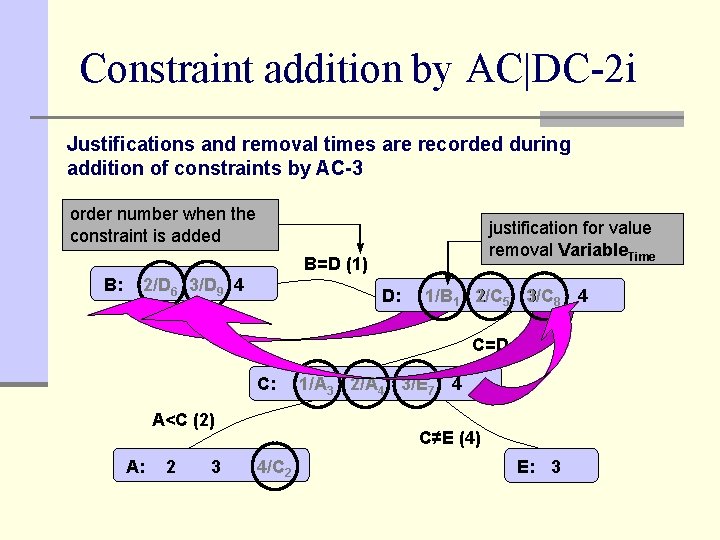
Constraint addition by AC|DC-2 i Justifications and removal times are recorded during addition of constraints by AC-3 order number when the constraint is added justification for value removal Variable. Time B=D (1) B: 2 6 3/D 2/D 3 9 4 D: 1 1 2/C 1/B 2 5 3/C 3 8 4 C=D (3) C: A<C (2) A: 2 3 1/A 1 3 2/A 2 4 3/E 3 7 4 C≠E (4) 4 2 4/C E: 3

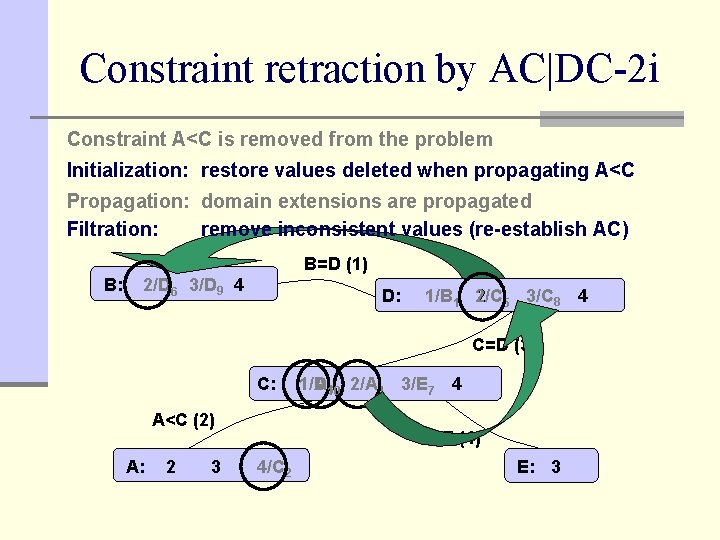
Constraint retraction by AC|DC-2 i Constraint A<C is removed from the problem Initialization: restore values deleted when propagating A<C Propagation: domain extensions are propagated Filtration: remove inconsistent values (re-establish AC) B=D (1) B: 2 6 3/D 9 4 2/D D: 2 5 3/C 8 4 1/B 1 2/C C=D (3) C: A<C (2) A: 2 3 1/A 1/D 1 10 2 4 3/E 7 4 3 2/A C≠E (4) 4/C 4 2 E: 3

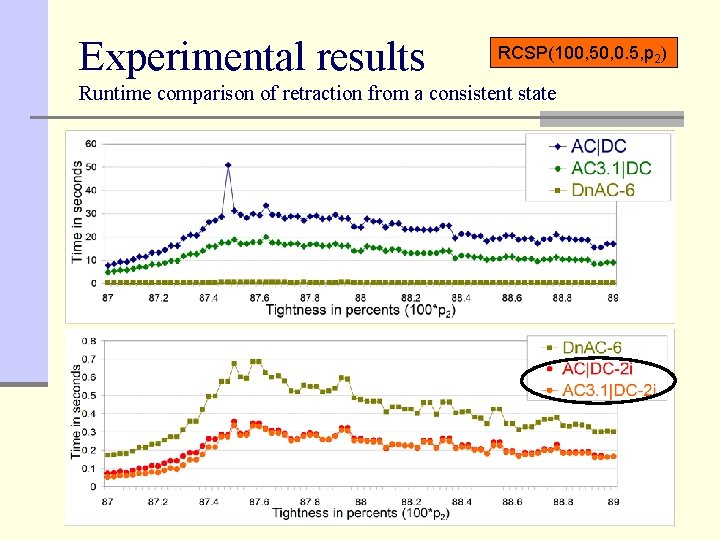
Experimental results RCSP(100, 50, 0. 5, p 2) Runtime comparison of retraction from a consistent state

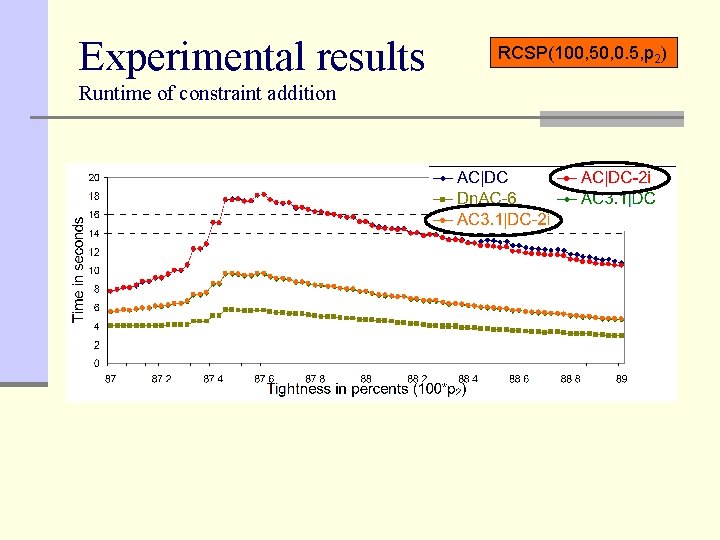
Experimental results Runtime of constraint addition RCSP(100, 50, 0. 5, p 2)

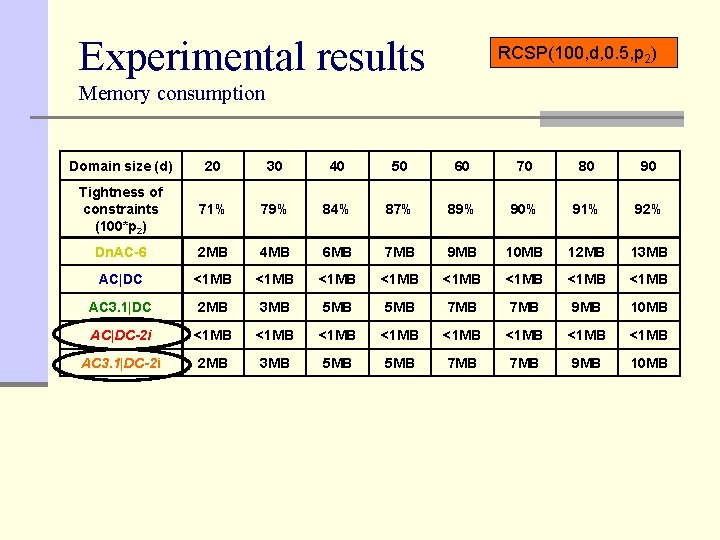
Experimental results RCSP(100, d, 0. 5, p 2) Memory consumption Domain size (d) 20 30 40 50 60 70 80 90 Tightness of constraints (100*p 2) 71% 79% 84% 87% 89% 90% 91% 92% Dn. AC-6 2 MB 4 MB 6 MB 7 MB 9 MB 10 MB 12 MB 13 MB AC|DC <1 MB <1 MB AC 3. 1|DC 2 MB 3 MB 5 MB 7 MB 9 MB 10 MB AC|DC-2 i <1 MB <1 MB AC 3. 1|DC-2 i 2 MB 3 MB 5 MB 7 MB 9 MB 10 MB

Conclusions n New algorithm for maintaining arc consistency AC|DC-2 i practical time of constraint retraction better than Dn. AC-6 (so far fastest) n low memory consumption (like simple AC|DC) n n Optionally use AC-3. 1 AC 3. 1|DC-2 i n improves time of constraint addition n larger memory consumption