An Image Filtering Technique for SPIDER Visible Tomography

An Image Filtering Technique for SPIDER Visible Tomography N. Fonnesu M. Agostini, M. Brombin, R. Pasqualotto, G. Serianni 3 rd Ph. D Event- York- 24 th-26 th June 2013

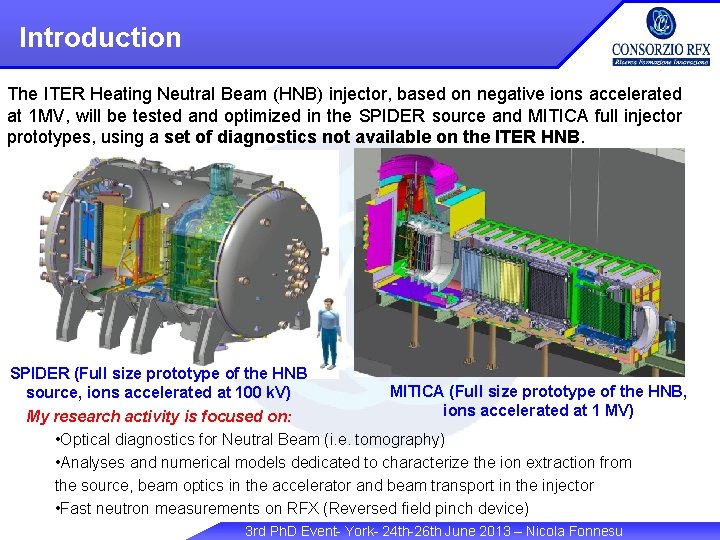
Introduction The ITER Heating Neutral Beam (HNB) injector, based on negative ions accelerated at 1 MV, will be tested and optimized in the SPIDER source and MITICA full injector prototypes, using a set of diagnostics not available on the ITER HNB. SPIDER (Full size prototype of the HNB source, ions accelerated at 100 k. V) MITICA (Full size prototype of the HNB, ions accelerated at 1 MV) My research activity is focused on: • Optical diagnostics for Neutral Beam (i. e. tomography) • Analyses and numerical models dedicated to characterize the ion extraction from the source, beam optics in the accelerator and beam transport in the injector • Fast neutron measurements on RFX (Reversed field pinch device) 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu

Outline • Tomography: • what is it? • why is it important in SPIDER ? • tomography code and inversion technique • The role of instrumental noise in tomography reconstructions • Filtering technique in the spatial domain and results • Conclusions and future works 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu

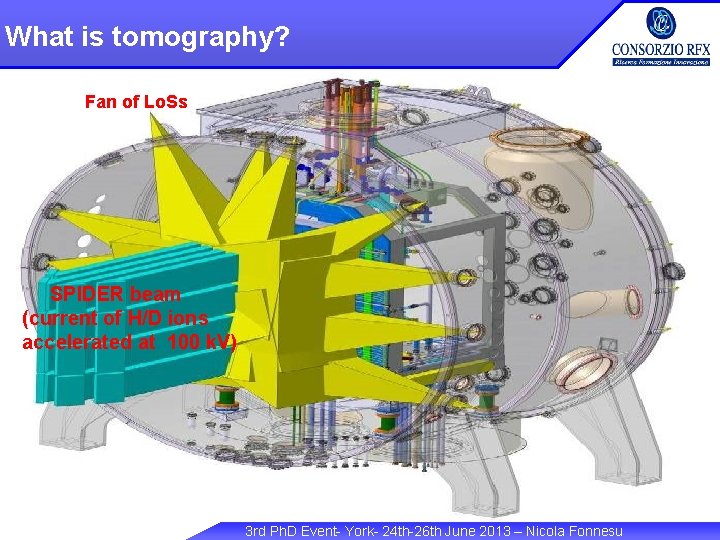
What is tomography? Tomography the reconstruction of a cross-section (or a slice) of an object Fan of is Lo. Ss from its projections (i. e. integral of the image at a given angle). Fan of. SPIDER Lo. Ss beam (current of H/D ions accelerated at 100 k. V) Every projection is made of a large number of lines of sight (Lo. Ss) 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu

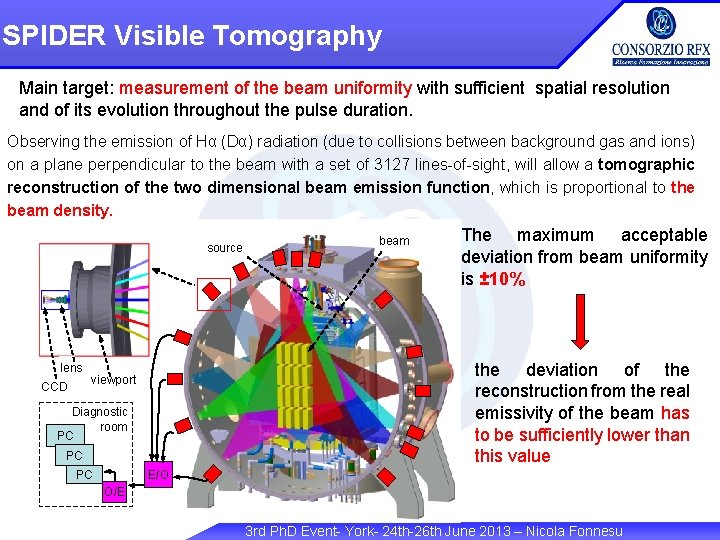
SPIDER Visible Tomography Main target: measurement of the beam uniformity with sufficient spatial resolution and of its evolution throughout the pulse duration. Observing the emission of Hα (Dα) radiation (due to collisions between background gas and ions) on a plane perpendicular to the beam with a set of 3127 lines-of-sight, will allow a tomographic reconstruction of the two dimensional beam emission function, which is proportional to the beam density. source lens CCD The maximum acceptable deviation from beam uniformity is ± 10% the deviation of the reconstruction from the real emissivity of the beam has to be sufficiently lower than this value viewport Diagnostic room PC PC PC beam E/O O/E 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu

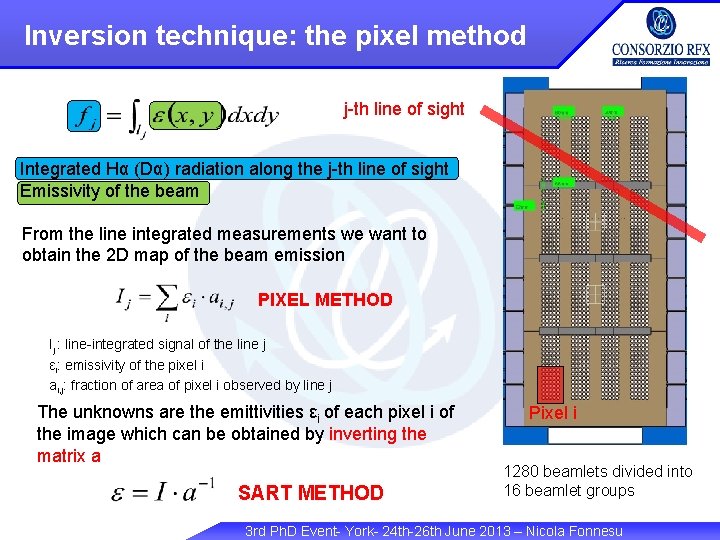
Inversion technique: the pixel method j-th line of sight Integrated Hα (Dα) radiation along the j-th line of sight Emissivity of the beam From the line integrated measurements we want to obtain the 2 D map of the beam emission PIXEL METHOD Ij : line-integrated signal of the line j εi: emissivity of the pixel i ai, j: fraction of area of pixel i observed by line j The unknowns are the emittivities εi of each pixel i of the image which can be obtained by inverting the matrix a SART METHOD Pixel i 1280 beamlets divided into 16 beamlet groups 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu

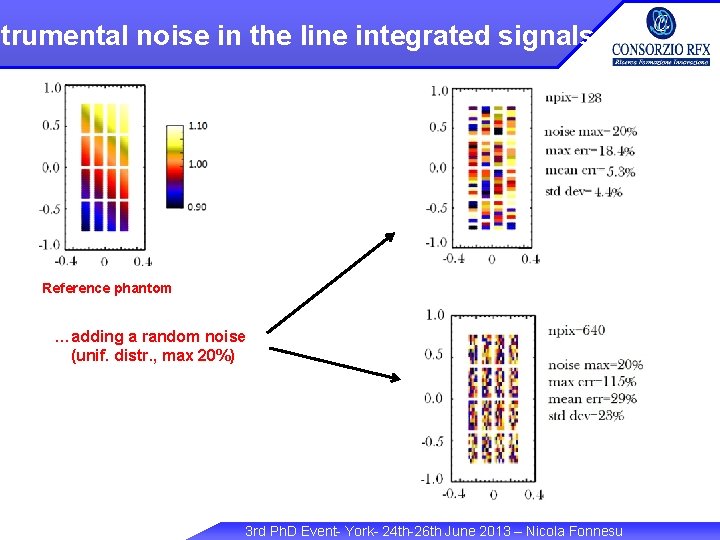
strumental noise in the line integrated signals Phantoms (i. e. 2 D emissivity profiles) that reproduce different experimental beam configurations (non-uniformity of ± 10%, uniform profile, two beamlet groups turned off) are simulated and reconstructed by the tomography code with satisfactory results. ± 10% Reference phantom …adding a random noise (unif. distr. , max 20%) However, if we simulate noisy input data, errors in the reconstructed image shows that noise acts as a limiting factor for the maximum achievable resolution. 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu

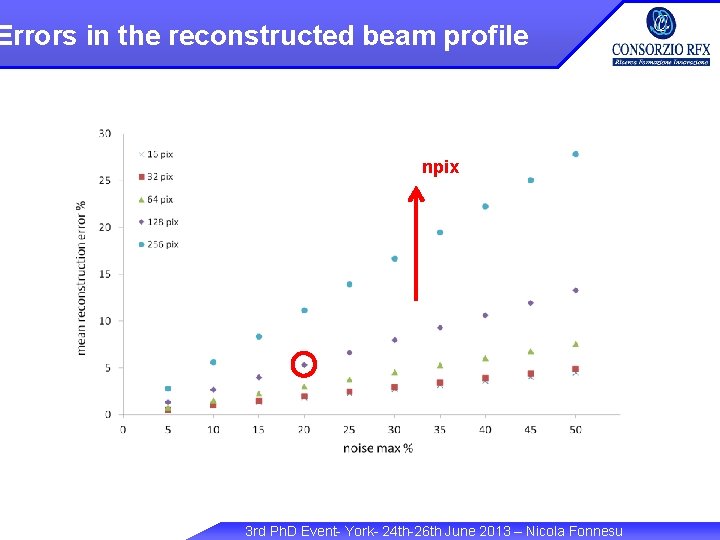
Errors in the reconstructed beam profile npix 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu

Filtering in the spatial domain The filtering algorithm is based on Lee’s formula [1] that allows to calculate the estimated noise-free pixel intensity just considering its neighborhood: this value will represent the filtered intensity for the corresponding pixel. Pixel’s neighborhood is defined by a squared window (5 x 5 pixels gives better results) Pixel i, j filtered value of the pixel i, j at the step l+1 value of the pixel i, j at the step l parameter (variance, mean of the pixel’s neighborhood) local average pixel’s value at the step l [1] J. S. Lee, Optical Engineering 25 (5), 636 -646 (1986) 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu

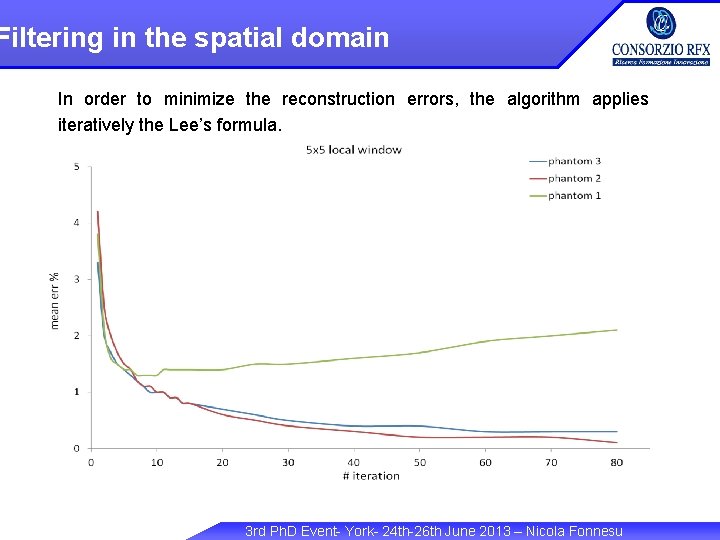
Filtering in the spatial domain In order to minimize the reconstruction errors, the algorithm applies iteratively the Lee’s formula. 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu

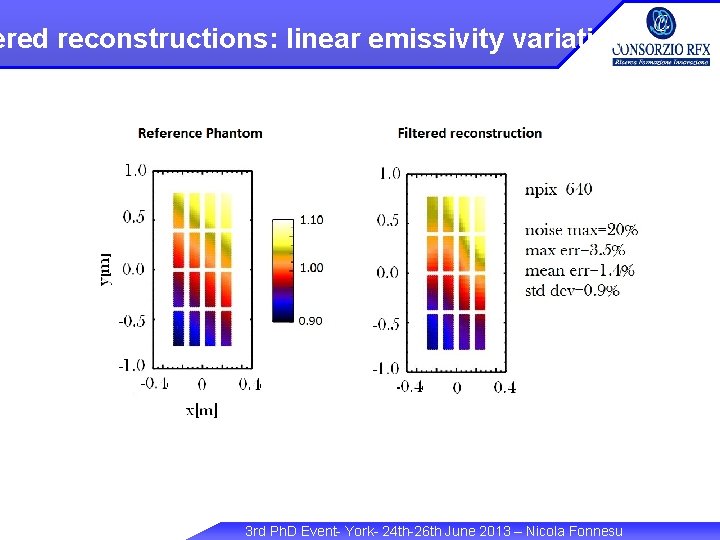
ered reconstructions: linear emissivity variation 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu

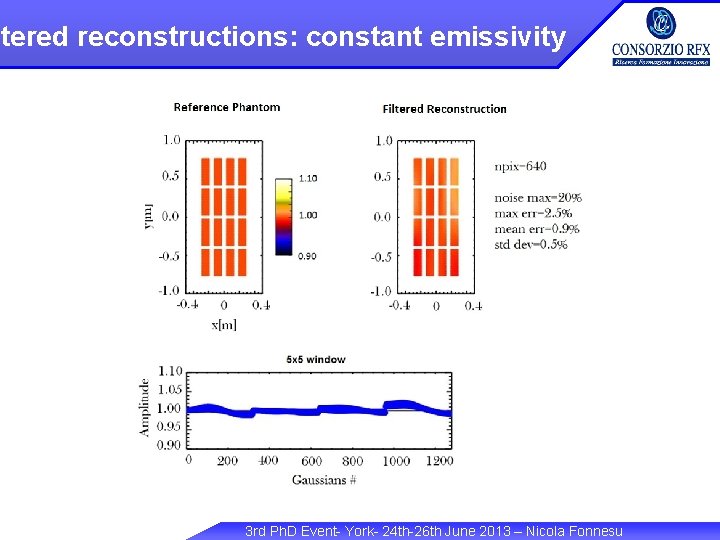
ltered reconstructions: constant emissivity 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu

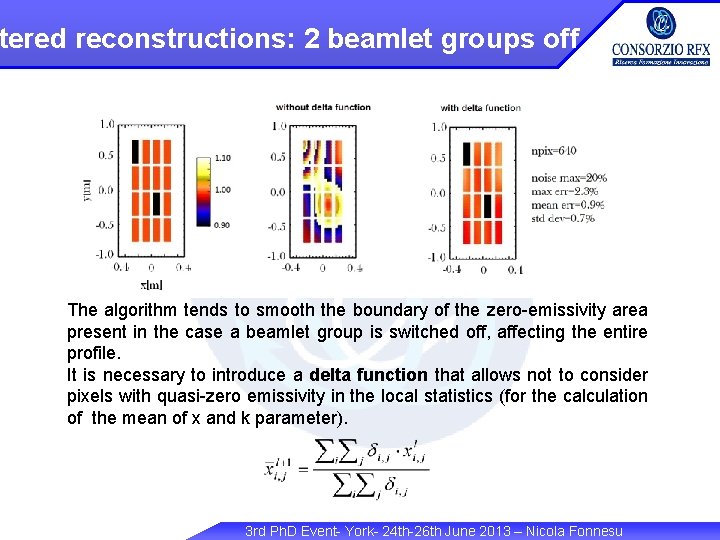
tered reconstructions: 2 beamlet groups off The algorithm tends to smooth the boundary of the zero-emissivity area present in the case a beamlet group is switched off, affecting the entire profile. It is necessary to introduce a delta function that allows not to consider pixels with quasi-zero emissivity in the local statistics (for the calculation of the mean of x and k parameter). 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu

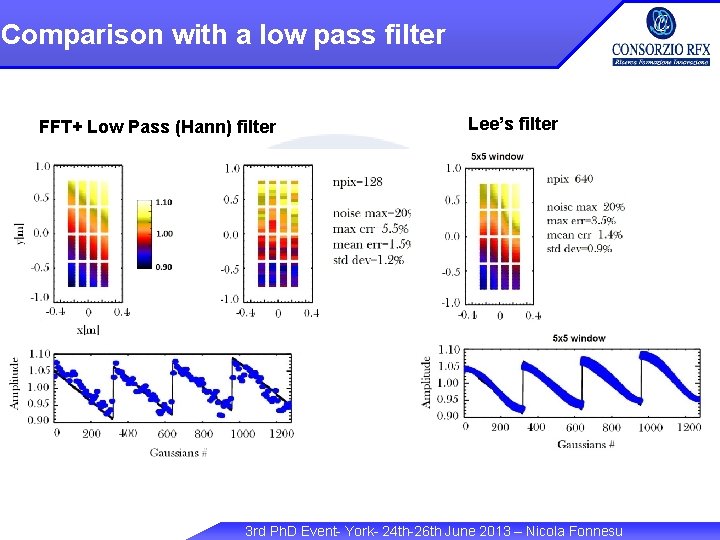
Comparison with a low pass filter FFT+ Low Pass (Hann) filter Lee’s filter 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu

Conclusions • The maximum errors (in reconstructions with 640 pixels) are reduced to values up to 3. 5% considering different operating conditions of SPIDER. • Filtering in the spatial frequency domain could give similar results (for the same level of noise) just considering a lower number of pixels (i. e. 32 or 64). • A higher number of pixels can go beyond the simple detection of the lack of uniformity of the beam, giving information about its causes and suggesting possible solutions. • Encouraging attempt to demonstrate the feasibility to suppress instrumental noise by a post-processing algorithm that does not increase significantly the processing time. 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu

Future Works • Filtering algorithm for MITICA visible tomography • Development of the tomography code for N 1 O (60 k. V negative ion source) 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu

THANK YOU FOR YOUR ATTENTION ! 3 rd Ph. D Event- York- 24 th-26 th June 2013 – Nicola Fonnesu