An Extended Structure Model for Massive Galactic Cores

Overview • Introduction • The Model • Computational Strategy • Results • Discussion •

Introduction • Measurements of the size of the central radio source Sgr. A* and

The Model The equations for the dark matter model are written as follows: ;

The Model (cont’d) Potential: Pressure: Density :

The Model (cont’d) The quantities appearing in the above equations are related to the

Computational Strategy Initially Set: • K(0), m(0) Metric functions at r=0 • Mass of

Einstein Metric Functions 1. 20 E+00 1. 00 E+00 8. 00 E-01 6. 00

Density 3. 50 E+00 grams/cm^3 3. 00 E+00 2. 50 E+00 2. 00 E+00

grams Mass Function 1. 00 E+44 1. 00 E+40 1. 00 E+36 1. 00

Stellar Velocity 1. 00 E+11 1. 00 E+10 cm/sec 1. 00 E+09 1. 00

Test Particle Geodesic Trajectories Breakup occurs if = 3 x 10^-7 (sun) =3 (white

Tidal Forces cm Radial Position 1. 00 E+16 1. 00 E+15 1. 00 E+14

Discussion • Model Fits Data for most compact source candidate (1. 3 mm microwave;

Summary and Conclusions • Measured properties (mass and apparent size) of the stellar object

The Debate: Modified Gravity or Dark Matter? • Is dark matter simply a fudge

Slides: 16

Download presentation

An Extended Structure Model for Massive Galactic Cores T. Wilcox, UCLA Miami 2011

Overview • Introduction • The Model • Computational Strategy • Results • Discussion • Summary • Conclusions

Introduction • Measurements of the size of the central radio source Sgr. A* and motions of orbiting stars have been considered compelling evidence for the existence of a black hole of some 4. 4 million solar masses at the center of our galaxy. • An alternative that meets observational constraints is the possible existence of a gravitationally bound distribution of dark matter in the form of a fermion gas • The general relativistic model presented here includes an equation of state that predicts a fermion mass of 150 kev.

The Model The equations for the dark matter model are written as follows: ;

The Model (cont’d) Potential: Pressure: Density :

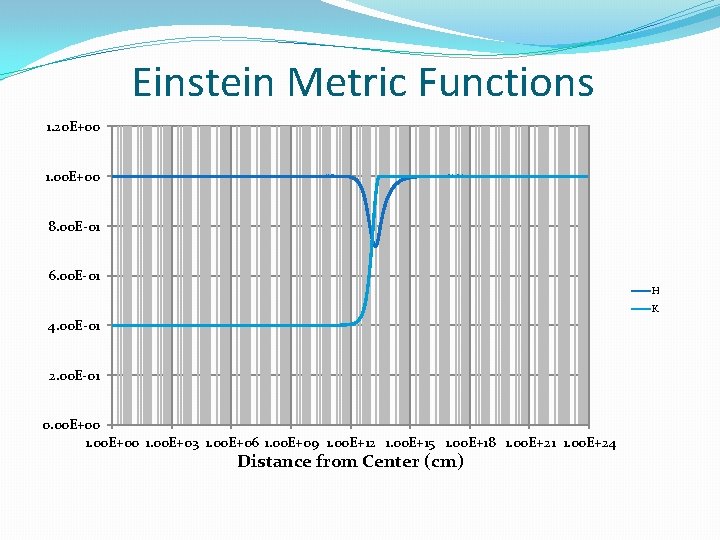
The Model (cont’d) The quantities appearing in the above equations are related to the standard metric of general relativity as follows: Boundary Conditions: ; ;

Computational Strategy Initially Set: • K(0), m(0) Metric functions at r=0 • Mass of dark fermion • Parameter (Required for correct boundary condition at large r) • Integrate outward from zero

Einstein Metric Functions 1. 20 E+00 1. 00 E+00 8. 00 E-01 6. 00 E-01 H K 4. 00 E-01 2. 00 E-01 0. 00 E+00 1. 00 E+03 1. 00 E+06 1. 00 E+09 1. 00 E+12 1. 00 E+15 1. 00 E+18 1. 00 E+21 1. 00 E+24 Distance from Center (cm)

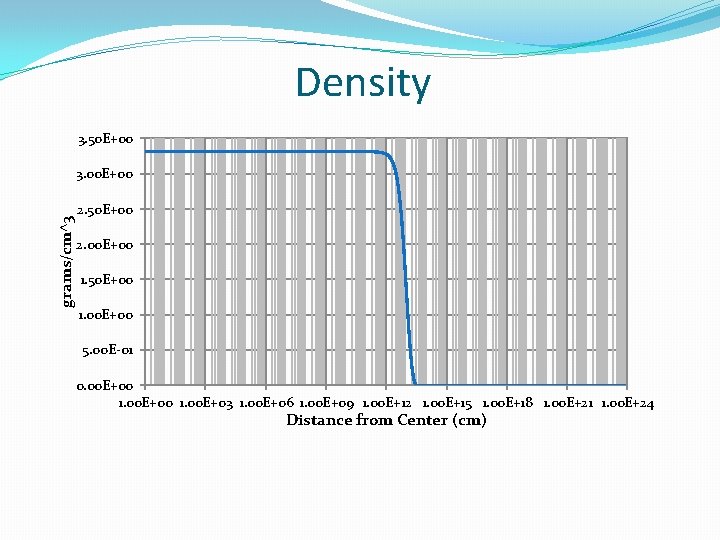
Density 3. 50 E+00 grams/cm^3 3. 00 E+00 2. 50 E+00 2. 00 E+00 1. 50 E+00 1. 00 E+00 5. 00 E-01 0. 00 E+00 1. 00 E+03 1. 00 E+06 1. 00 E+09 1. 00 E+12 1. 00 E+15 1. 00 E+18 1. 00 E+21 1. 00 E+24 Distance from Center (cm)

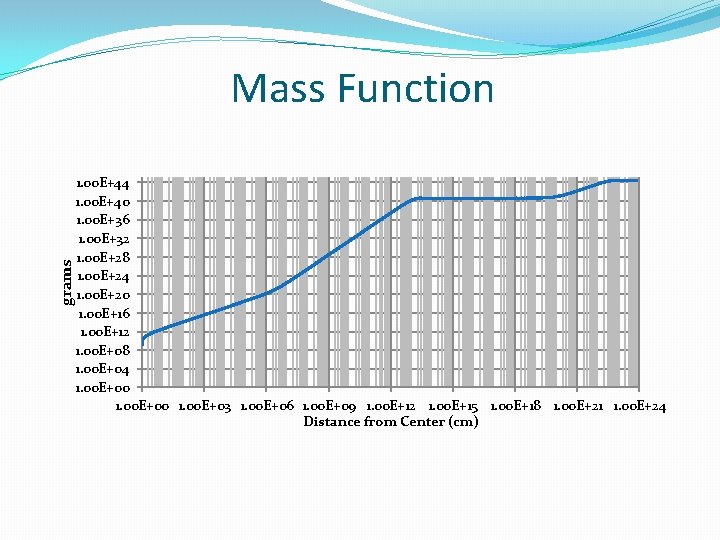
grams Mass Function 1. 00 E+44 1. 00 E+40 1. 00 E+36 1. 00 E+32 1. 00 E+28 1. 00 E+24 1. 00 E+20 1. 00 E+16 1. 00 E+12 1. 00 E+08 1. 00 E+04 1. 00 E+00 1. 00 E+03 1. 00 E+06 1. 00 E+09 1. 00 E+12 1. 00 E+15 1. 00 E+18 1. 00 E+21 1. 00 E+24 Distance from Center (cm)

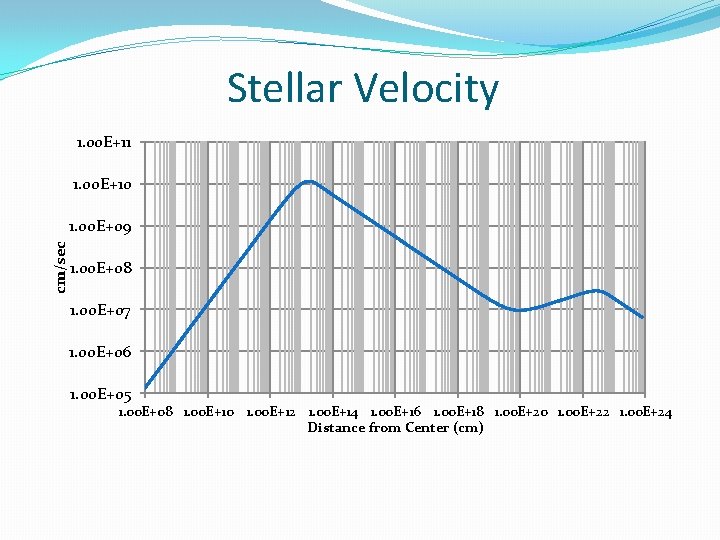
Stellar Velocity 1. 00 E+11 1. 00 E+10 cm/sec 1. 00 E+09 1. 00 E+08 1. 00 E+07 1. 00 E+06 1. 00 E+05 1. 00 E+08 1. 00 E+10 1. 00 E+12 1. 00 E+14 1. 00 E+16 1. 00 E+18 1. 00 E+20 1. 00 E+22 1. 00 E+24 Distance from Center (cm)

Test Particle Geodesic Trajectories Breakup occurs if = 3 x 10^-7 (sun) =3 (white dwarf) = 3 x 10^5 (neutron star)

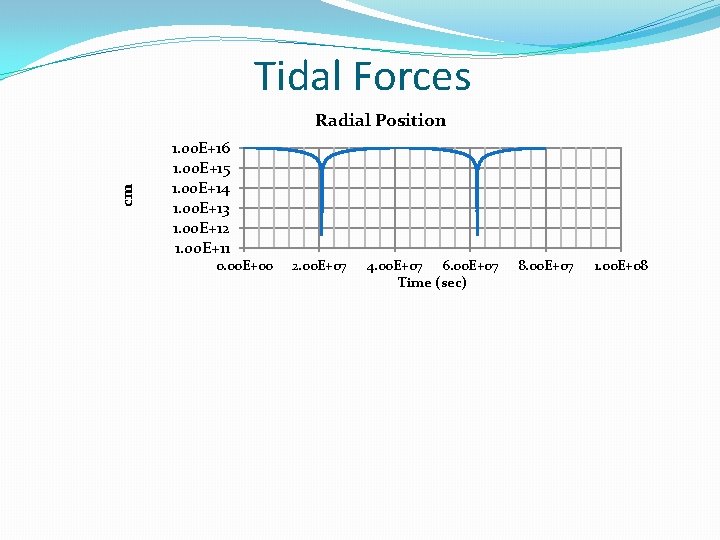
Tidal Forces cm Radial Position 1. 00 E+16 1. 00 E+15 1. 00 E+14 1. 00 E+13 1. 00 E+12 1. 00 E+11 0. 00 E+00 2. 00 E+07 4. 00 E+07 6. 00 E+07 Time (sec) 8. 00 E+07 1. 00 E+08

Discussion • Model Fits Data for most compact source candidate (1. 3 mm microwave; site is colocated with Sgr. A*) • Core mass of 4. 4 x 10^6 solar masses • Distribution of matter is mechanically stable • Degenerate Fermi gas • Beyond the edge of degenerate region density falls abruptly (depends weakly on temperature) • Total mass (within volume of radius “r”) plateaus beyond radius of about 1. 4 AU out to about 1 kpc • Forms “atmosphere” mixed with visible matter • Drops off beyond 30 kpc (outer limit of ordinary matter) • If temperature sufficiently high total mass of dark matter increases without bound

Summary and Conclusions • Measured properties (mass and apparent size) of the stellar object at the galactic center (Sgr. A*) can be fitted to a gravitationally bound fermi gas model that describes principle features of the massive core. • Stellar velocity curves fit observed forms in both the inner (100 -1000 AU) and outer (1 -30 kpc) galactic regions. • The two parameters of the model that generate the fit are the mass of the fermion and the density of dark matter at r=0. • The density of dark matter is virtually independent of temperature, provided the value does not exceed approximately degrees. • The model predicts the mass of the dark matter particle to be approximately. 2 electron masses.

The Debate: Modified Gravity or Dark Matter? • Is dark matter simply a fudge to “correct” the Newtonian law of gravity? - Co-evolution with normal matter; are they separable? * Must the distribution must be set in each instance? - Dissipative processes, what are they? * Can a concentration of dark matter “collapse” without them? * Gravitational scattering by large masses * If all else fails—dissipation via massless dark “photons” • Modified gravity: is it a truly “universal” i. e. , one (or perhaps a few) parameters to be set once and for all? -Gravitational lensing -Colliding galaxies