An Explanation of the Different Forms of Quadratic

An Explanation of the Different Forms of Quadratic Functions Gee, I’m puzzled! By Katie Johnson

Ralph is puzzled. What is a quadratic function anyway? The parent function of a quadratic function is y = x 2 Its graph is a parabola with an axis of symmetry which is parallel to the y-axis. A quadratic function can be written in Standard Form, Vertex Form, and Intercept Form.

Standard Form Standard form is written as: f(x) = ax 2 + bx + c The value of “a” tells us whether the parabola will open up or down. If “a” is positive, the graph will open up, and if it is negative, the graph will open down. We also know that “c” is the y-intercept of the graph. But what we don’t know yet are the coordinates of the vertex. Before we can graph a quadratic function in standard form, we need to find the vertex. This can be done by dividing the opposite of “b” by 2 a, or (-b/2 a). This value is the x-coordinate of the vertex. When we plug this value into the function for x, we find the ycoordinate. Now we have the vertex, or (-b/2 a, f(-b-2 a)).

Graphing in Standard Form Once the vertex has been plotted, one can plot the axis of symmetry. The axis of symmetry is simply a vertical line through the vertex, and its equation is simply x set equal to the x-coordinate of the vertex. For example, if the vertex were (-2 , 3), the equation of the axis of symmetry would be x = -2. Now that we have these plotted, we need at least two more points on the graph so that we can find the curve of the parabola. One of these points will be (0, c), because “c” is the y-intercept of the graph! To find the other point, one could easily find the distance between (0, c) and the axis of symmetry (horizontally) and continue that distance equally on the other side of the axis, where the second point could be plotted. …Hence the name axis of symmetry. Now, we can connect the points in a smooth curve and the graph is complete.

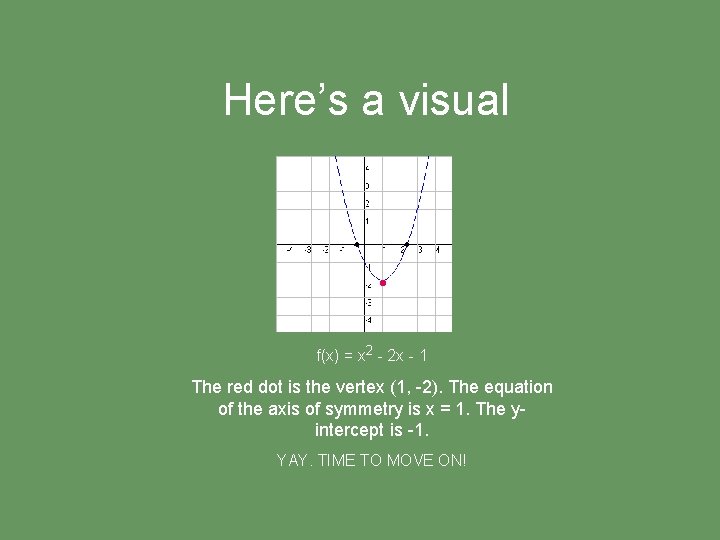
Here’s a visual • f(x) = x 2 - 2 x - 1 The red dot is the vertex (1, -2). The equation of the axis of symmetry is x = 1. The yintercept is -1. YAY. TIME TO MOVE ON!

Vertex Form Vertex form is written as: f(x) = a (x - h) 2 + k In vertex form, “a” still tells us whether the parabola will open up or down, but the other variables give us different information. “h” tells us how far left or right the parabola is on the graph, “k” tells us how far up or down it is, and the vertex of the parabola is (h , k). This can making graphing a quadratic function simpler because we don’t have to do any work to find the parabola - it’s given to us in the function.

Graphing in Vertex Form We already have the vertex (h , k) and the axis of symmetry is x = h. Now to graph, we just need to find the two points. To do this, one could plug any value (i. e. 0, 1, 2) into the function for x and call the resulting value y and use this as a point, but another easy trick is to move one unit to the left and to the right of the vertex and then move up or down according to the value of “a”. That is, if the vertex were (1, 0) and “a” was 3, the two resulting points would be (0, 3) and (2, 3). Now all that’s left to do is connect the points.

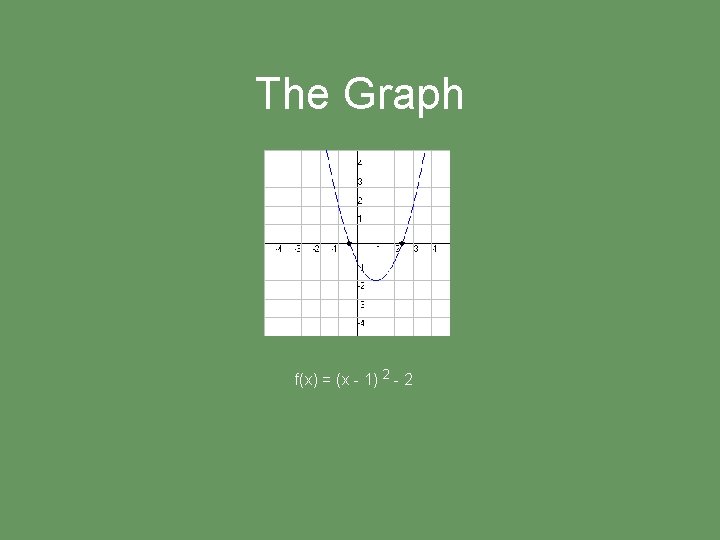
The Graph f(x) = (x - 1) 2 - 2

Intercept Form Intercept form is written as: f(x) = a (x-p)(x-q) In this form, “a” is the same, and “p” and “q” are the x-intercepts of the parabola. This makes graphing pretty easy because after we plot (p , 0) and (q , 0), all we need to do is find the vertex. The vertex can be found by adding p and q and then dividing by 2. This is the x-coordinate. To find the y-coordinate, this value is plugged into the function. So, the vertex is ((p+q)/2, f((p+q)/2)). This means that the equation of the axis of symmetry is x = (p+q)/2.

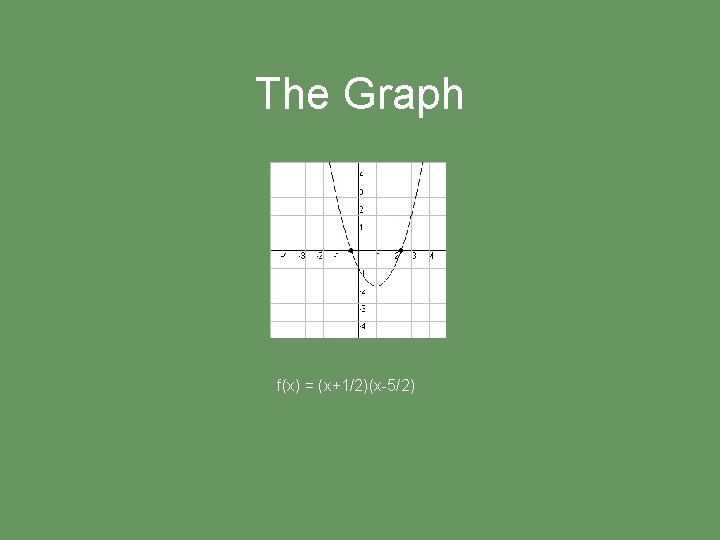
The Graph f(x) = (x+1/2)(x-5/2)

Hey, now you know all about graphing a quadratic function in each form! Gee whiz, now I get it!