An Example of Stepwise Refinement of Distributed Programs

An Example of Stepwise Refinement of Distributed Programs: Quiescence Detection Author: MANI CHANDY and JAYADEV MISRA Presenter: Qing Bao Bei Di Chen Yi Ling Yang Zuojian Tang Zongyan Wang

Outline • Introduction • Specification of Detection Problems • Refinement for Distributed System Architecture • Conclusion

Section 1. Introduction • What do we propose? – Methodology: • For the development of concurrent program • Based on a novel view of what a program is – Traditional view: program = input + {instruction} + output – Our view: program = an initial condition + {atomic state. } – Computation State view: program = declaration of variables and their initial values + {multiple assignments} – Example: • Quiescence Detection : termination or deadlock

Introduction • Key Features of the CPM (Concurrency Programming Methodology): – Core problem separates concurrency HW/SW – A global view at early stages of design – Reasoning based on properties – predicates • Benefits of Applying it to Quiescence Detection Algorithms We obtain the weakest conditions under which the algorithms can operate, such as the concrrent architecuters, detection orders, detection interval.

Desiderata for a CPM • Separating Concerns About the Core Problem from Details About Concurrency – It is possible and important to separate them because concurrency is less well understood – The ideas that form the foundation of good programming transcend different forms of concurrency employed in diff. Implementation – Programs outlive the architecture for which they were initially designed

Desiderata of a CPM • Process-Eye View versus a Global Perspective – In the initial stage, we may not know what processes to employ; we are force to take a global view at this stage • Reasoning About Unchanging System Properties versus Operations Reasoning – Operational reasoning is more difficult because it is harder to understand unfolding histories of actions – A danger with Operational reasoning is that some actions may be missed, while the proof needs all

Specifications • In terms of Predicates on system states e. g. , “n is even”, “system P is idle” • Some notations and terms: – {u}t{v} : u, v : predicate; t: statement. Means: if u holds before t, after t, v holds. e. g. u = “n is even”, t = {n = n+1}, v = “n is odd” – An Invariant Predicate I means • • I is true initially {I}t{I} for all t eg I = “ 3 is a prime” I is an invariant

Specifications • A binary relation → between predicates: u → v holds for a program ≡ (1 a) {u and not v} t {u or v} for all t , and (1 b) Exists t, such that {u and not v} t {v} or (2) Some predicates w, (u →w) and (w →v) (transition) u→v holds: if u holds, within finite time, v holds. Eg u=“p is in a deadlock”, v=“free is false”

Heuristics, Model • Heuristics – Freely choose variables to formulate a solution at early design phase – Generalize predicates on system to on subsystem to direct the next refinement – Exploit locality of interactions in predicates • Model – Retain features mentions before – Specification in terms of Invariance/Progress(→)

Consequences Features Wanted How the model achieves 1. Separate the core system form the concurrency form 2. Reasoning based on a global view • Uniform view of programs • Independent of architecture 3. Reasoning based on system properties • Avoid all forms of sequencing • Focus on the total system at a refinement step Derive programs for diverse architectures.

Section 2: Specification of Detection Problems General Form of Detection Quiescence Detection

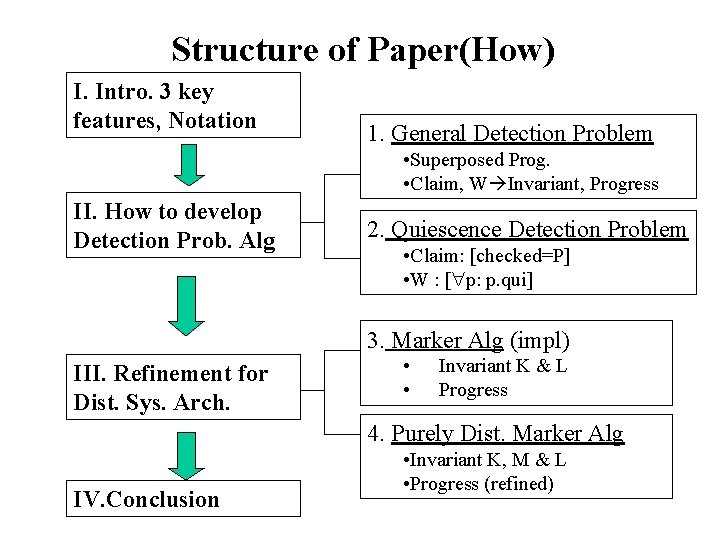
Structure of Paper(How) I. Intro. 3 key features, Notation 1. General Detection Problem • Superposed Prog. • Claim, W Invariant, Progress II. How to develop Detection Prob. Alg 2. Quiescence Detection Problem • Claim: [checked=P] • W : [ p: p. qui] 3. Marker Alg (impl) III. Refinement for Dist. Sys. Arch. • • Invariant K & L Progress 4. Purely Dist. Marker Alg IV. Conclusion • Invariant K, M & L • Progress (refined)

General Form of Detection Given: • A Underlying Program • Predicate W on the underlying program v W is preserved by the underlying program Need Superposition Superpose a program on the underlying program Get a Superposed Program • • Could record but not affect the underlying computation Could employ new variables

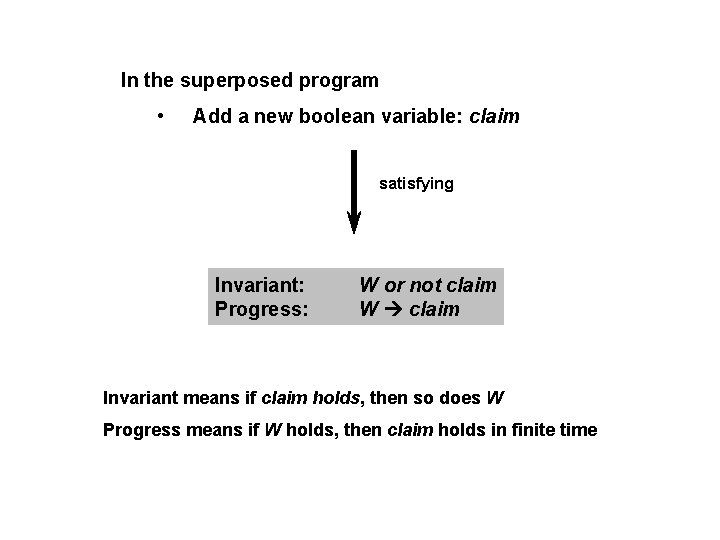
In the superposed program • Add a new boolean variable: claim satisfying Invariant: Progress: W or not claim W claim Invariant means if claim holds, then so does W Progress means if W holds, then claim holds in finite time

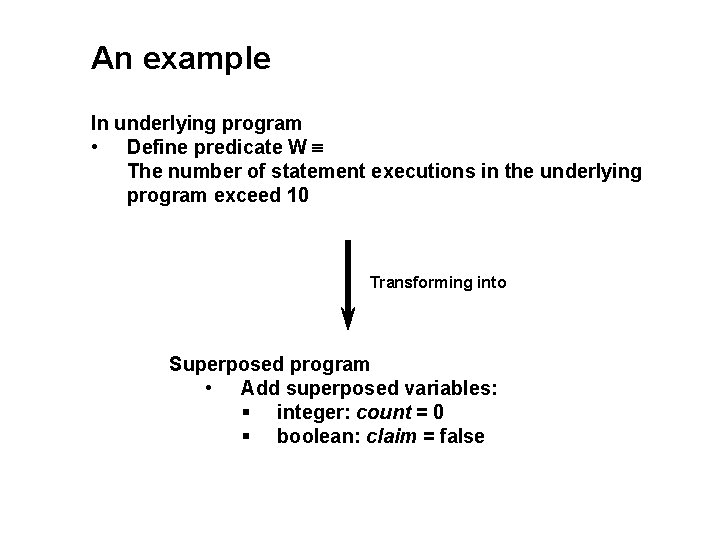
An example In underlying program • Define predicate W The number of statement executions in the underlying program exceed 10 Transforming into Superposed program • Add superposed variables: § integer: count = 0 § boolean: claim = false

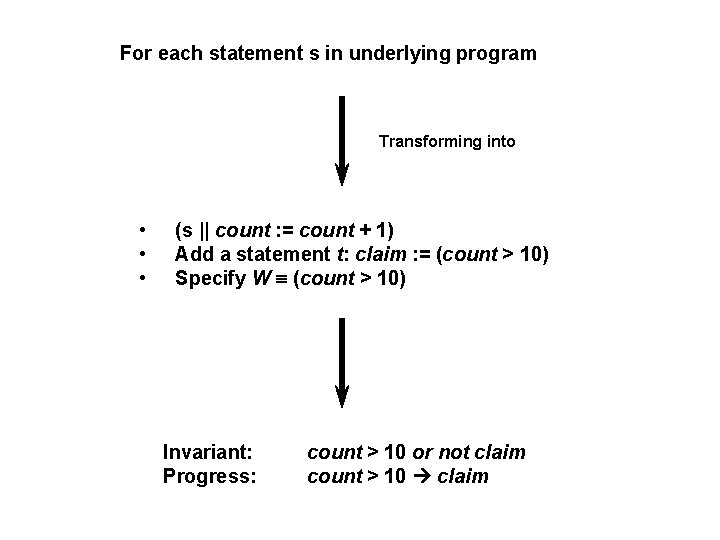
For each statement s in underlying program Transforming into • • • (s || count : = count + 1) Add a statement t: claim : = (count > 10) Specify W (count > 10) Invariant: Progress: count > 10 or not claim count > 10 claim

In the superposed program • For all statements s: {count > 10 and not claim} s {count > 10 or claim} • For statement t: {count > 10 and not claim} t {claim}

Quiescence Detection • • Deal with a specific property W A specific class of underlying programs A concurrent program consisting of a fixed set p of processes Local quiescence property {p. qui and [ q such that q affects p: q. qui]} t {p. qui} p. qui is a predicate associating with each p affects is a binary relation between processes W [ p: p. qui] (preserved)

Deriving a Program Skeleton Specifications: W [ p: p. qui] Invariant: W or not claim Progress: W claim Initially: claim = false; Statement set: claim : = W

SPECIFICATION OF DETECTION PROBLEMS Stepwise Refinement

HOW? Structure of Paper I. Intro. 3 key features, Notation 1. General Detection Problem • Superposed Prog. • Claim, W Invariant, Progress II. How to develop Detection Prob. Alg 2. Quiescence Detection Problem • Claim: [checked=P] • W : [ p: p. qui] 3. Marker Alg (channel, marker) III. Refinement for Dist. Sys. Arch. • • Invariant K & L Progress 4. Purely Dist. Marker Alg (token) IV. Conclusion • Invariant K, M & L Progress (refined)

Stepwise Refinement • What is Stepwise Refinement? • Why is Stepwise Refinement good? • How does Stepwise Refinement do?

Refinement Step • What we are standing on now? W ≡ [ p: p. qui ] Invariant: W or not claim Progress: W claim • Move to next step

Refinement Step • Introduce a new term, “checked”, which is a set of processes satisfying some condition (we postpone consideration of what this condition should be). • What is the purpose of “checked”?

Refinement Step • Define claim ≡ (checked = P), where P is the set of all processes. • Substitute claim into the Invariant and Progress predicates. Invariant: W or (checked != P) Progress: W (checked = P)

Refinement Step • Since W is system-wide property, next step is to generalize W to a subsystem property w defined on process sets S where S P, such that w(P) ≡ W. • In other words, w(S) ≡ [ p in S: p. qui ]

Refinement Step • Rewrite Invariant and Progress predicates Invariant: w(checked) or (checked != P) Progress: w(P) (checked = P) (Previous Invariant: W or (checked != P)) (Note: W ≡ w(P))

Refinement Step • If p. inc then checked: ={p} checked • Invariant: w(checked) or [ unchecked q: not q. inc] • (Pre Invariant: w(checked) or (checked != P) • Progress: • A) w(P) [ p: p. inc] and • B) [ p: p. inc] checked = P

Refinement Step • Apply the locality of the relation affects. • Invariant: w(checked) or [ unchecked q, checked p: (not q. inc) and (q affects p)] (Pre Invariant: w(checked) or [ unchecked q: not q. inc])

Refinement Step • Invariant: [ checked p: p. qui] or [ unchecked q, checked p: (not q. inc) and (q affects p)] • Strengthen it to Invariant: [ checked p: p. qui and p. inc] or [ unchecked q, checked p: (not q. inc) and (q affects p)]

Setion 3. Refinement for Dist. Sys Arch Objective: Derived A Superposed Program

HOW? Structure of Paper I. Intro. 3 key features, Notation 1. General Detection Problem • Superposed Prog. • Claim, W Invariant, Progress II. How to develop Detection Prob. Alg 2. Quiescence Detection Problem • Claim: [checked=P] • W : [ p: p. qui] 3. Marker Alg (channel, marker) III. Refinement for Dist. Sys. Arch. • • Invariant K & L Progress 4. Purely Dist. Marker Alg (token) IV. Conclusion • Invariant K, M & L Progress (refined)

A Superposed program has a boolean variable claim satisfying: • Invariant: W or not claim • Progress: W claim • W All processes and all msg in all channel are stable • Claim checked=P where P is the set of all processes

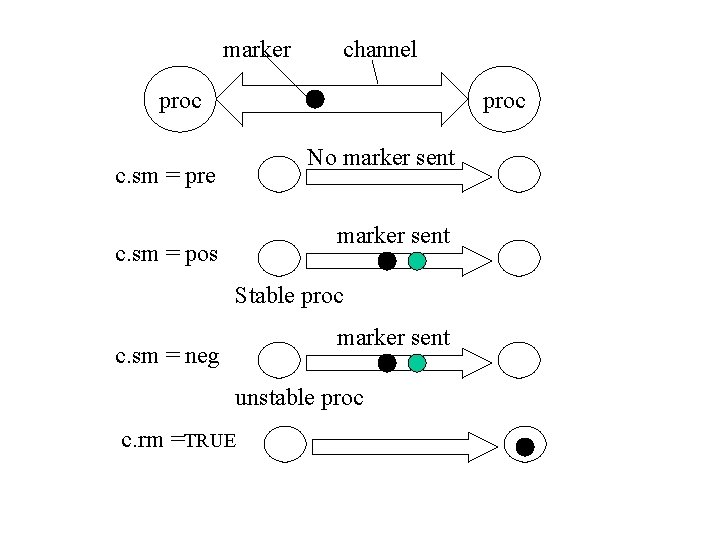
marker channel proc No marker sent c. sm = pre marker sent c. sm = pos Stable proc marker sent c. sm = neg unstable proc c. rm =TRUE

Invariant K ([ p in checked: p. stable] and [ channels c to checked processes: c. rm] and [ channels c to, or from, checked processes: c. sm neg]) Or [ channels c from an unchecked to a checked process: c. sm=neg]

Invariant L (c. num<=1) and not(c. rm and c. num=1) and (c. sm=pre) (c. num=0 and not c. rm) and (c. sm=pos) [ msg m in c: m is stable or there is a marker following m in c]

Progress Condition 1) 2) 3) 4) c. sm=pre c. sm=pos and c. num=1 c. rm W W and [ c: c. sm = pos and c. rm] W and [ c: c. sm=pos and c. rm] checked=P 5) c. sm=neg c. sm = pre

Marker Alg (Superposed Prog) Initially: checked = empty, [ c: c. rm=false and c. sm=pre] Set of statements Marker sending along c: (PC 1) If c. sm=pre then send marker along c || c. sm: =pos Upon receiving marker along c: (PC 2) If marker is received along c then c. rm: =true Upon sending unstable message along c: (K) If c. sm=pos and unstable message send along c then c. sm: =neg

Marker Alg (cont’) Reinitializing c: If c. sm=neg and c. rm and c is from an unchecked to an unchecked process then begin c. sm: =pre || c. rm: =false Reinitializing c and checked: If c. sm = neg and c. rm and c is from an unchecked to a checked process then begin checked: =empty || c. sm : =pre || c. rm: =false Adding q to checked: If q. stable and [ input channels c of q: c. rm] and [ output channels c of q: c. sm neg] then checked: {q} checked

HOW? Structure of Paper I. Intro. 3 key features, Notation 1. General Detection Problem • Superposed Prog. • Claim, W Invariant, Progress II. How to develop Detection Prob. Alg 2. Quiescence Detection Problem • Claim: [checked=P] • W : [ p: p. qui] 3. Marker Alg (channel, marker) III. Refinement for Dist. Sys. Arch. • • Invariant K & L Progress 4. Purely Dist. Marker Alg (token) IV. Conclusion • Invariant K, M & L Progress (refined)

Invariant K (refined) ([ p in checked: p. stable] and [ c between checked processes: c. stable] and [ c from, checked processes: c. sm=pos]) Or [ c from unchecked to checked process: c. sm=neg]

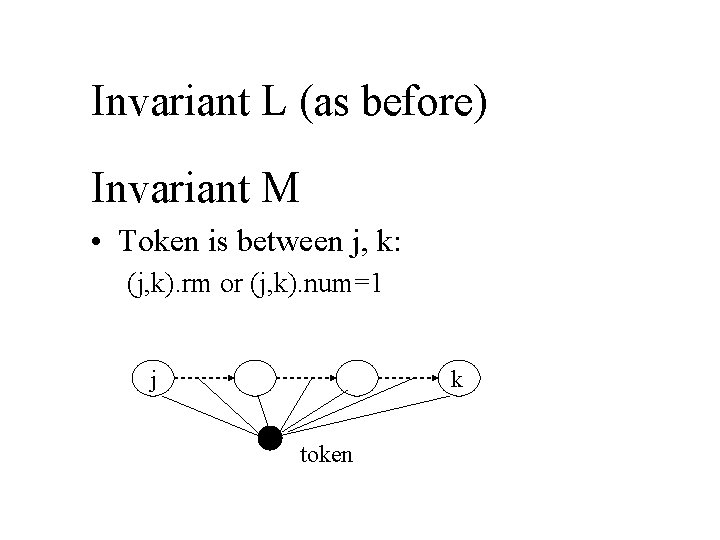
Invariant L (as before) Invariant M • Token is between j, k: (j, k). rm or (j, k). num=1 j k token

Progress Condition (refined) • For all sets of channels C and all processes I: W and I. holdstoken and [ c in C: c. sm=pos] W and (I+1). holdstoken and [ c in C’: c. sm=pos] Where C’ = c {c|c is an output channel of process I} • For all sets of processes Q and all processes I: W and I. holdstoken and [ c: c. sm=pos] and [ q in Q: q checked] W and (I+1). holdstoken and [ c: c. sm=pos] [ q in Q’: q checked] Where Q’=Q {I} and

Alg. For Progress I, • If I. holdstoken and I. stable and [ input channels c of I: c. rm] then begin – Send token to (I+1) mod n with checked as follows: • If[ channels (I, j) to checked j: (I, j). sm neg] – then checked: =checked {I} • else checked: =empty – || I. holdstoken: =false – || [for all input channels c of I: c. rm: =false] – || [for all output channels c of I: send marker along c || c. sm: =pos] • End

Alg (cont’) Upon process I receiving the token: If I receives the token then I. holdstoken : =true Upon process I receiving marker along c: If marker is received along c then c. rm: =true Upon process I sending unstable message along c: If c. sm=pos and unstable message sent along c then c. sm=neg

Initial Condition • I. holdstoken: (I=0) {token is at process 0}; • For a channel c from a process I to a process j, for all I, j: c. rm =(I>j) • No channel contains a marker (I. e. , for all c: c. num=0); • For all channels c: c. sm=neg • Checked = empty

Section 4. Conclusion WHAT? METHODOLOGY(for developing concurrent prog) Concurrent Prog others Quiescence Detect Alg

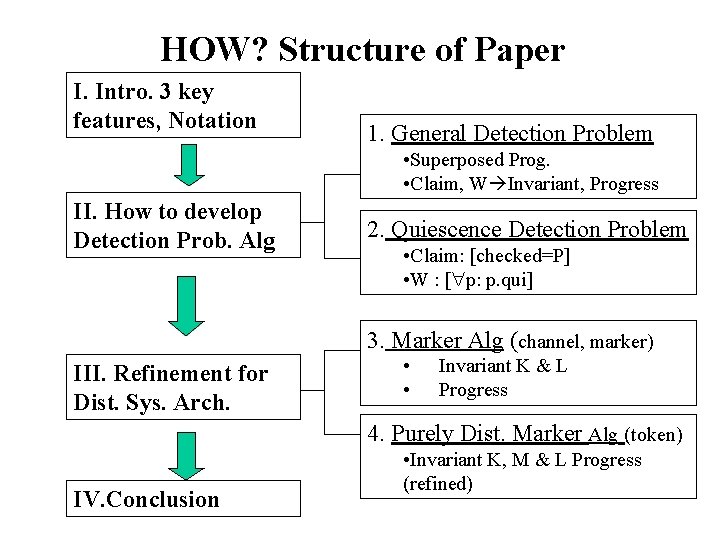
HOW? Structure of Paper I. Intro. 3 key features, Notation 1. General Detection Problem • Superposed Prog. • Claim, W Invariant, Progress II. How to develop Detection Prob. Alg 2. Quiescence Detection Problem • Claim: [checked=P] • W : [ p: p. qui] 3. Marker Alg (channel, marker) III. Refinement for Dist. Sys. Arch. • • Invariant K & L Progress 4. Purely Dist. Marker Alg (token) IV. Conclusion • Invariant K, M & L Progress (refined)

Benefit of Methodology (Why) 1. Very General 2. Separate concerns between • core problem to be solved and • details of concurrency in different arch. 3. Focus on levels of detail of arch. at one refinement 4. Original! A BEAUTIFUL MIND?

Question?