An Exact Algorithm for Coupling Free Routing Ryan

An Exact Algorithm for Coupling -Free Routing Ryan Kastner, Elaheh Bozorgzadeh, Majid Sarrafzadeh {kastner, elib, majid}@cs. ucla. edu Embedded and Reconfigurable Systems Group Computer Science Department UCLA Los Angeles, CA 90095 ISPD: Sonoma County, CA, April, 2001 1 ER Group @ UCLA

Outline l l l Basic definitions Coupling-Free Routing Decision Problem (CFRDP) Implication graph Maximum Coupling-Free Layout (MAX-CFL) Conclusion ISPD: Sonoma County, CA, April, 2001 2 ER Group @ UCLA

Coupling l l Definition - capacitance between adjacent wires Deep submicron trends: l l Interconnect has more dominant role Scale wire height at slow rate compared to width smaller device sizes Coupling can account for up to 70% of interconnect capacitance even in. 25 micron designs ISPD: Sonoma County, CA, April, 2001 3 ER Group @ UCLA

Simplify definition of coupling l l Pair-wise boolean relationship between any 2 nets Easy to generalize to non-boolean, makes algorithm more complex length > l distance < d Two wires couple if distance < d and length > l Two wires couple if Cc(i, j) > threshold ISPD: Sonoma County, CA, April, 2001 4 ER Group @ UCLA

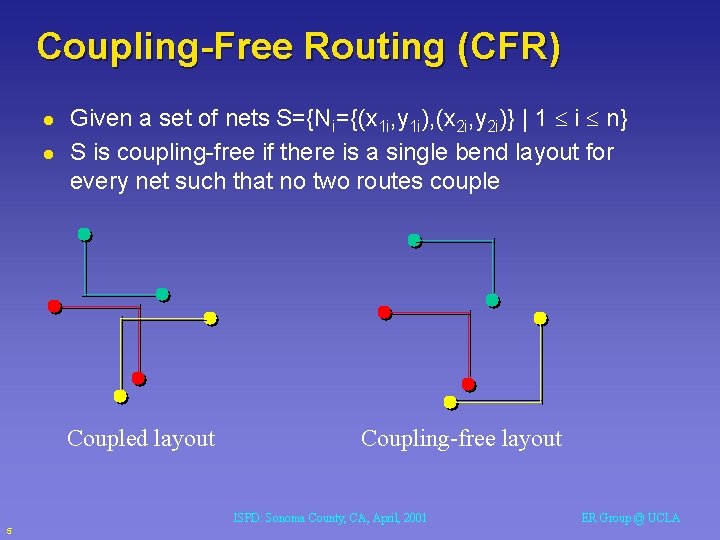
Coupling-Free Routing (CFR) l l Given a set of nets S={Ni={(x 1 i, y 1 i), (x 2 i, y 2 i)} | 1 i n} S is coupling-free if there is a single bend layout for every net such that no two routes couple Coupled layout Coupling-free layout ISPD: Sonoma County, CA, April, 2001 5 ER Group @ UCLA

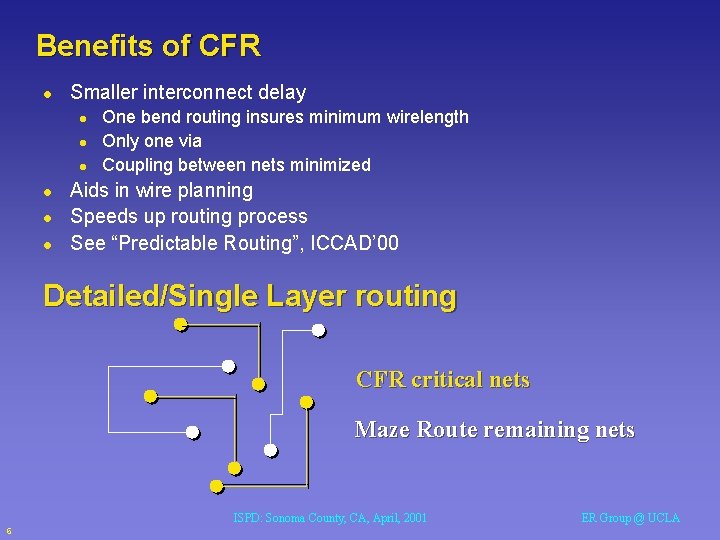
Benefits of CFR l Smaller interconnect delay l l l One bend routing insures minimum wirelength Only one via Coupling between nets minimized Aids in wire planning Speeds up routing process See “Predictable Routing”, ICCAD’ 00 Detailed/Single Layer routing CFR critical nets Maze Route remaining nets ISPD: Sonoma County, CA, April, 2001 6 ER Group @ UCLA

CFR in Global Routing l Coupling at global routing is hard to determine l l Routes are not exact, makes it difficult to know adjacency relations of nets Detailed router will often make local changes Global routing allows global changes, it is very hard to make global changes at the detailed stage Coupling-avoidance in congested areas very important A coupling-free global layout will produce a coupling-free detailed layout ISPD: Sonoma County, CA, April, 2001 7 ER Group @ UCLA

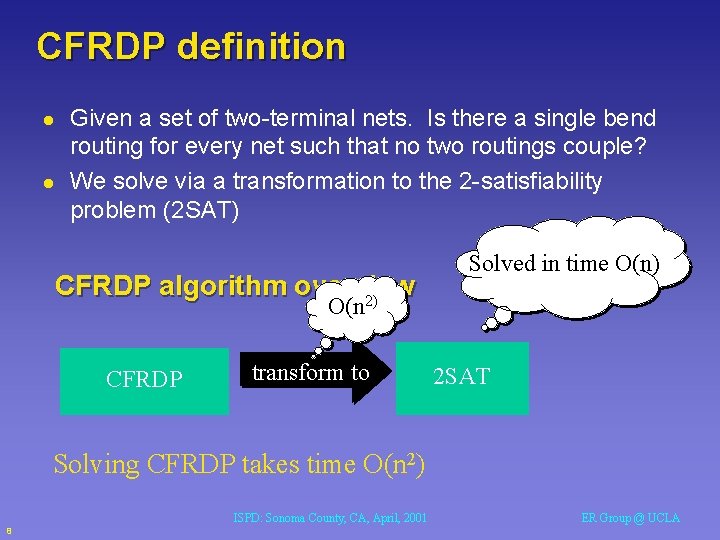
CFRDP definition l l Given a set of two-terminal nets. Is there a single bend routing for every net such that no two routings couple? We solve via a transformation to the 2 -satisfiability problem (2 SAT) CFRDP algorithm overview 2) Solved in time O(n) O(n CFRDP transform to 2 SAT Solving CFRDP takes time O(n 2) ISPD: Sonoma County, CA, April, 2001 8 ER Group @ UCLA

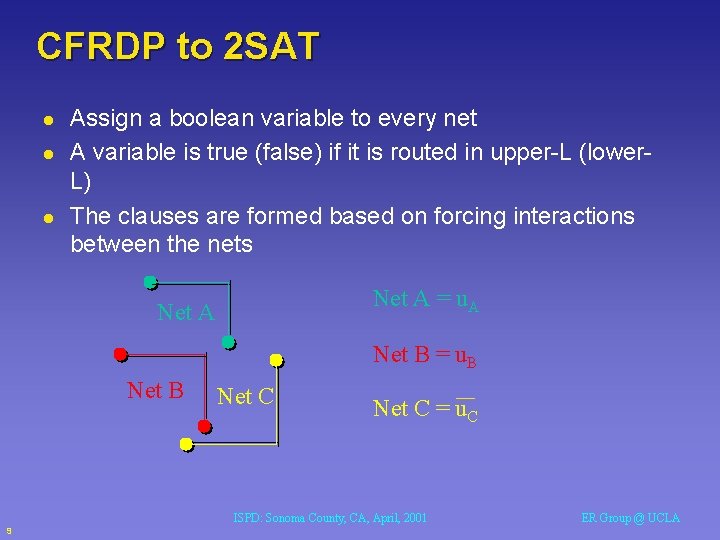
CFRDP to 2 SAT l l l Assign a boolean variable to every net A variable is true (false) if it is routed in upper-L (lower. L) The clauses are formed based on forcing interactions between the nets Net A = u. A Net B = u. B Net C = u. C ISPD: Sonoma County, CA, April, 2001 9 ER Group @ UCLA

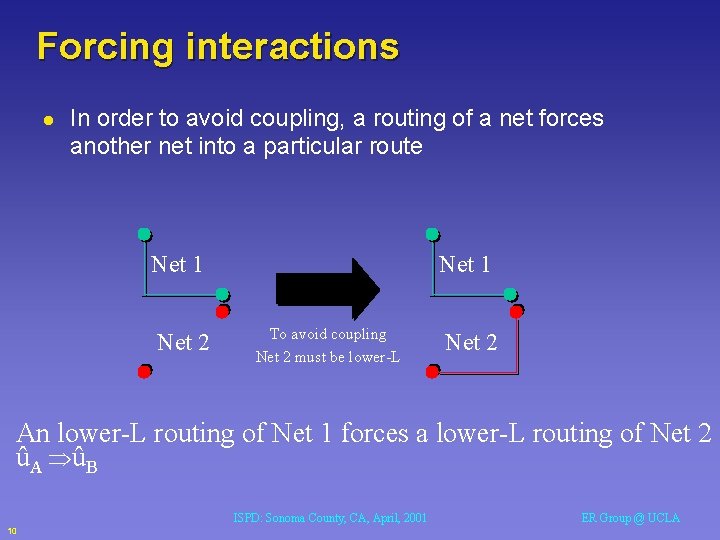
Forcing interactions l In order to avoid coupling, a routing of a net forces another net into a particular route Net 1 Net 2 Net 1 To avoid coupling Net 2 must be lower-L Net 2 An lower-L routing of Net 1 forces a lower-L routing of Net 2 ûA ûB ISPD: Sonoma County, CA, April, 2001 10 ER Group @ UCLA

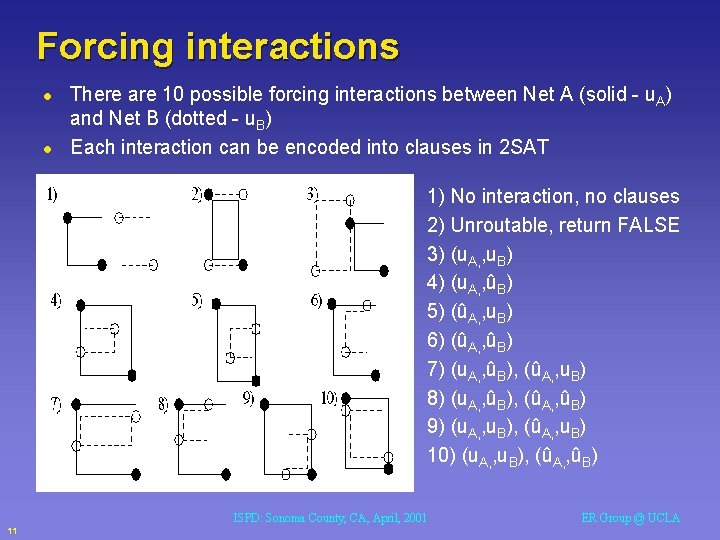
Forcing interactions l l There are 10 possible forcing interactions between Net A (solid - u. A) and Net B (dotted - u. B) Each interaction can be encoded into clauses in 2 SAT 1) No interaction, no clauses 2) Unroutable, return FALSE 3) (u. A, , u. B) 4) (u. A, , ûB) 5) (ûA, , u. B) 6) (ûA, , ûB) 7) (u. A, , ûB), (ûA, , u. B) 8) (u. A, , ûB), (ûA, , ûB) 9) (u. A, , u. B), (ûA, , u. B) 10) (u. A, , u. B), (ûA, , ûB) ISPD: Sonoma County, CA, April, 2001 11 ER Group @ UCLA

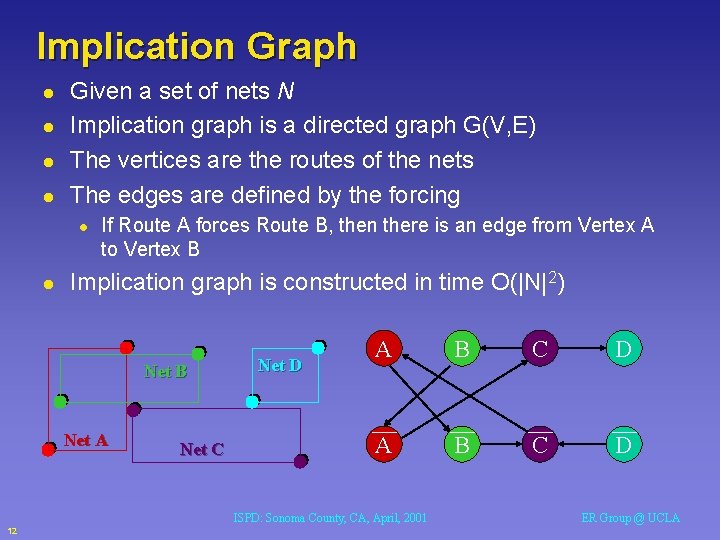
Implication Graph l l Given a set of nets N Implication graph is a directed graph G(V, E) The vertices are the routes of the nets The edges are defined by the forcing l l If Route A forces Route B, then there is an edge from Vertex A to Vertex B Implication graph is constructed in time O(|N|2) Net B Net A Net C Net D A B C D ISPD: Sonoma County, CA, April, 2001 12 ER Group @ UCLA

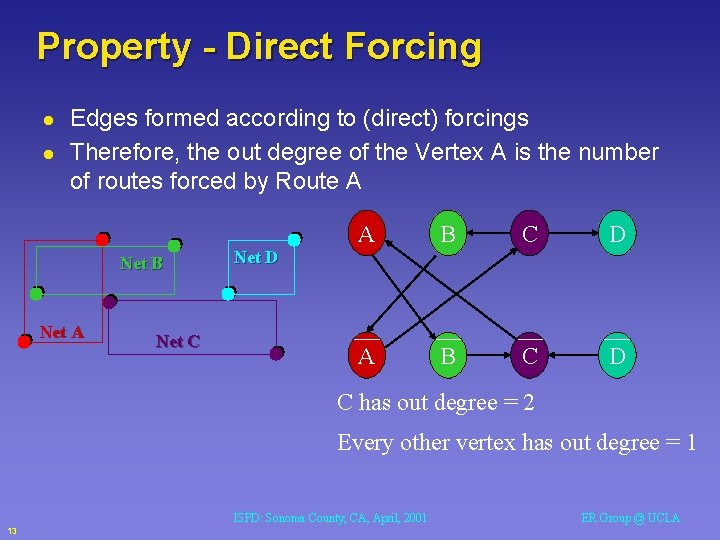
Property - Direct Forcing l l Edges formed according to (direct) forcings Therefore, the out degree of the Vertex A is the number of routes forced by Route A Net B Net A Net C A B C D Net D C has out degree = 2 Every other vertex has out degree = 1 ISPD: Sonoma County, CA, April, 2001 13 ER Group @ UCLA

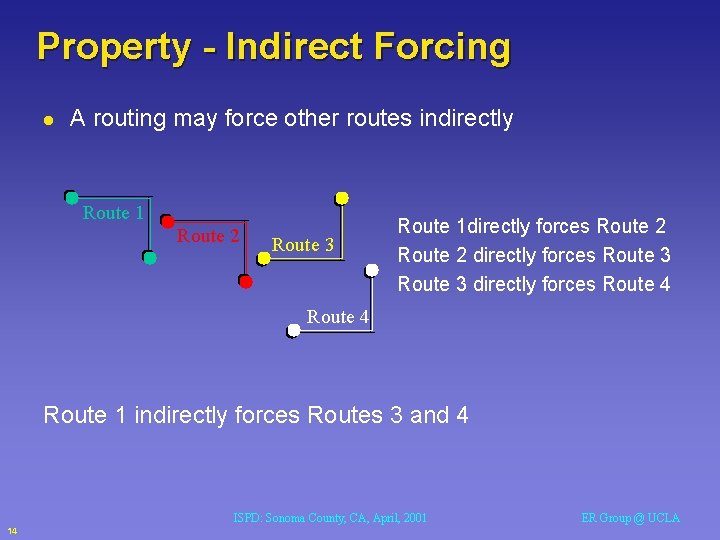
Property - Indirect Forcing l A routing may force other routes indirectly Route 1 Route 2 Route 3 Route 1 directly forces Route 2 directly forces Route 3 directly forces Route 4 Route 1 indirectly forces Routes 3 and 4 ISPD: Sonoma County, CA, April, 2001 14 ER Group @ UCLA

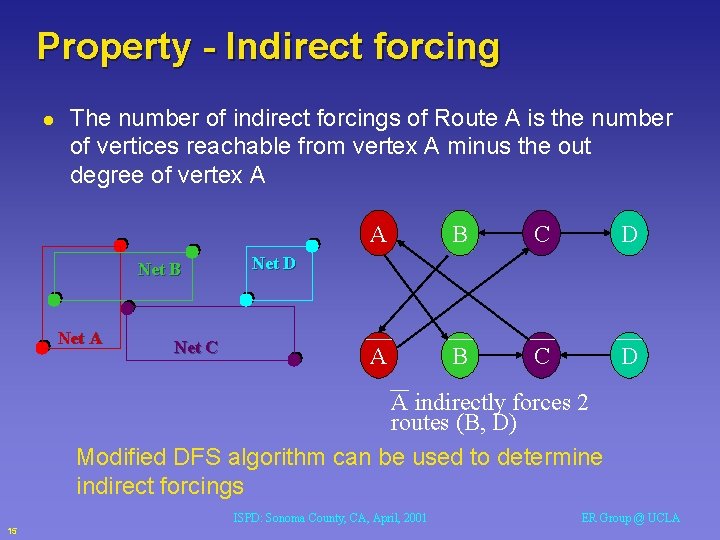
Property - Indirect forcing l The number of indirect forcings of Route A is the number of vertices reachable from vertex A minus the out degree of vertex A Net B Net A Net C A B C D Net D A indirectly forces 2 routes (B, D) Modified DFS algorithm can be used to determine indirect forcings ISPD: Sonoma County, CA, April, 2001 15 ER Group @ UCLA

MAX-CFL Definition l l Given a set of two-terminal nets S and a positive integer K < |S|. Is there a single bend routing for at least K nets such that no two routings couple? Additional routing constraints can easily be added l l Routed nets must be planar Routed nets must be routed on two layers MAX-CFL for planar layouts is NP-Complete General MAX-CFL NP-Complete? ISPD: Sonoma County, CA, April, 2001 16 ER Group @ UCLA

Algorithms l We developed three algorithms l l Greedy Direct Forcing Implication Presented at ASIC’ 00 Algorithms try to maximize number of nets routed and/or criticality of routed nets ISPD: Sonoma County, CA, April, 2001 17 ER Group @ UCLA

Implication Algorithm 1 Given a set of nets N 2 Create an implication graph G(V, E) 3 R NULL 4 for each vertex v V 5 do r. net route(v) 6 r. num_forcing Forcings(route(v)) 7 R RUr 8 Sort R by function(direct forcings, indirect forcings) 9 for each routing r R 10 do if r. net is unrouted and r is routable 11 then route r Running time is O(n 3) ISPD: Sonoma County, CA, April, 2001 18 ER Group @ UCLA

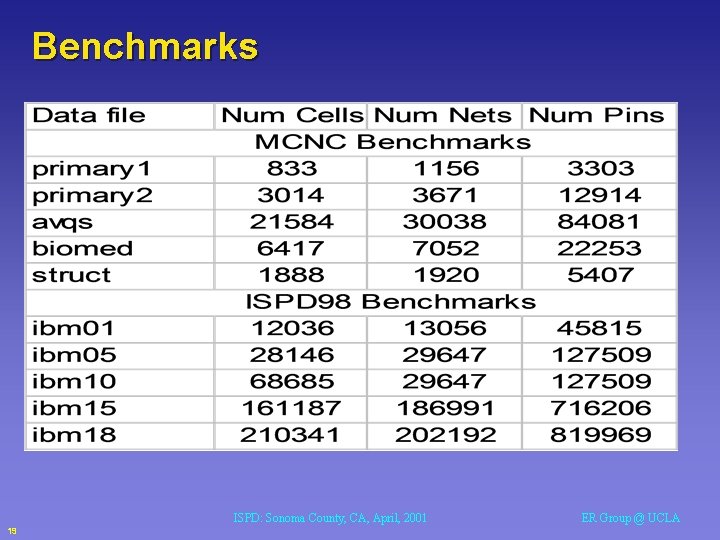
Benchmarks ISPD: Sonoma County, CA, April, 2001 19 ER Group @ UCLA

Experimental Flow Benchmark: Select {fract, biomed, x most ibm 01, etc. } critical nets greedy, direct forcing, implication algorithms Perform Statistics: MAX-CFL {criticality, % routed} algorithm x = {25, 50, 75, … , 250} Results ISPD: Sonoma County, CA, April, 2001 20 ER Group @ UCLA

Conclusion l Coupling-free routing useful for many routing algorithms l l Benefits of CFR l l l Detailed routing Global routing Single layer routing Smaller interconnect delay Aides wire planning Speeds up routing process Implication algorithm maximizes routes placed Greedy algorithm maximizes criticality placed Open problems – extending to consider weighted edges ISPD: Sonoma County, CA, April, 2001 21 ER Group @ UCLA