An Engineers Guide to MATLAB Chapter 4 AN

An Engineer’s Guide to MATLAB Chapter 4 – Objective Introduce various means of controlling the order in which a program’s expressions get evaluated and a set of relational and logical operators that are used to accomplish this control. Copyright © Edward B. Magrab 2009 2

An Engineer’s Guide to MATLAB Chapter 4 Topics • Introduction – Logical Operators • Control of Program Flow § Branching – if Statement § Branching – switch Statement § Specified repetition – for Loop § Unspecified repetition – while Loop § Early Termination of a for or while Loop Copyright © Edward B. Magrab 2009 3

An Engineer’s Guide to MATLAB Chapter 4 Program Control • Achieved by four program flow control structures – while, if, for, and switch • Each time one of these statements appears, it must be followed at a later place within the program by an end statement. • All expressions that appear between the control structure statement and the end statement are executed until all requirements of the structure are satisfied. • Each of these control structure statements can appear as often as necessary within themselves or within other control structures. When this occurs, they are called nested structures. Copyright © Edward B. Magrab 2009 4

An Engineer’s Guide to MATLAB Chapter 4 • Control structures frequently rely on relational and logical operators to determine whether a condition has been met. • When a condition has been met, the structure directs the program to a specific part of the program to execute one or more expressions. • One can use the relational and logical operators to create a logical function whose output is 1 if the relational and logical operations are true and 0 if they are false. Copyright © Edward B. Magrab 2009 5

An Engineer’s Guide to MATLAB Chapter 4 Relational and Logical Operators Copyright © Edward

An Engineer’s Guide to MATLAB Chapter 4 When using control structures – • Indent the statements following each control structure definition up to, but not including, the end statement. Greatly improves the readability. • When the structures are nested, the entire nested structure is indented, with each nested structure’s indentation preserved. • When using MATLAB's editor, the indenting can be done automatically. Copyright © Edward B. Magrab 2009 7

An Engineer’s Guide to MATLAB Chapter 4 Logical Operator – Suppose that we want to create a function g(x) such that g(x) = f(x) =0 a x<b x < a and b x The logical operator is formed by y = (a<=x & x<b) where a and b have been assigned numerical values prior to this statement and (a<=x & x<b) is the logical operator that has a value of 1 (true) when x a and x < b. Its value is 0 (false) for all other values of x. Copyright © Edward B. Magrab 2009 8

An Engineer’s Guide to MATLAB Chapter 4 If we let a = 1, b=2 f(x) = ex/2, x = [ 4, 1, 1, 4] then a script using the logical operator is a = -1; b = 2; x = [-4, -1, 1, 4]; r = (a <= x) p = (x < b) logi = (r & p) gofx = exp(x/2). *logi which, upon execution, yields Copyright © Edward B. Magrab 2009 9

An Engineer’s Guide to MATLAB Chapter 4 r= 0 1 1 1 p= 1 1 1 0 logi = 0 1 1 0 gofx = 0 0. 6065 1. 6487 0 where the intermediate expressions r, p, and logi were introduced to explicitly show that they are each a vector of logical results; ones (true) and zeros (false). Notice that dot multiplication was employed because x and logi are each (1× 4) vectors. Copyright © Edward B. Magrab 2009 10

An Engineer’s Guide to MATLAB Chapter 4 In practice, the expressions r, p, logi and gofx are combined into one expression as shown below. a = -1; b = 2; x = [-4, -1, 1, 4]; gofx = exp(x/2). *((a<=x) & (x<b)) Copyright © Edward B. Magrab 2009 11

An Engineer’s Guide to MATLAB Chapter 4 This logical operator can be used to create the unit step function u(t), which is defined as If t varies by increments of 0. 25 in the range 1 t 1, then the following script creates the unit step function t = -1: 0. 25: 1; Unit. Step = (t>=0); disp(' t Unit. Step') disp([t' Unit. Step']) Copyright © Edward B. Magrab 2009 t Unit. Step -1. 0000 0 -0. 7500 0 -0. 5000 0 -0. 2500 0 0 1. 0000 0. 2500 1. 0000 0. 5000 1. 0000 0. 7500 1. 0000 12

An Engineer’s Guide to MATLAB Chapter 4 Example – Compare two vectors of equal length. Then a = [4, 5, 6, 7, 8]; b = [4, 3, 2, 1, 8]; d = (a == b) e = (a > b) Its execution gives d= 1 e= 0 Copyright © Edward B. Magrab 2009 0 0 0 1 1 0 13

An Engineer’s Guide to MATLAB Chapter 4 Control of Program Flow if Statement The if statement is a conditional statement that branches to different parts of its structure depending on the satisfaction of certain conditional expressions. The general form of the if statement is if condition #1 expressions #1 elseif condition #2 expressions #2 else expressions #3 end Copyright © Edward B. Magrab 2009 % (optional) 14

An Engineer’s Guide to MATLAB Chapter 4 Example – if j == 1 z = sin(x) ; if nnum <= 4 nr = 1 ; nc = 1; else nr = 1 ; nc = 2; end else nr = 2; nc = 1; end Copyright © Edward B. Magrab 2009 Executed only when j = 1. This if statement encountered only when j = 1. These statements executed only when j = 1 and nnum 4. These statements executed only when j = 1 and nnum > 4. These statements executed only when j 1. 15

An Engineer’s Guide to MATLAB Chapter 4 Note: When comparing a vector to a scalar, the condition is satisfied only when each element in the vector satisfies the condition. Copyright © Edward B. Magrab 2009 16

An Engineer’s Guide to MATLAB Chapter 4 Switch Statement The switch structure is, essentially, an alternative to using a series of if-else-end structures. The general form of the switch statement is switch_expression case_expression #1 statements #1 case_expression #2 statements #2 case_expression #n statements #n otherwise statements #n+1 end Copyright © Edward B. Magrab 2009 17

An Engineer’s Guide to MATLAB Chapter 4 Example – k = 3; switch k case 1 disp('Case 1') case {2, 3} disp('Case 2 or 3' ) case 9 disp('Case 9') otherwise disp('Otherwise') end Copyright © Edward B. Magrab 2009 Executed only when k = 1 Notice that cell is used Executed only when k = 2, 3 Executed only when k = 9 Executed only when k 1, 2, 3, or 9 18

An Engineer’s Guide to MATLAB Chapter 4 for Loop A for loop repeats a series of statements a specific number of times. Its general form is for variable = expression statements end where one or more of the statements can be a function of variable. Copyright © Edward B. Magrab 2009 19

An Engineer’s Guide to MATLAB Chapter 4 Array Pre-allocation – Consider a single for loop of the form A = zeros(Nrow, 1); % Array pre-allocation for r = 1: Nrow Statements A(r) =. . . end where Nrow is a positive integer that previously has been assigned a numerical value. The addition of the array assignment statement A = zeros(Nrow, 1); ensures that the loop executes at maximum speed. Copyright © Edward B. Magrab 2009 20

An Engineer’s Guide to MATLAB Chapter 4 For nested for loops, we have that B = zeros(Nrow, Ncol); % Array pre-allocation for c = 1: Ncol % Column must be outer loop index Statements for r = 1: Nrow % Row must be inner loop index Statements B(r, c) =. . . % Index order must be as shown end where Nrow and Ncol are positive integers that previously have been assigned numerical values. Copyright © Edward B. Magrab 2009 21

An Engineer’s Guide to MATLAB Chapter 4 Example – Creation of a Sequentially-numbered Square Matrix We shall generate an (N×N) matrix in which the elements of each row are such that a 11 = 1 and a 1 n = N a 21 = N+1 and a 2 n = 2 N … a. N 1 = (N 1)N +1 and a. NN = N 2 The script is Copyright © Edward B. Magrab 2009 22

An Engineer’s Guide to MATLAB Chapter 4 N = input('Enter a positive integer < 15: '); Matr = zeros(N, N); for r = 1: N Matr(r, 1: N) = ((r-1)*N+1): r*N; end disp(Matr) Upon execution, we obtain Enter a positive integer < 15: 9 1 2 3 4 5 6 7 8 10 11 12 13 14 15 16 19 20 21 22 23 24 25 28 29 30 31 32 33 34 37 38 39 40 41 42 43 46 47 48 49 50 51 52 55 56 57 58 59 60 61 64 65 66 67 68 69 70 73 74 75 76 77 78 79 Copyright © Edward B. Magrab 2009 9 17 26 35 44 53 62 71 80 18 27 36 45 54 63 72 81 23

An Engineer’s Guide to MATLAB Chapter 4 Example – Dot Multiplication of Matrices We shall perform the dot multiplication of two matrices A and B of the same order. The script is equivalent to A. *B. In our case, we will illustrate the procedure using A = magic(3) and B = A'. However, in general, before the multiplication can be performed, one must ensure that the order of the matrices is equal. The script is Copyright © Edward B. Magrab 2009 24

An Engineer’s Guide to MATLAB Chapter 4 A = magic(3); B = A'; [r. A, c. A] = size(A); [r. B, c. B] = size(B); if (r. A~=r. B)||(c. A~=c. B) error('Matrices must be the same size') end M = zeros(r. A, c. A); for c = 1: c. A for r = 1: r. A M(r, c) = A(r, c)*B(r, c); end disp(M) Copyright © Edward B. Magrab 2009 25

An Engineer’s Guide to MATLAB Chapter 4 Upon execution, we obtain 64 3 25

An Engineer’s Guide to MATLAB Chapter 4 Example – Analysis of the Frequency Spectrum of a Three Degree-of-Freedom System Consider the following solution to a three degreeof-freedom system as a function of the forcing frequency . where We shall determine the maximum value of Yj, j = 1, 2, 3, when we take 1000 values of in the range 0 3. 5. Copyright © Edward B. Magrab 2009 27

An Engineer’s Guide to MATLAB Chapter 4 N = 1000; B = [14, 8, 2. 5]; A = [27, 14, 4; 14, 8, 2. 5; 4, 2. 5, 1]; Om 2 = linspace(0, 3. 5, N). ^2; sav = zeros(N, 3); for k = 1: N sav(k, : ) = inv(eye(3)-Om 2(k)*A)*B'; end for h = 1: 3 [mx, ix] = max(sav(: , h)); disp(['Max of Y(' int 2 str(h) ') = ' num 2 str(mx, 6) ' at Omega = ' num 2 str(sqrt(Om 2(ix)), 4)]) end Copyright © Edward B. Magrab 2009 28

An Engineer’s Guide to MATLAB Chapter 4 Upon execution, we obtain Max of Y(1) = 1731. 45 at Omega = 0. 1682 Max of Y(2) = 921. 09 at Omega = 0. 1682 Max of Y(3) = 532. 522 at Omega = 2. 971 Copyright © Edward B. Magrab 2009 29

An Engineer’s Guide to MATLAB Chapter 4 Example - Total Interest of a Loan Compute the total interest on a loan when the amount of the loan is L, its duration is m months, and its annual percentage interest Ia. The monthly payment pmon is determined from where i = Ia/1200 is the monthly interest rate expressed as a decimal number. As the loan is being paid off, a portion of the payment is used to pay the interest, and the remainder is applied to the unpaid loan amount. The unpaid loan amount after each payment is called the balance. Copyright © Edward B. Magrab 2009 30

An Engineer’s Guide to MATLAB Chapter 4 If b 0 = L, then where in is the portion of pmon that goes towards the payment of the interest. Pn is the portion of the payment that goes towards the reduction of the balance bn—that is, the amount required to pay off the loan. The total interest paid at the end of the loan’s duration is Copyright © Edward B. Magrab 2009 31

An Engineer’s Guide to MATLAB Chapter 4 The script to compute i. T is loan = input('Enter loan amount: '); durat = input('Enter term of loan in months: '); int = input('Enter annual interest rate: ')/1200; ints = zeros(durat, 1); % Pre-allocation prins = ints; % Pre-allocation bals = ints; % Pre-allocation pmon = (loan*int)/(1 -(1+int)^(-durat)); bals(1) = loan; for m = 2: durat+1 ints(m) = int*bals(m-1); prins(m) = pmon-ints(m); bals(m) = bals(m-1)-prins(m); end disp(['Total interest = ', num 2 str(sum(ints), 8)]) Copyright © Edward B. Magrab 2009 32

An Engineer’s Guide to MATLAB Chapter 4 Execution of the script gives Enter loan amount: 100000 Enter term of loan in months: 360 Enter annual interest rate: 8 Total interest = $164155. 25 The first three lines were answered by the user, the last line is the result. Copyright © Edward B. Magrab 2009 33

An Engineer’s Guide to MATLAB Chapter 4 Example - Specification of the Elements of an Array We shall create an (n×n) matrix whose elements are either +1 or 1 such that The script is Copyright © Edward B. Magrab 2009 34

An Engineer’s Guide to MATLAB Chapter 4 n = input('Enter the order of the square matrix: '); k = 1: n; M = zeros(n, n); Odd. Row = (-1). ^(k-1); Even. Row = (-1). ^k; for m = 1: 2: n M(m, : ) = Odd. Row; if m+1 <= n M(m+1, : ) = Even. Row; end disp(M) Copyright © Edward B. Magrab 2009 35

An Engineer’s Guide to MATLAB Chapter 4 The execution of this script for n = 3 displays to the command window Enter the order of the square matrix: 3 1 -1 1 where the value 3 was entered by the user. Copyright © Edward B. Magrab 2009 36

An Engineer’s Guide to MATLAB Chapter 4 Example - Sorting a Vector of Numerical Values in Ascending Order We shall create a script that does the same thing sort. H = [17, 12, -6, 0, -14]; LH = length(H); for k = 1: (LH-1) smin = H(k); for m = (k+1): LH if H(m) < smin = H(m); M = m; end temp = H(k); H(k) = H(M); H(M) = temp; end disp(H) Copyright © Edward B. Magrab 2009 The execution of the script gives -14 -6 0 12 12 17 37

An Engineer’s Guide to MATLAB Chapter 4 while Loop The while loop repeats one or more statements an indefinite number of times, leaving the loop only when a specified condition has been satisfied. Its general form is while condition statements end where the expression defining condition is usually composed of one or more of the variables evaluated by statements. Copyright © Edward B. Magrab 2009 38

An Engineer’s Guide to MATLAB Chapter 4 Example - Approximation to The following expression converges to 1/ when and yo = 1/2 where We shall show that the difference |1/ y 4| is less than 10 15. The script is Copyright © Edward B. Magrab 2009 39

An Engineer’s Guide to MATLAB Chapter 4 xo = 1/sqrt(2); yo = 1/2; n = 0; while abs(1/pi - yo) > 1 e-15 xo = (1 -sqrt(1 -xo^2))/(1+sqrt(1 -xo^2)); yo = yo*(1+xo)^2 -2^(n+1)*xo; n = n+1; end fprintf(1, 'For n = %2. f, |1/pi-y_(n+1)| = %5. 4 en', n-1, abs(1/pi - yo)) Execution of this script results in For n = 3, |1/pi-y_(n+1)| = 4. 9960 e-016 Copyright © Edward B. Magrab 2009 40

An Engineer’s Guide to MATLAB Chapter 4 Example – Interval Halving and the Roots of Functions Find a series of positive values of x (x 1, x 2, …) that make f(x) = 0, assuming that the sign of f(x) alternates as x increases Copyright © Edward B. Magrab 2009 41

An Engineer’s Guide to MATLAB Chapter 4 n = 5; a = pi; increment = 0. 3; tolerance = 1 e-6; xstart = 0. 2; x = xstart; dx = increment; for m = 1: n s 1 = sign(cos(a*x)); f(x) = cos(ax) 0 while dx/x > tolerance if s 1 ~= sign(cos(a*(x+dx))) dx = dx/2; else x = x+dx; end route(m) = x; dx = increment; x = 1. 05*x; end 0. 5000 1. 5000 2. 5000 3. 5000 4. 5000 disp(route) Copyright © Edward B. Magrab 2009 42

An Engineer’s Guide to MATLAB Chapter 4 Example – Convergence of a Series Determine and display the number of terms that it takes for the series to converge to within 0. 01% of its exact value, which is S = 2/6. Copyright © Edward B. Magrab 2009 43

An Engineer’s Guide to MATLAB Chapter 4 series = 1; k = 2; exact = pi^2/6; while abs((series-exact)/exact) >= 1 e-4 series = series+1/k^2; k = k+1; end disp(['Number of terms = ' num 2 str(k-1)]) which, upon execution, displays to the command window Number of terms = 6079 Copyright © Edward B. Magrab 2009 44

An Engineer’s Guide to MATLAB Chapter 4 Early Termination of Either a for or while Loop The break function is used to terminate either a for or while loop. If the break function is within nested for or while loops, then it returns to the next higher level for or while loop. Copyright © Edward B. Magrab 2009 45

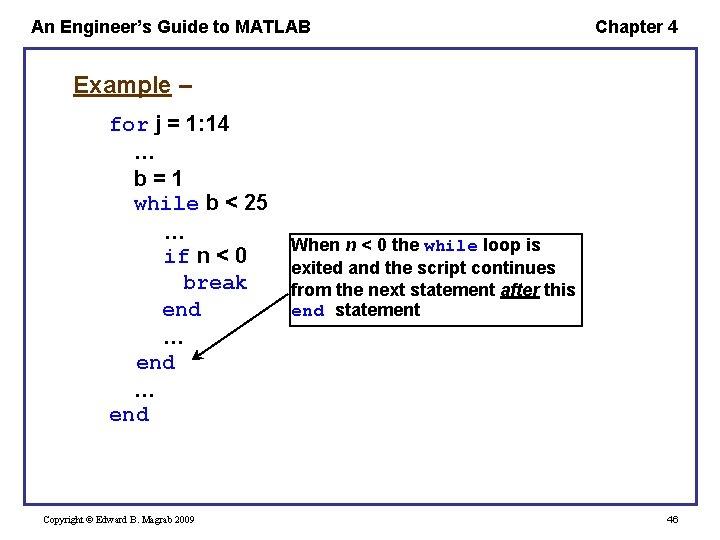
An Engineer’s Guide to MATLAB Chapter 4 Example – for j = 1: 14 … b=1 while b < 25 … if n < 0 break end … end Copyright © Edward B. Magrab 2009 When n < 0 the while loop is exited and the script continues from the next statement after this end statement 46