An Engineers Guide to MATLAB Chapter 2 AN

An Engineer’s Guide to MATLAB Chapter 2 – Objective Introduce MATLAB syntax in the

An Engineer’s Guide to MATLAB Chapter 2 Topics • Definitions of Matrices and Vectors • Creation of Matrices • Dot Operations • Mathematical Operations with Matrices § Addition and Subtraction § Multiplication § Determinants § Matrix Inverse § Solution of a System of Equations Copyright © Edward B. Magrab 2009 3

An Engineer’s Guide to MATLAB Chapter 2 Definitions of Matrices and Vectors An array A of m rows and n columns is called a matrix of order (m n) and is written as The elements of the matrix are denoted aij, where i indicates the row number and j the column number. Square Matrix: n = m Copyright © Edward B. Magrab 2009 4

An Engineer’s Guide to MATLAB Chapter 2 Diagonal Matrix: When n = m and

An Engineer’s Guide to MATLAB Chapter 2 Column Matrix - Vector: When aij = ai 1 (there is only one column), then Row Matrix - Vector: When aij = a 1 j, (there is only one row), then Default definition of a vector in MATLAB Copyright © Edward B. Magrab 2009 6

An Engineer’s Guide to MATLAB Chapter 2 Transpose of a Matrix and a Vector The transpose of a matrix is denoted by an apostrophe ( ). If A is defined as before and W = A , then Recall that Copyright © Edward B. Magrab 2009 7

An Engineer’s Guide to MATLAB Chapter 2 For a column vector - For a

An Engineer’s Guide to MATLAB Chapter 2 Creation of Vectors If a, x, b, … are either variable names, numbers, expressions, or strings, then vectors are expressed as either f = [a x b …] (Blanks required) or f = [a, x, b, …] (Blanks optional) Caution about blanks: If a = h + ds, then f is written as either f = [h+d^s x b. . . ] No blanks permitted or within expression f = [h+d^s, x, b, . . . ] Copyright © Edward B. Magrab 2009 9

An Engineer’s Guide to MATLAB Chapter 2 Ways to Assign Numerical Values to the Elements of a Vector • Specify the range of the values and the increment between adjacent values – called colon notation. Used when the increment is either important or has been specified. • Specify the range of the values and the number of values desired. Used when the number of values is important. Copyright © Edward B. Magrab 2009 10

An Engineer’s Guide to MATLAB Chapter 2 If s, d, and f are any combination of numerical values, variable names, and expressions, then the colon notation that creates a vector x is either x = s: d: f or x = (s: d: f) or x = [s: d: f] where s = start or initial value d = increment or decrement f = end or final value Thus, the following row vector x is created x = [s, s+d, s+2 d, …, s+nd] (Note: s+nd f ) Copyright © Edward B. Magrab 2009 11

An Engineer’s Guide to MATLAB Chapter 2 Also, when d is omitted MATLAB assumes that d = 1. Then x = s: f creates the vector x = [s, s+1, s+2, … , s+n] where s+n f The number of terms, called the length of the vector, that this expression has created is determined from length(x) Copyright © Edward B. Magrab 2009 12

An Engineer’s Guide to MATLAB Chapter 2 Example – Create a row vector that goes from 0. 2 to 1. 0 in increments of 0. 1. x = 0. 2: 0. 1: 1 n = length(x) When executed, we obtain x= 0. 20 0. 30 0. 40 0. 50 0. 60 0. 70 0. 80 0. 90 1. 00 x= n= 0. 2000 9 0. 3000 0. 4000 To create a column vector, we use 0. 5000 0. 6000 x = (0. 2: 0. 1: 1) 0. 7000 0. 8000 n = length(x) 0. 9000 1. 0000 n= 9 Copyright © Edward B. Magrab 2009 13

An Engineer’s Guide to MATLAB Chapter 2 Generation of n Equally Spaced Values x = linspace(s, f, n) where the increment (decrement) is computed by MATLAB from The values of s and f can be either positive or negative and either s > f or s < f. When n is not specified, it is assigned a value of 100. Thus, linspace creates the vector x = [s, s+d, s+2 d, …, f = s+(n 1)d] Copyright © Edward B. Magrab 2009 14

An Engineer’s Guide to MATLAB Chapter 2 If equal spacing on a logarithmic scale is desired, then x = logspace(s, f, n) where the initial value is xstart = 10 s, the final value is xfinal = 10 f and d is defined above. This expression creates the row vector x = [10 s 10 s+d 10 s+2 d … 10 f] Copyright © Edward B. Magrab 2009 15

An Engineer’s Guide to MATLAB Chapter 2 Examples x = linspace(0, 2, 5) gives x= 0 0. 5000 1. 0000 1. 5000 2. 0000 and x = logspace(0, 2, 5) % [100, 100. 5, 101. 5, 102] gives x= 1. 0000 3. 1623 10. 0000 31. 6228 100. 0000 Copyright © Edward B. Magrab 2009 16

An Engineer’s Guide to MATLAB Chapter 2 Transpose of a Vector with Complex Values If a vector has elements that are complex numbers, then taking its transpose also converts the complex quantities to their complex conjugate values. Consider the following script z = [1, 7+4 j, -15. 6, 3. 5 -0. 12 j]; w = z which, upon execution, gives w= 1. 0000 7. 0000 - 4. 0000 i -15. 6000 3. 5000 + 0. 1200 i Copyright © Edward B. Magrab 2009 17

An Engineer’s Guide to MATLAB Chapter 2 If the transpose is desired, but not the conjugate, then the script is written as z = [1, 7+4 j, -15. 6, 3. 5 -0. 12 j]; w = conj(z') which, upon execution, gives w= 1. 0000 7. 0000 + 4. 0000 i -15. 6000 3. 5000 - 0. 1200 i Copyright © Edward B. Magrab 2009 18

An Engineer’s Guide to MATLAB Chapter 2 Accessing Elements of Vectors – Subscript Notation Consider the row vector b = [b 1 b 2 b 3 … bn] Access to one or more elements of this vector is accomplished using subscript notation in which the subscript refers to the location in the vector as follows: b(1) b 1 … b(k) bk. . . b(n) bn Copyright © Edward B. Magrab 2009 % or b(end) 19

An Engineer’s Guide to MATLAB Chapter 2 Example – x = [-2, 1, 3,

An Engineer’s Guide to MATLAB Chapter 2 Accessing Elements of Vectors Using Subscript Colon Notation The subscript colon notation is a shorthand method of accessing a group of elements. For a vector b with n elements, one can access a group of them using the notation b(k: d: m) where 1 k < m n, k and m are positive integers and, in this case, d is a positive integer. Thus, if one has 10 elements in a vector b, the third through seventh elements are selected by using b(3: 7) Copyright © Edward B. Magrab 2009 21

An Engineer’s Guide to MATLAB Chapter 2 Example – Consider the following script z = [-2, 1, 3, 5, 7, 9, 10]; z(2) = z(2)/2; z(3: 4) = z(3: 4)*3 -1; z When executed, we obtain z= -2. 00 0. 50 8. 00 14. 00 7. 00 9. 00 10. 00 Copyright © Edward B. Magrab 2009 22

An Engineer’s Guide to MATLAB Chapter 2 Example – Consider the script y = [-1, 6, 15, -7, 31, 2, -4, -5]; x = y(3: 5) whose execution creates the three-element vector x= 15 Copyright © Edward B. Magrab 2009 -7 31 23

An Engineer’s Guide to MATLAB Chapter 2 Example – We shall show that there are several ways to create a vector x that is composed of the first two and the last two elements of a vector y. Thus, y = [-1, 6, 15, -7, 31, 2, -4, -5]; x = [y(1), y(2), y(7), y(8)] or y = [-1, 6, 15, -7, 31, 2, -4, -5]; index = [1, 2, 7, 8]; % or [1: 2, length(y)-1, length(y)] x = y(index) or more compactly y = [-1, 6, 15, -7, 31, 2, -4, -5]; x = y([1, 2, 7, 8]) % or y([1: 2, length(y)-1, length(y)]) Copyright © Edward B. Magrab 2009 24

An Engineer’s Guide to MATLAB Chapter 2 Two useful functions: sort and find sort: Sorts a vector y in ascending order (most negative to most positive) or descending order (most positive to most negative) [ynew, indx] = sort(y, mode) % mode = 'ascend‘ or 'descend' where ynew is the vector with the rearranged (sorted) elements of y and indx is a vector containing the original locations of the elements in y. find: Determines the locations (not the values) of all the elements in a vector (or matrix) that satisfy a user-specified relational and/or logical condition or expression Expr indxx = find(Expr) Copyright © Edward B. Magrab 2009 25

An Engineer’s Guide to MATLAB Chapter 2 Example – y = [-1, 6, 15, -7, 31, 2, -4, -5]; z = [10, 20, 30, 40, 50, 60, 70, 80]; [ynew, indx] = sort(y, 'ascend') znew = z(indx) when executed, gives ynew = -7 -5 -4 -1 2 6 15 31 indx = 4 8 7 1 6 2 3 5 znew = 40 80 70 10 60 20 30 50 Copyright © Edward B. Magrab 2009 26

An Engineer’s Guide to MATLAB Chapter 2 Example – y = [-1, 6, 15, -7, 31, 2, -4, -5]; indxx = find(y<=0) s = y(indxx) Upon execution, we obtain indxx = 1 4 7 8 s= -1 -7 -4 -5 Copyright © Edward B. Magrab 2009 27

An Engineer’s Guide to MATLAB Chapter 2 One of the great advantages of MATLAB’s implicit vector and matrix notation is that it provides the user with a compact way of performing a series of operations on an array of values. Example – The script x = linspace(-pi, 10); y = sin(x) yields the following vector y= -0. 0000 -0. 6428 -0. 9848 -0. 8660 -0. 3420 0. 8660 0. 9848 0. 6428 0. 0000 Copyright © Edward B. Magrab 2009 0. 3420 28

An Engineer’s Guide to MATLAB Chapter 2 Minimum and Maximum Values of a Vector: min and max To find the magnitude of the smallest element xmin and its location locmin in a vector, we use [xmin, locmin] = min(x) To find the magnitude of the largest element xmax and its location locmax in a vector, we use [xmax, locmax] = max(x) Copyright © Edward B. Magrab 2009 29

An Engineer’s Guide to MATLAB Chapter 2 Example – x = linspace(-pi, 10); y = sin(x); [ymax, kmax] = max(y) [ymin, kmin] = min(y) Upon execution, we find that ymax = 0. 9848 kmax = y= 8 -0. 0000 -0. 6428 -0. 9848 -0. 8660 -0. 3420 ymin = 0. 3420 0. 8660 0. 9848 0. 6428 0. 0000 -0. 9848 kmin = 3 Copyright © Edward B. Magrab 2009 30

An Engineer’s Guide to MATLAB Chapter 2 Example - Analysis of the elements of a vector Consider 50 equally-spaced points of the following function We shall (a) determine the time at which the minimum positive value of f(t) occurs (b) the average value of its negative values The script is Copyright © Edward B. Magrab 2009 31

An Engineer’s Guide to MATLAB Chapter 2 t = linspace(0, 2*pi, 50); f = sin(t); f. Avg. Neg = mean(f(find(f<0))) Min. Valuef = min(f(find(f>0))); t. Min. Valuef = t(find(f==Min. Valuef)) Upon execution, we find that f. Avg. Neg = -0. 6237 t. Min. Valuef = 3. 0775 Copyright © Edward B. Magrab 2009 32

An Engineer’s Guide to MATLAB Chapter 2 Creation of Matrices The basic syntax to create a matrix is A = [a 11 a 12 a 13; a 21 a 22 a 23; a 31 a 32 a 33; a 41 a 42 a 43] where the semicolons are used to indicate the end of a row and the aij can be numbers, variable names, expressions, or strings. Alternate ways are: A = [a 11 a 12 a 21 a 22 a 31 a 32 a 41 a 42 a 13; . . . a 23; . . . a 33; . . . a 43] where the ellipses (. . . ) are required to indicate that the expression continues on the next line. Copyright © Edward B. Magrab 2009 33

An Engineer’s Guide to MATLAB Chapter 2 For the second alternate way, One can omit the ellipsis (…) and instead to use the Enter key to indicate the end of a row. In this case, the expression will look like A = [a 11 a 12 a 21 a 22 a 31 a 32 a 41 a 42 Copyright © Edward B. Magrab 2009 a 13 %<Enter> a 23 %<Enter> a 33 %<Enter> a 43] 34

An Engineer’s Guide to MATLAB Chapter 2 For a third alternate way, Create four separate row vectors, each with the same number of columns, and then combine these vectors to form the matrix as follows v 1 = [ a 11 a 12 a 13]; v 2 = [ a 21 a 22 a 23]; v 3 = [ a 31 a 32 a 33]; v 4 = [ a 41 a 42 a 43]; A = [ v 1; v 2; v 3; v 4] where the semicolons in the first four lines are used to suppress display to the command window. The order of the matrix is determined by [r, c] = size(A) Copyright © Edward B. Magrab 2009 35

An Engineer’s Guide to MATLAB Chapter 2 Transpose of a matrix with complex elements If a matrix has elements that are complex numbers, then taking its transpose also converts the complex quantities to their complex conjugate values. Consider the following script Z = [1+2 j, 3+4 j; 5+6 j, 7+9 j] W = Z' the execution of which gives Z= 1. 0000 + 2. 0000 i 5. 0000 + 6. 0000 i W= 1. 0000 - 2. 0000 i 3. 0000 - 4. 0000 i Copyright © Edward B. Magrab 2009 3. 0000 + 4. 0000 i 7. 0000 + 9. 0000 i 5. 0000 - 6. 0000 i 7. 0000 - 9. 0000 i 36

An Engineer’s Guide to MATLAB Chapter 2 Special Matrices A matrix of all 1’s ones(r, c) on(1: r, 1: c) = 1 on = ones(2, 5) on = 1 1 1 1 1 A null matrix zeros(r, c) zer(1: r, 1: c) = 0 Copyright © Edward B. Magrab 2009 zer = zeros(3, 2) zer = 0 0 0 37

An Engineer’s Guide to MATLAB Chapter 2 Diagonal matrix – Create an (n n) diagonal matrix whose diagonal elements are a vector a of length n diag(a) a = [4, 9, 1]; A = diag(a) A= 4 0 0 0 9 0 0 0 1 Extract the diagonal elements of a square matrix A Ad = diag([11, 12, 13, 14; … 21, 22, 23, 24; … 31, 32, 33, 34; … 41, 42, 43, 44]) diag(A) Ad = 11 22 33 44 Copyright © Edward B. Magrab 2009 38

An Engineer’s Guide to MATLAB Chapter 2 Identity matrix whose size is (n n)

An Engineer’s Guide to MATLAB Accessing Matrix Elements Chapter 2 Matrix created with – A = [3: 2: 11; … linspace(20, 21, 5); … ones(1, 5)]; : means all elements of row 2 : means all elements of column 2 Copyright © Edward B. Magrab 2009 B = A(1: 3, 3: 5) B= 7. 0000 9. 0000 11. 0000 20. 5000 20. 7500 21. 0000 40

An Engineer’s Guide to MATLAB Chapter 2 In several of the following examples, we shall use magic(n) which creates an (n n) matrix in which the sum of the elements in each column and the sum of the elements of each row and the sum of the elements in each diagonal are equal. For example, magic(4) creates 16 5 9 4 2 11 7 14 3 13 10 8 6 12 15 1 Copyright © Edward B. Magrab 2009 41

An Engineer’s Guide to MATLAB Chapter 2 Example – We shall set all the diagonal elements of magic(4) to zero; thus diag(Z) = diag(Z)) = Z = magic(4); 16 16 0 0 0 Z = Z-diag(Z)) 11 0 0 6 0 which results in 1 0 0 0 1 Z= 0 2 3 13 5 0 10 8 magic(4) = 9 7 0 12 16 2 3 13 4 14 15 0 5 11 10 8 9 7 6 12 4 14 15 1 Copyright © Edward B. Magrab 2009 42

An Engineer’s Guide to MATLAB Chapter 2 Example – We shall replace all the diagonal elements of magic(4) with the value 5; thus, Z = magic(4); Z = Z-diag(Z))+5*eye(4) which results in Z= 5 5 9 4 Copyright © Edward B. Magrab 2009 2 3 13 5 10 8 7 5 12 14 15 5 magic(4) = 16 2 3 5 11 10 9 7 6 4 14 15 13 8 12 1 43

An Engineer’s Guide to MATLAB Chapter 2 Use of find with Matrices For a matrix, [row, col] = find(Expr) where row and col are column vectors of the locations in the matrix that satisfied the condition represented by Expr. Let us find all the elements of magic(3) that are greater than 5. The script is m = magic(3) [r, c] = find(m > 5); subscr = [r c] % Column augmentation Copyright © Edward B. Magrab 2009 44

An Engineer’s Guide to MATLAB Chapter 2 Upon execution, we obtain m= 8 1

An Engineer’s Guide to MATLAB Example – Chapter 2 Minimum and Maximum Values in a Matrix M = magic(4) min. M = min(M) max. M = max(M) min and max operate on a column by column basis. which, upon execution, gives M= 16 2 5 11 9 7 4 14 min. M = 4 2 max. M = 16 14 Copyright © Edward B. Magrab 2009 3 13 10 8 6 12 15 1 To find the maximum of all elements we use max twice: 3 which, upon execution, gives 15 1 13 M = magic(4); max. M = max(M)) max. M = 16 46

An Engineer’s Guide to MATLAB Chapter 2 Example - Creation of a special matrix We shall create the following (9× 9) array (Dashed lines have been added to enhance visual clarity. ) Copyright © Edward B. Magrab 2009 47

An Engineer’s Guide to MATLAB Chapter 2 The script is a = ones(3, 3)-eye(3); A = [a, 2*a, 3*a; 4*a, 5*a, 6*a; 7*a, 8*a, 9*a; ] Upon execution, we obtain A= 0 1 1 0 4 4 0 7 7 1 0 1 4 0 4 7 0 7 Copyright © Edward B. Magrab 2009 1 1 0 4 4 0 7 7 0 0 2 2 0 5 5 0 8 8 2 0 2 5 0 5 8 0 8 2 2 0 5 5 0 8 8 0 0 3 3 0 6 6 0 9 9 3 0 3 6 0 6 9 0 9 3 3 0 6 6 0 9 9 0 48

An Engineer’s Guide to MATLAB Chapter 2 Example - Rearrangement of Sub Matrices of a Matrix Consider the following (9× 9) array 1 4 2 3 (Dashed lines have been added to enhance visual clarity. ) Copyright © Edward B. Magrab 2009 49

An Engineer’s Guide to MATLAB Chapter 2 For the four (3 3) sub matrices identified by the circled numbers 1 to 4, we shall perform a series of swaps of these sub matrices to produce the following array 3 4 1 2 1 4 Copyright © Edward B. Magrab 2009 2 3 50

An Engineer’s Guide to MATLAB Chapter 2 The script is Matr = [1: 9; 10: 18; 19: 27; 28: 36; 37: 45; . . . 46: 54; 55: 63; 64: 72; 73: 81]; Temp 1 = Matr(1: 3, 1: 3); Matr(1: 3, 1: 3) = Matr(7: 9, 7: 9); Matr(7: 9, 7: 9) = Temp 1; Temp 1 = Matr(1: 3, 7: 9); Matr(1: 3, 7: 9) = Matr(7: 9, 1: 3); Matr(7: 9, 1: 3) = Temp 1; Matr Copyright © Edward B. Magrab 2009 51

An Engineer’s Guide to MATLAB Chapter 2 Upon execution, we obtain Matr = 61 70 79 28 37 46 7 16 25 62 71 80 29 38 47 8 17 26 63 72 81 30 39 48 9 18 27 4 13 22 31 40 49 58 67 76 5 14 23 32 41 50 59 68 77 6 15 24 33 42 51 60 69 78 55 64 73 34 43 52 1 10 19 56 65 74 35 44 53 2 11 20 57 66 75 36 45 54 3 12 21 1 4 Copyright © Edward B. Magrab 2009 2 3 52

An Engineer’s Guide to MATLAB Chapter 2 Manipulation of Arrays Two functions that create matrices by replicating a specified number of times either a scalar, a column or row vector, or a matrix are repmat and meshgrid which uses repmat. The general form of repmat is repmat(x, r, c) where x is either a scalar, vector, or matrix, r is the total number of rows of x that will be replicated, and c is the total number of columns of x will be replicated. Copyright © Edward B. Magrab 2009 53

An Engineer’s Guide to MATLAB Chapter 2 Example – We shall produce the following matrix three ways W= 45. 7200 45. 7200 Thus, W = repmat(45. 72, 3, 3) % Function or W = [45. 72, 45. 72; … % Hard code 45. 72, 45. 72; … 45. 72, 45. 72] or W(1: 3, 1: 3) = 45. 72 % Subscript colon notation Copyright © Edward B. Magrab 2009 54

An Engineer’s Guide to MATLAB Chapter 2 Example – Consider the vector s = [a 1 a 2 a 3 a 4] The expression V = repmat(s, 3, 1) creates the numerical equivalent of the matrix Replicated row Copyright © Edward B. Magrab 2009 55

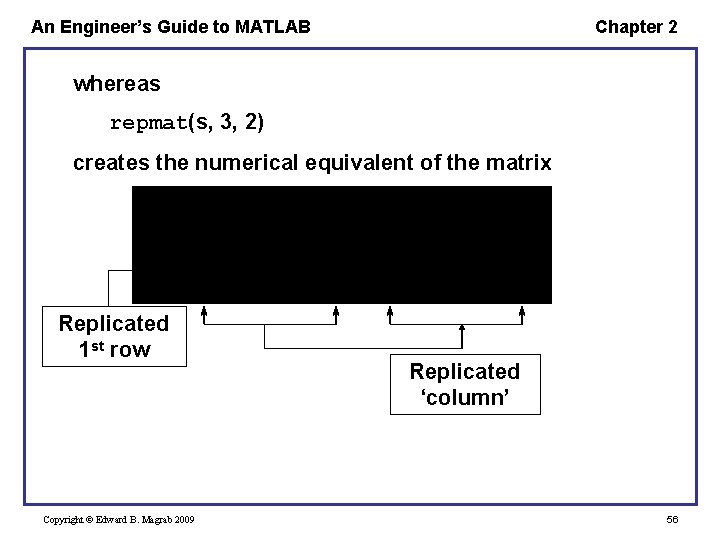
An Engineer’s Guide to MATLAB Chapter 2 whereas repmat(s, 3, 2) creates the numerical

An Engineer’s Guide to MATLAB Chapter 2 On the other hand V = repmat(s',

An Engineer’s Guide to MATLAB Chapter 2 and V = repmat(s', 2, 3) gives

An Engineer’s Guide to MATLAB Chapter 2 meshgrid If we have two row vectors s and t, then [U, V] = meshgrid(s, t) gives the same result as that produced by the two commands U = repmat(s, length(t), 1) V = repmat(t', 1, length(s)) % Notice transpose In either case, U and V are each matrices of order (length(t) length(s)) Copyright © Edward B. Magrab 2009 59

An Engineer’s Guide to MATLAB Chapter 2 Example – If s = [s 1 s 2 s 3 s 4] % (1× 4) t = [t 1 t 2 t 3] % (1× 3) then [U, V] = meshgrid(s, t) % Sizes of U and V are (3× 4) produces the numerical equivalent of two (3 4) matrices Copyright © Edward B. Magrab 2009 60

An Engineer’s Guide to MATLAB Example – u = [1, 2, 3, 4]; v = [5, 6, 7]; [U, V] = meshgrid(u, v) Upon execution, we obtain U= 1 1 1 V= 5 6 7 2 2 2 3 3 3 4 4 4 5 6 7 Copyright © Edward B. Magrab 2009 Chapter 2 However, u = [1, 2, 3, 4]; v = [5, 6, 7]; [V, U] = meshgrid(v, u) gives V= 5 5 U= 1 2 3 4 6 6 7 7 1 2 3 4 61

An Engineer’s Guide to MATLAB Chapter 2 There are two matrix manipulation functions that are useful in certain applications – fliplr(A) which flips the columns and flipud(A) which flips the rows. Consider the (2 5) matrix which is created with the statement A = [a 11 a 12 a 13 a 14 a 15; a 21 a 22 a 23 a 24 a 25] Copyright © Edward B. Magrab 2009 62

An Engineer’s Guide to MATLAB Chapter 2 Then and These results are obtained with the colon notation. For example, C = fliplr(A) produces the same results as C = A(: , length(A): -1: 1) Copyright © Edward B. Magrab 2009 63

An Engineer’s Guide to MATLAB Chapter 2 Clarification of Notation – Consider the following

An Engineer’s Guide to MATLAB Chapter 2 Column augmentation: C = [A, B] Row

An Engineer’s Guide to MATLAB Chapter 2 Furthermore, if x = [x 1 x 2 x 3] y = [y 1 y 2 y 3] then either Z = [x', y'] or Z = [x; y]' gives whereas Z = [x'; y'] yields Copyright © Edward B. Magrab 2009 66

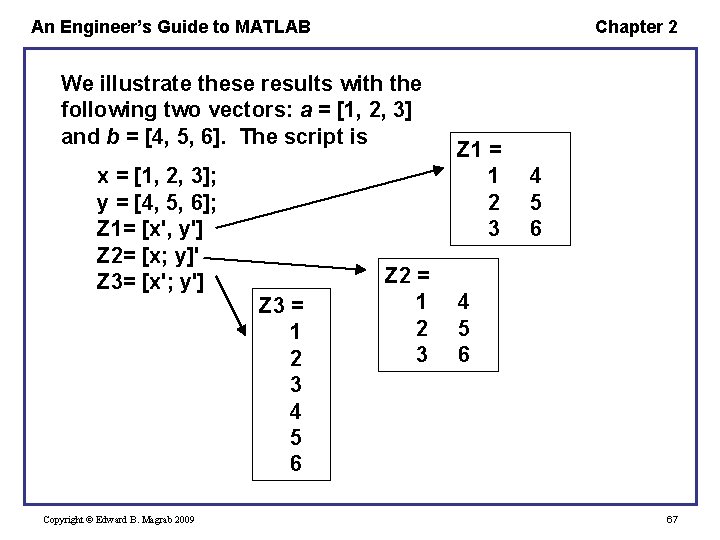
An Engineer’s Guide to MATLAB Chapter 2 We illustrate these results with the following two vectors: a = [1, 2, 3] and b = [4, 5, 6]. The script is x = [1, 2, 3]; y = [4, 5, 6]; Z 1= [x', y'] Z 2= [x; y]' Z 3= [x'; y'] Copyright © Edward B. Magrab 2009 Z 3 = 1 2 3 4 5 6 Z 2 = 1 2 3 Z 1 = 1 2 3 4 5 6 67

An Engineer’s Guide to MATLAB Chapter 2 Dot Operations A means of performing, on matrices of the same order, arithmetic operations on an element-by-element basis. Consider the following (3 4) matrices Copyright © Edward B. Magrab 2009 68

An Engineer’s Guide to MATLAB Chapter 2 Then, the dot multiplication of X and

An Engineer’s Guide to MATLAB Chapter 2 The dot exponentiation of X and M

An Engineer’s Guide to MATLAB Chapter 2 Use of Dot Operations Let a, b, c, d, and g each be a (3 2) matrix, and consider the expression Then the MATLAB expression is Z = (tan(a)-g. *(b. /c). ^d). ^2; which is equivalent to Copyright © Edward B. Magrab 2009 71

An Engineer’s Guide to MATLAB Chapter 2 Example – Evaluate for 6 equally-spaced values of t in the interval 0 t 1 when a 1 = 0. 2, b 1 = 0. 9, and c 1 = /6. The script is a 1 = 0. 2; b 1 = 0. 9; c 1 = pi/6; t = linspace(0, 1, 6); v = exp(-a 1*t). *sin(b 1*t+c 1). /(t+c 1) Upon execution, we obtain v= 0. 9549 Copyright © Edward B. Magrab 2009 0. 8590 0. 7726 0. 6900 0. 6097 0. 5316 72

An Engineer’s Guide to MATLAB Chapter 2 Example – Create the elements of an (N×N) matrix H when each element is given by The script to generate this array for N = 4 is N = 4; mm = 1: N; nn = mm; [n, m] = meshgrid(nn, mm) h = 1. /(m+n-1) Upon execution, we get Copyright © Edward B. Magrab 2009 h= 1. 0000 0. 5000 0. 3333 0. 2500 0. 2000 0. 1667 0. 1429 73

An Engineer’s Guide to MATLAB Chapter 2 We return to meshgrid and again consider the two vectors s = [s 1 s 2 s 3 s 4] and t = [t 1 t 2 t 3]. Using the MATLAB expression [U, V] = meshgrid(s, t) % U and V are (3× 4) matrices we obtained the matrices and If we perform the dot multiplication Z = U. *V then the execution of the program Copyright © Edward B. Magrab 2009 74

An Engineer’s Guide to MATLAB Chapter 2 s= [s 1, s 2, s 3, s 4]; t = [t 1, t 2, t 3]; [U, V] = meshgrid(s, t) % (3× 4) matrices Z = U. *V results in the equivalent matrix Thus, we have the product of all combinations of the elements of vectors s and t. Copyright © Edward B. Magrab 2009 75

An Engineer’s Guide to MATLAB Chapter 2 Summation and Cumulative Summation Functions sum: When v = [v 1, v 2, …, vn], then where S a scalar. If Z is a (3 4) matrix with elements zij, then To sum all the elements in an array, we use Copyright © Edward B. Magrab 2009 76

An Engineer’s Guide to MATLAB Chapter 2 Example – Evaluate Thus, m = 1:

An Engineer’s Guide to MATLAB Chapter 2 cumsum: For a vector v composed of n elements vj, cumsum creates another vector of length n whose elements are If W is (m n) matrix composed of elements wjk, then Copyright © Edward B. Magrab 2009 78

An Engineer’s Guide to MATLAB Chapter 2 Example – Consider the convergence of the series Thus, S = cumsum(1. /(1: 10). ^2) which, upon execution, gives S= 1. 0000 1. 2500 1. 3611 1. 4236 1. 4636 1. 4914 1. 5118 1. 5274 1. 5398 1. 5498 Copyright © Edward B. Magrab 2009 79

An Engineer’s Guide to MATLAB Chapter 2 Example – We shall evaluate the following series expression for the hyperbolic secant for N = 305 and for five equally spaced values of x from 0 x 2 and compare the results to the exact values. Thus, nn = 1: 2: 305; xx = linspace(0, 2, 5); [x, n] = meshgrid(xx, nn); s = 4*pi*sum(n. *(-1). ^((n-1)/2). /… ((pi*n). ^2+4*x. ^2)); se = sech(xx); compare = [xx ' s' se' (100*(s-se). /se)'] Copyright © Edward B. Magrab 2009 % (1 153) % (1 5) % (153 5) % (1 5) % (5 2) 80

An Engineer’s Guide to MATLAB Chapter 2 which, upon execution, gives compare = 0. 0000 1. 0021 0. 5000 0. 8889 1. 0000 0. 6501 1. 5000 0. 4272 2. 0000 0. 2679 x approx Copyright © Edward B. Magrab 2009 1. 0000 0. 8868 0. 6481 0. 4251 0. 2658 sech(x) 0. 2080 0. 2346 0. 3210 0. 4894 0. 7827 % error 81

An Engineer’s Guide to MATLAB Chapter 2 Mathematical Operations with Matrices Addition and Subtraction If we have two matrices A and B, each of the order (m n), then The MATLAB expression for matrix addition or subtraction is W = A + B or W = A – B Copyright © Edward B. Magrab 2009 82

An Engineer’s Guide to MATLAB Chapter 2 Multiplication If we have an (m k) matrix A and a (k n) matrix B, then where For the conditions stated, the MATLAB expression for matrix multiplication is W = A*B Copyright © Edward B. Magrab 2009 83

An Engineer’s Guide to MATLAB Chapter 2 Note: The product of two matrices is defined only when the adjacent integers of their respective orders are equal; k in this case. In other words, (m k)(k n) (m n) where the notation indicates that we have summed the k terms. Matrix Transpose It can be shown that if C = AB, then its transpose is If A is an identity matrix (A = I) and m = n, then Copyright © Edward B. Magrab 2009 84

An Engineer’s Guide to MATLAB Chapter 2 Example – We shall multiply the following two matrices and show numerically that the transpose can be obtained either of the two ways indicated previously. The script is A = [11, 12, 13; 21, 22, 23]; B = [11, 12; 21, 22; 31, 32]; C = A*B Ctran 1 = C' Ctran 2 = B'*A' Copyright © Edward B. Magrab 2009 85

An Engineer’s Guide to MATLAB Chapter 2 Upon execution, we obtain C= 776 1406 Ctran 1 = 776 812 Ctran 2 = 776 812 Copyright © Edward B. Magrab 2009 812 1472 1406 1472 A = [11, 12, 13; 21, 22, 23]; B = [11, 12; 21, 22; 31, 32]; C = A*B Ctran 1 = C' Ctran 2 = B'*A' 1406 1472 86

An Engineer’s Guide to MATLAB Chapter 2 Now consider the following series Suppose that we are interested in the value of w(x, y) over a range of values for x and y: x = x 1, x 2, …, xm and y = y 1, y 2, …, yn. Then one can consider as one element of a matrix W of order (m n) as follows. Let F be a matrix of order (m k) Copyright © Edward B. Magrab 2009 87

An Engineer’s Guide to MATLAB Chapter 2 and G be a matrix of order

An Engineer’s Guide to MATLAB Chapter 2 Thus, matrix multiplication performs the summation of the series at each combination of values for x and y. We now consider three special cases of this general matrix multiplication: 1. The product of a row and a column vector 2. The product of a column and a row vector 3. The product of a row vector and a matrix Copyright © Edward B. Magrab 2009 89

An Engineer’s Guide to MATLAB Chapter 2 Product of a Row Vector and Column Vector Let a be the row vector a = [a 1 a 2 … ak] (1 k) and b be the column vector b = [b 1 b 2 … bk] (k 1) Then the product d = ab is the scalar (1 k)(k 1) l =1 and p = 1 Copyright © Edward B. Magrab 2009 90

An Engineer’s Guide to MATLAB Chapter 2 This is called the dot product of

An Engineer’s Guide to MATLAB Chapter 2 Product of a Column and Row Vector Let a be an (m 1) column vector and b a (1 n) row vector. Then the product H = ba is The elements of H, which are hij = biaj, are the individual products of all the combinations of the elements of b and a. l = 1, 2, …, m p = 1, 2, …, n Copyright © Edward B. Magrab 2009 92

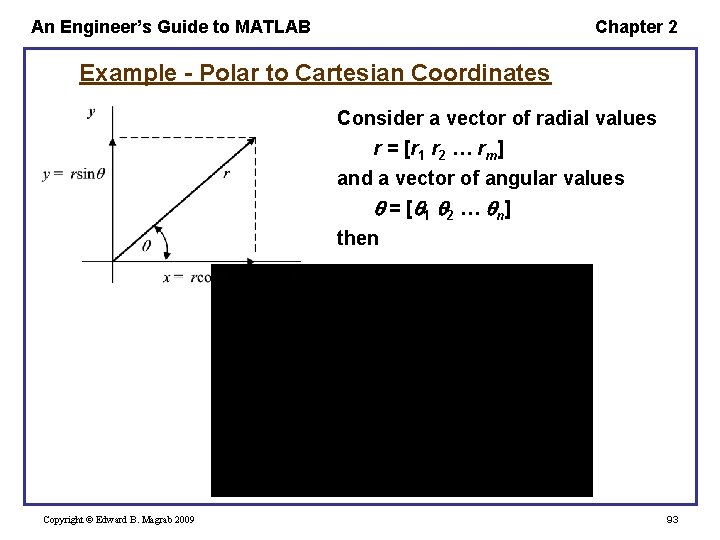
An Engineer’s Guide to MATLAB Chapter 2 Example - Polar to Cartesian Coordinates Consider a vector of radial values r = [r 1 r 2 … rm] and a vector of angular values = [ 1 2 … n ] then Copyright © Edward B. Magrab 2009 93

An Engineer’s Guide to MATLAB Chapter 2 and A typical MATLAB program would look like r = [0: 0. 05: 1]'; phi = 0: pi/20: 2*pi; x = r*cos(phi); y = r*sin(phi); Copyright © Edward B. Magrab 2009 % (21 1) % (1 41) % (21 41) 94

An Engineer’s Guide to MATLAB Chapter 2 Product of a Row Vector and a Matrix Let B be an (m n) matrix and a a (1 m) row vector. Then, the product g = a. B is l=1 p = 1, 2, …, n Copyright © Edward B. Magrab 2009 95

An Engineer’s Guide to MATLAB Chapter 2 Now consider the series Suppose that we are interested in the value of r(x) over a range of values x 1, x 2, …, xn. Then is one element of a vector r of order (1 n) as follows. Let p be a vector of order (1 m) with elements pk and V be the (m n) matrix Copyright © Edward B. Magrab 2009 96

An Engineer’s Guide to MATLAB Chapter 2 Then, r = p. V gives Copyright

An Engineer’s Guide to MATLAB Chapter 2 Example - Summation of a Fourier Series The Fourier series representation of a rectangular pulse of duration d and period T is given by where = t/T. Let us sum 150 terms of f( ) (K = 150) and plot it from 1/2 ≤ ≤ 1/2 when d/T = 0. 25. We see that Copyright © Edward B. Magrab 2009 98

An Engineer’s Guide to MATLAB Chapter 2 The program is k = 1: 150; % (1 150) tau = linspace(-0. 5, 100); % (1 100) sk = sin(pi*k/4). /(pi*k/4); % (1 150) cntau = cos(2*pi*k'*tau); % (150 100) f = 0. 25*(1+2*sk*cntau); % (1 150) (150 100) (1 100) plot(tau, f) Copyright © Edward B. Magrab 2009 99

An Engineer’s Guide to MATLAB Chapter 2 Example - Assume that the length of

An Engineer’s Guide to MATLAB Chapter 2 In order to have the matrices compatible

An Engineer’s Guide to MATLAB Chapter 2 Now we take the transpose and perform matrix multiplication From the matrix multiplication of these two expressions, we are summing over n, which is what we set out to do. Copyright © Edward B. Magrab 2009 102

An Engineer’s Guide to MATLAB n = (1: 25)*pi; eta = 0: 0. 025: 1; xi = 0: 0. 05: 0. 7; [X 1, temp 1] = meshgrid(xi, (1 -cos(n)). /n. ^3); temp 2 = exp(-n'*xi); Rnx = temp 1. *temp 2; temp 3 = sin(n'*eta); u = 4*Rnx'*temp 3; mesh(eta, xi, u) Copyright © Edward B. Magrab 2009 Chapter 2 % (1 25) % (1 41) % (1 15) % (25 41) % (15 41) 103

An Engineer’s Guide to MATLAB Chapter 2 Determinants A determinant of an array A

An Engineer’s Guide to MATLAB Chapter 2 The MATLAB expression for the determinant is det(a) Example – If A is defined as then the determinant of A is obtained from A = [1, 3; 4, 2]; d = det(A) which, upon execution, gives d= -10 Copyright © Edward B. Magrab 2009 105

An Engineer’s Guide to MATLAB Chapter 2 A class of problems, called eigenvalue problems, results in a determinant of the form where A and B are (n n) matrices and j, j = 1, 2, , …, n are the roots (called eigenvalues) of this equation. One form of the MATLAB expression to obtain is lambda = eig(A, B) Copyright © Edward B. Magrab 2009 106

An Engineer’s Guide to MATLAB Chapter 2 Example - Eigenvalues of a Spring-Mass System The eigenvalues of a three-degree-of-freedom springmass system are obtained from the characteristic equation where and Copyright © Edward B. Magrab 2009 107

An Engineer’s Guide to MATLAB Chapter 2 The program is K = [50, -30, 0; -30, 70, -40; 0, -40, 50]; M = diag([3, 1. 4, 5]); w = sqrt(eig(K, M)) which, upon execution, gives w= 1. 6734 3. 7772 7. 7201 % rad/s Copyright © Edward B. Magrab 2009 108

An Engineer’s Guide to MATLAB Chapter 2 Matrix Inverse The inverse of a square matrix A is an operation such that provided that A is not singular, that is, its determinant is not equal to zero (|A| 0). The expression for obtaining the inverse of matrix A is either inv(A) or A^-1 Note: 1/A A^-1; 1/A will cause the system to respond with an error message. However, 1. /A is valid, but it is not the inverse. Copyright © Edward B. Magrab 2009 109

An Engineer’s Guide to MATLAB Chapter 2 Example - Inverse of Matrix We shall determine the inverse of the magic matrix and the product of the inverse with the original matrix. The program is inv. M = inv(magic(3)) Ident. Mat = inv. M*magic(3) Its execution gives inv. M = 0. 1472 -0. 1444 0. 0639 -0. 0611 0. 0222 0. 1056 -0. 0194 0. 1889 -0. 1028 Ident. Mat = 1. 0000 0 -0. 0000 0 1. 0000 0 0 0. 0000 1. 0000 Copyright © Edward B. Magrab 2009 110

An Engineer’s Guide to MATLAB Chapter 2 Solution of a System of Equations Consider the following system of n equations and n unknowns xk, k = 1, 2, …, n We rewrite this system of equations in matrix notation as follows: Ax = b where A is the following (n n) matrix Copyright © Edward B. Magrab 2009 111

An Engineer’s Guide to MATLAB Chapter 2 and The symbolic solution is obtained by pre-multiplying both sides of the matrix equation by A-1. Thus, since A-1 A = I, the identity matrix, and Ix = x. Copyright © Edward B. Magrab 2009 112

An Engineer’s Guide to MATLAB Chapter 2 The preferred expression for solving this system of equations is x = Ab where the backslash operator indicates matrix division and is referred to by MATLAB as left matrix divide. An equivalent way of solving a system of equations is by using x = linsolve(A, b) Copyright © Edward B. Magrab 2009 113

An Engineer’s Guide to MATLAB Chapter 2 Example – Consider the following system of equations which, in matrix notation, is We shall determine xk and verify the results. Copyright © Edward B. Magrab 2009 114

An Engineer’s Guide to MATLAB Chapter 2 A = [8, 1, 6; 3, 5, 7; 4, 9, 2]; b = [7. 5, 4, 12]'; x = Ab z = A*x which, upon execution, gives x= 1. 2931 0. 8972 -0. 6236 z= 7. 5000 4. 0000 12. 0000 Copyright © Edward B. Magrab 2009 115

An Engineer’s Guide to MATLAB Chapter 2 Example – Temperatures in a Slab A thin square metal plate has a uniform temperature of 80 C on two opposite edges and a temperature of 120 C on the third edge and a temperature of 60 C on the remaining edge. A mathematical procedure to approximate the temperature at six uniformly spaced interior points results in the following equations. Copyright © Edward B. Magrab 2009 116

An Engineer’s Guide to MATLAB Chapter 2 The temperatures are determined from the following script. c = [4 -1 0 0 0 -1 -1 4 -1 0 0 -1 4 -1 0 0 -1 4 -1 -1 0 0 0 -1 4]; d = [200, 80, 140, 80, 200]; T = linsolve(c, d') The execution of this script gives Copyright © Edward B. Magrab 2009 T= 94. 2857 82. 8571 74. 2857 82. 8571 94. 2857 117