An Efficient Numerical Technique for Gradient Computation with

An Efficient Numerical Technique for Gradient Computation with Full -Wave EM Solvers Shirook M. Ali* and Natalia K. Nikolova * e-mail: alis 5@mcmaster. ca tel: (905) 525 9140 ext. 27762 fax: (905) 523 4407 Mc. Master University Department of Electrical and Computer Engineering Computational Electromagnetics Laboratory

Objectives and Outline Ø Optimization using gradient-based methods adjoint-sensitivity analysis: objectives obtain the response and its gradient with two fullwave analyses for all the design parameters, remeshing is not necessary Ø Adjoint variable method in full-wave analysis computational efficiency, feasibility, and accuracy Ø Applications with the frequency-domain TLM Ø Conclusions

Optimization via gradient-based methods The design problem - scalar objective function - design parameters - state variables objective

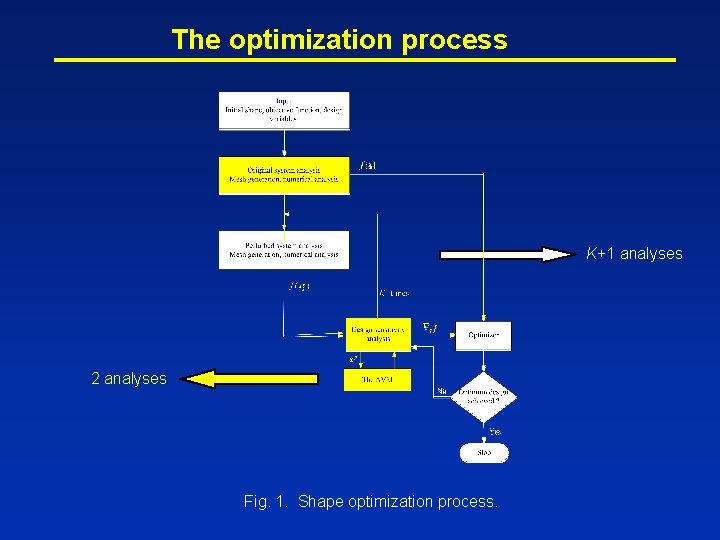
The optimization process K+1 analyses 2 analyses Fig. 1. Shape optimization process.

Adjoint Sensitivities of Linear Systems response function sensitivity: the adjoint variable method (AVM) [E. J. Haug et al. , Design Sensitivity Analysis of Structural Systems, 1986], [J. W. Banler, Optimization, vol. 1, 1994]

Adjoint Sensitivities of Linear Systems

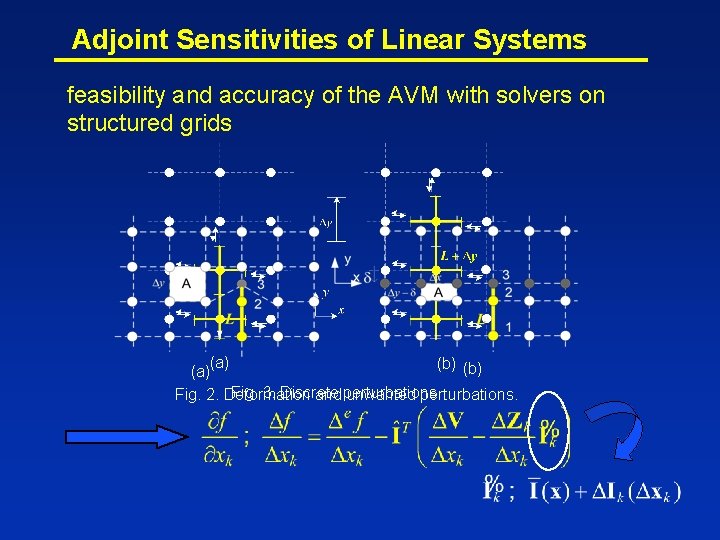
Adjoint Sensitivities of Linear Systems feasibility and accuracy of the AVM with solvers on structured grids (a) (b) (a) Fig. 3. Discrete Fig. 2. Deformation and perturbations. unwanted perturbations.

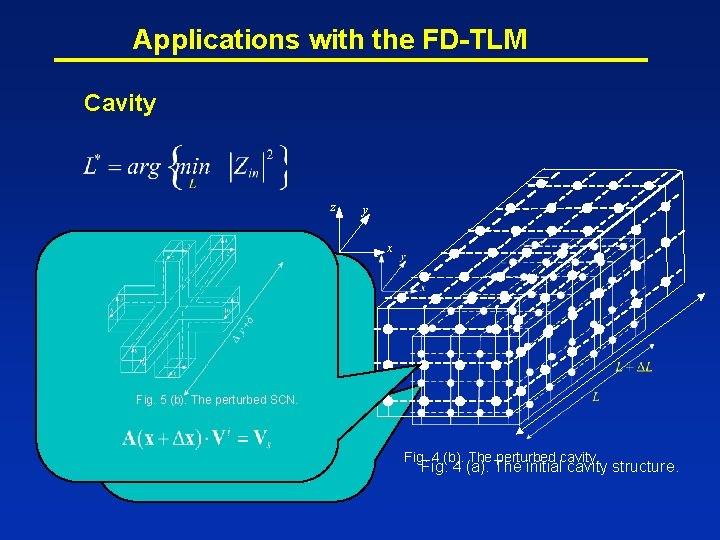
Applications with the FD-TLM Cavity z y x 12 7 4 2 11 3 6 10 8 9 1 Fig. 5 (b). The perturbed SCN. 5 Fig. 5 (a). The SCN. Fig. 4 (b). The perturbed cavity. Fig. 4 (a). The initial cavity structure.

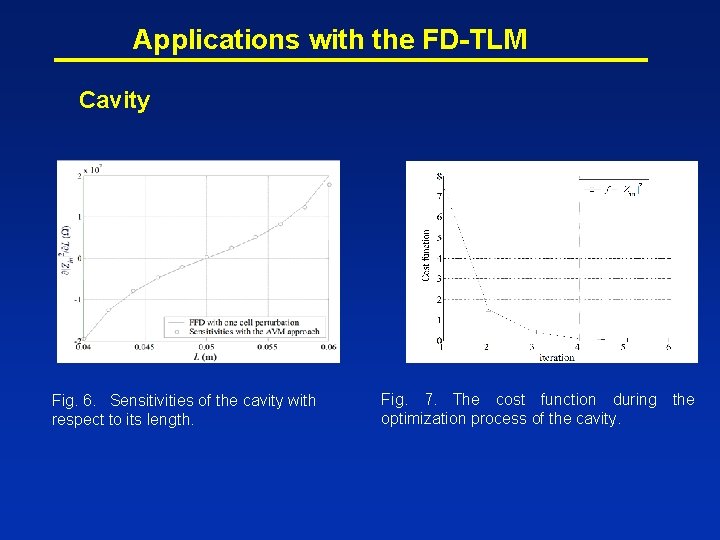
Applications with the FD-TLM Cavity Fig. 6. Sensitivities of the cavity with respect to its length. Fig. 7. The cost function during the optimization process of the cavity.

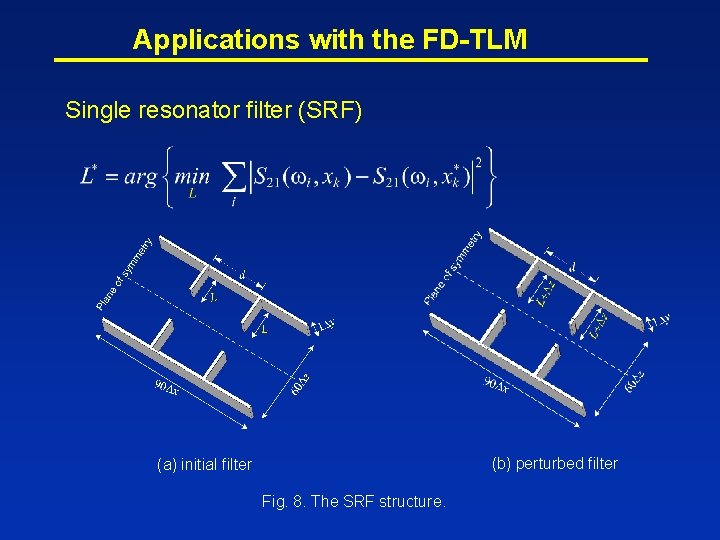
Applications with the FD-TLM Single resonator filter (SRF) (b) perturbed filter (a) initial filter Fig. 8. The SRF structure.

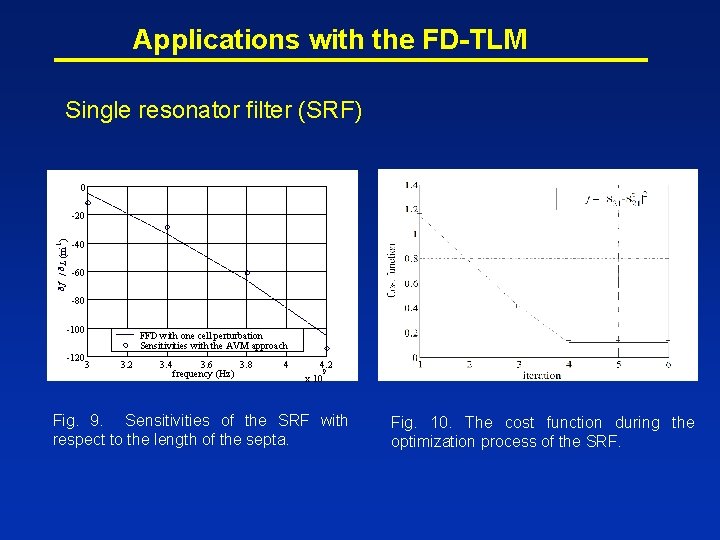
Applications with the FD-TLM Single resonator filter (SRF) 0 ¶ f / ¶ L (m-1 ) -20 -40 -60 -80 -100 -120 FFD with one cell perturbation Sensitivities with the AVM approach 3 3. 2 3. 4 3. 6 3. 8 frequency (Hz) 4 4. 2 9 x 10 Fig. 9. Sensitivities of the SRF with respect to the length of the septa. Fig. 10. The cost function during the optimization process of the SRF.

Conclusions The AVM is implemented into a feasible technique for frequency domain DSA of HF structures ü Reduction in the CPU time requirement by a factor of K ü Feasibility: does not require re-meshing during the optimization process ü Improved accuracy and convergence Factors affecting the accuracy ü Perturbation step size ü Finite differences for the computation of the gradients