An ApproximationBased Data Structure for Similarity Search R

An Approximation-Based Data Structure for Similarity Search R. Weber, S. Blott Hermes, 1998 Sistemi Informativi per le Decisioni Diego Cera – Michele Degli Esposti – Letizia Falcone 1

Dall’R-tree al VA-File I metodi di data-partitioning degradano all’aumentare delle dimensioni dello spazio vettoriale. Soluzione: Cos’è? Vector-Approximation FILE È un file che contiene un’approssimazione compatta e geometrica di ciascun vettore. Usualmente le approssimazioni occupano solo il 10 -20% dello spazio occupato dai vettori stessi. Perché lo usiamo? 15/03/2006 Il vantaggio principale riguarda le buone prestazioni all’aumentare della dimensionalità. Si può dimostrare che gli algoritmi basati sul VAfile sono più performanti, rispetto ai metodi di data-partitioning, di almeno un ordine di grandezza. An Approximation-Based Data Structure for Similarity Search 2

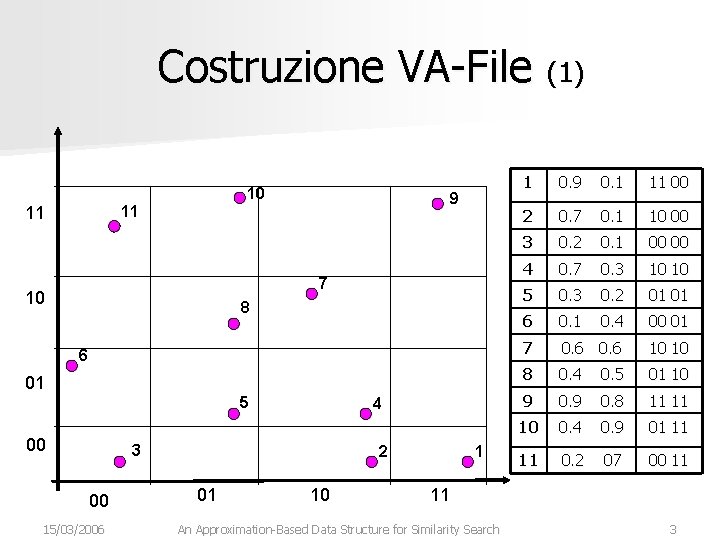
Costruzione VA-File (1) 10 9 11 11 7 10 8 6 01 5 00 4 3 00 15/03/2006 2 01 10 1 1 0. 9 0. 1 11 00 2 0. 7 0. 1 10 00 3 0. 2 0. 1 00 00 4 0. 7 0. 3 10 10 5 0. 3 0. 2 01 01 6 0. 1 0. 4 00 01 7 0. 6 10 10 8 0. 4 0. 5 01 10 9 0. 8 11 11 10 0. 4 0. 9 01 11 11 0. 2 07 00 11 11 An Approximation-Based Data Structure for Similarity Search 3

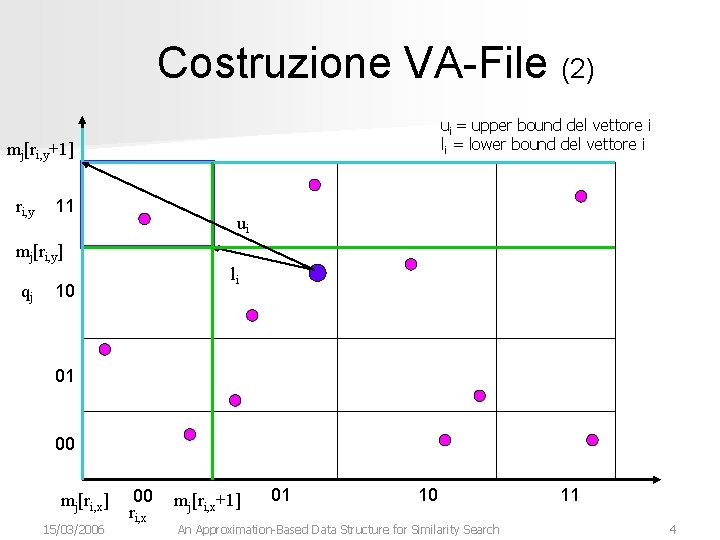
Costruzione VA-File (2) ui = upper bound del vettore i li = lower bound del vettore i mj[ri, y+1] ri, y 11 ui mj[ri, y] qj li 10 01 00 mj[ri, x] 15/03/2006 00 ri, x mj[ri, x+1] 01 10 An Approximation-Based Data Structure for Similarity Search 11 4

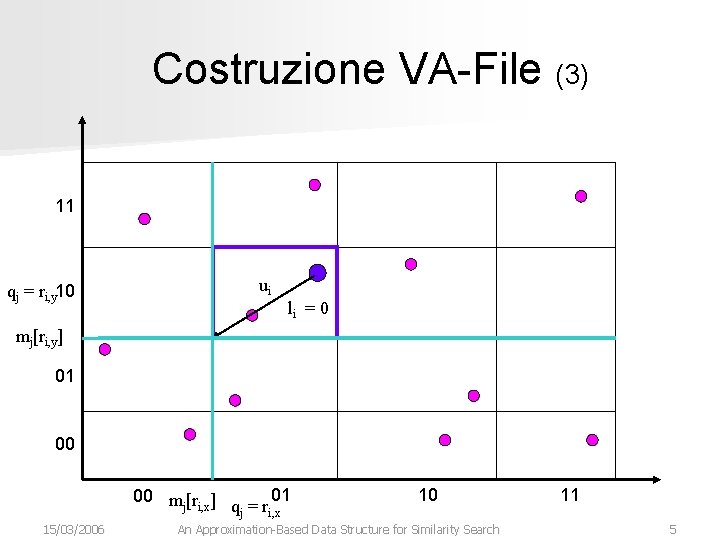
Costruzione VA-File (3) 11 qj = ri, y 10 ui li = 0 mj[ri, y] 01 00 mj[ri, x] qj = ri, x 15/03/2006 10 An Approximation-Based Data Structure for Similarity Search 11 5

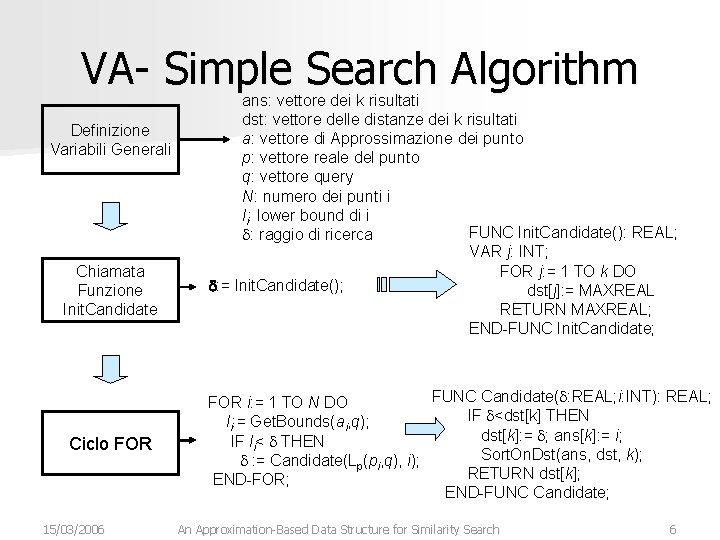
VA- Simple Search Algorithm Definizione Variabili Generali Chiamata Funzione Init. Candidate Ciclo FOR 15/03/2006 ans: vettore dei k risultati dst: vettore delle distanze dei k risultati a: vettore di Approssimazione dei punto p: vettore reale del punto q: vettore query N: numero dei punti i li: lower bound di i FUNC Init. Candidate(): REAL; d: raggio di ricerca VAR j: INT; FOR j: = 1 TO k DO d: = Init. Candidate(); dst[j]: = MAXREAL RETURN MAXREAL; END-FUNC Init. Candidate; FUNC Candidate(d: REAL; i: INT): REAL; FOR i: = 1 TO N DO IF d<dst[k] THEN li: = Get. Bounds(ai, q); dst[k]: = d; ans[k]: = i; IF li< d THEN Sort. On. Dst(ans, dst, k); d : = Candidate(Lp(pi, q), i); RETURN dst[k]; END-FOR; END-FUNC Candidate; An Approximation-Based Data Structure for Similarity Search 6

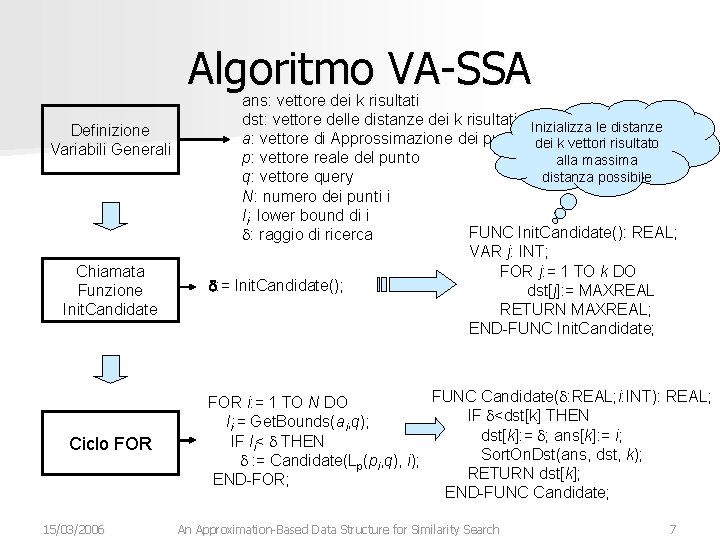
Algoritmo VA-SSA Definizione Variabili Generali Chiamata Funzione Init. Candidate Ciclo FOR 15/03/2006 ans: vettore dei k risultati dst: vettore delle distanze dei k risultati Inizializza le distanze a: vettore di Approssimazione dei punto dei k vettori risultato p: vettore reale del punto alla massima distanza possibile q: vettore query N: numero dei punti i li: lower bound di i FUNC Init. Candidate(): REAL; d: raggio di ricerca VAR j: INT; FOR j: = 1 TO k DO d: = Init. Candidate(); dst[j]: = MAXREAL RETURN MAXREAL; END-FUNC Init. Candidate; FUNC Candidate(d: REAL; i: INT): REAL; FOR i: = 1 TO N DO IF d<dst[k] THEN li: = Get. Bounds(ai, q); dst[k]: = d; ans[k]: = i; IF li< d THEN Sort. On. Dst(ans, dst, k); d : = Candidate(Lp(pi, q), i); RETURN dst[k]; END-FOR; END-FUNC Candidate; An Approximation-Based Data Structure for Similarity Search 7

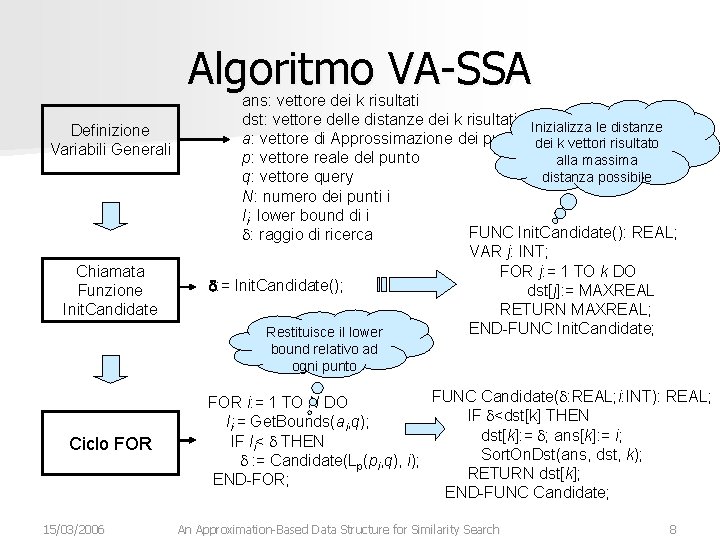
Algoritmo VA-SSA Definizione Variabili Generali Chiamata Funzione Init. Candidate ans: vettore dei k risultati dst: vettore delle distanze dei k risultati Inizializza le distanze a: vettore di Approssimazione dei punto dei k vettori risultato p: vettore reale del punto alla massima distanza possibile q: vettore query N: numero dei punti i li: lower bound di i FUNC Init. Candidate(): REAL; d: raggio di ricerca VAR j: INT; FOR j: = 1 TO k DO d: = Init. Candidate(); dst[j]: = MAXREAL RETURN MAXREAL; END-FUNC Init. Candidate; Restituisce il lower bound relativo ad ogni punto Ciclo FOR 15/03/2006 FUNC Candidate(d: REAL; i: INT): REAL; FOR i: = 1 TO N DO IF d<dst[k] THEN li: = Get. Bounds(ai, q); dst[k]: = d; ans[k]: = i; IF li< d THEN Sort. On. Dst(ans, dst, k); d : = Candidate(Lp(pi, q), i); RETURN dst[k]; END-FOR; END-FUNC Candidate; An Approximation-Based Data Structure for Similarity Search 8

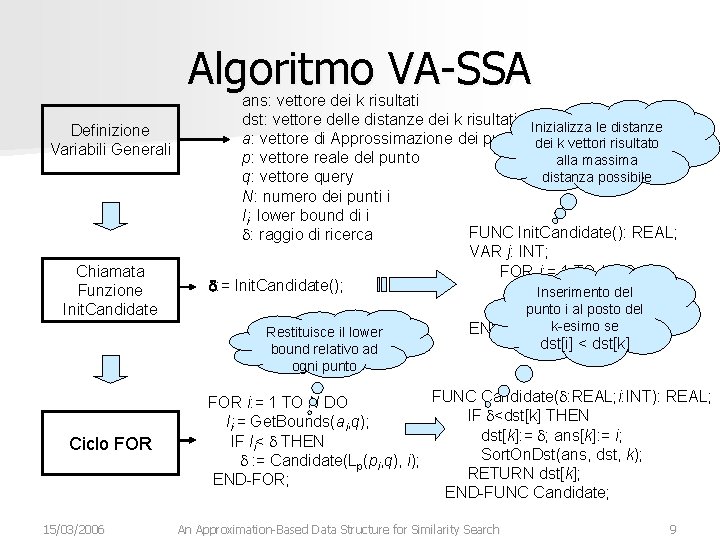
Algoritmo VA-SSA Definizione Variabili Generali Chiamata Funzione Init. Candidate ans: vettore dei k risultati dst: vettore delle distanze dei k risultati Inizializza le distanze a: vettore di Approssimazione dei punto dei k vettori risultato p: vettore reale del punto alla massima distanza possibile q: vettore query N: numero dei punti i li: lower bound di i FUNC Init. Candidate(): REAL; d: raggio di ricerca VAR j: INT; FOR j: = 1 TO k DO d: = Init. Candidate(); dst[j]: = MAXREAL Inserimento del punto i MAXREAL; al posto del RETURN se END-FUNCk-esimo Init. Candidate; Restituisce il lower dst[i] < dst[k] bound relativo ad ogni punto Ciclo FOR 15/03/2006 FUNC Candidate(d: REAL; i: INT): REAL; FOR i: = 1 TO N DO IF d<dst[k] THEN li: = Get. Bounds(ai, q); dst[k]: = d; ans[k]: = i; IF li< d THEN Sort. On. Dst(ans, dst, k); d : = Candidate(Lp(pi, q), i); RETURN dst[k]; END-FOR; END-FUNC Candidate; An Approximation-Based Data Structure for Similarity Search 9

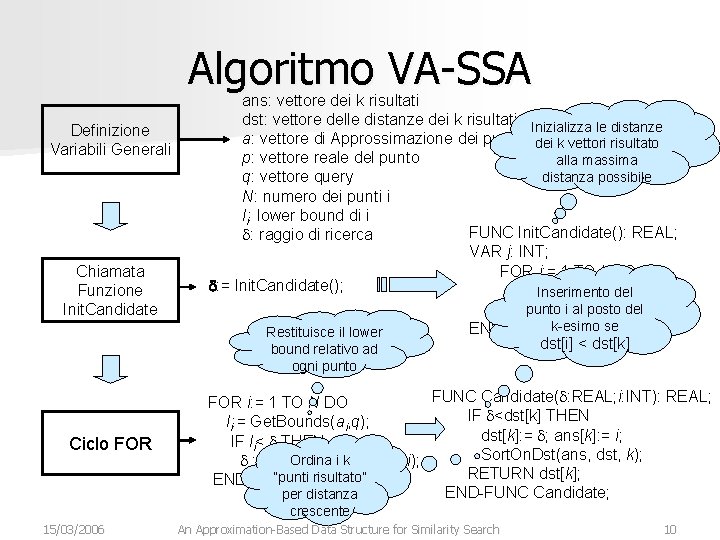
Algoritmo VA-SSA Definizione Variabili Generali Chiamata Funzione Init. Candidate ans: vettore dei k risultati dst: vettore delle distanze dei k risultati Inizializza le distanze a: vettore di Approssimazione dei punto dei k vettori risultato p: vettore reale del punto alla massima distanza possibile q: vettore query N: numero dei punti i li: lower bound di i FUNC Init. Candidate(): REAL; d: raggio di ricerca VAR j: INT; FOR j: = 1 TO k DO d: = Init. Candidate(); dst[j]: = MAXREAL Inserimento del punto i MAXREAL; al posto del RETURN se END-FUNCk-esimo Init. Candidate; Restituisce il lower dst[i] < dst[k] bound relativo ad ogni punto Ciclo FOR FUNC Candidate(d: REAL; i: INT): REAL; FOR i: = 1 TO N DO IF d<dst[k] THEN li: = Get. Bounds(ai, q); dst[k]: = d; ans[k]: = i; IF li< d THEN Sort. On. Dst(ans, dst, k); Ordina i k p(pi, q), i); d : = Candidate(L RETURN dst[k]; “punti risultato” END-FOR; END-FUNC Candidate; per distanza crescente 15/03/2006 An Approximation-Based Data Structure for Similarity Search 10

VA-SSA Hp: k=3 Dst[1] Dst[2] Dst[3] =MR =L = Lp 1 p 3 p 2 =LLp 2 p 1 =MR =L = LMR p 1 p 2 p 3 d=MAXREAL d= Lp 1 11 q 10 l 3 < d Lp 3 3 < Dst[3] a 3 l 2 < d 01 00 15/03/2006 Lp 2 < Dst[3] l <d 1 2 a 2 Lp 1< Dst[3] 1 01 Structure for Similarity 10 An 00 Approximation-Based Data Search a 1 11 11

VA-SSA Hp: k=3 Dst[1] Dst Dst[2] Dst[3] ==LLp 3 p 3 =L =Lp 4 p 2 = Lp 4 =L p 1 p 2 d= Lp 1 11 l 4 = 0 10 q a 4 4 01 00 15/03/2006 3 a 3 Lp 4< Dst[3] 2 a 2 1 01 Structure for Similarity 10 An 00 Approximation-Based Data Search a 1 11 12

VA-SSA Hp: k=3 Dst[1] Dst[2] Dst[3] = Lp 3 = Lp 4 p 6 =L =LLp 4 p 6 = p 2 Punti più vicini: 3, 6, 4 d= Lp 2 a 6 6 11 Lp 6 < Dst[3] q a 4 10 l 6< d d= Lp 4 3 a 3 4 l 5 > d 01 2 a 5 00 15/03/2006 a 2 5 1 01 Structure for Similarity 10 An 00 Approximation-Based Data Search a 1 11 13

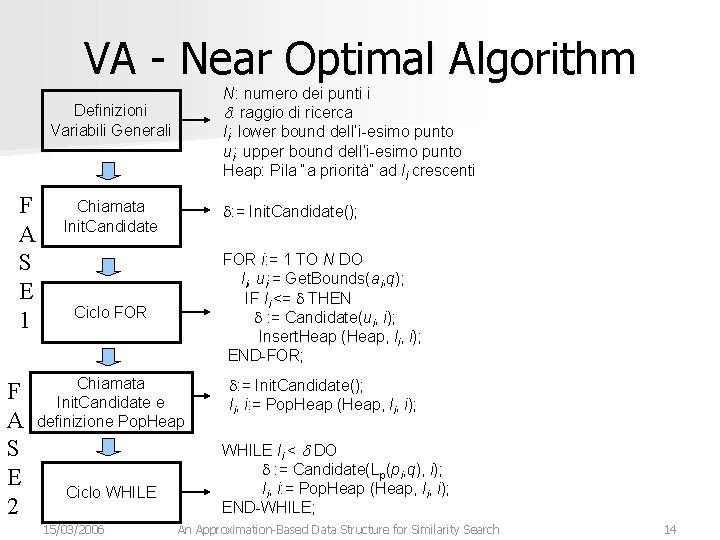
VA - Near Optimal Algorithm N: numero dei punti i d: raggio di ricerca li: lower bound dell’i-esimo punto ui: upper bound dell’i-esimo punto Heap: Pila “a priorità” ad li crescenti Definizioni Variabili Generali F A S E 1 F A S E 2 Chiamata Init. Candidate d: = Init. Candidate(); Ciclo FOR i: = 1 TO N DO li, ui: = Get. Bounds(ai, q); IF li <= d THEN d : = Candidate(ui, i); Insert. Heap (Heap, li, i); END-FOR; Chiamata Init. Candidate e definizione Pop. Heap d: = Init. Candidate(); li, i: = Pop. Heap (Heap, li, i); Ciclo WHILE 15/03/2006 WHILE li < d DO d : = Candidate(Lp(pi, q), i); li, i: = Pop. Heap (Heap, li, i); END-WHILE; An Approximation-Based Data Structure for Similarity Search 14

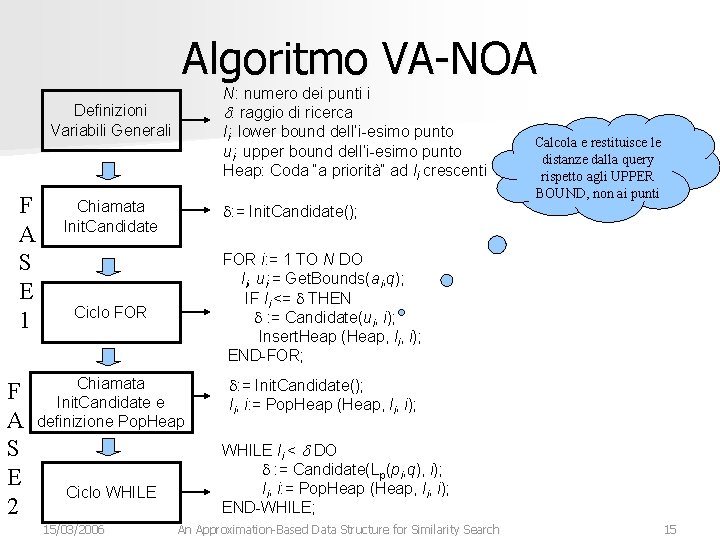
Algoritmo VA-NOA N: numero dei punti i d: raggio di ricerca li: lower bound dell’i-esimo punto ui: upper bound dell’i-esimo punto Heap: Coda “a priorità” ad li crescenti Definizioni Variabili Generali F A S E 1 F A S E 2 Chiamata Init. Candidate d: = Init. Candidate(); Ciclo FOR i: = 1 TO N DO li, ui: = Get. Bounds(ai, q); IF li <= d THEN d : = Candidate(ui, i); Insert. Heap (Heap, li, i); END-FOR; Chiamata Init. Candidate e definizione Pop. Heap d: = Init. Candidate(); li, i: = Pop. Heap (Heap, li, i); Ciclo WHILE 15/03/2006 Calcola e restituisce le distanze dalla query rispetto agli UPPER BOUND, non ai punti WHILE li < d DO d : = Candidate(Lp(pi, q), i); li, i: = Pop. Heap (Heap, li, i); END-WHILE; An Approximation-Based Data Structure for Similarity Search 15

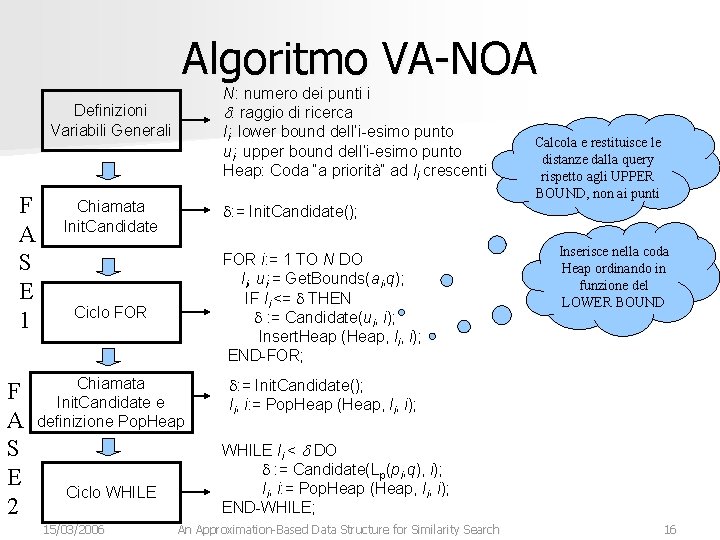
Algoritmo VA-NOA N: numero dei punti i d: raggio di ricerca li: lower bound dell’i-esimo punto ui: upper bound dell’i-esimo punto Heap: Coda “a priorità” ad li crescenti Definizioni Variabili Generali F A S E 1 F A S E 2 Chiamata Init. Candidate d: = Init. Candidate(); Ciclo FOR i: = 1 TO N DO li, ui: = Get. Bounds(ai, q); IF li <= d THEN d : = Candidate(ui, i); Insert. Heap (Heap, li, i); END-FOR; Chiamata Init. Candidate e definizione Pop. Heap d: = Init. Candidate(); li, i: = Pop. Heap (Heap, li, i); Ciclo WHILE 15/03/2006 Calcola e restituisce le distanze dalla query rispetto agli UPPER BOUND, non ai punti Inserisce nella coda Heap ordinando in funzione del LOWER BOUND WHILE li < d DO d : = Candidate(Lp(pi, q), i); li, i: = Pop. Heap (Heap, li, i); END-WHILE; An Approximation-Based Data Structure for Similarity Search 16

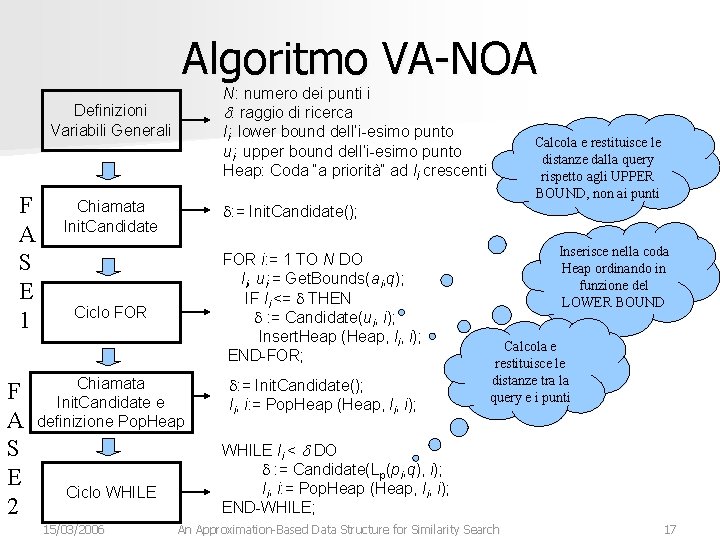
Algoritmo VA-NOA N: numero dei punti i d: raggio di ricerca li: lower bound dell’i-esimo punto ui: upper bound dell’i-esimo punto Heap: Coda “a priorità” ad li crescenti Definizioni Variabili Generali F A S E 1 F A S E 2 Chiamata Init. Candidate d: = Init. Candidate(); FOR i: = 1 TO N DO li, ui: = Get. Bounds(ai, q); IF li <= d THEN d : = Candidate(ui, i); Insert. Heap (Heap, li, i); END-FOR; Ciclo FOR Chiamata Init. Candidate e definizione Pop. Heap Ciclo WHILE 15/03/2006 Calcola e restituisce le distanze dalla query rispetto agli UPPER BOUND, non ai punti d: = Init. Candidate(); li, i: = Pop. Heap (Heap, li, i); Inserisce nella coda Heap ordinando in funzione del LOWER BOUND Calcola e restituisce le distanze tra la query e i punti WHILE li < d DO d : = Candidate(Lp(pi, q), i); li, i: = Pop. Heap (Heap, li, i); END-WHILE; An Approximation-Based Data Structure for Similarity Search 17

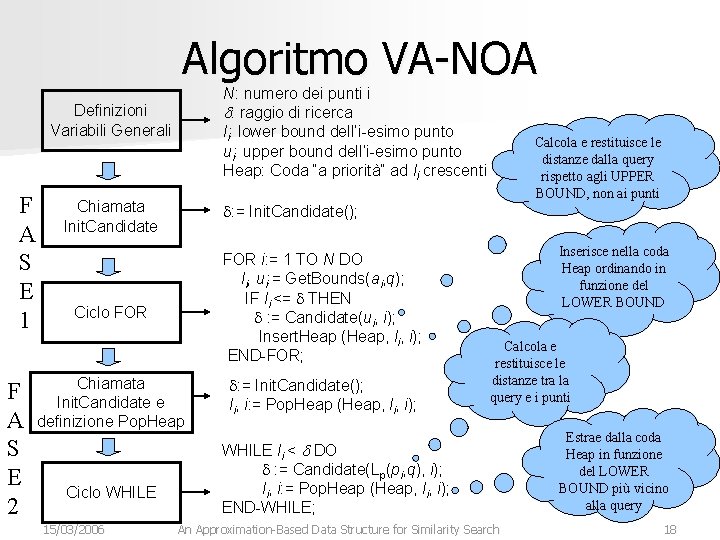
Algoritmo VA-NOA N: numero dei punti i d: raggio di ricerca li: lower bound dell’i-esimo punto ui: upper bound dell’i-esimo punto Heap: Coda “a priorità” ad li crescenti Definizioni Variabili Generali F A S E 1 F A S E 2 Chiamata Init. Candidate d: = Init. Candidate(); FOR i: = 1 TO N DO li, ui: = Get. Bounds(ai, q); IF li <= d THEN d : = Candidate(ui, i); Insert. Heap (Heap, li, i); END-FOR; Ciclo FOR Chiamata Init. Candidate e definizione Pop. Heap Ciclo WHILE 15/03/2006 Calcola e restituisce le distanze dalla query rispetto agli UPPER BOUND, non ai punti d: = Init. Candidate(); li, i: = Pop. Heap (Heap, li, i); Inserisce nella coda Heap ordinando in funzione del LOWER BOUND Calcola e restituisce le distanze tra la query e i punti WHILE li < d DO d : = Candidate(Lp(pi, q), i); li, i: = Pop. Heap (Heap, li, i); END-WHILE; An Approximation-Based Data Structure for Similarity Search Estrae dalla coda Heap in funzione del LOWER BOUND più vicino alla query 18

VA-NOA (Fase 1) Hp: k=3 Dst[1] Dst[2] Dst[3] =MR =u = u 12 =uu 31 =MR =u = MR u 13 2 Heap l 321 l 1 d=MAXREAL d= u 1 11 q l 3 < d 10 l 2 < d 01 00 15/03/2006 u 2 < Dst[3] l <d 1 2 a 2 3 a 3 u 3< Dst[3] u 1 < Dst[3] 1 01 Structure for Similarity 10 An 00 Approximation-Based Data Search a 1 11 19

VA-NOA (Fase 1) Hp: k=3 Dst[1] Dst Dst[2] Dst[3] ==uu 42 = u 413 =u =u =u 23 Heap l 43 l 32 l 21 l 1 d= u 3 d= u 1 11 l 4 = 0 10 q a 4 4 01 00 15/03/2006 3 a 3 u 4 < Dst[3] 2 a 2 1 01 Structure for Similarity 10 An 00 Approximation-Based Data Search a 1 11 20

VA-NOA (Fase 1) Hp: k=3 Dst[1] Dst[2] Dst[3] = u 4 =uu 262 = = u 263 Heap d= u 2 a 6 l 4 l 3 l 62 l 21 l 15 l 5 d= u 3 6 11 u 6 < Dst[3] q a 4 10 l 6< d 3 a 3 4 l 5 < d 01 2 a 5 00 15/03/2006 u 5 > Dst[3] a 2 5 1 01 Structure for Similarity 10 An 00 Approximation-Based Data Search a 1 11 21

VA-NOA (Fase 2) Hp: k=3 Dst[1] Dst[2] Dst[3] =Lp 4 =MR =L p 4 Heap l 4 l 3 l 6 l 2 l 1 l 5 d=MAXREAL 6 11 l 4 = 0 q 3 10 4 01 00 15/03/2006 2 5 1 01 Structure for Similarity 10 An 00 Approximation-Based Data Search 11 22

VA-NOA (Fase 2) Hp: k=3 Dst[1] Dst[2] Dst[3] =Lp 3 p 4 =Lp 4 =MR =L p 3 Heap l 3 l 6 l 2 l 1 l 5 d=MAXREAL 6 11 q l 3 < d 3 10 4 01 00 15/03/2006 2 5 1 01 Structure for Similarity 10 An 00 Approximation-Based Data Search 11 23

VA-NOA (Fase 2) Hp: k=3 Dst[1] Dst[2] Dst[3] =Lp 3 =Lp 6 p 4 = Lp 6 p 4 =MR =L Heap l 6 l 2 l 1 l 5 d=MAXREAL 6 11 d= Lp 4 l 6< d q 3 10 4 01 00 15/03/2006 2 5 1 01 Structure for Similarity 10 An 00 Approximation-Based Data Search 11 24

VA-NOA (Fase 2) Hp: k=3 Dst[1] Dst[2] Dst[3] =Lp 3 =Lp 6 = Lp 4 Heap 6 l 2 l 1 l 5 d= Lp 4 11 q 3 10 4 Lp 2 > Dst[3] 01 00 15/03/2006 l 2 < d 2 5 1 01 Structure for Similarity 10 An 00 Approximation-Based Data Search 11 25

VA-NOA (Fase 2) Hp: k=3 Dst[1] Dst[2] Dst[3] =Lp 3 =Lp 6 = Lp 4 Punti più vicini: 3, 6, 4 6 Heap l 1 l 5 d= Lp 4 11 q 3 10 4 01 00 15/03/2006 2 5 l 1> d 1 01 Structure for Similarity 10 An 00 Approximation-Based Data Search 11 26

Confronto VA-File ed R-Tree Algoritmi basati su VA-File non richiedono la costruzione di alcun albero - Algoritmi VA-File visitano sicuramente tutti i punti. . . +. . . Però ogni lettura è computazionalmente meno costosa + Algoritmi per i VA-File calcolano le distanze solo per i candidati + = Algoritmi sui VA-File migliorano all’aumentare delle dimensioni mentre gli R-Tree peggiorano 15/03/2006 An Approximation-Based Data Structure for Similarity Search 27

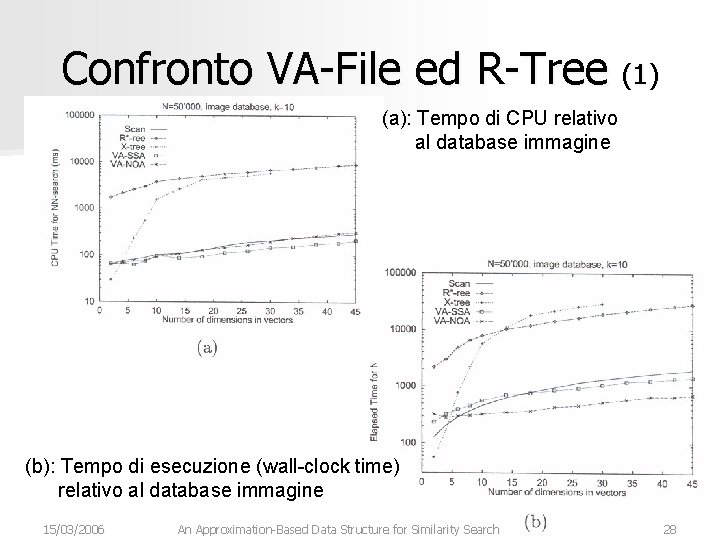
Confronto VA-File ed R-Tree (1) (a): Tempo di CPU relativo al database immagine (b): Tempo di esecuzione (wall-clock time) relativo al database immagine 15/03/2006 An Approximation-Based Data Structure for Similarity Search 28

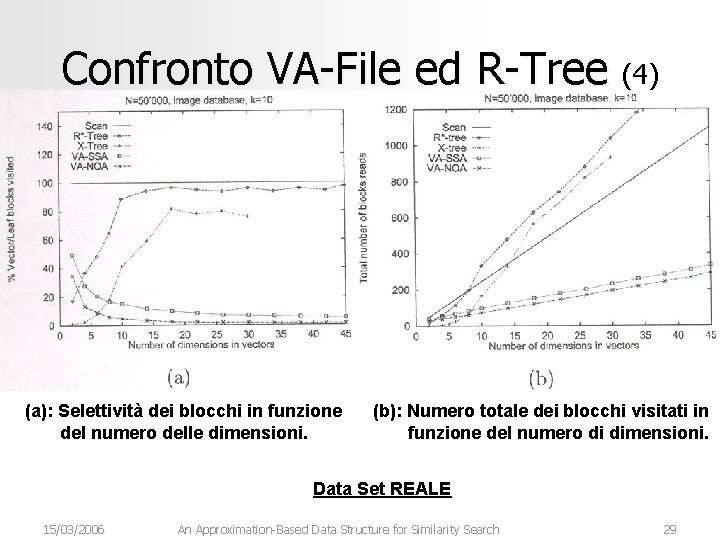
Confronto VA-File ed R-Tree (4) (a): Selettività dei blocchi in funzione del numero delle dimensioni. (b): Numero totale dei blocchi visitati in funzione del numero di dimensioni. Data Set REALE 15/03/2006 An Approximation-Based Data Structure for Similarity Search 29

Confronto tra VA-SSA e VA-NOA n VA-NOA visita due volte i punti nella pila. . . n. . . ma nella prima fase calcola solo gli upper bound n Difatti VA-NOA calcola Lp, la distanza pesata, su un numero ridotto di candidati n In pratica: – VA-SSA è di complessità O(N) – VA-NOA è di complessità O(N 2 log 2 N 1) 15/03/2006 An Approximation-Based Data Structure for Similarity Search 30

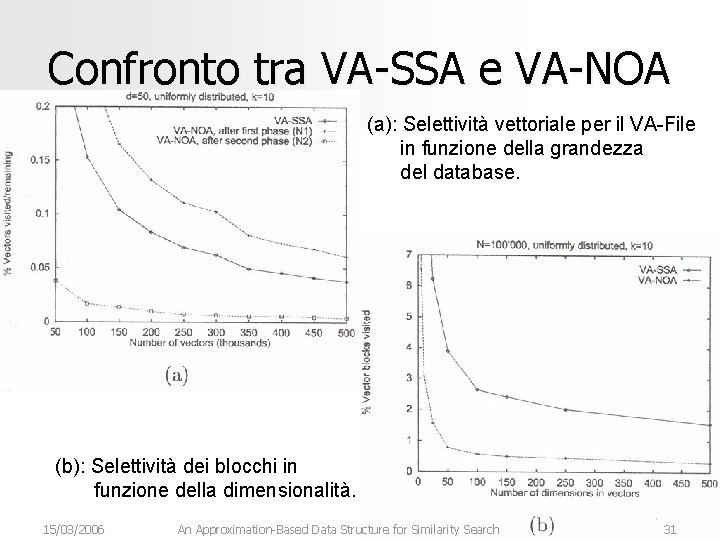
Confronto tra VA-SSA e VA-NOA (a): Selettività vettoriale per il VA-File in funzione della grandezza del database. (b): Selettività dei blocchi in funzione della dimensionalità. 15/03/2006 An Approximation-Based Data Structure for Similarity Search 31

Bibliografia n “An Approximation-Based Data Structure for Similarity Search” – R. Weber, S. Blott Hermes TR, 1998 n “Algorithms” – R. Sedgewick Addison-Wesley Publishing Company, 1983 15/03/2006 An Approximation-Based Data Structure for Similarity Search 32

Grazie per l’attenzione!! Diego Cera Michele Degli Esposti Letizia Falcone 33