An Approximation Algorithm for Binary Searching in Trees

An Approximation Algorithm for Binary Searching in Trees Marco Molinaro Carnegie Mellon University joint work with Eduardo Laber (PUC-Rio)

Searching in sorted lists n Sorted list of numbers n Marked number m n Find the marked number using queries ‘x ≤ m? ’ 3 5 6 10 14 . . .

Searching in sorted lists n n n Search strategy: procedure that indicates which number should be queried next Can be represented by a decision tree (DT) # queries to find m = path length 3 5 6 10 14 . . . 10 ≤ 14 > 3 ≤ 3 > 5 ≤ > 5 DT ≤ 66 ≤ 6 > 10 14 >

Searching in sorted lists n n n We are given the probability of each number being the marked one Expected number of queries of a strategy = expected path length of the corresponding decision tree Efficient strategy is one with minimum expected path 0, 05 0, 1 3 5 0. 2 0, 1 0, 5 . . . 6 10 14 . . . 10 ≤ 5 ≤ ≤ 3 > 14 > > ≤ ≤ 6 > 3 5 6 10 0, 05 0, 1 0, 2 0, 1 14 0, 5 >

Searching in trees n n Tree with exactly one marked node m We can query an arc and find out which endpoint is closer to the marked node

Searching in trees n n Search strategy: procedure that indicates which arc should be queried next Can be represented by a decision tree a b ~c c DT (c, d) ~d (a, b) d ~a (f, h) b f h ~h ~f ~b (d, f) ~d ~f f

Searching in trees n n n Search strategy: procedure that indicates which arc should be queried next Can be represented by a decision tree # queries to find m = path length a b ~c c DT (c, d) ~d (a, b) d ~a (f, h) b f h ~h ~f ~b (d, f) ~d ~f f

Searching in trees n n n We are given the probability of each node being the marked one Expected number of queries is the expected path length of the corresponding decision tree The goal is to find a DT with minimum expected path a ~c b (c, d) ~d c. 2 (a, b) . 1. 1. 3 d f h ~a (f, h) b . 2 ~h ~f ~b (d, f) ~d ~f f . 3

Searching in trees n n Def: Given a tree T and weights w, compute a decision tree for searching in T with minimum expected path from root to leaves w. r. t. w Motivation ¨ Generalizes searches in totally ordered structures to (one type of) partially ordered structures ¨ Application to software testing and filesystem synchronization

Related work n Searching in sorted lists ¨ Worst-case n Binary search is optimal ¨ Average-case Knuth [Acta Informatica 71]: O(n 2) n de Prisco, de Santis [IPL 93]: good approximation in linear time n

Related work n Searching in trees ¨ Worst-case Ben-Asher et al. [SIAM J. Comput. 99]: O(n 4 log 3 n) n Onak, Parys [FOCS 06]: O(n 3) n Mozes et al. [SODA 08]: O(n) n ¨ Average-case n Kosaraju et al. [WADS 99]: O(log n)-approximation

Related work n Searching in posets ¨ Worst-case Arkin et al. [Int. J. Comput. Geometry Appl. 98]: O(log n)-approximation n Carmo et al. [TCS 04] n Finding optimal strategy is NP-Hard ¨ Constant-factor approximation for random posets ¨ ¨ Average-case n Kosaraju et al. [WADS 99]: O(log n)-approximation

Our results First constant-factor approximation for searching in trees (average-case metric) n Linear running time n

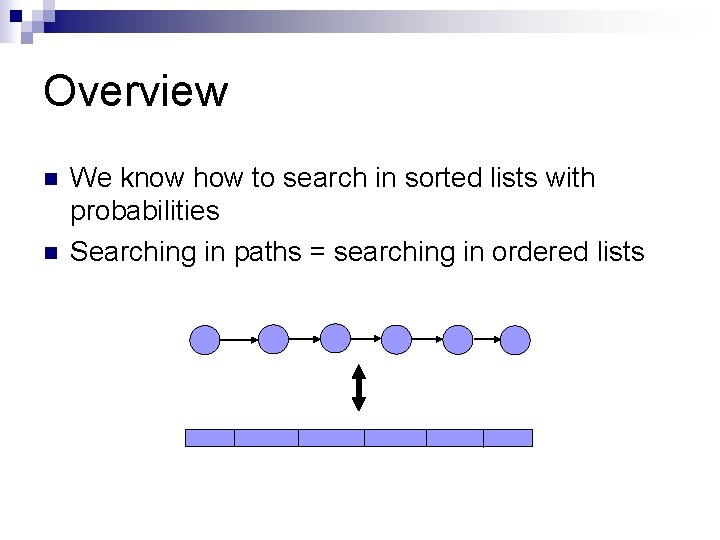
Overview n n We know how to search in sorted lists with probabilities Searching in paths = searching in ordered lists

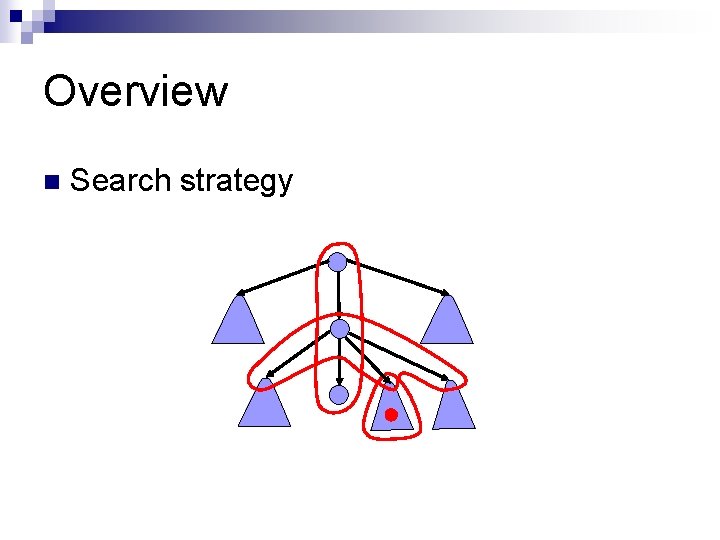
Overview n Search strategy

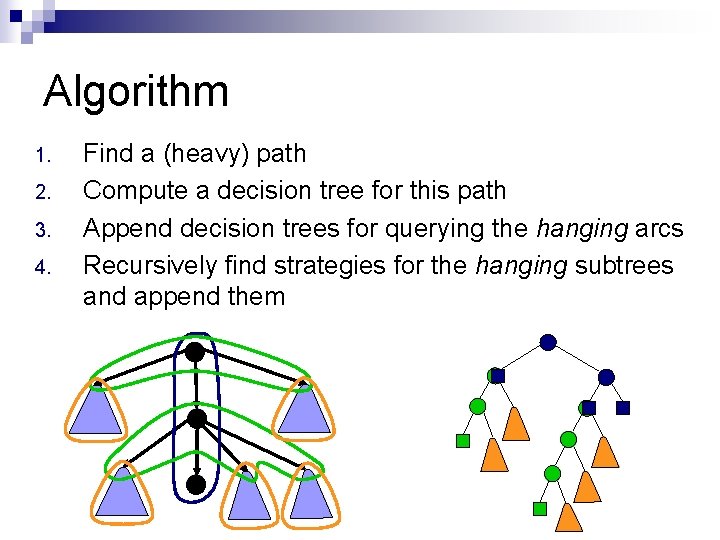
Algorithm 1. 2. 3. 4. Find a (heavy) path Compute a decision tree for this path Append decision trees for querying the hanging arcs Recursively find strategies for the hanging subtrees and append them

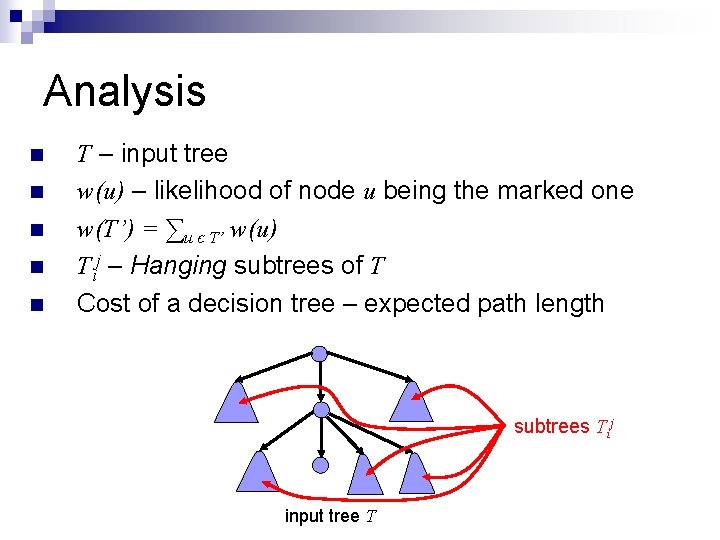
Analysis n n n T – input tree w(u) – likelihood of node u being the marked one w(T’) = ∑u є T’ w(u) Tij – Hanging subtrees of T Cost of a decision tree – expected path length subtrees Tij input tree T

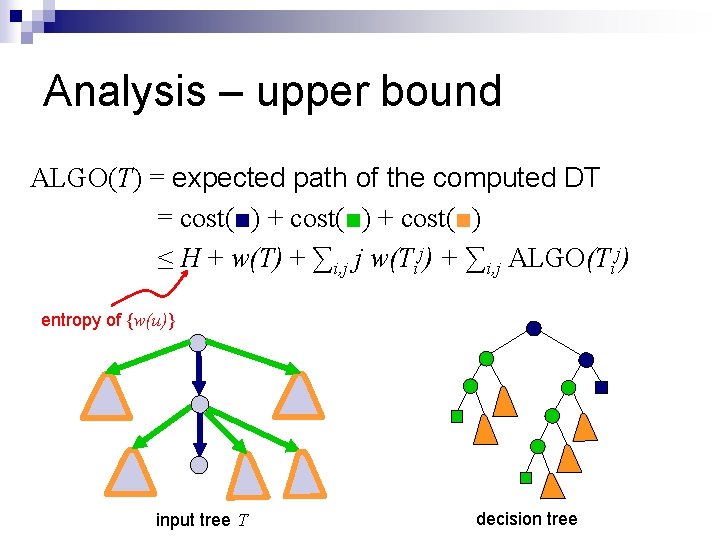
Analysis – upper bound ALGO(T) = expected path of the computed DT = cost(■) + cost(■) ≤ H + w(T) + ∑i, j j w(Tij) + ∑i, j ALGO(Tij) entropy of {w(u)} input tree T decision tree

Analysis – lower bounds UB: LB 1: LB 2: n n only when H is large When H >> w(T) ¨ UB and LB 1 When H ≤ w(T) ¨ UB and (LB 1 + LB 2) for all H, ALGO(T) ≤ α OPT(T)

Analysis – entropy lower bound n n OPT(T) = from root to (■) + from (■) to leaves from root to (■): using Shannon’s lossless coding theorem, we can lower bound by H / log 3 – w(T) from (■) to (■): ¨ There at most 2 purple nodes per level ¨ These paths cost ≥ from (■) to leaves: Every query to arcs in the trees Tij are descendants of purple nodes ¨ Costs at least as much as searching inside the trees Tij, namely ∑i, j OPT(Tij) ¨ D*

Analysis – alternative lower bound n n OPT(T) ≥ from root to (■) + from (■) to leaves from root to (■): Costs = ∑i, j distance to i-th purple node. w(Tij) ¨ At most one purple node can have distance 0 ¨ w(Tij) ≤ w(T)/2 ¨ Costs at least w(T)/2 ¨ n from (■) to leaves: ¨ Costs at least as much as searching inside the trees Tij, namely ∑i, j OPT(Tij) D*

Efficient implementation Most steps take linear time n In order to find a good strategy, the algorithm uses sorting of weights n ¨ Use n linear time approximate sorting The algorithm can be implemented in linear time

Conclusions n First constant-factor approximation for searching in trees (average-case) Linear running time n Open questions n ¨ Is searching in trees polynomially solvable? ¨ Improved approximations for more general posets

Thank you!