An Approach to ModelBased Control of Frictionally Constrained

An Approach to Model-Based Control of Frictionally Constrained Robots Aaron Greenfield CFR Talk 02 -22 -05 Biorobotics Lab

Talk Outline 1. Control Under Frictional Contact 2. Planar Dynamics Model - Multi-Rigid-Body - Coulomb Friction 3. Dynamic Response Calculation 4. Applications MOVIE: Real Rhex Flipping MOVIE: Real Snake Climbing (Saranli) (Borer) Slide 2 / 26

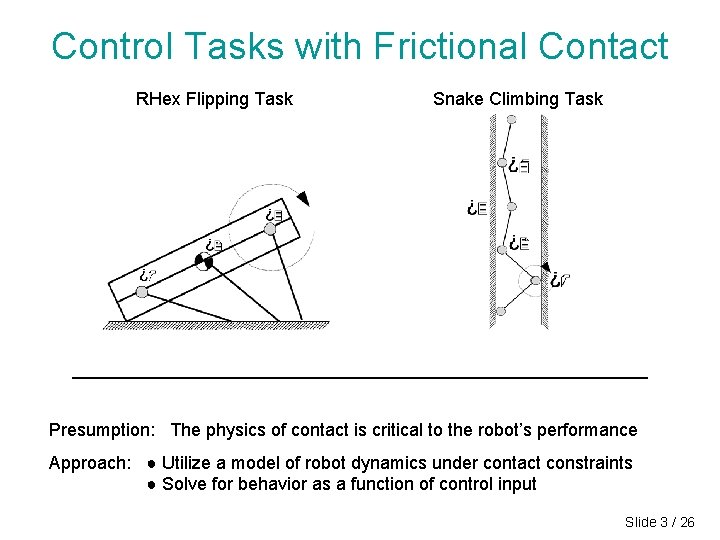
Control Tasks with Frictional Contact RHex Flipping Task Snake Climbing Task Presumption: The physics of contact is critical to the robot’s performance Approach: ● Utilize a model of robot dynamics under contact constraints ● Solve for behavior as a function of control input Slide 3 / 26

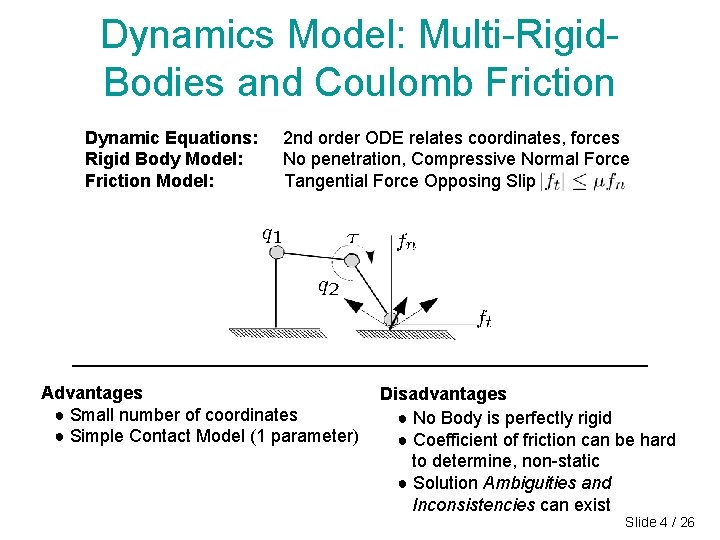
Dynamics Model: Multi-Rigid. Bodies and Coulomb Friction Dynamic Equations: Rigid Body Model: Friction Model: 2 nd order ODE relates coordinates, forces No penetration, Compressive Normal Force Tangential Force Opposing Slip Advantages ● Small number of coordinates ● Simple Contact Model (1 parameter) Disadvantages ● No Body is perfectly rigid ● Coefficient of friction can be hard to determine, non-static ● Solution Ambiguities and Inconsistencies can exist Slide 4 / 26

Dynamic Response Function Accelerations where What is this function? Why compute it? How do we compute it? Why is it hard to compute? Reaction Forces Control Inputs Ambiguity Variables System State Relates instantaneous behavior to controls and ambiguity for a particular To select control inputs which achieve desired instantaneous behavior By solving a series of linear systems of equalities and inequalities consisting of: 1) Lagrange’s equation 2)Contact constraints Non-linearity, Solution Ambiguity, Inconsistency, Inequality Constraints Slide 5 / 26

Related Research Single Rigid Bodies Ambiguities with Rigid Object, Two Walls. (Rajan, Burridge, Schwartz 1987) Configuration Space Friction Cone. (Erdmann 1994) Graphical Methods. (Mason 2001) Multi-Rigid-Bodies: Modeling and Simulation Early Application of LCP. (Lostedt 1982) Lagrangian dynamics and Corner Characteristic. (Pfeiffer and Glocker 1996) 3 D Case, Existence and Uniqueness Extensions. (Trinkle et al. 1997) Framework for dynamics with shocks (J. J. Moreau 1988) Early Application of Time Sweeping. (Monteiro Marques 1993) Formulation Guarentees Existence. (Anitescu and Potra 1997) Review of Current Work. (Stewart 2000) Multi-Rigid-Bodies: Control Computing Wrench Cones. (Balkcom and Trinkle 2002) (MPCC) Mathematical Program with Complementarity Constraint. (Anitescu 2000) Application of MPCC to Multi-Robot Coordination. (Peng, Anitescu, Akella 2003) Stability, Controllability, of Manipulation Systems. (Prattichizzo and Bicchi 1998) Open Questions for Control of Complementary Systems. (Brogliato 2003) Slide 6 / 26

Dynamics Equations (Pfeiffer and Glocker) Two coordinate systems (1) Generalized Coordinates (2) Contact Coordinates Related by Dynamic Equations on Generalized Coordinates: Joint Actuations Reaction Forces Slide 7 / 26

Contact Force Constraints Key Points on Contact Model (1) Reaction Forces are NOT an explicit function of state (2) Reaction Forces ARE constrained by state, acceleration Normal Force-Acceleration (Rigid Body) Tangential Force: Acceleration (Coulomb Friction) Contact Point (Pictures adapted from Pfeiffer, Glocker 1996) Slide 8 / 26

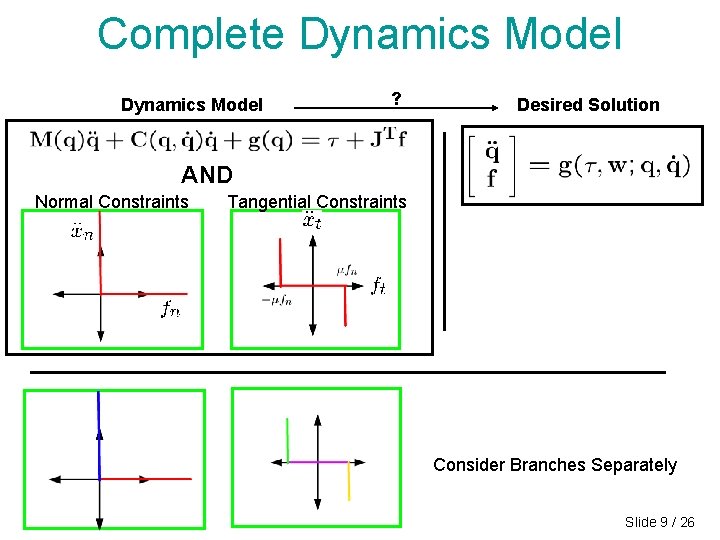
Complete Dynamics Model ? Desired Solution AND Normal Constraints Tangential Constraints Consider Branches Separately Slide 9 / 26

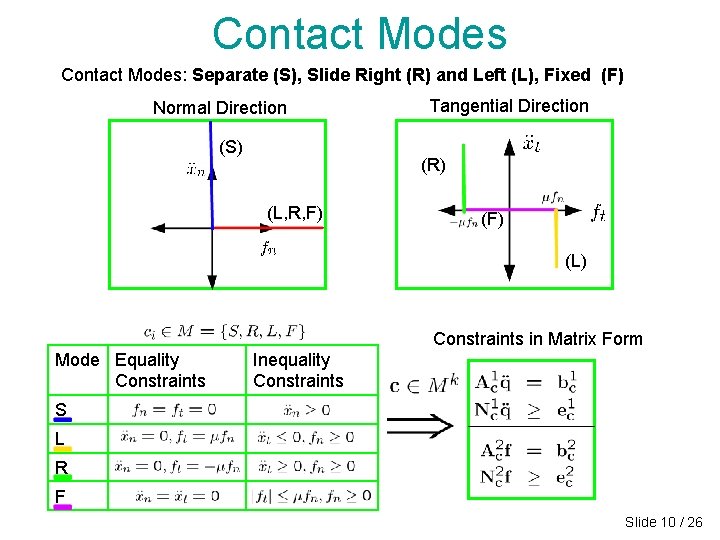
Contact Modes: Separate (S), Slide Right (R) and Left (L), Fixed (F) Normal Direction (S) Tangential Direction (R) (L, R, F) (L) Constraints in Matrix Form Mode Equality Constraints Inequality Constraints S L R F Slide 10 / 26

Form of Dynamic Response Contact Mode Specific Dynamics Model Contact Mode Solution AND Form of Total Solution ● Linear function ● Polytope domain from equality constraints from inequality constraints Slide 11 / 26

Solving for Response Function Consider equality constraints only ● Contact Mode Acceleration Constraints ● Contact Mode Force Constraints ● Dynamical Constraints (Group terms) Solve constraints based on rank- 4 cases is f. r. r. and f. c. r is f. r. r. but not f. c. r. Slide 12 / 26

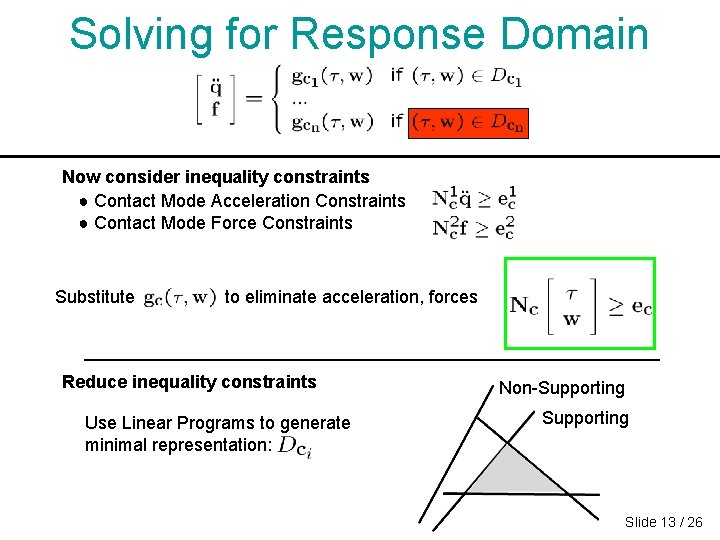
Solving for Response Domain Now consider inequality constraints ● Contact Mode Acceleration Constraints ● Contact Mode Force Constraints Substitute to eliminate acceleration, forces Reduce inequality constraints Use Linear Programs to generate minimal representation: Non-Supporting Slide 13 / 26

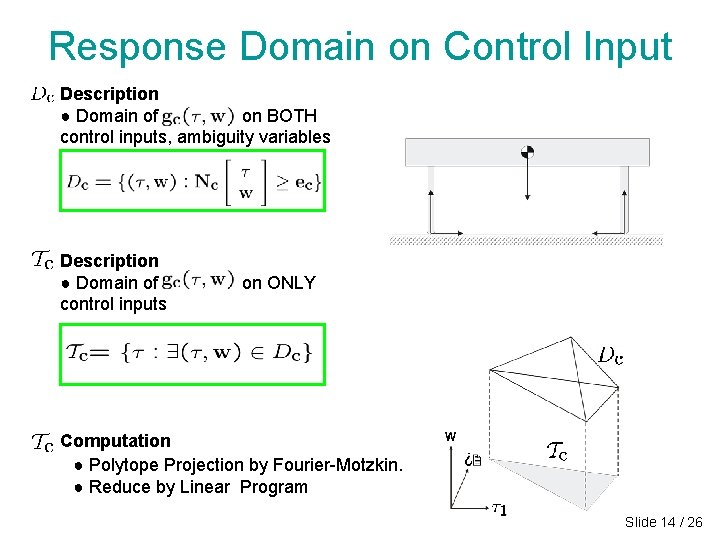
Response Domain on Control Input Description ● Domain of on BOTH control inputs, ambiguity variables Description ● Domain of control inputs on ONLY Computation ● Polytope Projection by Fourier-Motzkin. ● Reduce by Linear Program Slide 14 / 26

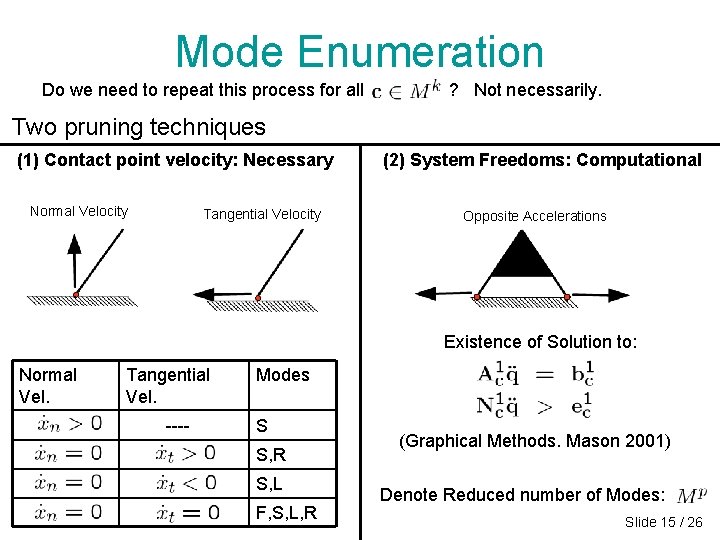
Mode Enumeration Do we need to repeat this process for all ? Not necessarily. Two pruning techniques (1) Contact point velocity: Necessary Normal Velocity Tangential Velocity (2) System Freedoms: Computational Opposite Accelerations Existence of Solution to: Normal Vel. Tangential Vel. ---- Modes S S, R S, L F, S, L, R (Graphical Methods. Mason 2001) Denote Reduced number of Modes: Slide 15 / 26

Algorithm Summary Goal: Characterize system dynamics as a function of control input Approach: Break up by contact mode, solve each mode Algorithm Steps: (1) Computed Mode Response (2) Computed Mode Response Domain (3) Computed Modes we need to consider Slide 16 / 26

Solution Ambiguity Definition: Multiple solutions exist for a particular Two Ambiguity Types: (Pfeiffer, Glocker 1996) (1) Between Modes (2) Within Mode Multiple Domains contain same Single Function has Slide 17 / 26

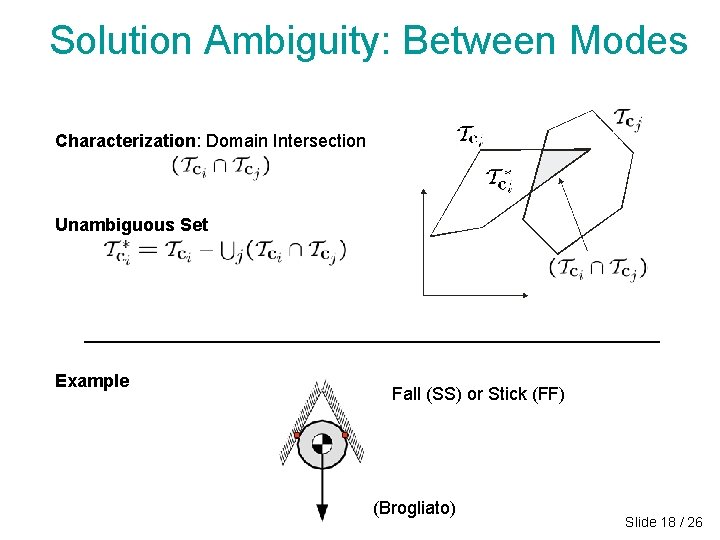
Solution Ambiguity: Between Modes Characterization: Domain Intersection Unambiguous Set Example Fall (SS) or Stick (FF) (Brogliato) Slide 18 / 26

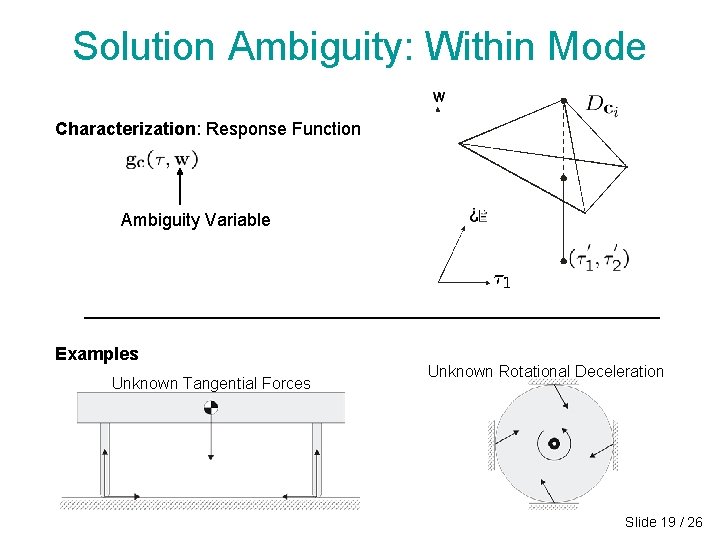
Solution Ambiguity: Within Mode Characterization: Response Function Ambiguity Variable Examples Unknown Tangential Forces Unknown Rotational Deceleration Slide 19 / 26

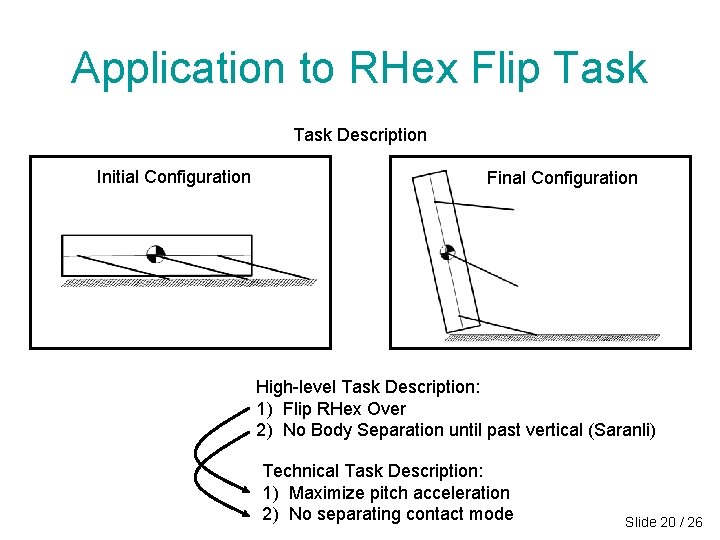
Application to RHex Flip Task Description Initial Configuration Final Configuration High-level Task Description: 1) Flip RHex Over 2) No Body Separation until past vertical (Saranli) Technical Task Description: 1) Maximize pitch acceleration 2) No separating contact mode Slide 20 / 26

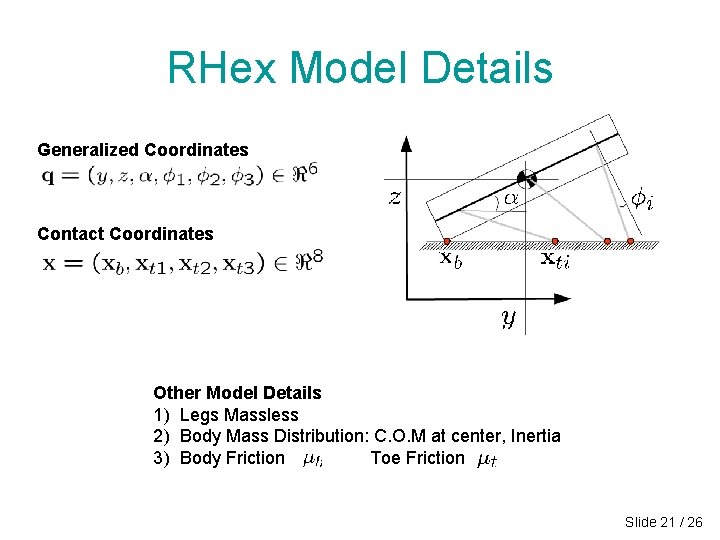
RHex Model Details Generalized Coordinates Contact Coordinates Other Model Details 1) Legs Massless 2) Body Mass Distribution: C. O. M at center, Inertia 3) Body Friction Toe Friction Slide 21 / 26

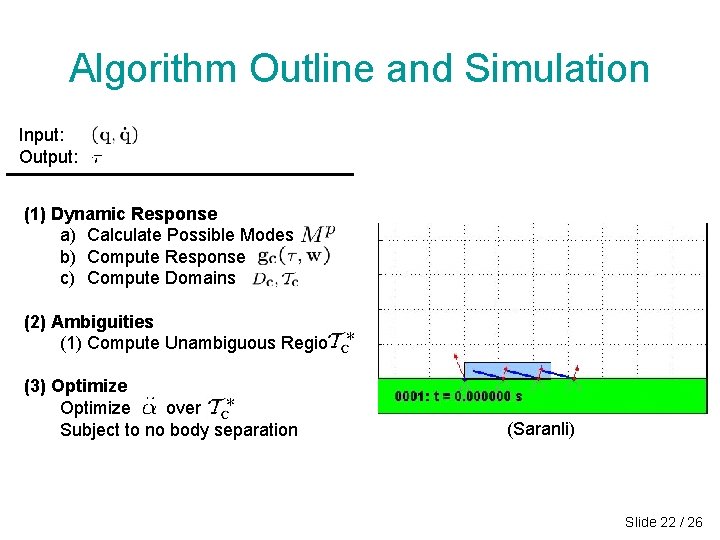
Algorithm Outline and Simulation Input: Output: (1) Dynamic Response a) Calculate Possible Modes b) Compute Response c) Compute Domains (2) Ambiguities (1) Compute Unambiguous Regions (3) Optimize over Subject to no body separation (Saranli) Slide 22 / 26

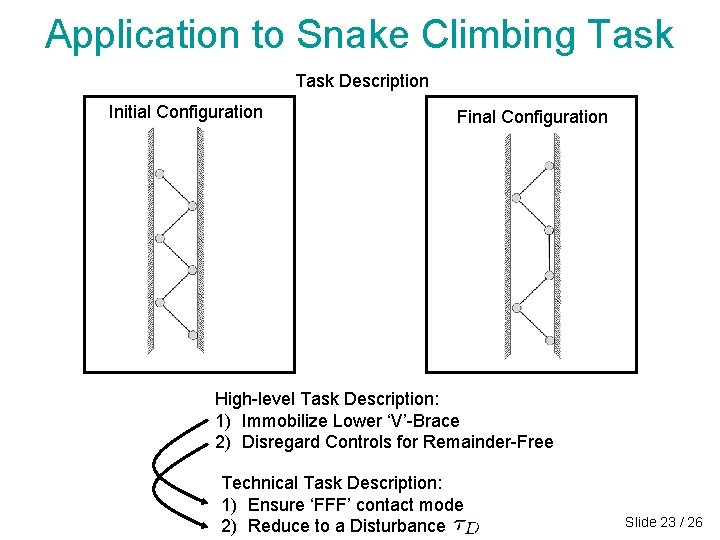
Application to Snake Climbing Task Description Initial Configuration Final Configuration High-level Task Description: 1) Immobilize Lower ‘V’-Brace 2) Disregard Controls for Remainder-Free Technical Task Description: 1) Ensure ‘FFF’ contact mode 2) Reduce to a Disturbance Slide 23 / 26

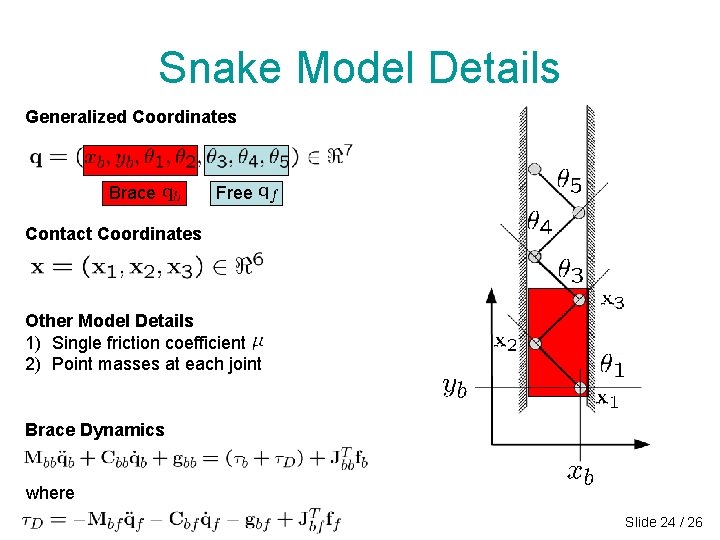
Snake Model Details Generalized Coordinates Brace Free Contact Coordinates Other Model Details 1) Single friction coefficient 2) Point masses at each joint Brace Dynamics where Slide 24 / 26

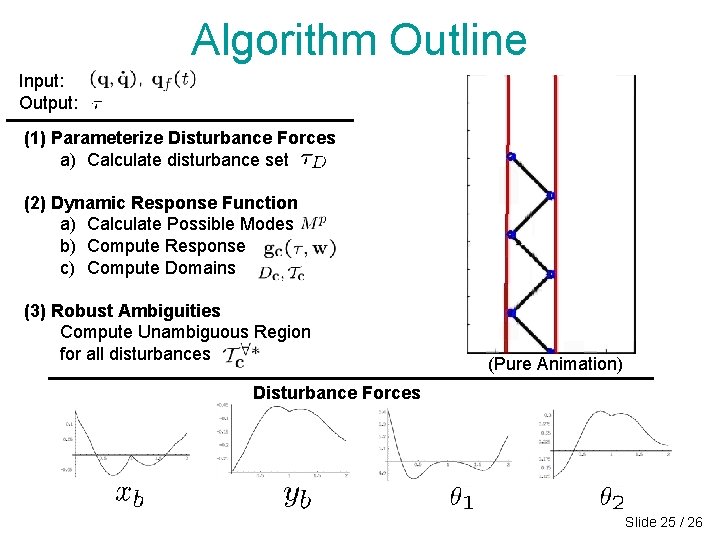
Algorithm Outline Input: Output: (1) Parameterize Disturbance Forces a) Calculate disturbance set (2) Dynamic Response Function a) Calculate Possible Modes b) Compute Response c) Compute Domains (3) Robust Ambiguities Compute Unambiguous Region for all disturbances (Pure Animation) Disturbance Forces Slide 25 / 26

Conclusion ● Objective: An approach to model-based control of frictionally constrained robots ● Dynamics Model: Multi-Rigid-Body with Coulomb Friction ● Model Prediction: Generate the dynamics response function ● Application: RHex flipping and Snake Climbing Slide 26 / 26

END TALK

Movie, Rhex Flip (Pure Animation) Slide 24 / 25

4 Cases is f. r. r. and f. c. r is not f. r. r. and f. c. r is f. r. r. but not f. c. r. is not f. r. r. and not f. c. r. when otherwise no solution