An application of binary trees Binary Expression Trees

An application of binary trees: Binary Expression Trees CS 308 Data Structures 1

A Binary Expression Tree is. . . A special kind of binary tree in which: 1. Each leaf node contains a single operand 2. Each nonleaf node contains a single binary operator 3. The left and right subtrees of an operator node represent subexpressions that must be evaluated before applying the operator at the root of the subtree. 2

Levels Indicate Precedence The levels of the nodes in the tree indicate their relative precedence of evaluation (we do not need parentheses to indicate precedence). Operations at higher levels of the tree are evaluated later than those below them. The operation at the root is always the last operation performed. 4

A Binary Expression Tree ‘*’ ‘+’ ‘ 4’ ‘ 3’ ‘ 2’ What value does it have? ( 4 + 2 ) * 3 = 18 5

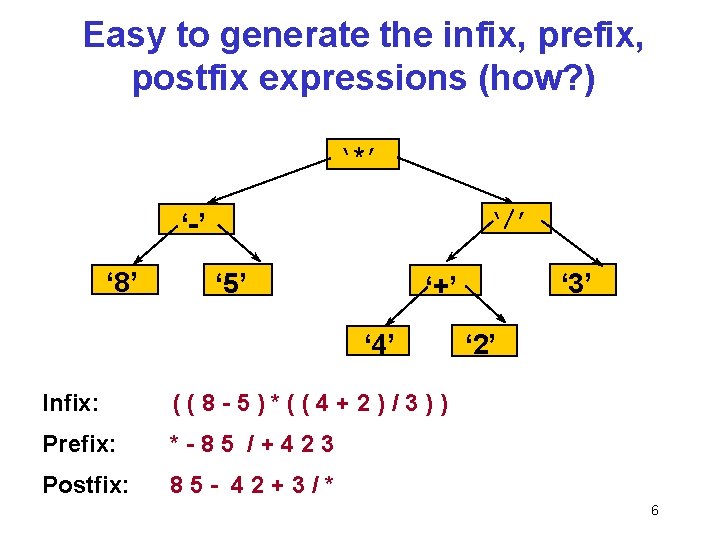
Easy to generate the infix, prefix, postfix expressions (how? ) ‘*’ ‘/’ ‘-’ ‘ 8’ ‘ 5’ ‘ 3’ ‘+’ ‘ 4’ Infix: ((8 -5)*((4+2)/3)) Prefix: *-85 /+423 Postfix: 85 - 42+3/* ‘ 2’ 6

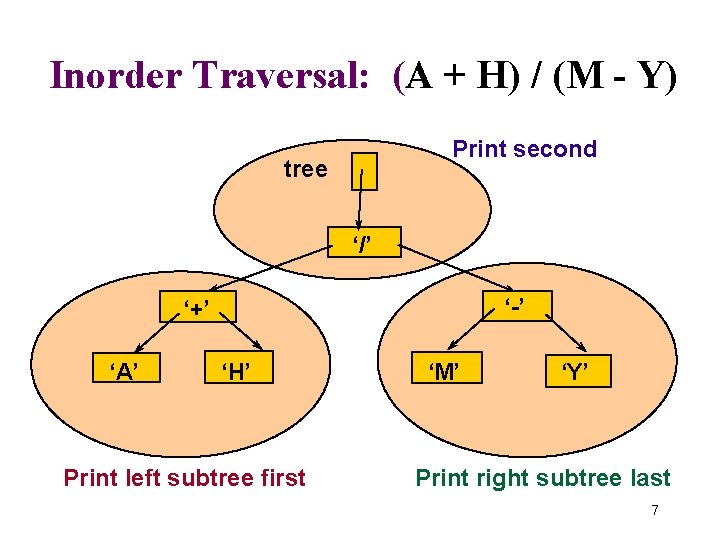
Inorder Traversal: (A + H) / (M - Y) Print second tree ‘/’ ‘-’ ‘+’ ‘A’ ‘H’ Print left subtree first ‘M’ ‘Y’ Print right subtree last 7

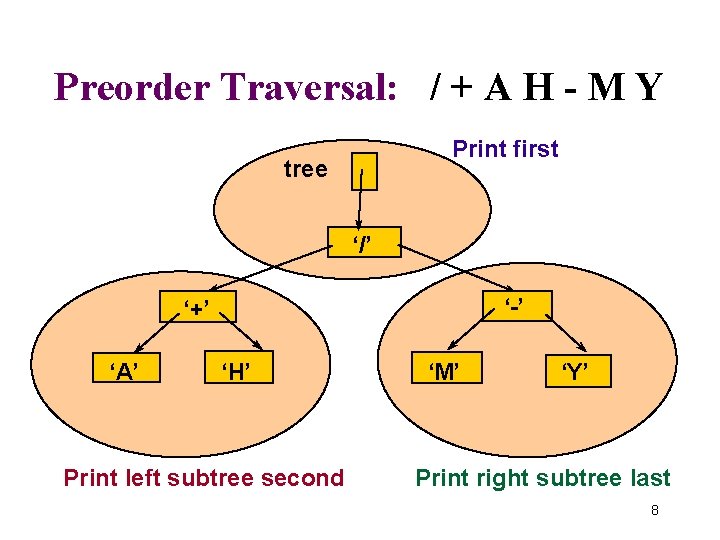
Preorder Traversal: / + A H - M Y Print first tree ‘/’ ‘-’ ‘+’ ‘A’ ‘H’ Print left subtree second ‘M’ ‘Y’ Print right subtree last 8

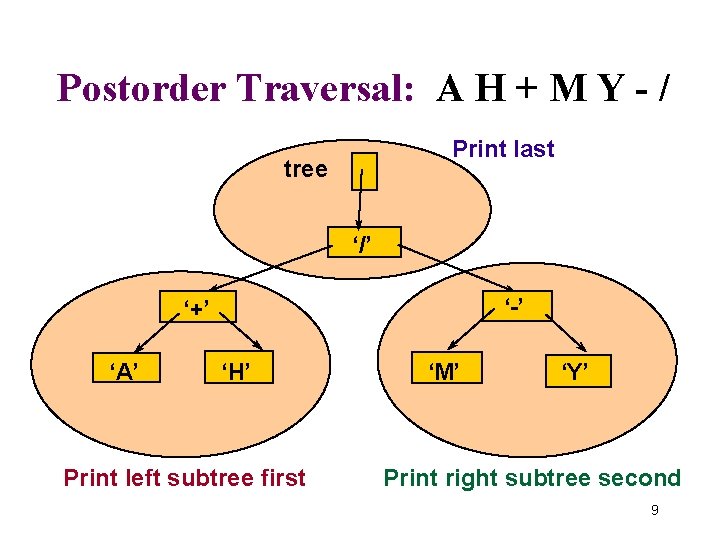
Postorder Traversal: A H + M Y - / Print last tree ‘/’ ‘-’ ‘+’ ‘A’ ‘H’ Print left subtree first ‘M’ ‘Y’ Print right subtree second 9

class Expr. Tree ~Expr. Tree Build Evaluate. . . ‘*’ private: Tree. Node* root; ‘+’ ‘ 4’ ‘ 3’ ‘ 2’ 10

Each node contains two pointers struct Tree. Node { Info. Node info ; Tree. Node* left ; Tree. Node* right ; }; NULL // Data member // Pointer to left child // Pointer to right child OPERAND. which. Type . left . info 7 6000 . operand . right 11

Info. Node has 2 forms enum Op. Type { OPERATOR, OPERAND } ; struct Info. Node { Op. Type union { char int } which. Type; // ANONYMOUS union operation ; operand ; }; OPERATOR. which. Type ‘+’. operation OPERAND. which. Type 7 . operand 12

int Eval ( Tree. Node* ptr ) { switch ( ptr->info. which. Type ) { case OPERAND : return ptr->info. operand ; case OPERATOR : switch ( tree->info. operation ) { case ‘+’ : return ( Eval ( ptr->left ) + Eval ( ptr->right ) ) ; case ‘-’ : return ( Eval ( ptr->left ) - Eval ( ptr->right ) ) ; case ‘*’ : return ( Eval ( ptr->left ) * Eval ( ptr->right ) ) ; case ‘/’ : return ( Eval ( ptr->left ) / Eval ( ptr->right ) ) ; } } } 13

Building a Binary Expression Tree from an expression in prefix notation l Insert new nodes, each time moving to the left until an operand has been inserted. l Backtrack to the last operator, and put the next node to its right. l Continue in the same pattern. 14