An appendageal model for the transport of hydrophilic

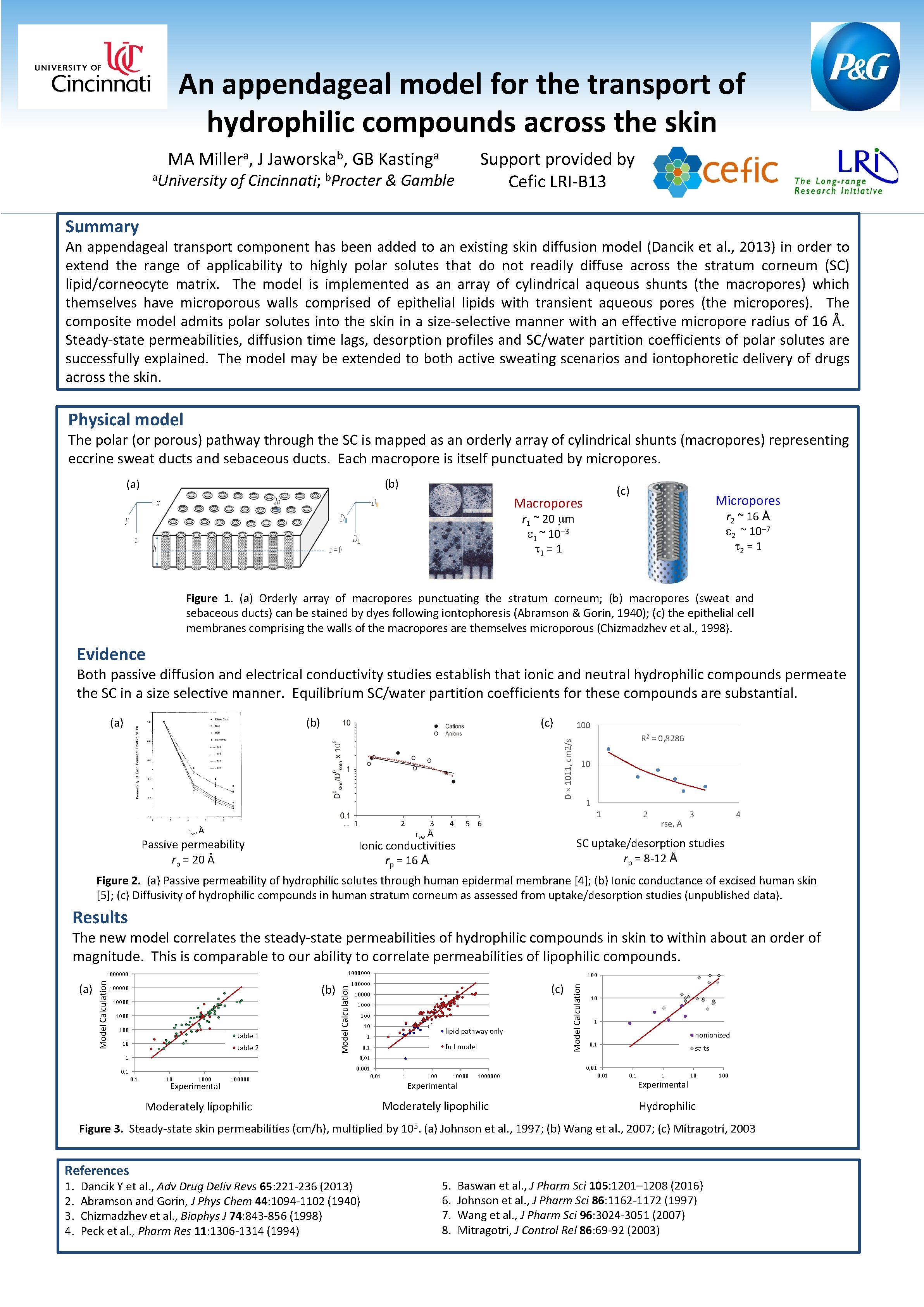
An appendageal model for the transport of hydrophilic compounds across the skin MA a Miller , a. University J b Jaworska , GB a Kasting Support provided by Cefic LRI-B 13 of Cincinnati; b. Procter & Gamble Summary An appendageal transport component has been added to an existing skin diffusion model (Dancik et al. , 2013) in order to extend the range of applicability to highly polar solutes that do not readily diffuse across the stratum corneum (SC) lipid/corneocyte matrix. The model is implemented as an array of cylindrical aqueous shunts (the macropores) which themselves have microporous walls comprised of epithelial lipids with transient aqueous pores (the micropores). The composite model admits polar solutes into the skin in a size-selective manner with an effective micropore radius of 16 Å. Steady-state permeabilities, diffusion time lags, desorption profiles and SC/water partition coefficients of polar solutes are successfully explained. The model may be extended to both active sweating scenarios and iontophoretic delivery of drugs across the skin. Physical model The polar (or porous) pathway through the SC is mapped as an orderly array of cylindrical shunts (macropores) representing eccrine sweat ducts and sebaceous ducts. Each macropore is itself punctuated by micropores. (b) (a) (c) Macropores Micropores r 2 ~ 16 Å 2 ~ 10 7 2 = 1 r 1 ~ 20 m 1 ~ 10 3 1 = 1 Figure 1. (a) Orderly array of macropores punctuating the stratum corneum; (b) macropores (sweat and sebaceous ducts) can be stained by dyes following iontophoresis (Abramson & Gorin, 1940); (c) the epithelial cell membranes comprising the walls of the macropores are themselves microporous (Chizmadzhev et al. , 1998). Evidence Both passive diffusion and electrical conductivity studies establish that ionic and neutral hydrophilic compounds permeate the SC in a size selective manner. Equilibrium SC/water partition coefficients for these compounds are substantial. (b) (c) 100 D × 1011, cm 2/s (a) 1 rse, Å Passive permeability rp = 20 Å 2 3 rse, Å 4 R 2 = 0, 8286 10 1 1 5 6 2 rse, Å 3 4 SC uptake/desorption studies rp = 8 -12 Å Ionic conductivities rp = 16 Å Figure 2. (a) Passive permeability of hydrophilic solutes through human epidermal membrane [4]; (b) Ionic conductance of excised human skin [5]; (c) Diffusivity of hydrophilic compounds in human stratum corneum as assessed from uptake/desorption studies (unpublished data). Results The new model correlates the steady-state permeabilities of hydrophilic compounds in skin to within about an order of magnitude. This is comparable to our ability to correlate permeabilities of lipophilic compounds. (b) 10000 100 table 1 10 table 2 1 100000 (c) 10000 100 10 lipid pathway only 1 full model 0, 1 Model Calculation (a) 100000 Model Calculation 1000000 10 1 nonionized 0, 1 salts 0, 01 0, 001 0, 1 10 1000 Experimental 100000 Moderately lipophilic 0, 01 1 10000 Experimental 1000000 Moderately lipophilic 0, 01 0, 1 1 Experimental 10 100 Hydrophilic Figure 3. Steady-state skin permeabilities (cm/h), multiplied by 105. (a) Johnson et al. , 1997; (b) Wang et al. , 2007; (c) Mitragotri, 2003 References 1. 2. 3. 4. Dancik Y et al. , Adv Drug Deliv Revs 65: 221 -236 (2013) Abramson and Gorin, J Phys Chem 44: 1094 -1102 (1940) Chizmadzhev et al. , Biophys J 74: 843 -856 (1998) Peck et al. , Pharm Res 11: 1306 -1314 (1994) 5. 6. 7. 8. Baswan et al. , J Pharm Sci 105: 1201– 1208 (2016) Johnson et al. , J Pharm Sci 86: 1162 -1172 (1997) Wang et al. , J Pharm Sci 96: 3024 -3051 (2007) Mitragotri, J Control Rel 86: 69 -92 (2003)