An annealing mutation operator in the genetic algorithms

An annealing mutation operator in the genetic algorithms for RNA folding Bruce A. Shapiro and Jin Chu Wu

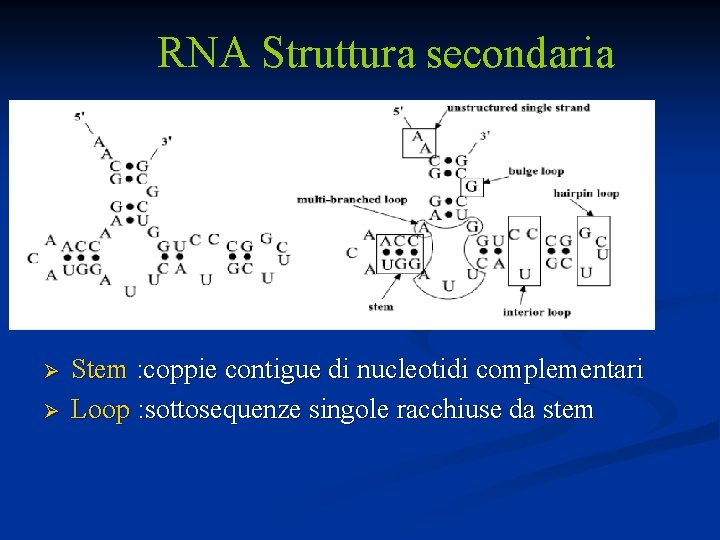
RNA Struttura secondaria Ø Ø Stem : coppie contigue di nucleotidi complementari Loop : sottosequenze singole racchiuse da stem

Struttura secondaria -l’RNA tende a “conservare” nel tempo la struttura secondaria più che la struttura primaria in se; è relativamente comune trovare esempi di RNA omologhi che hanno una struttura secondaria molto simile ma la cui sequenza non è simile per nulla. Cambiamenti drastici della sequenza sono quindi tollerati, purchè venga mantenuta la complementarietà delle basi accoppiate; -se ne deduce che l’evoluzione di una sequenza di RNA è vincolata dalla struttura. Questo rende l’analisi delle sequenze di RNA più difficile, rispetto all’analisi del DNA o delle proteine. Infatti, per la ricerca di RNA omologhi è necessario analizzare la similarità in termini di struttura secondaria conservata oltre che di sequenza.

Problema biologico L’obbiettivo primario è riuscire a trovare una struttura stabile e biologicamente funzionale La stabilità è data dall’energia di legame degli stem in maniera opposta i loop destabilizano la struttura per la repulsione delle basi non complementari

Algoritmo genetico Utilizzando una architettura parallela (mas par 2) con 16384 processori si è implementato un algoritmo genetico per la predizione del folding del RNA Che utilizza come parametro di fitness la energia libera procedendo attraverso 4 fasi Ø Preprocessing Ø Selezione Ø Mutazione Ø Crossing over

Preprocessing L’algoritmo Genera una popolazione iniziale di possibili stem dalla sequenza data

Selezione Ad ogni generazione ogni processore seleziona 2 sequenze da se stesso e dai suoi 8 processori vicini usando come parametro di selezione l’energia libera

Mutazione Delle 2 sequenze selezionate, l’algoritmo genera delle mutazioni nelle strutture selezionando stem random in accordo con l’operatore di mutazione dalle sequenze generate inizialmente formando 2 strutture figlie

Crossing over Ultimo passo di ogni iterazione è una funzione di incrocio tra strutture padre e strutture figlie eliminando eventuali interazioni terziarie Da queste due nuove strutture il G. A. sceglie la struttura che ha l’energia libera minore cosi da diventare la struttura della generazione successiva Ottenendo ad ogni iterazione un totale di 16384 nuove strutture in parallelo

Problema computazionale L’algoritmo genetico cosi come progettato non riesce a raggiungere risultati significativi anche dopo migliaia di generazioni in quanto genera molte strutture diverse fra loro specialmente per lunghe sequenze

Problema computazionale Soluzione: si cerca d’implementare un nuovo operatore di mutazione in quanto il vecchio operatore permette poche mutazioni all’inizio del processo aumentandole linearmente al crescere della dimensione della struttura secondaria, rendendo difficile la convergenza delle strutture

Operatore di mutazione Il numero di mutazioni in tutti i processori ad ogni generazione è dato da: N = numero totale di mutazioni ad ogni generazione S = grandezza media della struttura 2° P = probabilità di mutazione N = (16000*s*p)

Vecchio operatore Nel vecchio operatore di mutazione il parametro “p” veniva mantenuto costante cosi che il numero di mutazioni totali ad ogni generazione dipendeva da “s” permetteva poche mutazioni all’inizio del processo e incrementava il numero totale di mutazioni ad ogni generazione al crescere della dimensione della struttura secondaria Ottenendo come risultato per lunghe sequenze strutture secondarie molto diverse fra di loro anche dopo molte generazioni

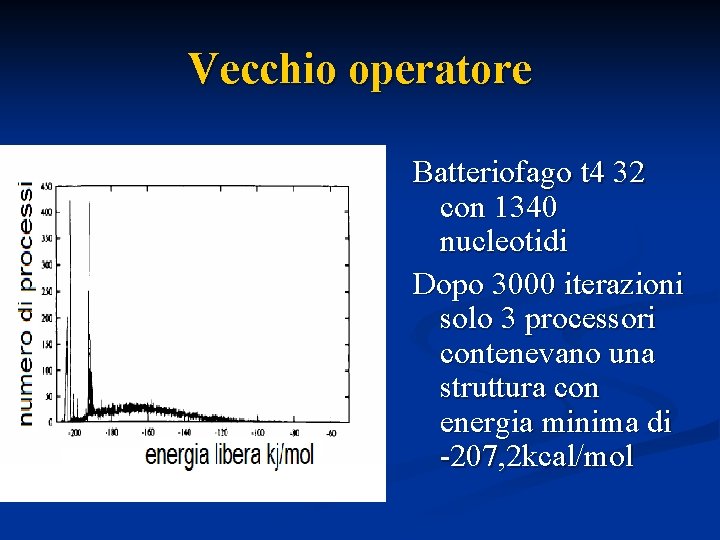
Vecchio operatore Batteriofago t 4 32 con 1340 nucleotidi Dopo 3000 iterazioni solo 3 processori contenevano una struttura con energia minima di -207, 2 kcal/mol

Nuovo operatore Il nuovo operatore si comporta in modo opposto al vecchio, permettendo un largo numero di mutazioni su tutti i processori all’inizio del processo per poi ridurle ad ogni generazione all’aumentare della dimensione della struttura secondaria Facendolo dipendere quindi dallo stem pool iniziale generato dalla fase di inizializzazione e dalla dimensione della struttura secondaria ad ogni generazione

Nuovo operatore La probabilità di mutazione “p” è stata progettata per discendere lungo una curva iperbolica al crescere della struttura secondaria secondo la relazione S 1= 1 stem all’inizio del processo p =(α/s)+β α = P 1 -s 1 β S 1<S 2 e P 1>P 2 P 1= dipende dalla popolazione iniziale generata dalla sequenza β = P 1 -P 2/s 1 -s 2 P = rapporto tra numero totale di mutazioni fratto i processori totali P = N/16000 P=s*p

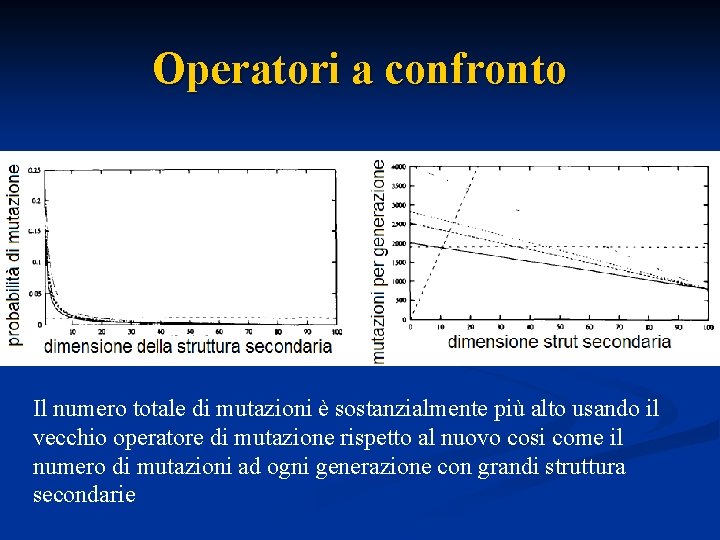
Operatori a confronto Il numero totale di mutazioni è sostanzialmente più alto usando il vecchio operatore di mutazione rispetto al nuovo cosi come il numero di mutazioni ad ogni generazione con grandi struttura secondarie

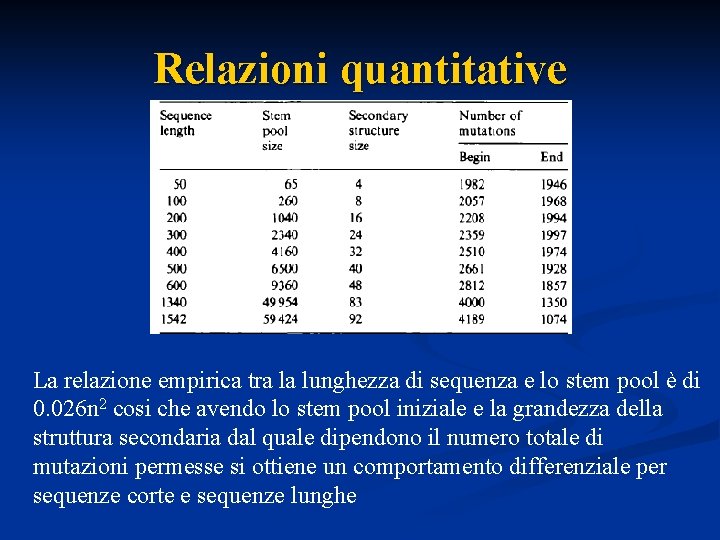
Relazioni quantitative La relazione empirica tra la lunghezza di sequenza e lo stem pool è di 0. 026 n 2 cosi che avendo lo stem pool iniziale e la grandezza della struttura secondaria dal quale dipendono il numero totale di mutazioni permesse si ottiene un comportamento differenziale per sequenze corte e sequenze lunghe

Terminazione Per una rapida convergenza su lunghe sequenze è stato implementato un criterio di terminazione basato su metodi statistici che usa come indice la distribuzione dell’energia libera su tutti i processori viene presa in considerazione l’energia il cui rapporto fra i processori che la posseggono fratto il totale dei processori supera una certa soglia fissata

Terminazione Da questa energia ottenuta si calcola la media ponderata usata poi per il calcolo dell’errore relativo ottenuto dal rapporto tra la deviazione standard fratto il valore assoluto della media ponderata cosi che ad ogni generazione la media dell’energia diventerà stabile Il programma termina quando l’errore relativo diviene minore d’un valore di incertezza empiricamente fissato come 10 -4

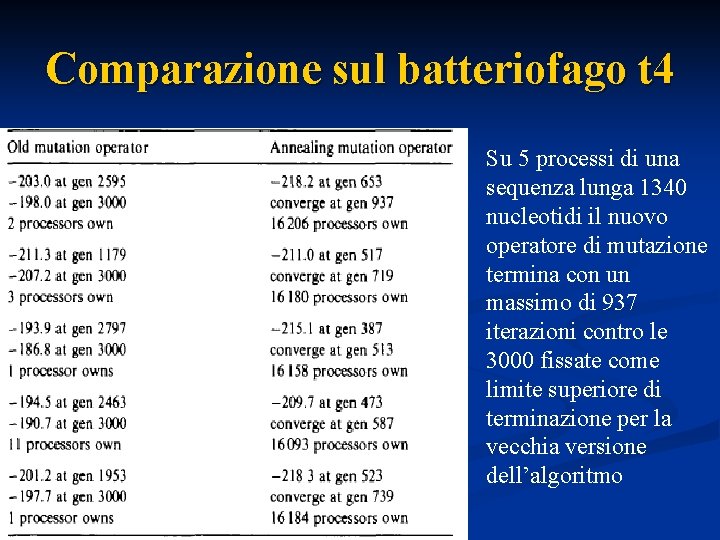
Comparazione sul batteriofago t 4 Su 5 processi di una sequenza lunga 1340 nucleotidi il nuovo operatore di mutazione termina con un massimo di 937 iterazioni contro le 3000 fissate come limite superiore di terminazione per la vecchia versione dell’algoritmo

Comparazione sul 16 s Con una sequenza di 1542 nucleotidi il numero di generazioni decresce

Struttura del 16 s Dalla struttura pubblicata il 16 s conta 4 domini e 1542 nucleotidi, 98 stem totali che coinvolgono 448 coppie di basi Ø 1° con 40 stem 1 -560 Ø 2° con 20 stem 561 -920 Ø 3° con 31 stem 921 -1400 Ø 4° con 7 stem 1401 -1542 Tra gli stem si conta uno psedoknots

Algoritmi a confronto I risultati del algoritmo genetico con il vecchio e nuovo operatore e un algoritmo deterministico DPA(dinamic programming algorithm Zuker e Stiegler 1989) che da un risultato univoco, vengono messi a confronto con la struttura pubblicata Ottenendo un energia libera dal G. A. di -359. 9 kcal/mol Mentre il risultato del DPA è di -443. 4 kcal/mol La struttura pubblicata ha un energia libera di -307. 4 kcal/mol

Algoritmi a confronto Nel trattare i risultati si devono eliminare gli stem che non sono considerati dagli algoritmi come quelli formati da una sola coppia di basi o gli pseudoknots Ø G. A. con il nuovo operatore ha il 28% di 93 stem Ø G. A. con il vecchio operatore ha il 25% di 93 stem Ø DPA non trovando singole coppie e pseudoknots ha una percentuale del 20 %

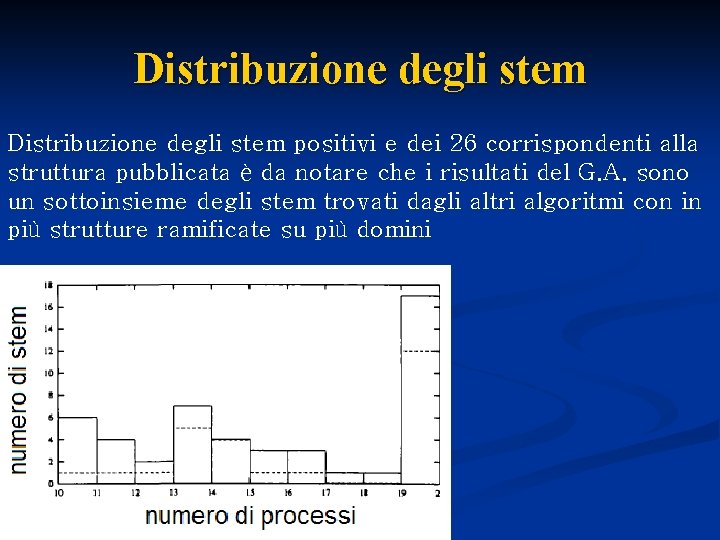
Distribuzione degli stem positivi e dei 26 corrispondenti alla struttura pubblicata è da notare che i risultati del G. A. sono un sottoinsieme degli stem trovati dagli altri algoritmi con in più strutture ramificate su più domini

Risultati e discussioni L’algoritmo genetico con il nuovo operatore di annealing migliora le prestazioni in termini di tempo d’esecuzione e convergenza migliorando anche la predizione in termini di struttura secondaria

Ulteriori variazioni Si prova a variare il numero di mutazioni ad ogni generazione rispetto alla dimensione della struttura secondaria non più con una relazione lineare come descritto precedentemente ma utilizzando funzioni che descrivono parabole concave e convesse su strutture con diversa dimensione Ø 26 sequenze corte Ø batteriofago T 4 Ø 16 s

Risultati Comparando i risultati per il 16 s non si sono riscontrate differenze sostanziali differentemente dal T 4 e le sequenze corte predette meglio dalla curva concava

Work in progress Il lavoro si focalizza verso una precisa correlazione tra la lunghezza di sequenza, la dimensione delle strutture generate inizialmente nella fase di preprocessing e la dimensione della struttura secondaria cosi da relazionarle con una nuova funzione che descrive la probabilità di mutazione