An Analysis of Packet Sampling in the Frequency

An Analysis of Packet Sampling in the Frequency Domain Luigi Alfredo Grieco (Politecnico di Bari, Italy) Chadi Barakat (INRIA, France) ACM IMC (Internet Measurement Conference) 2009 2010/3/19 Speaker: Li-Ming Chen

Motivation n Packet sampling, q q q n A technique to reduce the complexity of network monitoring system (by capturing a subset of packets) However, sampling introduces estimation errors Many papers have studied the problem with statistic tools In this paper, the authors look at packet sampling from another interesting perspective q q 2010/3/19 How does sampling impact the spectrum of the traffic? Try to evaluate the parts of the spectrum that get altered because of sampling and identify efficient non-biased inversion methods Speaker: Li-Ming Chen 2

Outline n n Background Problem Formulation q q n n n P = 1, No sampling P < 1, Sampling Aliasing Noise Elimination Evaluation Conclusion 2010/3/19 Speaker: Li-Ming Chen 3

Background: Fourier Transform (FT) n FT describes which frequencies are present in the original function q Given a signal/function x(t) in time domain, FT measure the magnitude of the frequency f in frequency domain by computing: basic building block: complex exp. are periodic functions of t under different input freq. f when f=3, X(f) has max. Original function x(t) = FT f=5, X(f)->0 Appears to oscillate at 3 cycles/sec. 2010/3/19 Time (s) Speaker: Li-Ming Chen Freq. (Hz) 3 5 4

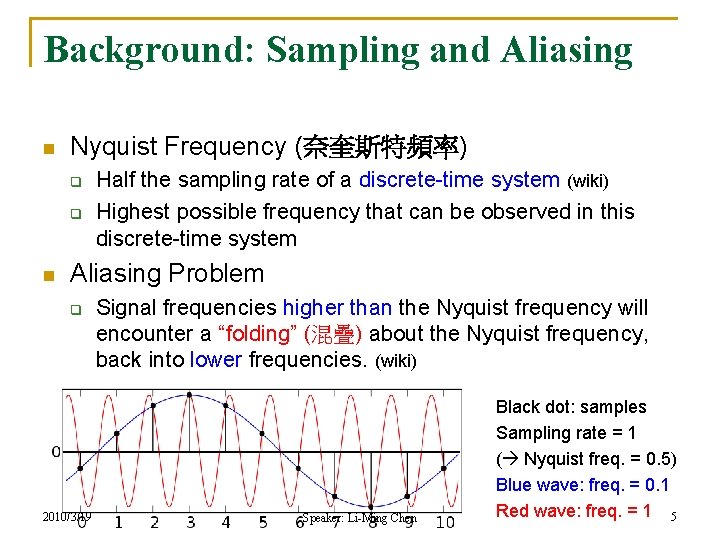
Background: Sampling and Aliasing n Nyquist Frequency (奈奎斯特頻率) q q n Half the sampling rate of a discrete-time system (wiki) Highest possible frequency that can be observed in this discrete-time system Aliasing Problem q 2010/3/19 Signal frequencies higher than the Nyquist frequency will encounter a “folding” (混疊) about the Nyquist frequency, back into lower frequencies. (wiki) Speaker: Li-Ming Chen Black dot: samples Sampling rate = 1 ( Nyquist freq. = 0. 5) Blue wave: freq. = 0. 1 Red wave: freq. = 1 5

Demo 1: Aliasing Youtube: http: //www. youtube. com/watch? v=Ukot. Zy 3 l. Qqo (in case you don’t have Youtube plugin) 2010/3/19 Speaker: Li-Ming Chen 6

Demo 2: Aliasing Youtube: http: //www. youtube. com/watch? v=e. J 6 vad. FVj. Yg (in case you don’t have Youtube plugin) 2010/3/19 Speaker: Li-Ming Chen 7

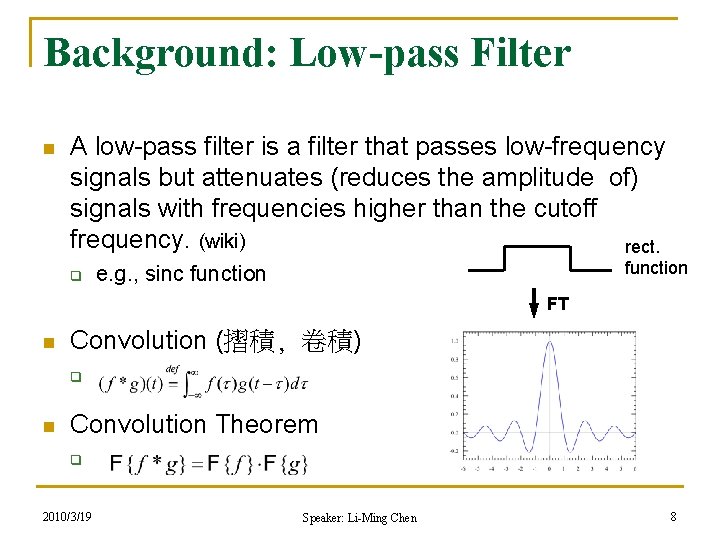
Background: Low-pass Filter n A low-pass filter is a filter that passes low-frequency signals but attenuates (reduces the amplitude of) signals with frequencies higher than the cutoff frequency. (wiki) rect. q function e. g. , sinc function FT n Convolution (摺積, 卷積) q n Convolution Theorem q 2010/3/19 Speaker: Li-Ming Chen 8

Outline n n Background Problem Formulation q q n n n P = 1, No sampling P < 1, Sampling Aliasing Noise Elimination Evaluation Conclusion 2010/3/19 Speaker: Li-Ming Chen 9

Problem Formulation bytes (per packet) bytes (per time unit) … S 4 T 3 T 2 T T 0 time bin, (traffic measurement) sampling p (random sampling) bytes (per packet) … S 2010/3/19 R bytes (per time unit) 4 T 3 T 2 T T 0 R Q: what happens after sampling? Speaker: Li-Mingin. Chen (especially the frequency domain…? ) 10

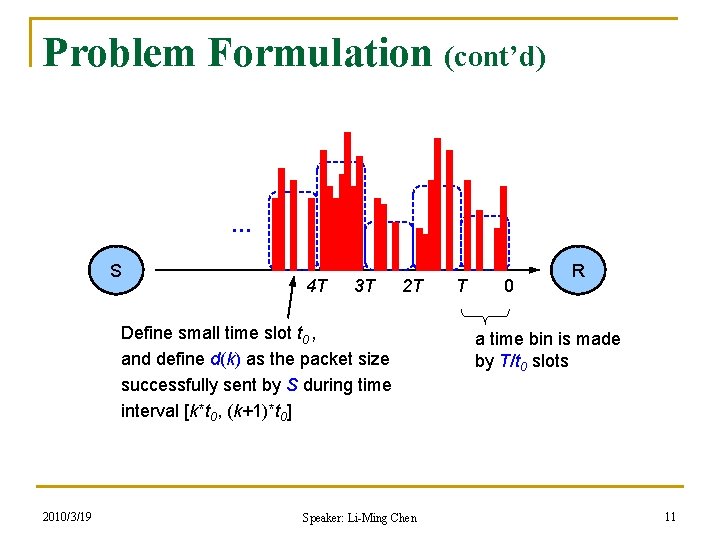
Problem Formulation (cont’d) … S 4 T 3 T 2 T Define small time slot t 0 , and define d(k) as the packet size successfully sent by S during time interval [k*t 0, (k+1)*t 0] 2010/3/19 Speaker: Li-Ming Chen T 0 R a time bin is made by T/t 0 slots 11

p = 1, Capturing All Packets • Fourier transform: D(f) = FT(d(k)) • E[D(f)] expected Fourier transform of d(k) A general form to represent a function with period 1/t 0. D 0(f) = 0, if |f| > 0. 5/t 0 2010/3/19 define f. M the. Chen max. freq. of D 0(f) Speaker: Li-Ming 12

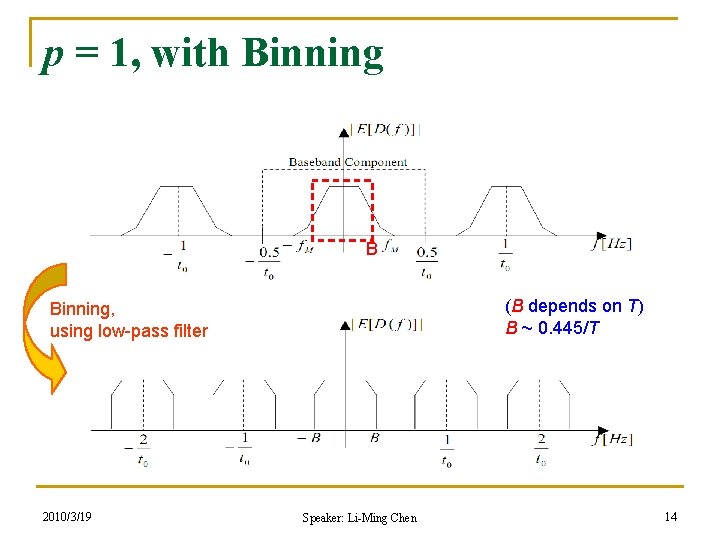
p = 1, with Binning n Usually, we measure traffic with time bins (T) q n This may affect the representation in the frequency domain Aggregated view: q Summing data received in a bin can be expressed as filtering d(k) using a discrete-time low-pass filter h(k) n q Do convolution, But in freq. domain, H(f) = FT(h(k)), a low-pass filter 2010/3/19 Speaker: Li-Ming Chen 13

p = 1, with Binning B (B depends on T) B ~ 0. 445/T Binning, using low-pass filter 2010/3/19 Speaker: Li-Ming Chen 14

p < 1, with Packet Sampling Q 1: after sampling, how this spectrum is related to the spectrum of the original traffic? Q 2: which part of the spectrum can be recovered without noise? n Main result: q For a traffic rate signal, estimation errors are fully avoided iff T – average interval; p – packet sampling rate; f. M – max. freq. in the baseband; q 2010/3/19 In other cases, the estimation errors are due to frequency aliasing effects that can not be filtered out. Speaker: Li-Ming Chen 15

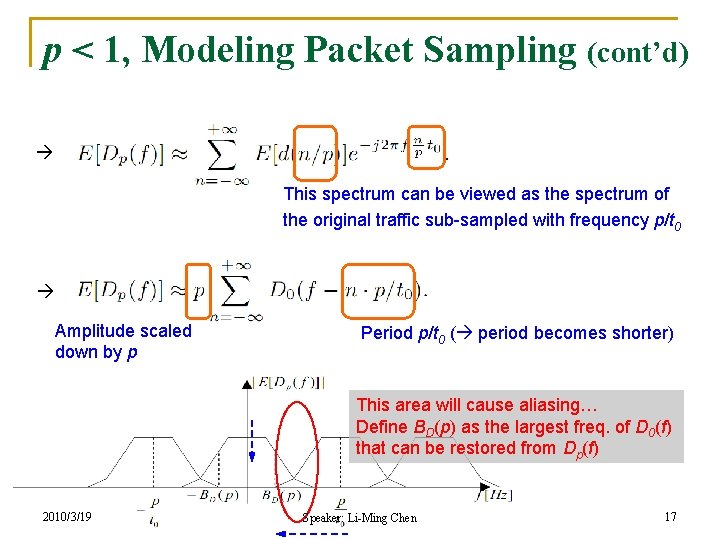
p < 1, Modeling Packet Sampling • After sampling: d(k) dp(k) • Denote the time slot corresponding to the n-th captured sample of d(k) as Δn is a r. v. modeling the time between sampled packets FT(dp(k)) = Focus on low-freq. components, 2010/3/19 Speaker: Li-Ming Chen 16

p < 1, Modeling Packet Sampling (cont’d) This spectrum can be viewed as the spectrum of the original traffic sub-sampled with frequency p/t 0 Amplitude scaled down by p Period p/t 0 ( period becomes shorter) This area will cause aliasing… Define BD(p) as the largest freq. of D 0(f) that can be restored from Dp(f) 2010/3/19 Speaker: Li-Ming Chen 17

p < 1, Why Binning!? n n Using low-pass filter to eliminate aliasing As mentioned, binning in the time domain is like multiplying a low-pass filter in the frequency domain Idea: q q Filter dp(k) using a low-pass filter with bandwidth B, then correct estimation could be achieved if in real cases, f. M could be very close to 0. 5/t 0 n Besides, the signal dp(k) should be divided by p q 2010/3/19 In order to compensate the scaling due to sampling Speaker: Li-Ming Chen 18

Summary n Packet sampling will cause estimation error after inversion process n Packet sampling will scale down the amplitudes and introduce aliasing problem in the frequency domain n “Binning” in the time domain could be viewed as applying lowpass filter in the frequency domain (and can avoid aliasing) n Next, the error in the estimation of the traffic volume is modeled as an aliasing effect in the frequency domain 2010/3/19 Speaker: Li-Ming Chen 19

Outline n n Background Problem Formulation q q n n n P = 1, No sampling P < 1, Sampling Aliasing Noise Elimination Evaluation Conclusion 2010/3/19 Speaker: Li-Ming Chen 20

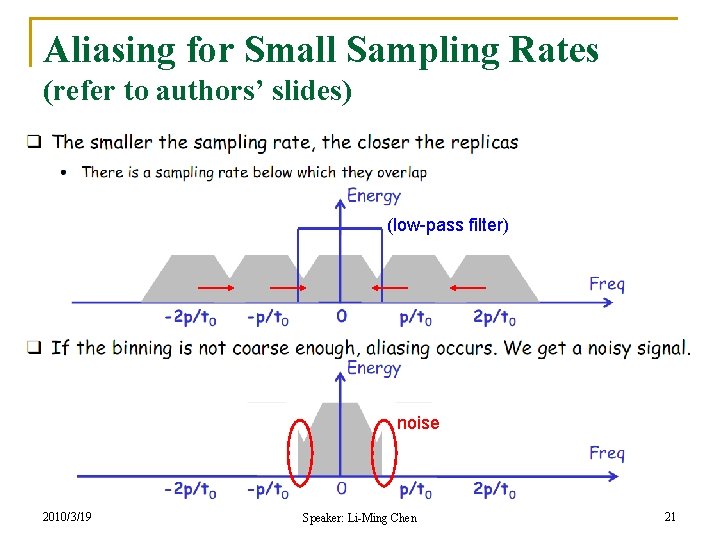
Aliasing for Small Sampling Rates (refer to authors’ slides) (low-pass filter) noise 2010/3/19 Speaker: Li-Ming Chen 21

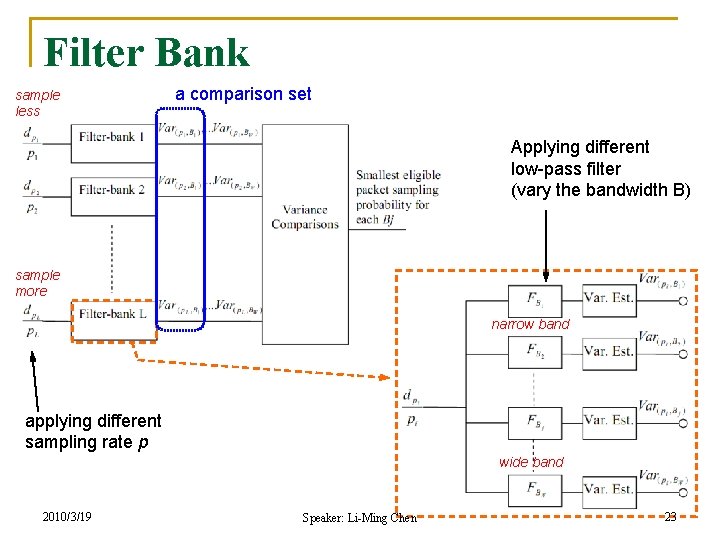
Aliasing Noise Elimination n Goal: q q n Observation: q n Identify suitable p and T for traffic measurement To know what portion of the spectrum of the network traffic can be restored once packet sampling has been applied Increasing p, not only the energy of the noise decreases but also its 1 st order derivative w. r. t. p decreases Solution: q q q 2010/3/19 Using “filter band” to check the variance of the energy of the spectrum If variance quickly increases, aliasing exists If variance slowly increases, the bin size is fine Speaker: Li-Ming Chen 22

Filter Bank sample less a comparison set Applying different low-pass filter (vary the bandwidth B) sample more narrow band applying different sampling rate p wide band 2010/3/19 Speaker: Li-Ming Chen 23

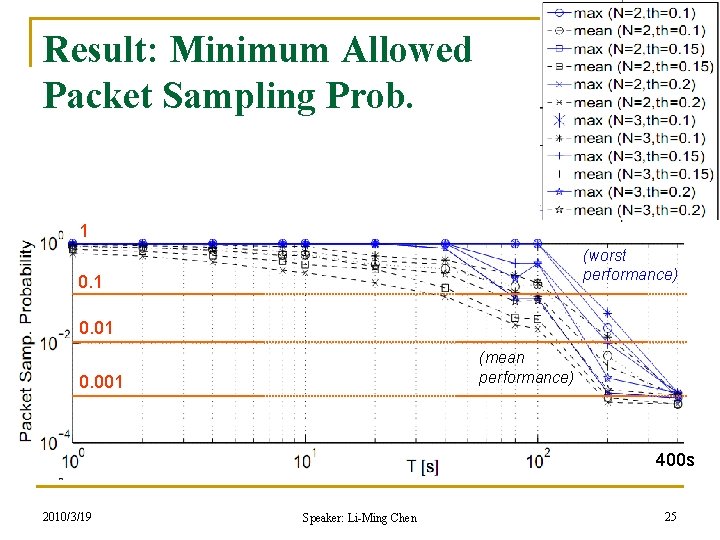
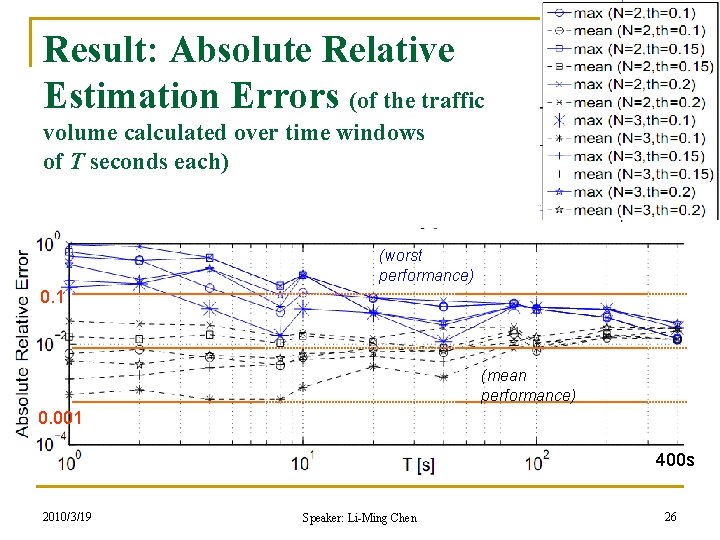
Experiments n n Using real traffic trace collected in Jan 2009 Given Bj and pi, q The algorithm compares the ratios (observe the deviation) q q 2010/3/19 w. r. t. a threshold th 0 = 1 + th the considered value of p = pi is admissible for the bandwidth Bj iff all the considered ratios are smaller than th 0! Speaker: Li-Ming Chen 24

Result: Minimum Allowed Packet Sampling Prob. 1 (worst performance) 0. 1 0. 01 (mean performance) 0. 001 400 s 2010/3/19 Speaker: Li-Ming Chen 25

Result: Absolute Relative Estimation Errors (of the traffic volume calculated over time windows of T seconds each) (worst performance) 0. 1 (mean performance) 0. 001 400 s 2010/3/19 Speaker: Li-Ming Chen 26

Conclusion n An analysis of packet sampling in the frequency domain q n n A novel technique to model the impact of noise caused be packet sampling A real-time algorithm is presented to detect the spectrum portion of the network traffic signal that can be restored once packet sampling has been applied. Future work: q 2010/3/19 Extend the proposed approach to large contexts as network -wide monitoring, application-level analysis and anomaly detection. Speaker: Li-Ming Chen 27

My Comments n Infocom’ 10 mini-conference: q q n n Interesting work, rely on statistical & signal processing methods Only focus on random sampling q n Compare to other “smart sampling techniques” !? Research: q n “A Frequency Domain Model to Predict the Estimation Accuracy of Packet Sampling” Exploit their finding to derive closed-form expressions for SNR Statistical skills, simplification skills Filter bank ~ brute force/exhaust search 2010/3/19 Speaker: Li-Ming Chen 28