An Analysis of BGP Convergence Properties Introduction The

An Analysis of BGP Convergence Properties • Introduction – The BGP protocol – NP completeness • Routing anomalies • Complexity analysis • Summery

Introduction (BGP( • Static BGPSolution: - the de-facto EGP. • Programs Policy-based Routing path-vector Policies protocol. Analysis – nlri, next-hop, as-path, loc-pref • The Route Arbiter Project • Implemented with little global knowledge. – Routing Policy Specification Language (RPSL. ( – Internetdivergence. Route Registries (IRRs. ( • Protocol –– Software (RATool. Set. ( Dynamic Tools solution. – Static solution.

Introduction (NP-Completeness( • • • Non Deterministic Turing Machine (NDTM. ( NP problems class. NP-Complete problems class. Reductions. A NP-Hard, A NP-Complete. The 3 -SAT problem: )x y z) (x y z(

Routing Anomalies The DISAGREE System • AS 1 prefers route 1 -2 -0. • AS 2 prefers route 2 -1 -0.
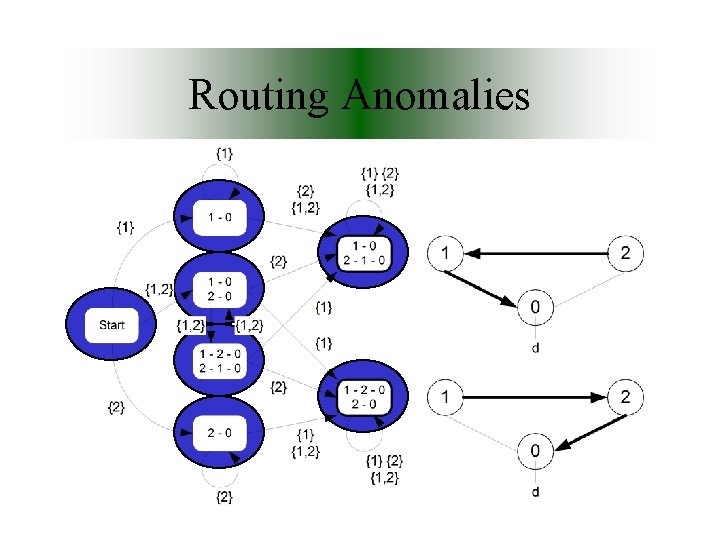
Routing Anomalies
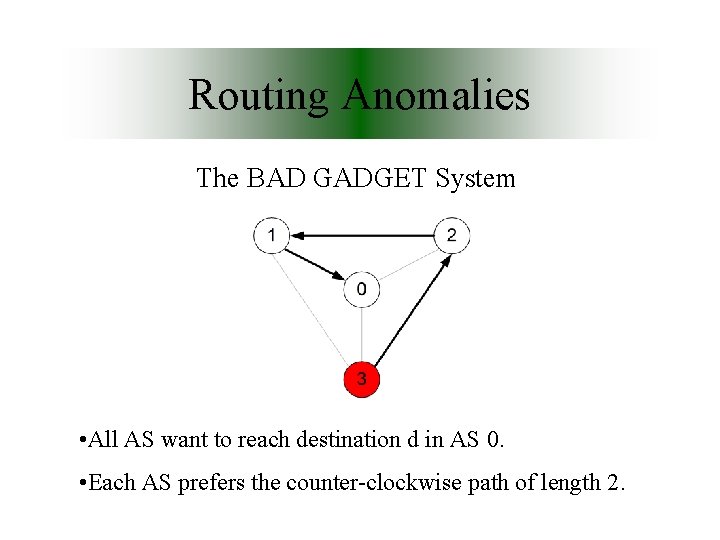
Routing Anomalies The BAD GADGET System • All AS want to reach destination d in AS 0. • Each AS prefers the counter-clockwise path of length 2.

Routing Anomalies The BAD GADGET System

Routing Anomalies The BAD GADGET System • All AS 2 export rules: – nlri = d loc-pref = 1 • AS 2 import(2<-1) rules: – )nlri = d as-path = [3, 0]) loc-pref = 2 – nlri = d loc-pref = 1 • AS 2 import(2<-3) rules: – nlri = d loc-pref = 1

Complexity Analysis The ASSIGN System An example of a 3 -SAT problem: )x y z) ( x y z(

Complexity Analysis The ASSIGN System X=True, Y=False, Z=False

Complexity Analysis REACHABILITY )single destination(
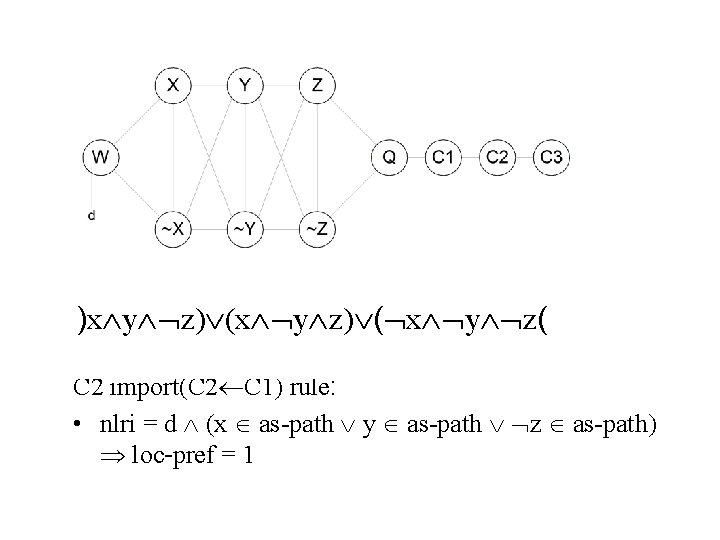
)x y z) ( x y z( C 2 import(C 2 C 1) rule: • nlri = d (x as-path y as-path z as-path) loc-pref = 1

Complexity Analysis ASYMMETRY

Complexity Analysis SOLVABILITY )single destination(

Complexity Analysis Relevant Routing Issues • • • REACHABILITY. ASYMMETRY. SOLVABILITY. TRAPPED. K-ROBUST. UNIQUE.

Summery Static Analysis approach problems: • Routing policies are not shared. • Complexity results need to rely on heuristics analysis rather than on exact analysis. A
- Slides: 16