An Algorithm for the Coalitional Manipulation Problem under

An Algorithm for the Coalitional Manipulation Problem under Maximin Michael Zuckerman, Omer Lev and Jeffrey S. Rosenschein AAMAS’ 11

Agenda n Introduction n Constructive Coalitional Unweighted Manipulation (CCUM) problem n Algorithm for CCUM under Maximin n 5/3 -approximation of the optimum n Lower bound on approximation ratio n Simulation results n Conclusions

Introduction n Elections n Voters submit linear orders of the candidates n A voting rule determines the winner based on the votes n Manipulation n A voter casts a vote that is not his true preference, to make himself better off n Gibbard-Satterthwaite theorem n Every reasonable voting rule is manipulable

Constructive Coalitional Unweighted Manipulation (CCUM) problem n Given n A voting rule r n The Profile of Non-Manipulators PNM n Candidate p preferred by the manipulators n Number of manipulators |M| n We are asked whether or not there exists a Profile of Manipulators PM such that p is the winner of PNM υ PM under r.

Unweighted Coalitional Optimization (UCO) problem n Given n A voting rule r n The Profile of Non-Manipulators PNM n Candidate p preferred by the manipulators n We are asked to find the minimum k such that there exists a set of manipulators M with |M| = k, and a Profile of Manipulators PM such that p is the winner of PNM υ PM under r.

Our setting, maximin n C = {c 1, …, cm} – the set of candidates n S, |S| = N – the set of N non-manipulators n T, |T| = n – the set of n manipulators n Ni(c, c’) = |{ k | c >k c’, >k S υ {1, …, i}}| – the number of voters from S and from the i first manipulators, which prefer c over c’ n Si(c) = minc’≠c. Ni(c, c’) – the maximin score of c from S and the i first manipulators n Maximin winner = argmaxc{Sn(c)} n Denote MINi(c) = {c’ C | Si(c) = Ni(c, c’)}

CCUM Complexity n CCUM under Maximin is NP-complete for any fixed number of manipulators (≥ 2) (Xia et al. ’ 09 [1]) n It follows that the UCO is not approximable by constant better than 3/2, unless P = NP Otherwise, if opt = 2, then the output of the algorithm would be < 3, i. e. , 2 n Hence, it would solve the CCUM for n = 2, a contradiction n

The heuristic / approximation algorithm n Fix some order on manipulators n The current manipulator i n n Ranks p first Builds a digraph Gi-1 = (V, Ei-1), where n V = C {p}; (x, y) § Ei-1 iff (y MINi-1(x) and p MINi-1(x)) Iterates over the candidates who have not yet been ranked § If there is a candidate with out-degree 0, then it adds such a candidate with the lowest score § Otherwise, adds a vertex with the lowest score § Removes all the outgoing edges of vertices who had outgoing edge to newly added vertex

Additions to the algorithm n The candidates with out-degree 0 are kept in stacks in order to guarantee a DFS-like order among the candidates with the same scores n If there is no candidate (vertex) with outdegree 0, then it first searches for a cycle, with 2 adjacent vertices having the lowest scores n If it finds such a pair of vertices, it adds the front vertex

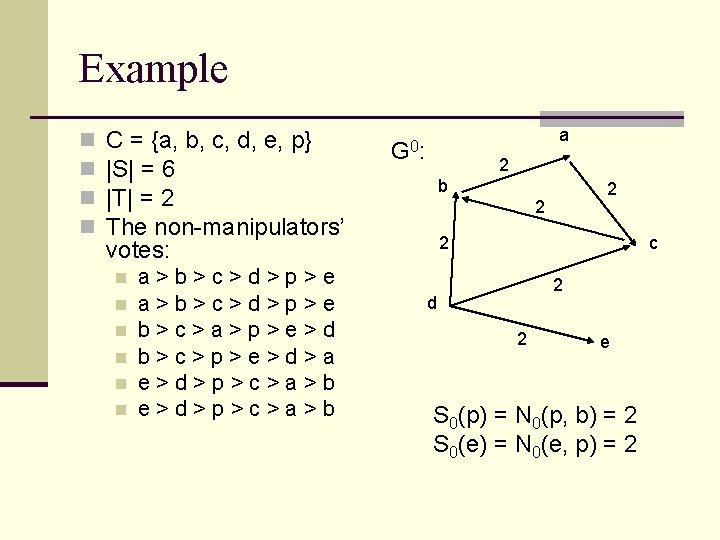
Example n n C = {a, b, c, d, e, p} |S| = 6 |T| = 2 The non-manipulators’ votes: n n n a>b>c>d>p>e b>c>a>p>e>d b>c>p>e>d>a e>d>p>c>a>b a G 0: 2 b 2 2 2 c 2 d 2 e S 0(p) = N 0(p, b) = 2 S 0(e) = N 0(e, p) = 2

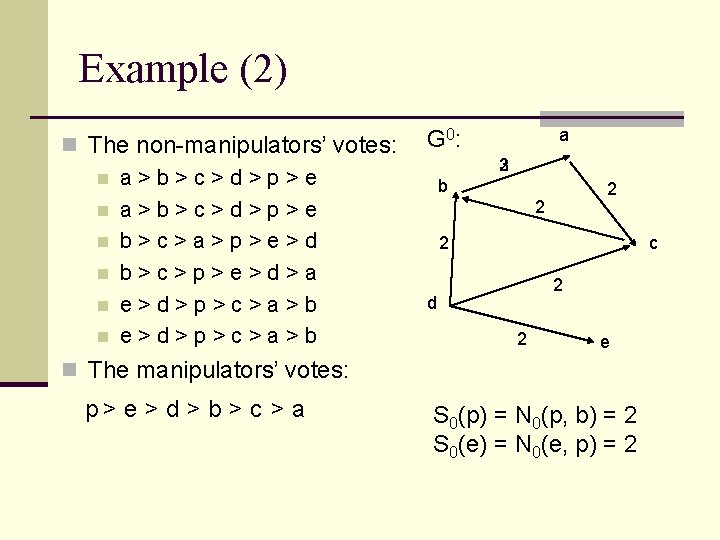
Example (2) n The non-manipulators’ votes: n a>b>c>d>p>e n b>c>a>p>e>d n b>c>p>e>d>a n e>d>p>c>a>b a G 0: 2 3 b 2 2 2 c 2 d 2 e n The manipulators’ votes: p> e > d > b > c > a S 0(p) = N 0(p, b) = 2 S 0(e) = N 0(e, p) = 2

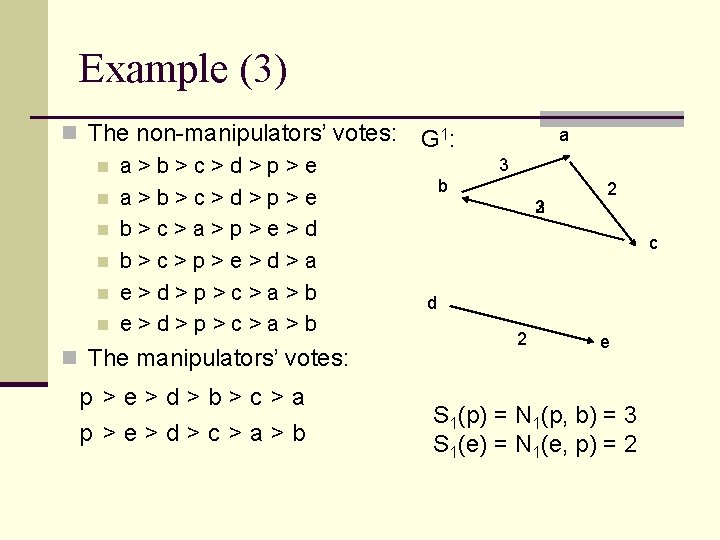
Example (3) n The non-manipulators’ votes: n a>b>c>d>p>e n b>c>a>p>e>d n b>c>p>e>d>a n e>d>p>c>a>b n The manipulators’ votes: p >e>d>b>c >a p >e>d>c >a>b a G 1: 3 b 2 3 2 c d 2 e S 1(p) = N 1(p, b) = 3 S 1(e) = N 1(e, p) = 2

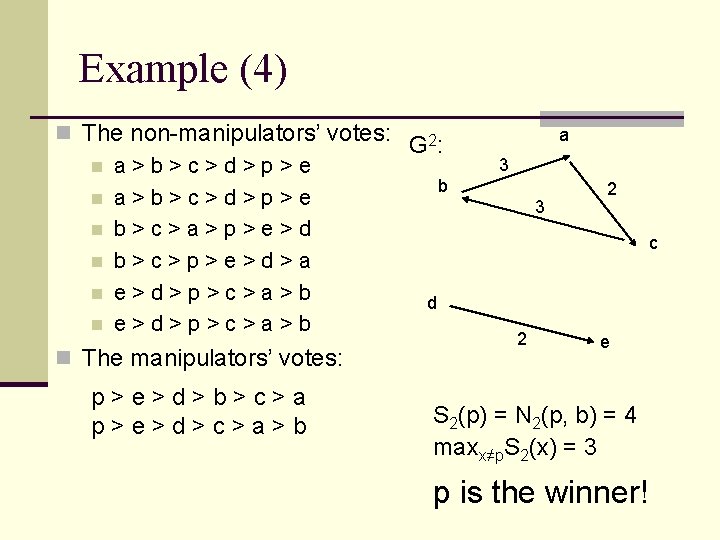
Example (4) n The non-manipulators’ votes: G 2: n a>b>c>d>p>e b n a>b>c>d>p>e n b>c>a>p>e>d n b>c>p>e>d>a n e>d>p>c>a>b d n e>d>p>c>a>b n The manipulators’ votes: p>e>d>b>c>a p>e>d>c>a>b a 3 3 2 c 2 e S 2(p) = N 2(p, b) = 4 maxx≠p. S 2(x) = 3 p is the winner!

Instances without 2 -cycles n Denote msi = maxc≠p. Si(c) n The maximum score of p’s opponents after i stages n Lemma: If there are no 2 -cycles in the graphs built by the algorithm, then for all i, 0 ≤ i ≤ n-3 it holds that msi+3 ≤ msi + 1 n Theorem: If there are no 2 -cycles, then the algorithm gives a 5/3 -approximation of the optimum

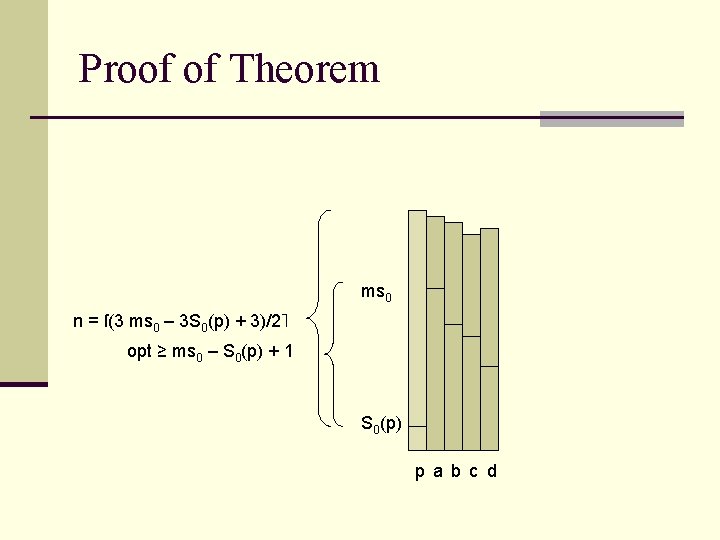
Proof of Theorem ms 0 n = ſ(3 ms 0 – 3 S 0(p) + 3)/2˥ opt ≥ ms 0 – S 0(p) + 1 S 0(p) p a b c d

Eliminating the 2 -cycles n Lemma: If at a certain stage i there are no 2 -cycles, then for all j > i, there will be no 2 -cycles at stage j n We prove that the algorithm performs optimally while there are 2 -cycles n Intuitively, if there is a 2 -cycle, then one of its vertices has the highest score, and it will always be placed in the end – until the cycle is eliminated n Once the 2 -cycles have been eliminated, our algorithm performs a 5/3 -approximation on the number of stages left n Generally we have 5/3 -approximation of the optimal solution

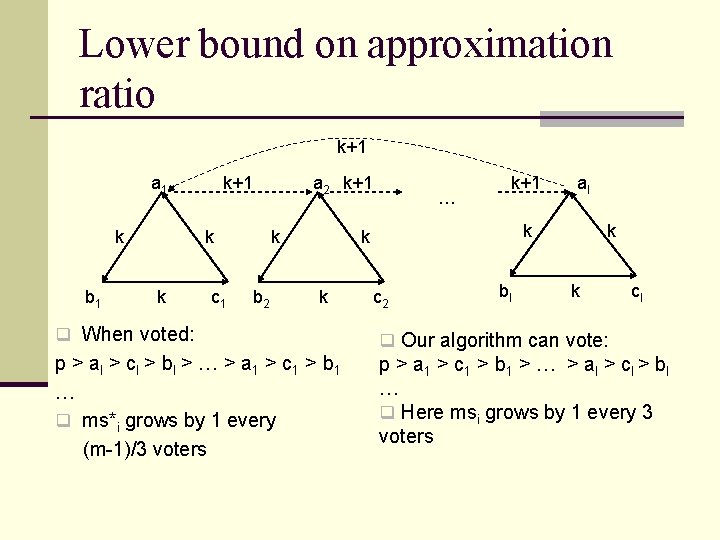
Lower bound on approximation ratio k+1 a 1 k b 1 a 2 k+1 k k c 1 k b 2 … k+1 k k k al c 2 bl k k cl q When voted: q Our algorithm can vote: p > al > cl > bl > … > a 1 > c 1 > b 1 … q ms*i grows by 1 every (m-1)/3 voters p > a 1 > c 1 > b 1 > … > a l > c l > bl … q Here msi grows by 1 every 3 voters

Simulation results n Implemented n this algorithm n the simple greedy algorithm in [2] n On average, this algorithm is a little better n On some instances, the simple greedy is better n No difference between the performance of this algorithm with and without the “additions” n Difficulties in calculating the optimum

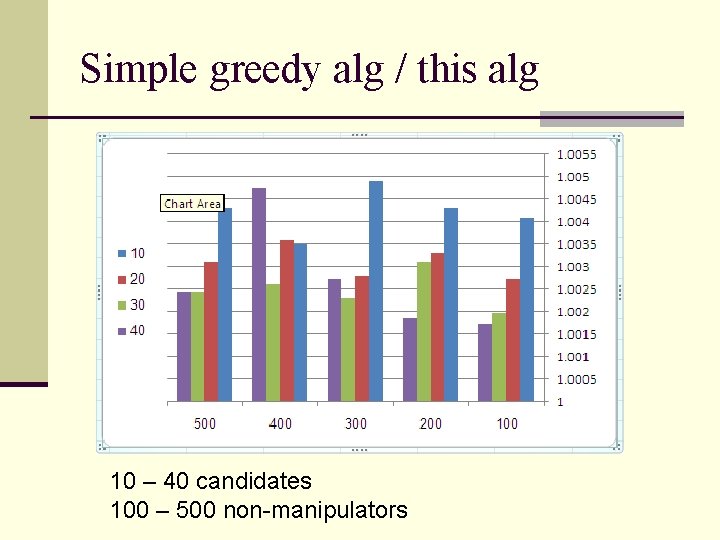
Simple greedy alg / this alg 10 – 40 candidates 100 – 500 non-manipulators

Conclusions n A new heuristic / approximation algorithm for CCUM / UCO under Maximin n Gives a 5/3 -approximation to the optimum n The lower bound on the approximation ratio of the algorithm (and any algorithm) is 1½ n Simulation results – comparison between this algorithm and the simple greedy algorithm in [2] n Future work n Prove the approx. ratio without the additions

References n [1] Complexity of Unweighted Coalitional Manipulation Under Some Common Voting Rules, Lirong Xia, Michael Zuckerman, Ariel D. Procaccia, Vincent Conitzer and Jeffrey S. Rosenschein. The Twenty-First International Joint Conference on Artificial Intelligence (IJCAI 2009), July 2009, Pasadena, California, pp. 348 -353. n [2] Algorithms for the Coalitional Manipulation Problem, Michael Zuckerman, Ariel D. Procaccia and Jeffrey S. Rosenschein. Journal of Artificial Intelligence. Volume 173, Number 2, February 2009, pp. 392 -412.

Thank You!