An Algebraic Algorithm for Weighted Linear Matroid Intersection

An Algebraic Algorithm for Weighted Linear Matroid Intersection Nick Harvey

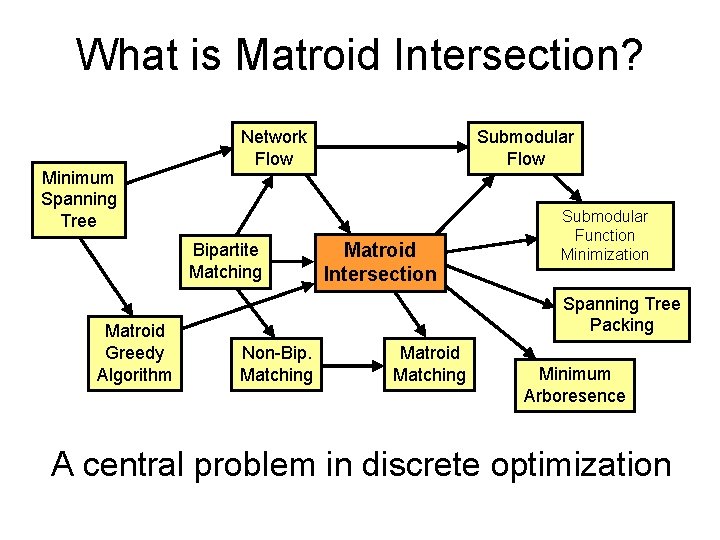
What is Matroid Intersection? Minimum Spanning Tree Network Flow Bipartite Matching Matroid Greedy Algorithm Submodular Flow Matroid Intersection Submodular Function Minimization Spanning Tree Packing Non-Bip. Matching Matroid Matching Minimum Arboresence A central problem in discrete optimization

Matroid intersection has many uses • Edge connectivity [Gabow ’ 91] • Uniprocessor scheduling [Stallman ’ 91] • Survivable network design [Balakrishnan-Magnanti-Mirchandani ’ 98] • • k-Delivery TSP [Chalasani-Motwani ’ 99] Constrained MST [Hassin-Levin ’ 04] Multicast Network Codes [Harvey-Karger-Murota ’ 05] Bounded-Degree MST [Goemans ’ 06]

An Example Problem 2 x 1 5 x 2 x 3 x 4 0 9 4 3 2 8 x 5 0 x 6 1 • Does this matrix have full rank? • Can one replace xi’s with numbers s. t. rank is maximized? • Solvable via Matroid Intersection [Murota ’ 93]

What is a Matroid? a b c 1 0 1 1 • rank = 2 • Linearly independent sets of columns I = { ∅, {a}, {b}, {c}, {a, b}, {b, c}, {a, c} }

What is a Matroid? a b c • rank = • Linearly independent sets of columns I = { ∅, {a}, {b}, {c}, {a, b}, {b, c}, {a, c} } • What is rank? Is a ∈ span({b, c})? • What properties of linear independence are needed to answer these questions?

Independence Properties Linearly independent sets of columns I = { ∅, {a}, {b}, {c}, {a, b}, {b, c}, {a, c} } Properties: 1. ∅ ∈ I 2. If A ⊆ B ∈ I then A ∈ I 3. If A, B ∈ I and |A| < |B| then ∃ b ∈ B such that A+b ∈ I

Definition A matroid is a pair (S, I) with I ⊆ 2 S satisfying the axioms 1. ∅ ∈ I 2. If A ⊆ B ∈ I then A ∈ I 3. If A, B ∈ I and |A| < |B| then ∃ b ∈ B such that A+b ∈ I

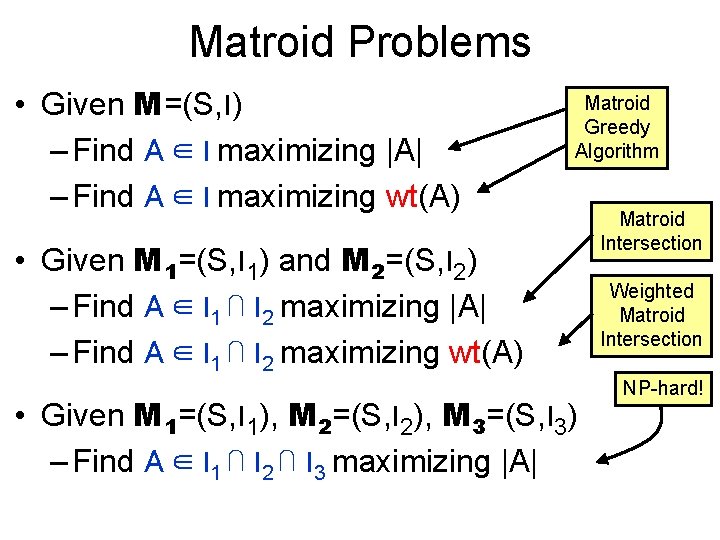
Matroid Problems • Given M=(S, I) – Find A ∈ I maximizing |A| – Find A ∈ I maximizing wt(A) Matroid Greedy Algorithm • Given M 1=(S, I 1) and M 2=(S, I 2) – Find A ∈ I 1 ⋂ I 2 maximizing |A| – Find A ∈ I 1 ⋂ I 2 maximizing wt(A) • Given M 1=(S, I 1), M 2=(S, I 2), M 3=(S, I 3) – Find A ∈ I 1 ⋂ I 2 ⋂ I 3 maximizing |A| Matroid Intersection Weighted Matroid Intersection NP-hard!

Two types of algorithms • Oracle Algorithms Access matroid by oracle queries “Is A ∈ I? ” • Linear Matroid Algorithms Input is a matrix M s. t. I is the set of linearly indep. columns of M

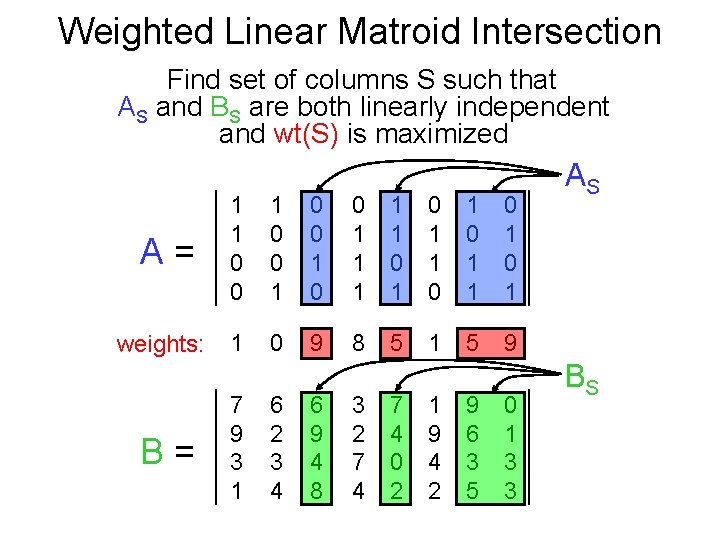
Weighted Linear Matroid Intersection Find set of columns S such that AS and BS are both linearly independent and wt(S) is maximized A= 1 1 0 0 1 1 1 0 1 0 1 weights: 1 0 9 8 5 1 5 9 B= 7 9 3 1 6 2 3 4 6 9 4 8 3 2 7 4 0 2 1 9 4 2 9 6 3 5 0 1 3 3 AS BS

Oracle Algorithm History Access matroid by oracle queries “Is A ∈ I? ” Edmonds ’ 65 -’ 70 Augmenting Paths O(nr 2) Lawler ’ 75, Edmonds ’ 79 Augmenting Paths O(nr 2) Cunningham ’ 86 “Blocking Flows” O(nr 1. 5) Shigeno-Iwata ’ 95 Dual Approximation ≈O(nr 1. 5 log(r. W)) n = |S| r = rank(S) W = max weight Grey row = unweighted algorithm

Linear Matroid Algorithm History Given a matrix M s. t. I is set of indep. columns Cunningham ’ 86 “Blocking Flows” O(nr 2 log r) Gabow-Xu ’ 89 -’ 96 “Blocking Flows” & Fast Matrix Multiplication O(nr 1. 77 log W) Harvey ’ 06 † Fast Matrix Multiplication O(nr -1) This Paper † Fast Linear System Solving for Polynomial Matrices O(nr -1 W 1+ε) matrix M has size n x r W = max weight Grey row = unweighted algorithm † Randomized, and assumes matroids can be represented over same field

Anatomy of a Weighted Optimization Algorithm e. g: Primal-Dual Method repeat adjust dual find best primal using items allowed by dual until primal is optimal • Can any fast primal alg be used here? – Want primal alg to work incrementally • Sadly, algebraic method is not incremental

Polynomial Matrices • Used in PRAM algs for matching [KUW ’ 86], [MVV ’ 87] 2 a b c 0 1 d 5 1 2 e e a f g h b 0 f g h x 1 y 2 x 2 y 2 x 3 y 5 x 4 y 0 x 5 y 1 0 0 c 0 0 0 x 6 y 0 d x 7 y 1 0 x 8 y 1 0

Polynomial Matrices • Used in PRAM algs for matching [KUW ’ 86], [MVV ’ 87] 2 a b c 0 1 d 5 1 2 e f g h a 0 3 y 2 1 y 2 6 y 5 b 2 y 0 4 y 1 0 0 c 0 0 0 3 y 0 d 1 y 1 0 4 y 1 0 e f g h Determinant = 12 y 4 + 72 y 3 Max Weight of a Matching

Polynomial Matrices • Matrix M, size n x n, each entry a degree W polynomial • Computing determinant: – On PRAM: O(log 2(n. W)) time – Sequentially: O(n 5 W 2) time [naive alg] O(n +1 W) time [interpolation] O(n W 1+ε) time [Storjohann ’ 03] Can compute max weight of a -1)W W 1+ε) time matroid intersection in O(nr perfect matching in O(n time

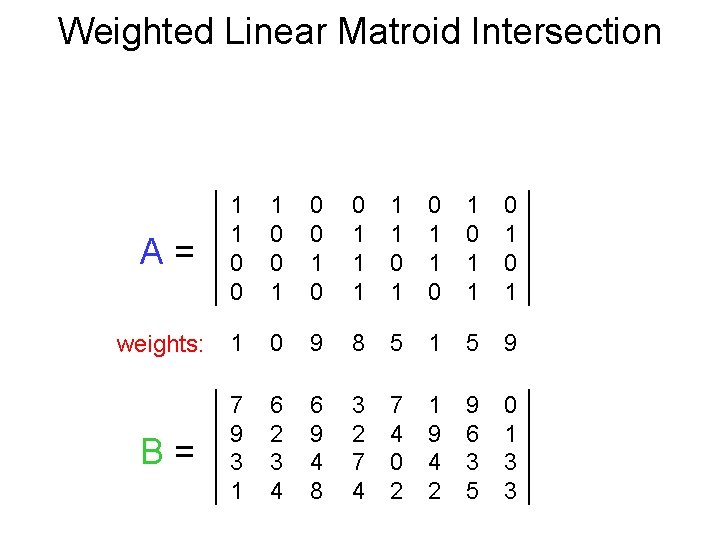
Weighted Linear Matroid Intersection A= 1 1 0 0 1 1 1 0 1 0 1 weights: 1 0 9 8 5 1 5 9 B= 7 9 3 1 6 2 3 4 6 9 4 8 3 2 7 4 0 2 1 9 4 2 9 6 3 5 0 1 3 3

Weighted Linear Matroid Intersection A 1 0 9 8 5 1 5 9

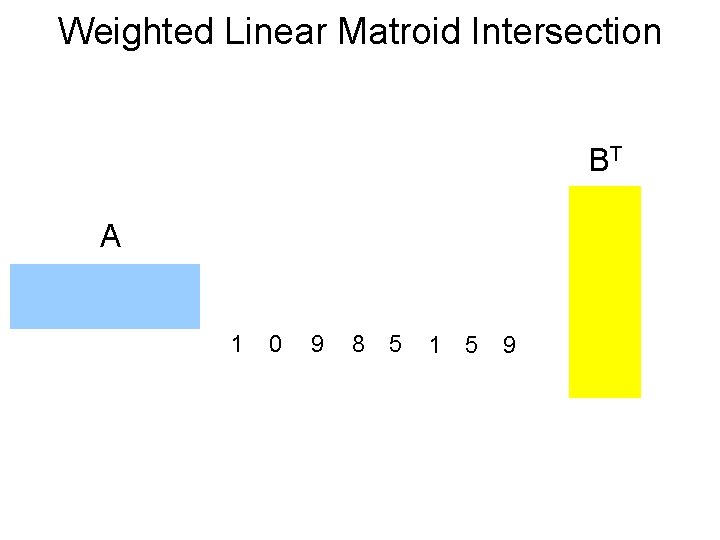
Weighted Linear Matroid Intersection BT A 1 0 9 8 5 1 5 9

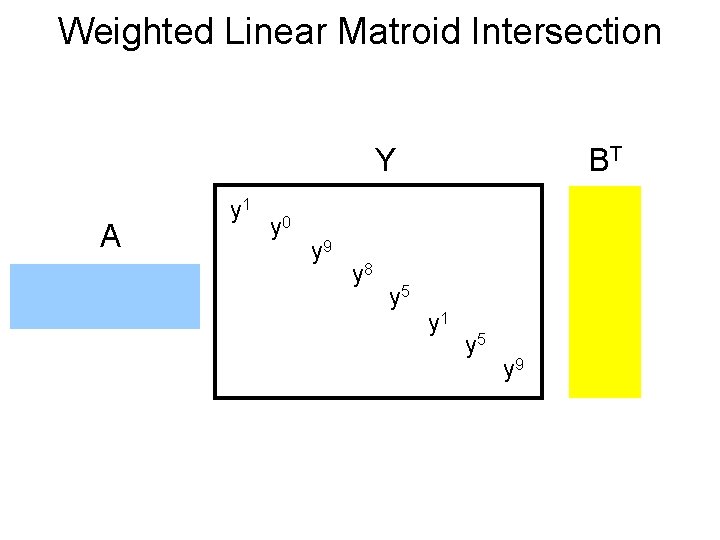
Weighted Linear Matroid Intersection Y A y 1 y 0 y 9 y 8 y 5 BT y 1 y 5 y 9

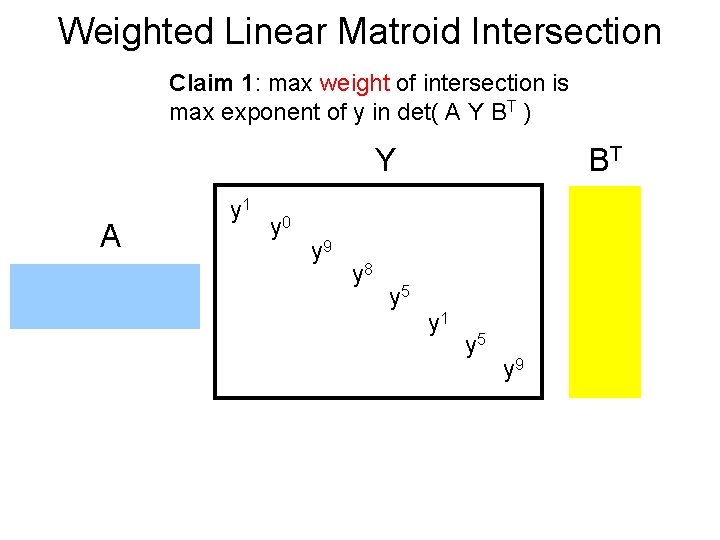
Weighted Linear Matroid Intersection Claim 1: max weight of intersection is max exponent of y in det( A Y BT ) Y A y 1 y 0 y 9 y 8 y 5 BT y 1 y 5 y 9

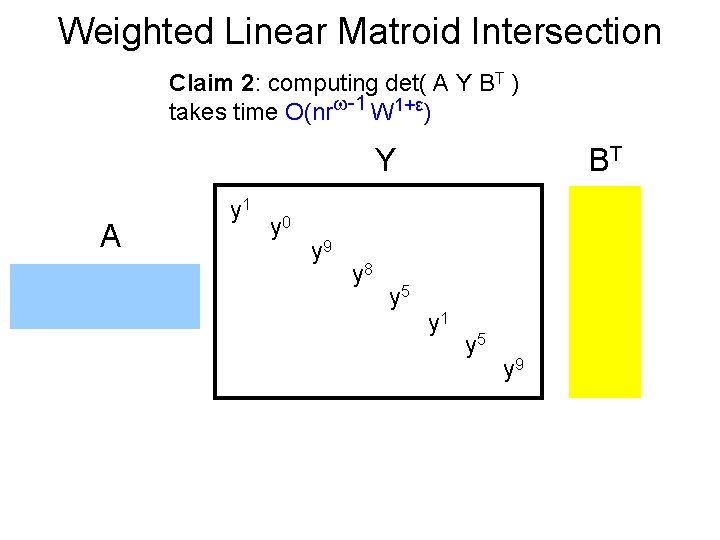
Weighted Linear Matroid Intersection Claim 2: computing det( A Y BT ) takes time O(nr -1 W 1+ε) Y A y 1 y 0 y 9 y 8 y 5 BT y 1 y 5 y 9

Using Storjohann for Optimization Problems • Can compute weight(OPT). How to find OPT? • Sankowski found a method for bipartite matching [Sankowski ’ 06] – Define a family of perturbed instances. Compute weight(OPT) for all perturbed instances. – Using these weights, compute optimum dual for original instance. – Given optimum dual, compute OPT. Find optimal bip matching in O(n W 1+ε) time

Extending Sankowski’s Method Fast algorithm (using Storjohann) [Sankowski ’ 06] Minimum Spanning Tree Network Flow Bipartite Matching Matroid Greedy Algorithm Submodular Flow Matroid Intersection Submodular Function Minimization Spanning Tree Packing Non-Bip. Matching Matroid Matching Minimum Arboresence

Extending Sankowski’s Method Fast algorithm (using Storjohann) [Sankowski ’ 06] W 1+ε) O(n Minimum Spanning log W Network Flow log W O(nr -1 W 1+ε) [This Paper] Submodular Flow Tree Bipartite Matching Matroid Greedy Algorithm Matroid Intersection Submodular Function Minimization Spanning Tree Packing Non-Bip. Matching Matroid Matching Minimum Arboresence