An advanced visualization system for planetary dynamo simulations

An advanced visualization system for planetary dynamo simulations Moritz Heimpel 1, Pierre Boulanger 2, Curtis Badke 1, Farook Al-Shamali 1, Jonathan Aurnou 3 1 Institute for Geophysical Research, Department of Physics, University of Alberta 2 Department of Computing Sciences, University of Alberta 3 Department of Earth and Space Sciences, University of California, Los Angeles

Acknowledgements Johannes Wicht (University of Goettingen) Ulrich Christensen (University of Goettingen) Gary Glatzmaier (University of California, Santa Cruz) Andreas Ritzer (University of Alberta) CNS and MACI (University of Alberta)

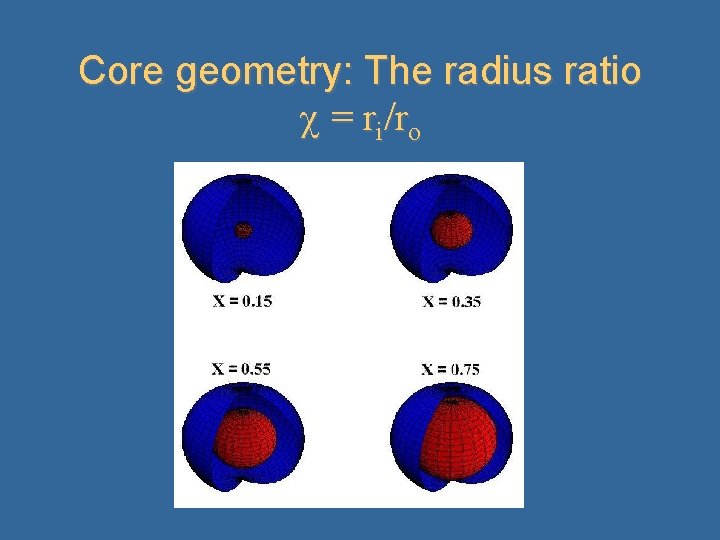
Some known dynamos Earth ( = 0. 35) Mercury ( ~ 0. 55? ) Ganymede ( ~ ? ) Io ( ~ ? ) Jupiter (c ~ 0. 85) Core radius ratio: = rinner/router

Core geometry: The radius ratio = ri/ro

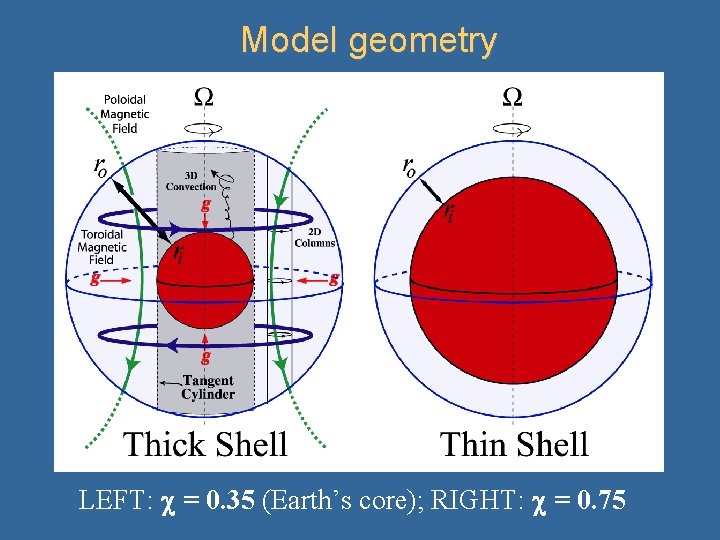
Model geometry LEFT: = 0. 35 (Earth’s core); RIGHT: = 0. 75

Some non-dimensional parameters & typical values for our numerical simulations Number Definition Value Magnetic Reynolds Rm = VD/ Ekman number E = /( D 2) 10 -3 -10 -4 Rayleigh number Ra = go TD 3/( ) 105 -107 Prandtl number Pr = / Magnetic Prandtl Pm = - Radius Ratio = ri/ro 0. 1 – 0. 9

Spherical dynamo code Originally developed by G. Glatzmaier. Modified by U. Christensen and J. Wicht. We are presently running a slightly modified version of the Wicht code, called Magic 2. Spectral transform code. Latitudinal and longitudinal directions expanded with spherical harmonics. Chebychev polynomials in radius. Time stepping via Courant criterion using a grid representation.

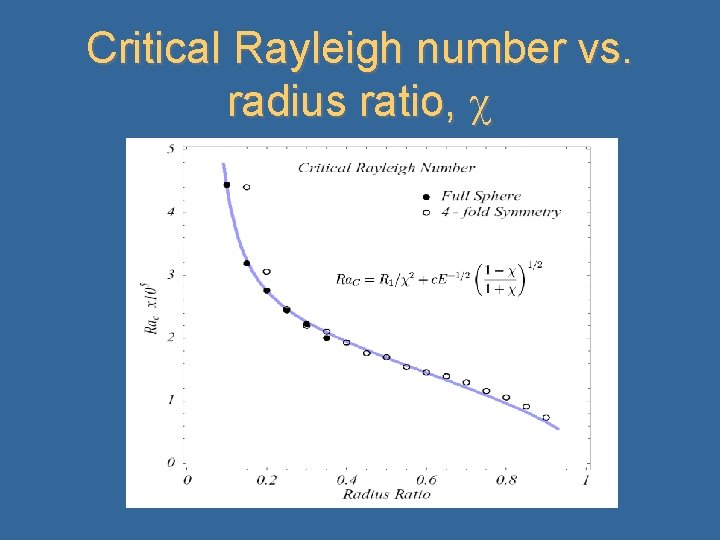
Critical Rayleigh number vs. radius ratio,

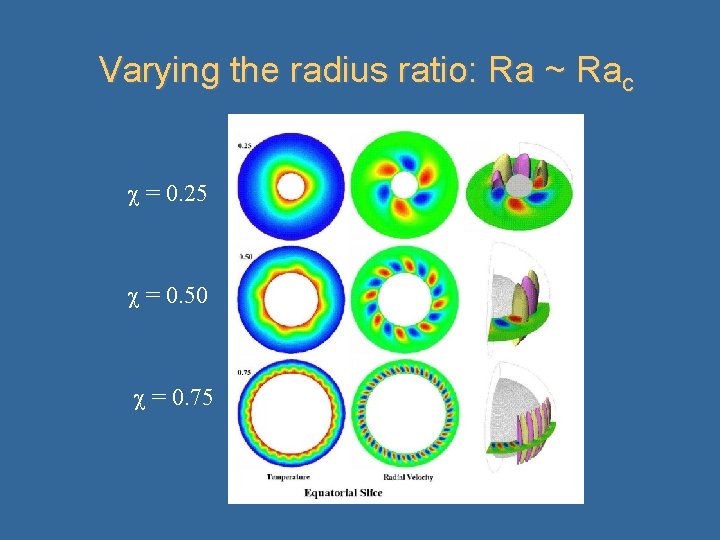
Varying the radius ratio: Ra ~ Rac = 0. 25 = 0. 50 = 0. 75

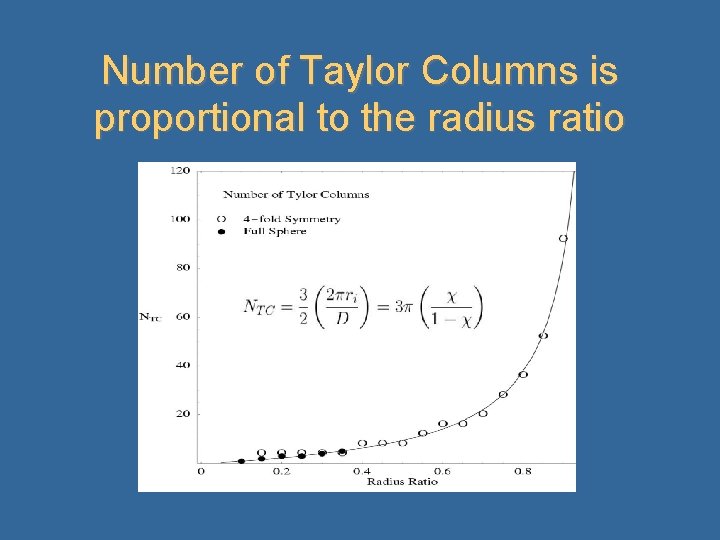
Number of Taylor Columns is proportional to the radius ratio

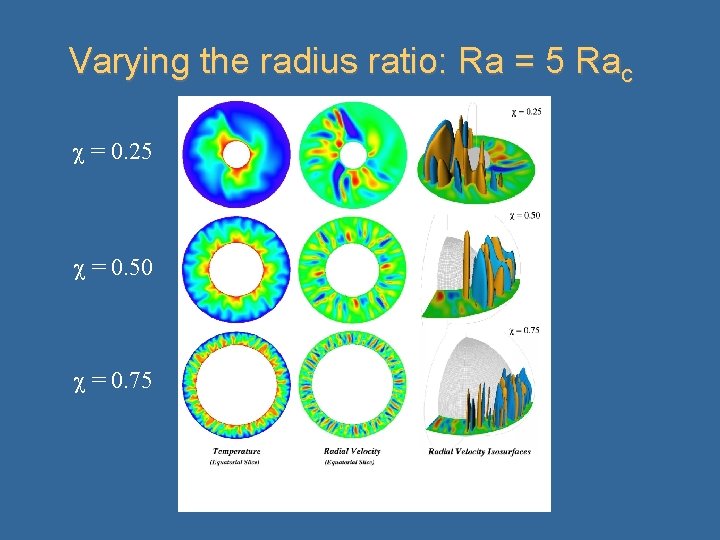
Varying the radius ratio: Ra = 5 Rac = 0. 25 = 0. 50 = 0. 75

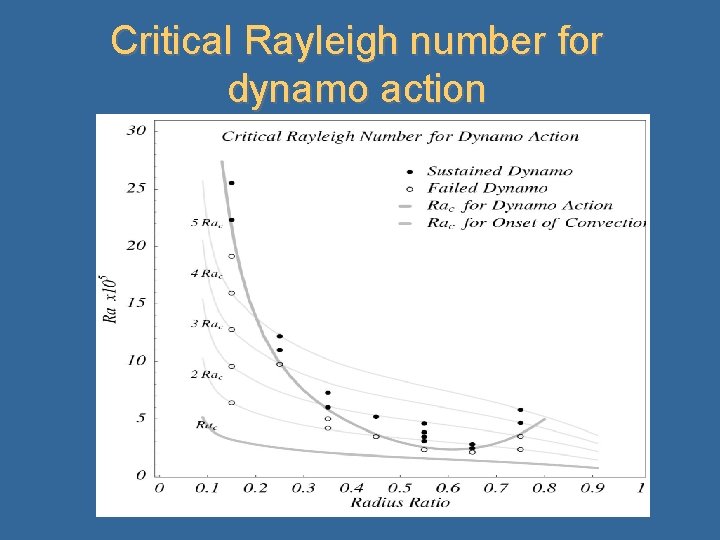
Critical Rayleigh number for dynamo action

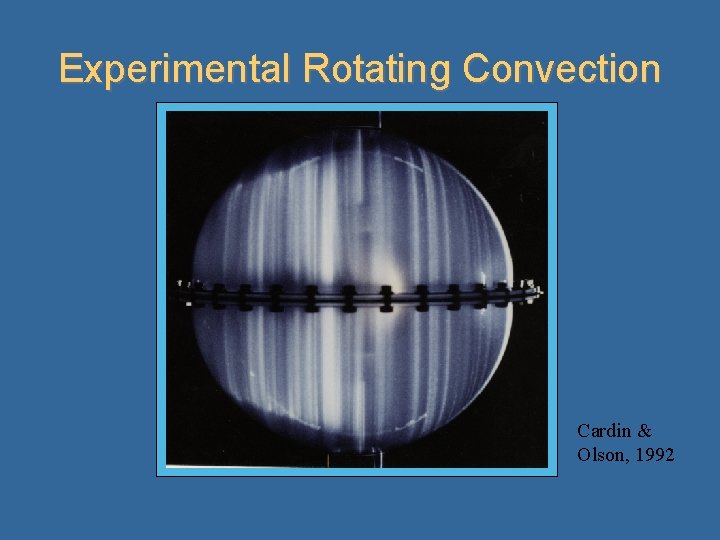
Experimental Rotating Convection Cardin & Olson, 1992

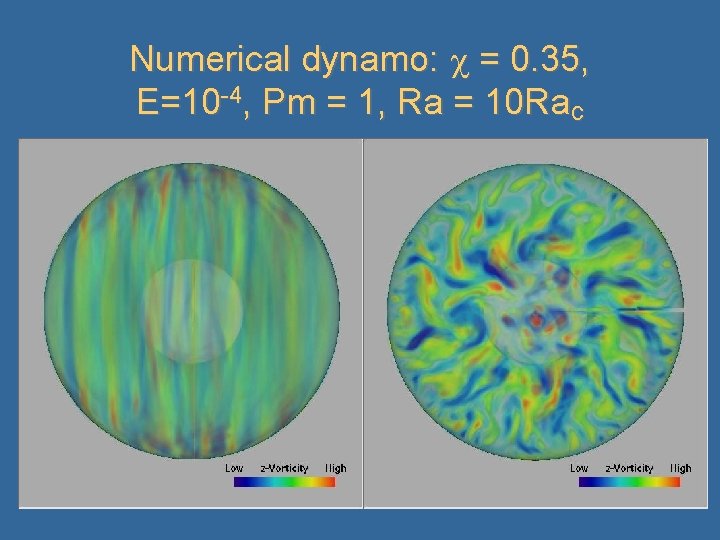
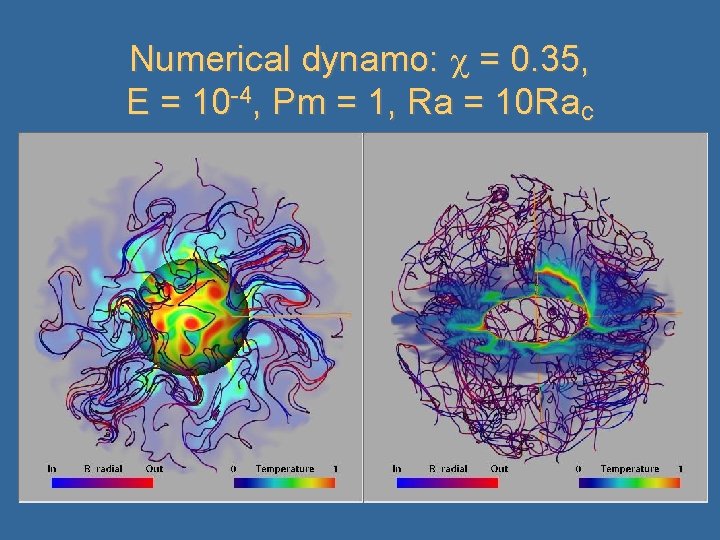
Numerical dynamo: = 0. 35, E=10 -4, Pm = 1, Ra = 10 Rac

Real time visualization: Motivation Writing and storage of solutions more expensive than running simulation Interactive adjustment of run parameters can save calculation time Fast processing and data transfer makes real time feasible Visual immersion helps interpretation of dynamical structures.

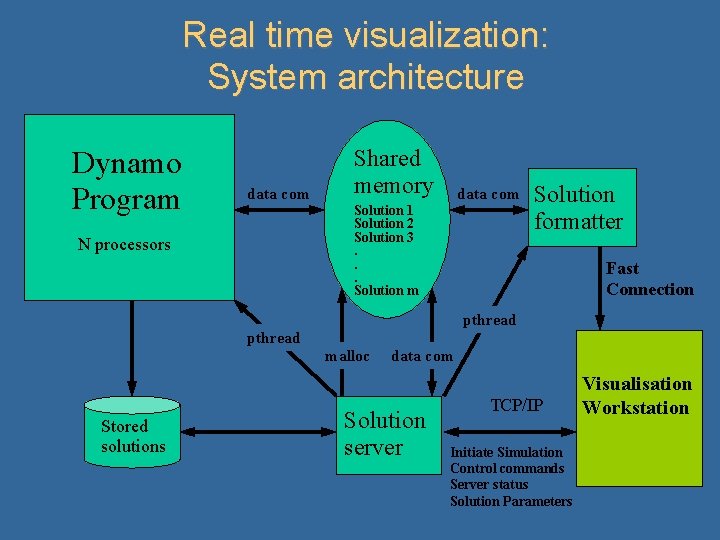
Real time visualization: System architecture Dynamo Program data com N processors Shared memory data com Solution 1 Solution 2 Solution 3. . . Solution m Solution formatter Fast Connection pthread malloc Stored solutions data com Solution server TCP/IP Initiate Simulation Control commands Server status Solution Parameters Visualisation Workstation

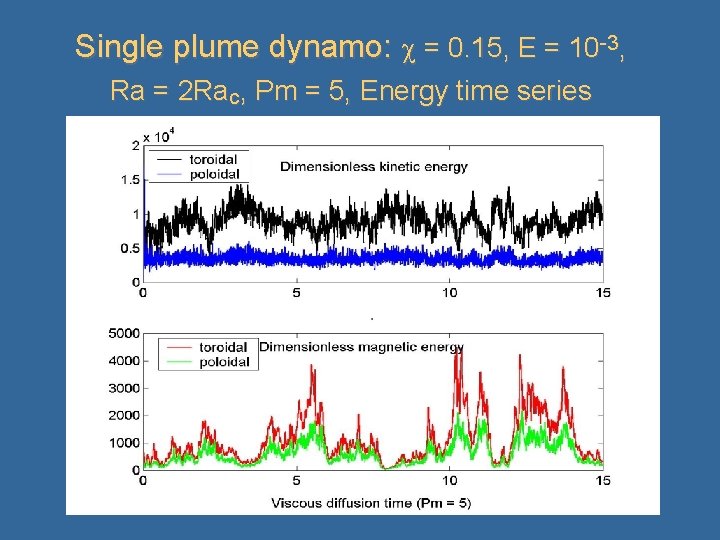
Single plume dynamo: = 0. 15, E = 10 -3, Ra = 2 Rac, Pm = 5, Energy time series

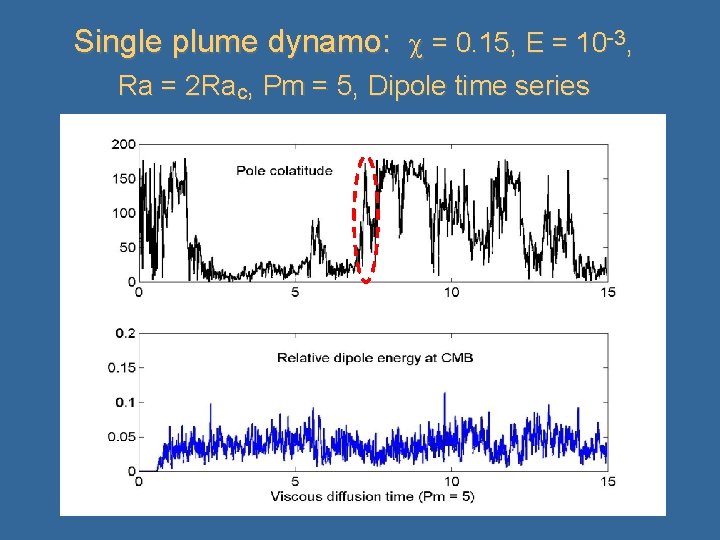
Single plume dynamo: = 0. 15, E = 10 -3, Ra = 2 Rac, Pm = 5, Dipole time series

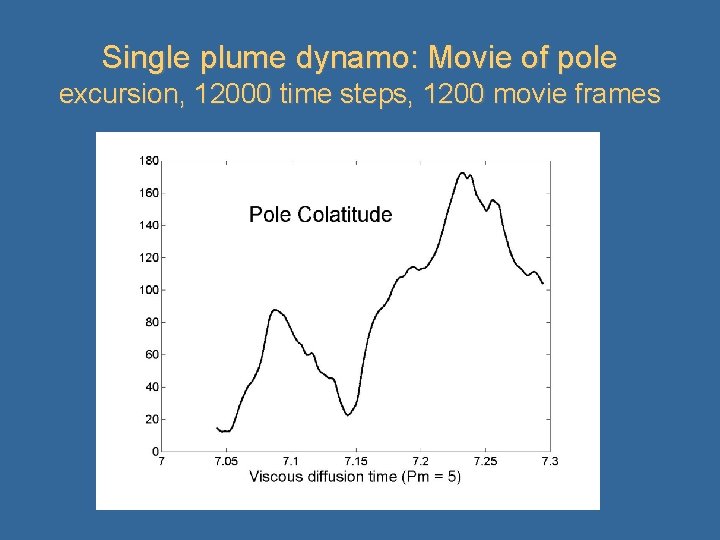
Single plume dynamo: Movie of pole excursion, 12000 time steps, 1200 movie frames

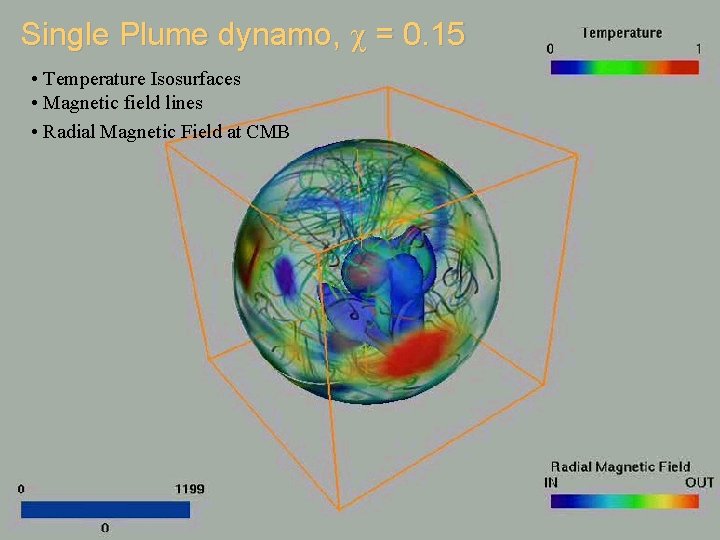
Single Plume dynamo, = 0. 15 • Temperature Isosurfaces • Magnetic field lines • Radial Magnetic Field at CMB

Numerical dynamo: = 0. 35, E = 10 -4, Pm = 1, Ra = 10 Rac

Real time visualization: Objectives Create a virtual sensory environment that helps the human brain to analyze numerical dynamos. – Bring the benefits of the experimental lab to the numerical laboratory Steering of numerical runs – Adjust parameters during a run – Adjust visualization tools (e. g. inject tracer particles) Independence of visualization system from computational code – Adaptation to various computational codes