Amplitudine ortiva e occasa Controllo della bussola RIPASSO

Amplitudine ortiva e occasa (Controllo della bussola) RIPASSO. .

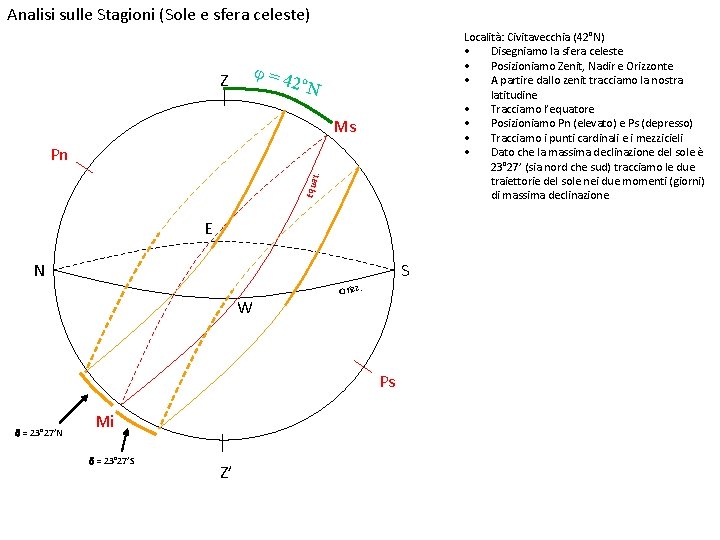
Analisi sulle Stagioni (Sole e sfera celeste) Località: Civitavecchia (42°N) • Disegniamo la sfera celeste • Posizioniamo Zenit, Nadir e Orizzonte • A partire dallo zenit tracciamo la nostra latitudine • Tracciamo l’equatore • Posizioniamo Pn (elevato) e Ps (depresso) • Tracciamo i punti cardinali e i mezzicieli • Dato che la massima declinazione del sole è 23° 27’ (sia nord che sud) tracciamo le due traiettorie del sole nei due momenti (giorni) di massima declinazione j=4 2°N Z Ms Equa t . Pn E N S W Orizz. Ps d = 23° 27’N Mi d = 23° 27’S Z’

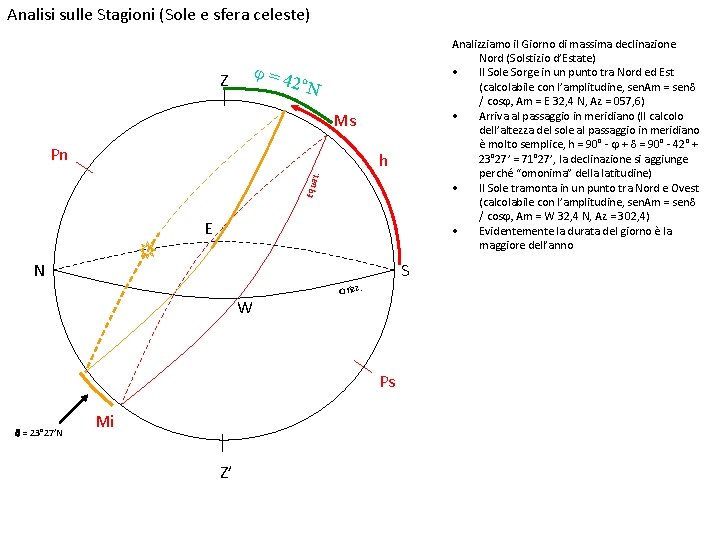
Analisi sulle Stagioni (Sole e sfera celeste) Analizziamo il Giorno di massima declinazione Nord (Solstizio d’Estate) • Il Sole Sorge in un punto tra Nord ed Est (calcolabile con l’amplitudine, sen. Am = send / cosj, Am = E 32, 4 N, Az = 057, 6) • Arriva al passaggio in meridiano (Il calcolo dell’altezza del sole al passaggio in meridiano è molto semplice, h = 90° - j + d = 90° - 42° + 23° 27’ = 71° 27’, la declinazione si aggiunge perché “omonima” della latitudine) • Il Sole tramonta in un punto tra Nord e Ovest (calcolabile con l’amplitudine, sen. Am = send / cosj, Am = W 32, 4 N, Az = 302, 4) • Evidentemente la durata del giorno è la maggiore dell’anno j=4 2°N Z Ms Pn Equa t . h E N S W Orizz. Ps d = 23° 27’N Mi Z’

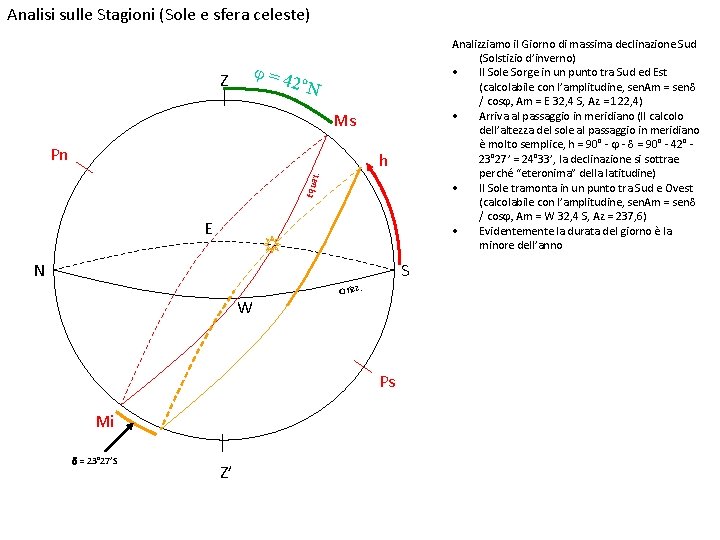
Analisi sulle Stagioni (Sole e sfera celeste) Analizziamo il Giorno di massima declinazione Sud (Solstizio d’inverno) • Il Sole Sorge in un punto tra Sud ed Est (calcolabile con l’amplitudine, sen. Am = send / cosj, Am = E 32, 4 S, Az = 122, 4) • Arriva al passaggio in meridiano (Il calcolo dell’altezza del sole al passaggio in meridiano è molto semplice, h = 90° - j - d = 90° - 42° 23° 27’ = 24° 33’, la declinazione si sottrae perché “eteronima” della latitudine) • Il Sole tramonta in un punto tra Sud e Ovest (calcolabile con l’amplitudine, sen. Am = send / cosj, Am = W 32, 4 S, Az = 237, 6) • Evidentemente la durata del giorno è la minore dell’anno j=4 2°N Z Ms Pn Equa t . h E N S W Orizz. Ps Mi d = 23° 27’S Z’

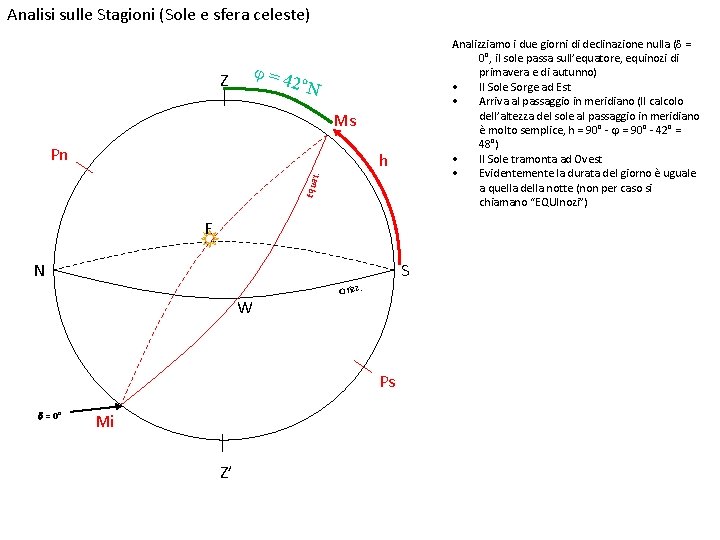
Analisi sulle Stagioni (Sole e sfera celeste) Analizziamo i due giorni di declinazione nulla (d = 0°, il sole passa sull’equatore, equinozi di primavera e di autunno) • Il Sole Sorge ad Est • Arriva al passaggio in meridiano (Il calcolo dell’altezza del sole al passaggio in meridiano è molto semplice, h = 90° - j = 90° - 42° = 48°) • Il Sole tramonta ad Ovest • Evidentemente la durata del giorno è uguale a quella della notte (non per caso si chiamano “EQUInozi”) j=4 2°N Z Ms Pn Equa t . h E N S W Orizz. Ps d = 0° Mi Z’

Amplitudine ortiva e occasa (Controllo della bussola) LEZIONE. .

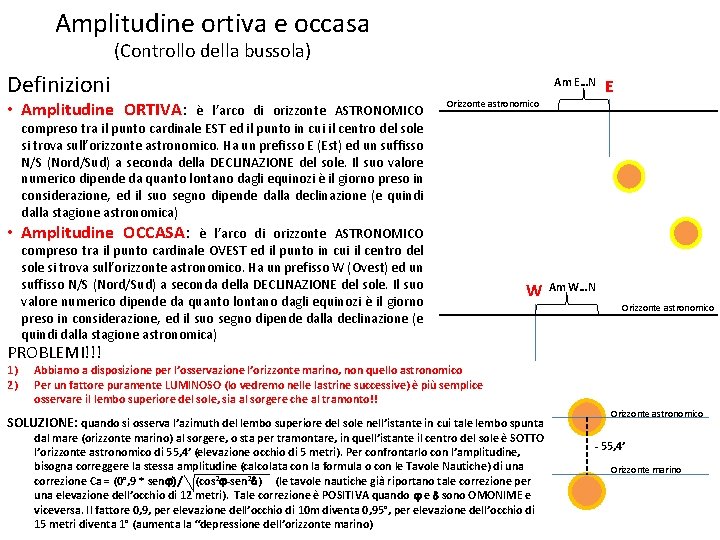
Amplitudine ortiva e occasa (Controllo della bussola) Definizioni • Amplitudine ORTIVA: • è l’arco di orizzonte ASTRONOMICO compreso tra il punto cardinale EST ed il punto in cui il centro del sole si trova sull’orizzonte astronomico. Ha un prefisso E (Est) ed un suffisso N/S (Nord/Sud) a seconda della DECLINAZIONE del sole. Il suo valore numerico dipende da quanto lontano dagli equinozi è il giorno preso in considerazione, ed il suo segno dipende dalla declinazione (e quindi dalla stagione astronomica) Amplitudine OCCASA: è l’arco di orizzonte ASTRONOMICO compreso tra il punto cardinale OVEST ed il punto in cui il centro del sole si trova sull’orizzonte astronomico. Ha un prefisso W (Ovest) ed un suffisso N/S (Nord/Sud) a seconda della DECLINAZIONE del sole. Il suo valore numerico dipende da quanto lontano dagli equinozi è il giorno preso in considerazione, ed il suo segno dipende dalla declinazione (e quindi dalla stagione astronomica) Am E…N E Orizzonte astronomico W Am W…N Orizzonte astronomico PROBLEMI!!! 1) 2) Abbiamo a disposizione per l’osservazione l’orizzonte marino, non quello astronomico Per un fattore puramente LUMINOSO (lo vedremo nelle lastrine successive) è più semplice osservare il lembo superiore del sole, sia al sorgere che al tramonto!! SOLUZIONE: quando si osserva l’azimuth del lembo superiore del sole nell’istante in cui tale lembo spunta dal mare (orizzonte marino) al sorgere, o sta per tramontare, in quell’istante il centro del sole è SOTTO l’orizzonte astronomico di 55, 4’ (elevazione occhio di 5 metri). Per confrontarlo con l’amplitudine, bisogna correggere la stessa amplitudine (calcolata con la formula o con le Tavole Nautiche) di una correzione Ca = (0°, 9 * senj)/ (cos 2 j-sen 2 d) (le tavole nautiche già riportano tale correzione per una elevazione dell’occhio di 12 metri). Tale correzione è POSITIVA quando j e d sono OMONIME e viceversa. Il fattore 0, 9, per elevazione dell’occhio di 10 m diventa 0, 95°, per elevazione dell’occhio di 15 metri diventa 1° (aumenta la “depressione dell’orizzonte marino) Orizzonte astronomico - 55, 4’ Orizzonte marino

Amplitudine ortiva e occasa (Curiosità) Etimologia degli aggettivi “ortivo” e “occaso” • ORTIVO deriva dal tardo latino “ortivum” (dall’aggettivo “ortus”) significa “CHE SORGE”, “CHE SPUNTA”. (stessa etimologia della parola “orto”) deriva dal greco “aortè” (“ ”) da “aeiro” (“io sollevo”) significa “CHE SI SOLLEVA” (stessa etimologia della parola “aorta”) • OCCASO deriva dal latino “occasum” dal verbo “occidere” (cadere) significa “caduto” (stessa etimologia di “occasione”… che (ac)cade) (stessa etimologia di “occidente”… (sole) che sta cadendo) (in italiano è diventato “accadere”) (in italiano è diventato transitivo “uccidere” …far cadere) (in italiano è diventato “ucciso” come “caduto”)

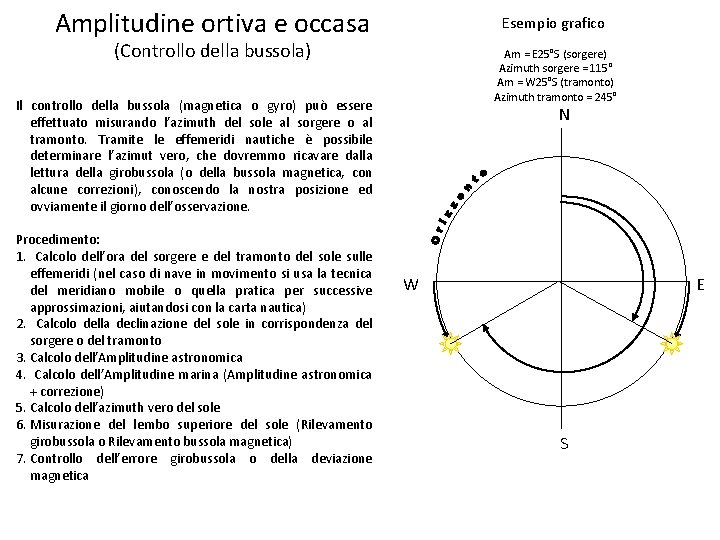
Amplitudine ortiva e occasa Esempio grafico (Controllo della bussola) Am = E 25°S (sorgere) Azimuth sorgere = 115° Am = W 25°S (tramonto) Azimuth tramonto = 245° Il controllo della bussola (magnetica o gyro) può essere effettuato misurando l’azimuth del sole al sorgere o al tramonto. Tramite le effemeridi nautiche è possibile determinare l’azimut vero, che dovremmo ricavare dalla lettura della girobussola (o della bussola magnetica, con alcune correzioni), conoscendo la nostra posizione ed ovviamente il giorno dell’osservazione. Procedimento: 1. Calcolo dell’ora del sorgere e del tramonto del sole sulle effemeridi (nel caso di nave in movimento si usa la tecnica del meridiano mobile o quella pratica per successive approssimazioni, aiutandosi con la carta nautica) 2. Calcolo della declinazione del sole in corrispondenza del sorgere o del tramonto 3. Calcolo dell’Amplitudine astronomica 4. Calcolo dell’Amplitudine marina (Amplitudine astronomica + correzione) 5. Calcolo dell’azimuth vero del sole 6. Misurazione del lembo superiore del sole (Rilevamento girobussola o Rilevamento bussola magnetica) 7. Controllo dell’errore girobussola o della deviazione magnetica N W E S

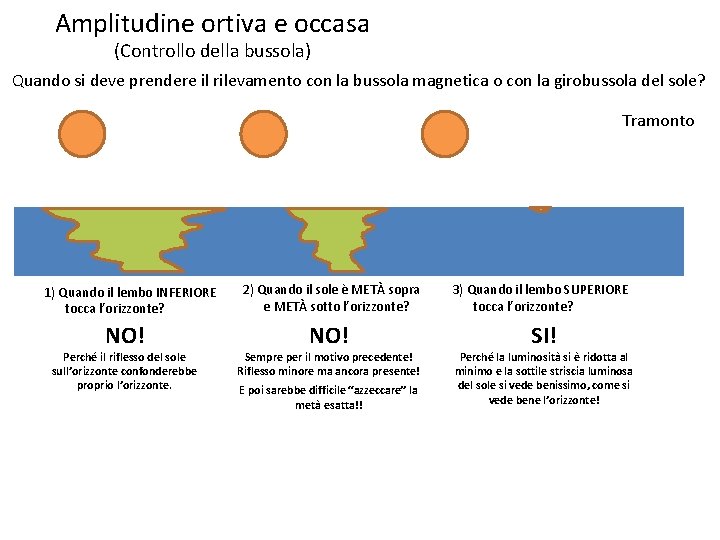
Amplitudine ortiva e occasa (Controllo della bussola) Quando si deve prendere il rilevamento con la bussola magnetica o con la girobussola del sole? Tramonto 1) Quando il lembo INFERIORE tocca l’orizzonte? NO! Perché il riflesso del sole sull’orizzonte confonderebbe proprio l’orizzonte. 2) Quando il sole è METÀ sopra e METÀ sotto l’orizzonte? 3) Quando il lembo SUPERIORE tocca l’orizzonte? NO! SI! Sempre per il motivo precedente! Riflesso minore ma ancora presente! E poi sarebbe difficile “azzeccare” la metà esatta!! Perché la luminosità si è ridotta al minimo e la sottile striscia luminosa del sole si vede benissimo, come si vede bene l’orizzonte!

NOTA BENE: per il sorgere bisogna fare bene il calcolo dell’orario e dell’azimuth vero del sole al sorgere, così da prepararsi qualche minuto prima con la bussola. Il momento più adatto è il primo a verificarsi!!!! Sorgere

Amplitudine ortiva e occasa (Controllo della bussola) Esempio 1 (dalle Effemeridi del 2010) Osservatore: j 45°N – l 015°E (nei calcoli non si tiene conto dell’ora legale) Giorno 21 marzo 2010 (equinozio di primavera) Ora sorgere: 0602/A Declinazione sorgere (ore 0502 delle Effemeridi): 00° 11’. 3 N Amplitudine ortiva astronomica (sen. Am = send / cosj) = E 0°, 229 N Amplitudine ortiva marina = E 0°, 229 N + Ca = E 0°, 229 N + (+0, 7) = 0°, 929 Azimuth del sole al sorgere = 089°, 071 ≈ 089°, 1 (Rilevamento vero del sole al sorgere) Ora tramonto 1813/A Declinazione tramonto (ore 1713 delle Effemeridi): 00° 23’. 4 N Amplitudine ortiva atronomica (sen. Am = send / cosj) = W 0°, 551 N Amplitudine ortiva marina = W 0°, 551 N + Ca = W 0, 551 N + (+0, 7) = W 1, 251 Azimuth del sole al sorgere = 271°, 251 ≈ 271°, 3 (Rilevamento vero del sole al tramonto) Esempio con la girobussola: al tramonto, con la girobussola, misuriamo un Rlgb (rilevamento girobussola) del sole pari a 271°. Questo vuol dire che la Girobussola ha un errore pari a +0, 3° (la formula dice Rlgb + b = Rlv e cioè b = Rlv - Rlgb) L’errore della girobussola inferiore al grado è trascurabile.

Amplitudine ortiva e occasa (Controllo della bussola) Esempio 2 (dalle Effemeridi del 2010) Osservatore: j 45°N – l 015°E (nei calcoli non si tiene conto dell’ora legale) Giorno 21 giugno 2010 (solstizio d’estate) Ora sorgere: 0413/A Declinazione sorgere (ore 0313 delle Effemeridi): 23° 26’. 3 N Amplitudine ortiva astronomica (sen. Am = send / cosj) = E 34°, 21 N Amplitudine ortiva marina = E 34°, 21 N + Ca = E 34°, 21 N + (+0, 7) = E 34, 91 N Azimuth del sole al sorgere = 055°, 09 ≈ 055°, 1 (Rilevamento vero del sole al sorgere) Ora tramonto 1951/A Declinazione tramonto (ore 1851 delle Effemeridi): 23° 26’. 3 N Amplitudine ortiva astronomica (sen. Am = send / cosj) = W 34°, 21 N Amplitudine ortiva marina = W 34, 21 N + Ca = W 34, 21 N + (+0, 7) = W 34, 91 N Azimuth del sole al sorgere = 304°, 91° ≈ 304°, 9 (Rilevamento vero del sole al tramonto) Esempio con la bussola magnetica: al tramonto, con la bussola magnetica, misuriamo un Rilb (rilevamento bussola) del sole pari a 310°. La declinazione magnetica (letta sulla carta e aggiornata) è 2, 5°W. Questo vuol dire che la deviazione magnetica relativa alla PRORA Magnetica che stiamo mantenendo è pari a 304, 9 – 310 – (- 2, 5) = -2, 6° (la formula dice Rilb + d = Rlv e cioè d = Rlv – Rilb – d) Adesso bisognerebbe andare a controllare se la tabella delle deviazioni riporta per la nostra prora magnetica (esempio Pm =188°) il valore di deviazione pari a -2, 6°

Quali sono i LIMITI dell’Amplitudine? Quando l’osservatore ha una latitudine in valore assoluto MAGGIORE di 66° 33’ (circoli polari) in alcuni giorni dell’anno il sole non tramonta (cioè rimane sopra l’orizzonte, a cavallo del solstizio d’estate) oppure non sorge (cioè rimane sotto l’orizzonte, a cavallo del solstizio d’inverno). Per la latitudine dei poli (90°) ovviamente il sole sorge una volta l’anno esattamente a Est (l’equinozio di primavera) e tramonta una volta l’anno esattamente a Ovest (l’equinozio d’autunno). Ai poli ci sono 6 mesi di buio e 6 mesi di luce. Dal punto di vista matematico, tutto ciò si verifica quando il seno della declinazione risulta essere maggiore del coseno della latitudine. Ciò si verifica solo quando la latitudine è maggiore appunto di 66° 33’. In questo caso il seno dell’amplitudine risulterebbe maggiore di uno e ovviamente non avrebbe senso. Circolo polare artico Il giorno polare durante la stagione “di luce”

Se l’osservatore si trova con latitudine nord, maggiore di 23° 27’ (bisogna escludere la zona tropicale in quanto al passaggio in meridiano il sole si trova molto vicino allo zenith), allora si possono controllare la bussola magnetica e la girobussola anche con il passaggio in meridiano del sole. Solo che bisogna calcolarlo con molta precisione (in navigazione con il metodo del meridiano mobile del sole, argomento che tratteremo a fine anno), anche perché il sole sembra non muoversi a cavallo del passaggio in meridiano per circa 4/5 minuti. Al passaggio in meridiano il sole è posizionato per SUD. Ovviamente vale il contrario per latitudini sud. Inoltre lo strumento deve essere dotato di uno specchio oscurato, permetterne l’uso in posizione orizzontale e per evitare che l’osservatore si accechi con la luminosità del sole Ripetitori Gyro con lo specchietto oscurato per l’osservazione del sole al passaggio in meridiano

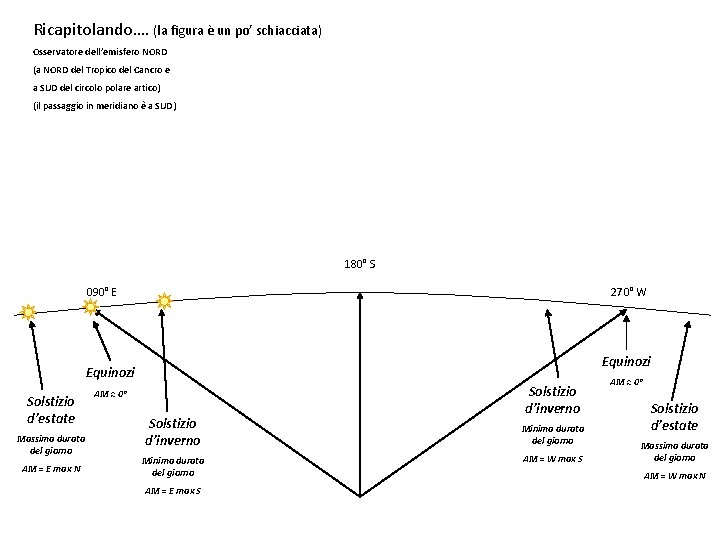
Ricapitolando…. (la figura è un po’ schiacciata) Osservatore dell’emisfero NORD (a NORD del Tropico del Cancro e a SUD del circolo polare artico) (il passaggio in meridiano è a SUD) 180° S 090° E 270° W Equinozi Solstizio d’estate Massima durata del giorno AM = E max N AM ≈ 0° Solstizio d’inverno Minima durata del giorno AM = E max S Solstizio d’inverno Minima durata del giorno AM = W max S AM ≈ 0° Solstizio d’estate Massima durata del giorno AM = W max N

Amplitudine ortiva e occasa (Controllo della bussola) ESERCIZIO. .

Esercizio di astronomia Il Com. te Roger Moses della Marina Mercantile Sudafricana, dopo una lunga prigionia durata molti mesi, viene abbandonato (dai Pirati che hanno sequestrato la sua nave) nell’arcipelago di Capo Verde, su un’Isola disabitata chiamata “Raso Islet” (16° 36’N – 024° 36’W). Gli viene concesso di portare con sé solo alcuni effetti personali, dei viveri per 7 giorni, una bussola magnetica portatile, una carta nautica dell’isola, una calcolatrice scientifica e le Effemeridi nautiche del 2016. Avendo completamente perso la nozione del tempo durante la prigionia in isolamento, il Comandante decide di effettuare due misurazioni dell’azimuth del sole al tramonto distanza di 6 giorni l’una dall’altra (dalla sua posizione riesce a vedere solo il tramonto, perché l’alba è nascosta dall’isola stessa). La declinazione magnetica riportata sulla carta è: d(20040) = 1° 12’E (decr. ann. 18’) 1ª osservazione 2ª osservazione Rlm = 293, 1 Rlm = 293, 8 Dopo la seconda osservazione il Comandante Moses è in grado di stabilire il giorno esatto sia della prima che della seconda osservazione.