Amirkabir University of Technology MATHEMATICAL MODEL FOR ACTION

Amirkabir University of Technology MATHEMATICAL MODEL FOR ACTION POTENTIAL Supervisor: Dr Gharibzadeh Designed by Yashar Sarbaz 1
2
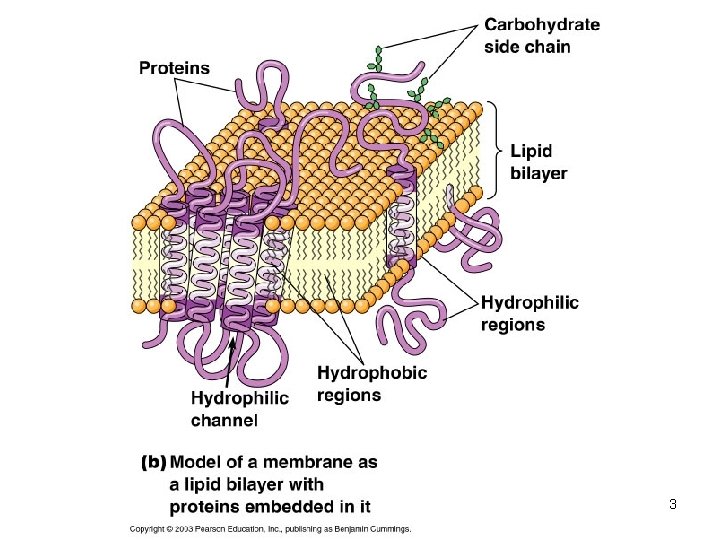
3
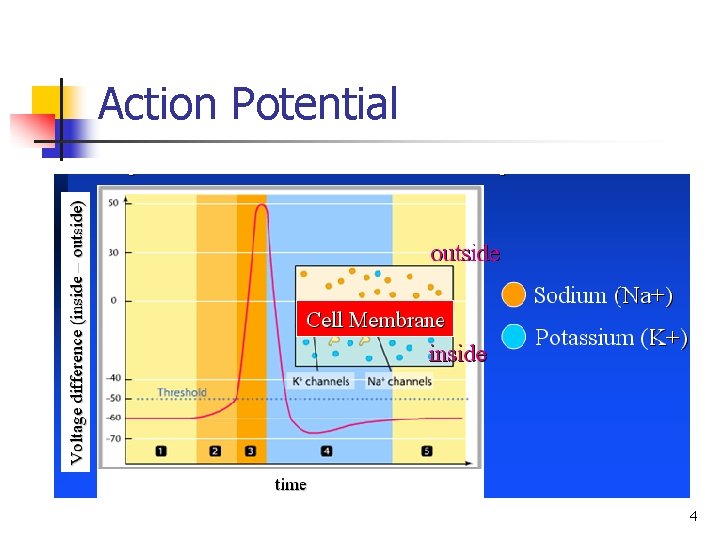
Action Potential 4
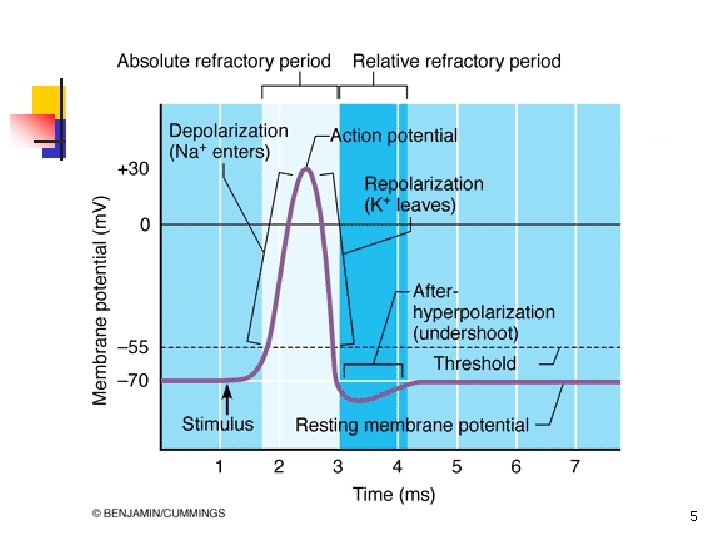
5
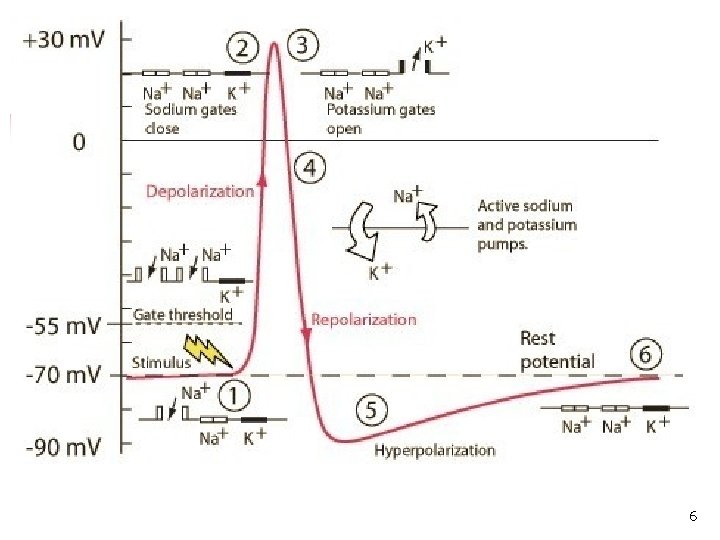
6
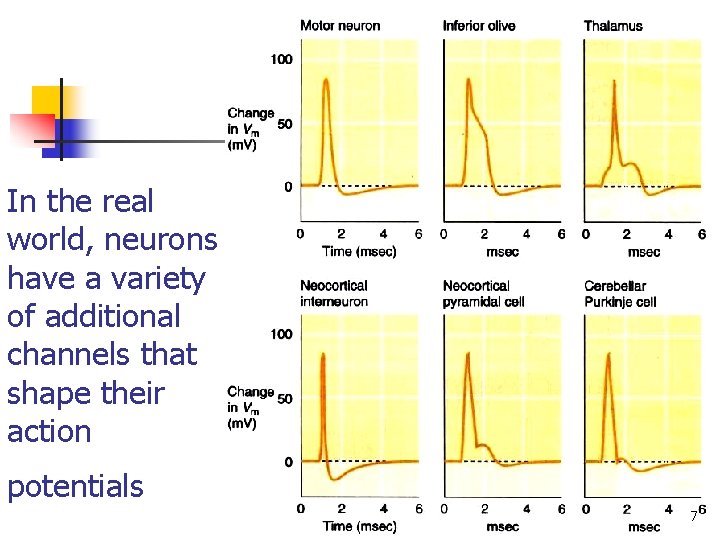
In the real world, neurons have a variety of additional channels that shape their action potentials 7

Attention 8

A. L. HODGKIN and A. F. HUXLEY The Nobel Prize in Physiology or Medicine 1963 (with Eccles): "for their discoveries concerning the ionic mechanisms involved in excitation and inhibition in the 9 peripheral and central portions of the nerve cell membrane"
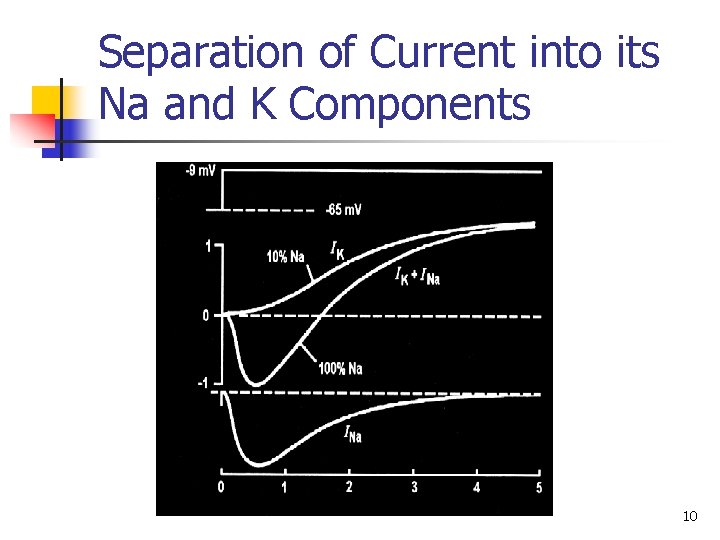
Separation of Current into its Na and K Components 10

HH Experiments in two Case n Normal Seawater n Low Na Seawater: Replace 90% sodium chloride by choline chloride while K and remaining chloride ions are unchanged 11

Three Assumption of HH 1. T: Time of peak inward current 2. Same voltage clamp but different 3. 12

Calculating Current of Na and K 13

HH Equations 14
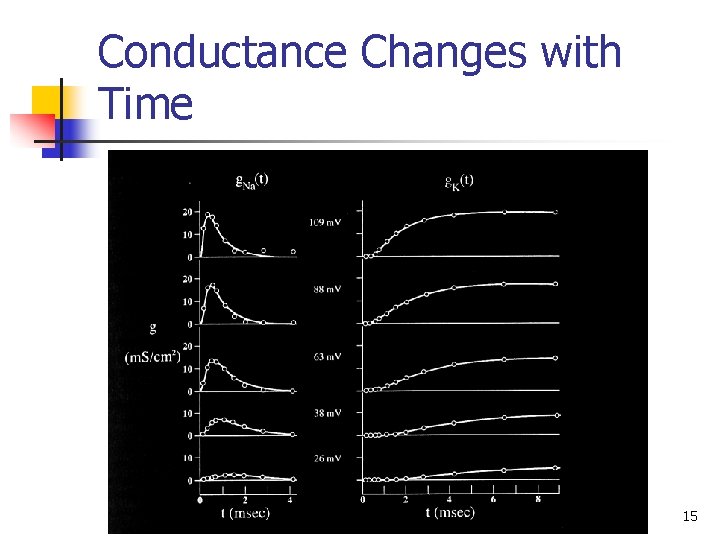
Conductance Changes with Time 15

The Hodgkin-Huxley Model n Central concept of model: Define three state variables that represent (or “control”) the opening and closing of ion channels n n n m controls Na channel opening h controls Na channel closing n controls K channel opening 16
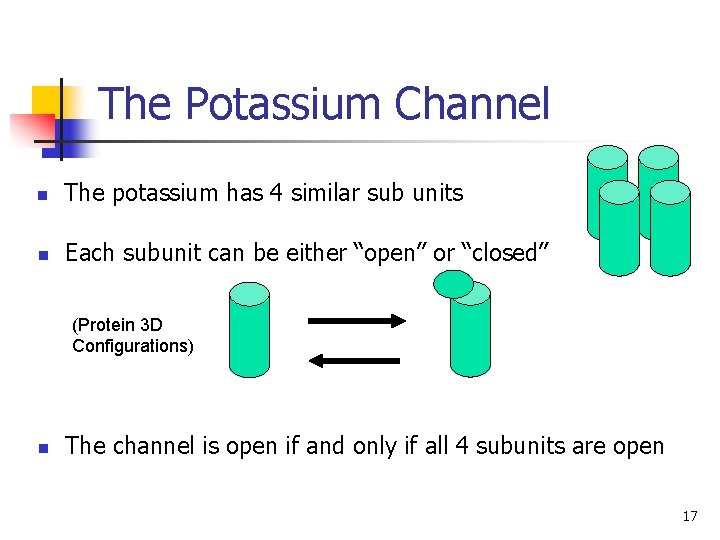
The Potassium Channel n The potassium has 4 similar sub units n Each subunit can be either “open” or “closed” (Protein 3 D Configurations) n The channel is open if and only if all 4 subunits are open 17

The Potassium Channel n The probability of a subunit being open: n The probability of the channel being open: n The conductance of a patch of membrane to K+ when all channels are open: (Constant obtained by experiments) n The conductance of a patch of membrane to K+ when the probability of a subunit being open is n: 18
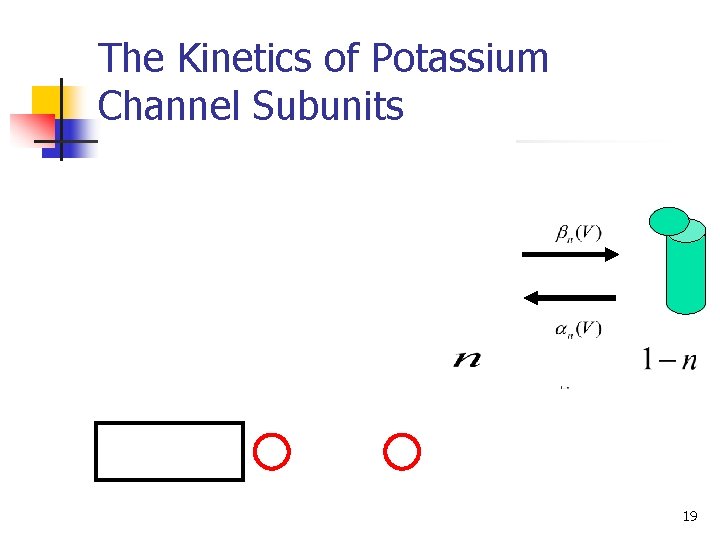
The Kinetics of Potassium Channel Subunits 19
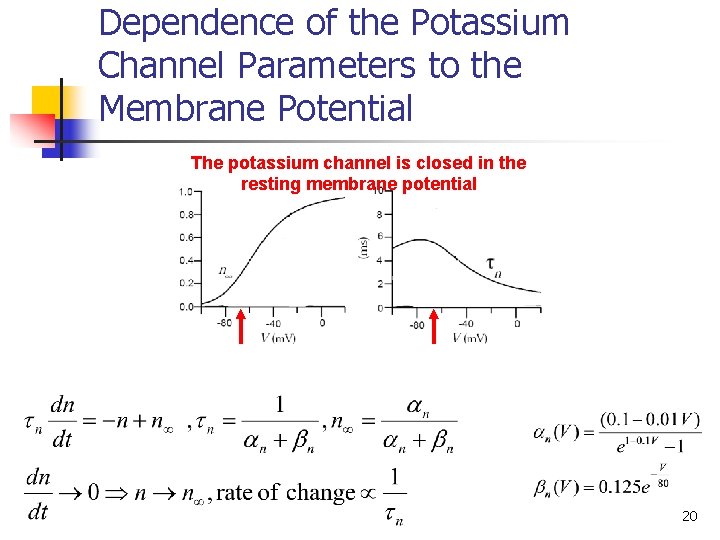
Dependence of the Potassium Channel Parameters to the Membrane Potential The potassium channel is closed in the resting membrane potential 20

Mathematical Model for K : Fraction of Open Channels : Conductance When all Channels are Open 21

Calculating n n Assuming n to Obey First Order Kinetics: 22

Solving n Equation 23

Curve Fitting for Rate Constants 24
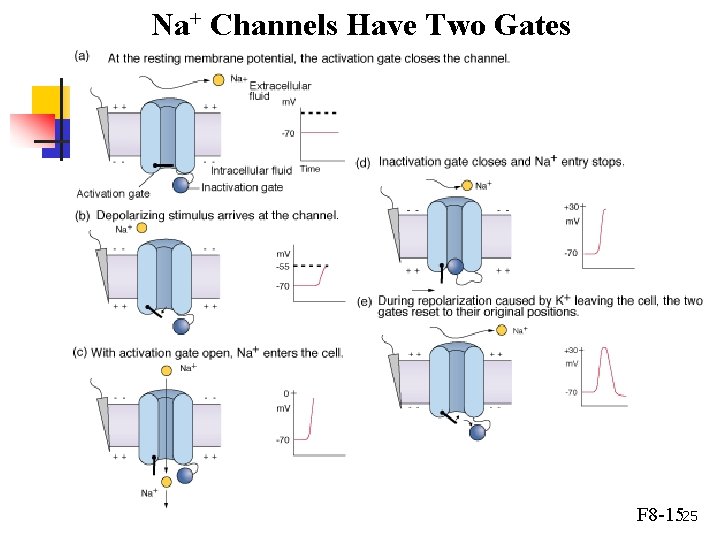
Na+ Channels Have Two Gates F 8 -1525

The Sodium Channel n n The potassium has 3 similar fast subunits and a single slow subunit Each subunit can be either “open” or “closed” (Protein 3 D Configurations) n The channel is open if and only if all 4 subunits are open 26

The Sodium Channel n The probability of a fast subunit being open: n The probability of a slow subunit being open: n The probability of the channel being open: n n The conductance of a patch of membrane to Na+ when all channels are open: (Constant obtained by experiments) The conductance of a patch of membrane to Na+ : 27
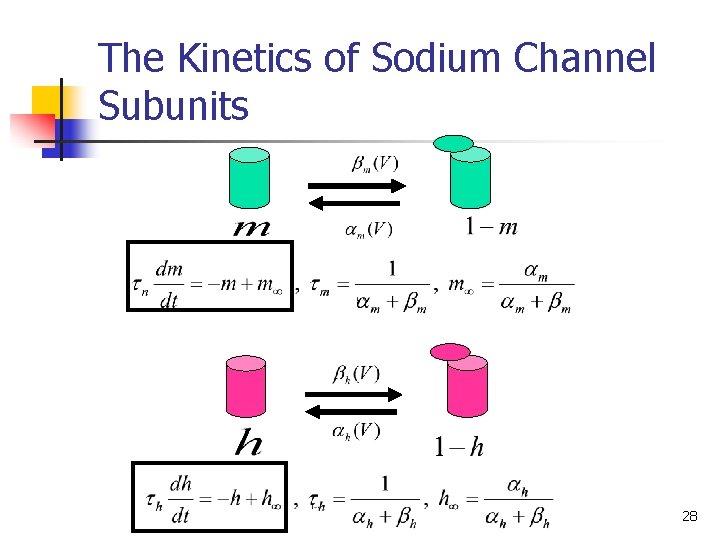
The Kinetics of Sodium Channel Subunits 28
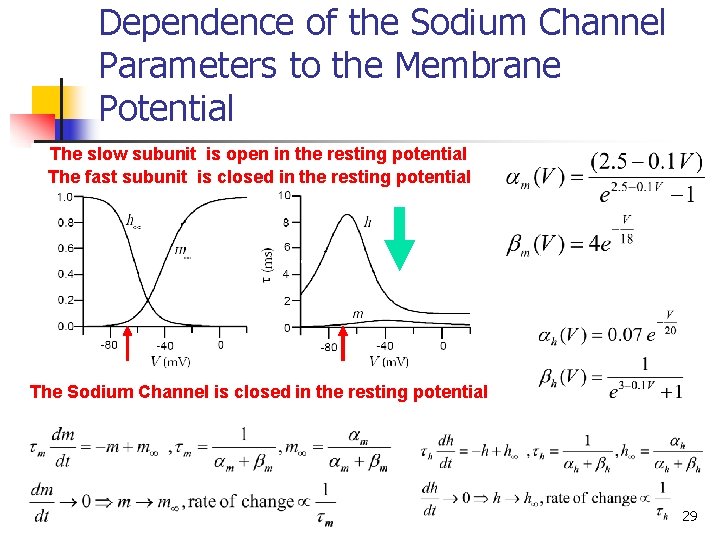
Dependence of the Sodium Channel Parameters to the Membrane Potential The slow subunit is open in the resting potential The fast subunit is closed in the resting potential The Sodium Channel is closed in the resting potential 29
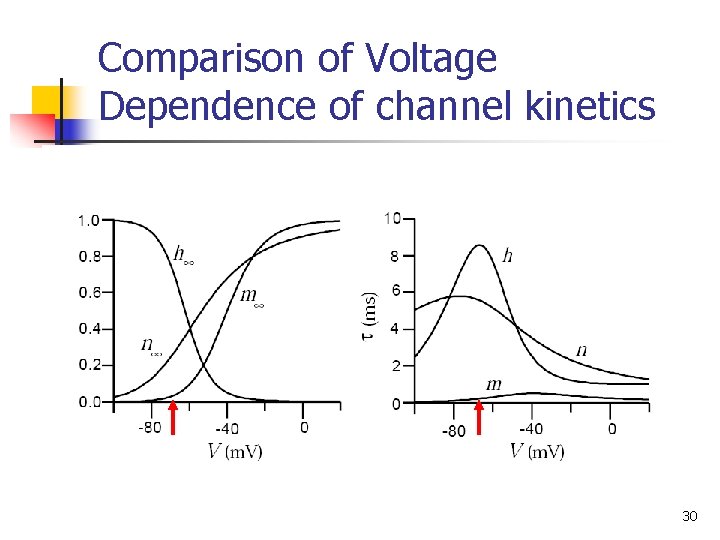
Comparison of Voltage Dependence of channel kinetics 30

Mathematical Model for Na 31

Mathematical Model for Na 32

Solving m, h Equations 33

Solving m, h Equations 34

Border Condition For Na Channels in n n In the Steady State Conductance of Na is Near the Zero and Since m is increasing Function, then: At the Rest Conductance of Na is relatively Slow, So: 35

Main Relation for 36

Curve Fitting for Rate Constants 37

Curve Fitting for Rate Constants 38

Obtaining H for all V 39
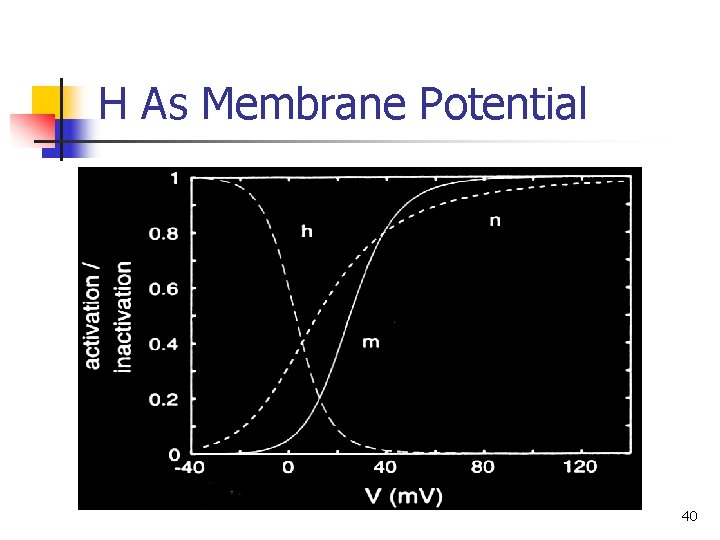
H As Membrane Potential 40

Total Current of Membrane 41
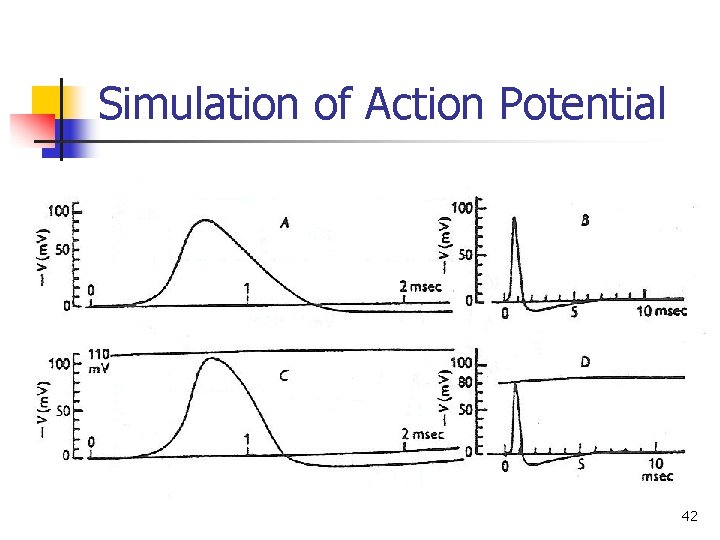
Simulation of Action Potential 42
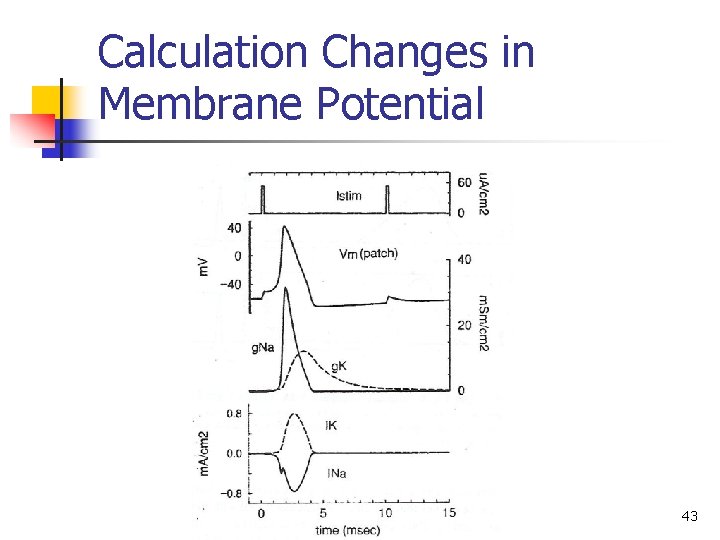
Calculation Changes in Membrane Potential 43

44
- Slides: 44