Ambiguity Precedence Associativity TopDown Parsing Lecture 9 10

Ambiguity, Precedence, Associativity & Top-Down Parsing Lecture 9 -10 (From slides by G. Necula & R. Bodik) 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 1

Administrivia • Team assignments this evening for all those not listed as having one. • HW#3 is now available, due next Tuesday morning (Monday is a holiday). 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 2

Remaining Issues • How do we find a derivation of s ? • Ambiguity: what if there is more than one parse tree (interpretation) for some string s ? • Errors: what if there is no parse tree for some string s ? • Given a derivation, how do we construct an abstract syntax tree from it? 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 3

Ambiguity • Grammar E E + E | E * E | ( E ) | int • Strings int + int * int + int 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 4
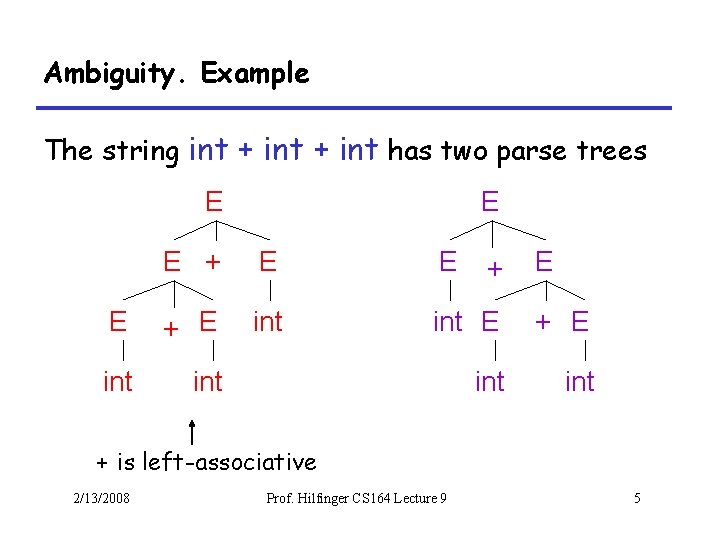
Ambiguity. Example The string int + int has two parse trees E E E + E int int + E + is left-associative 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 5

Ambiguity. Example The string int * int + int has two parse trees E E E + E E E * E int E + E int int * E * has higher precedence than + 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 6

Ambiguity (Cont. ) • A grammar is ambiguous if it has more than one parse tree for some string – Equivalently, there is more than one rightmost or leftmost derivation for some string • Ambiguity is bad – Leaves meaning of some programs ill-defined • Ambiguity is common in programming languages – Arithmetic expressions – IF-THEN-ELSE 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 7

Dealing with Ambiguity • There are several ways to handle ambiguity • Most direct method is to rewrite the grammar unambiguously E E+T|T T T * int | ( E ) • Enforces precedence of * over + • Enforces left-associativity of + and * 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 8
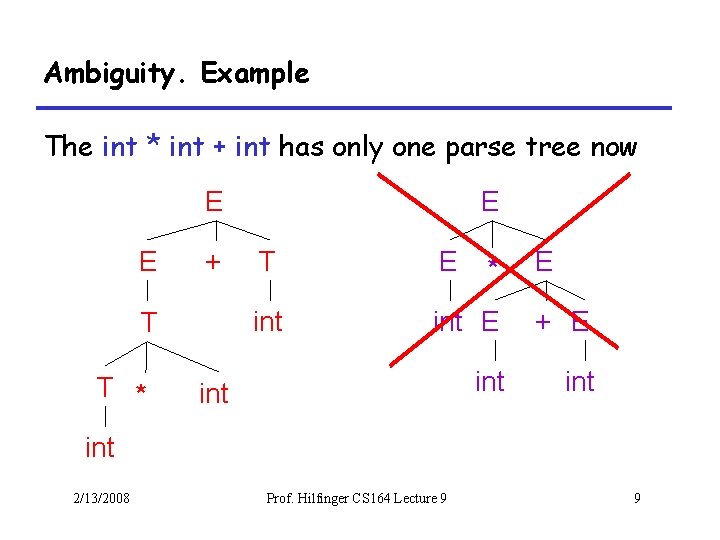
Ambiguity. Example The int * int + int has only one parse tree now E E + T T * E T E int E + E int int * E int 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 9

Ambiguity: The Dangling Else • Consider the grammar E if E then E | if E then E else E | OTHER • This grammar is also ambiguous 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 10
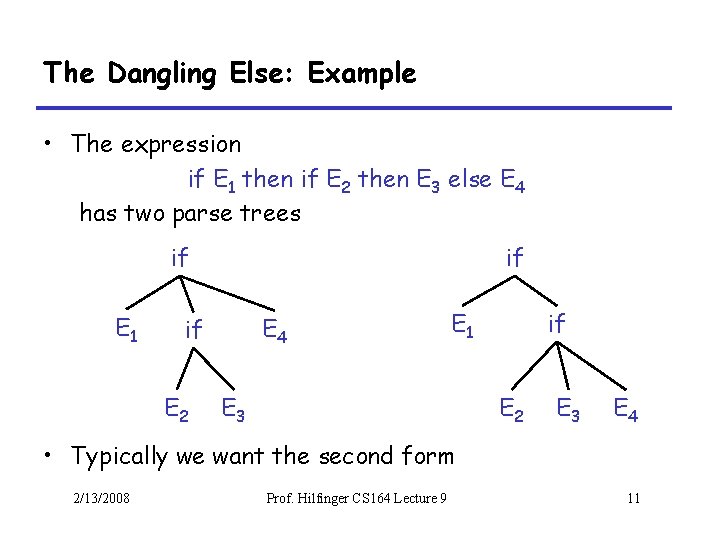
The Dangling Else: Example • The expression if E 1 then if E 2 then E 3 else E 4 has two parse trees if E 1 if E 4 if E 2 E 1 E 3 if E 2 E 3 E 4 • Typically we want the second form 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 11

The Dangling Else: A Fix • else matches the closest unmatched then • We can describe this in the grammar (distinguish between matched and unmatched “then”) E MIF | UIF /* all then are matched */ /* some then are unmatched */ MIF if E then MIF else MIF | OTHER UIF if E then E | if E then MIF else UIF • Describes the same set of strings 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 12
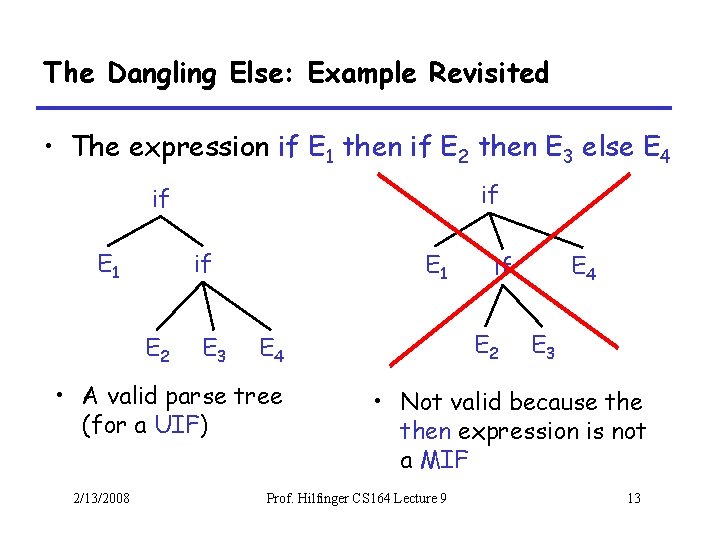
The Dangling Else: Example Revisited • The expression if E 1 then if E 2 then E 3 else E 4 if if E 1 if E 2 E 3 E 1 • A valid parse tree (for a UIF) 2/13/2008 E 2 E 4 if E 3 • Not valid because then expression is not a MIF Prof. Hilfinger CS 164 Lecture 9 13

Ambiguity • Impossible to convert automatically an ambiguous grammar to an unambiguous one • Used with care, ambiguity can simplify the grammar – Sometimes allows more natural definitions – But we need disambiguation mechanisms • Instead of rewriting the grammar – Use the more natural (ambiguous) grammar – Along with disambiguating declarations • Most tools allow precedence and associativity declarations to disambiguate grammars • Examples … 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 14

Associativity Declarations • Consider the grammar E E + E | int • Ambiguous: two parse trees of int + int E E E + E int int + E • Left-associativity declaration: %left ‘+’ 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 15
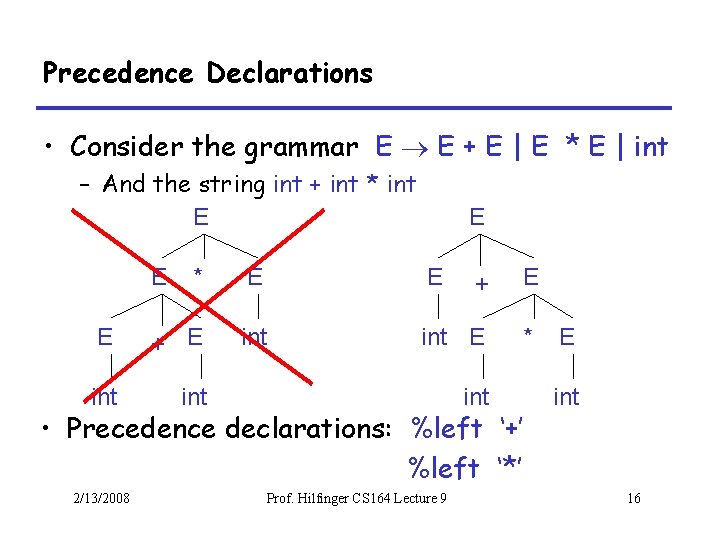
Precedence Declarations • Consider the grammar E E + E | E * E | int – And the string int + int * int E E E * E E + E int E * int int • Precedence declarations: %left ‘+’ %left ‘*’ 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 E int 16
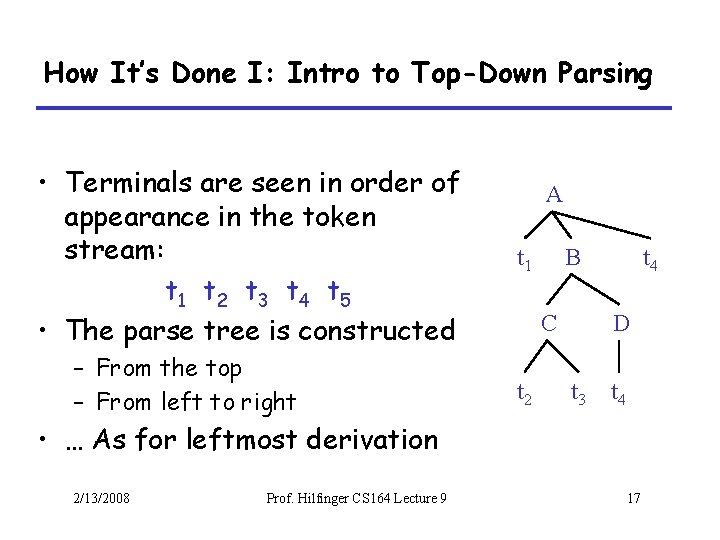
How It’s Done I: Intro to Top-Down Parsing • Terminals are seen in order of appearance in the token stream: t 1 t 2 t 3 t 4 t 5 • The parse tree is constructed – From the top – From left to right A t 1 B C t 2 t 4 D t 3 t 4 • … As for leftmost derivation 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 17

Top-down Depth-First Parsing • Consider the grammar E T+E|T T ( E ) | int * T • Token stream is: int * int • Start with top-level non-terminal E • Try the rules for E in order 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 18
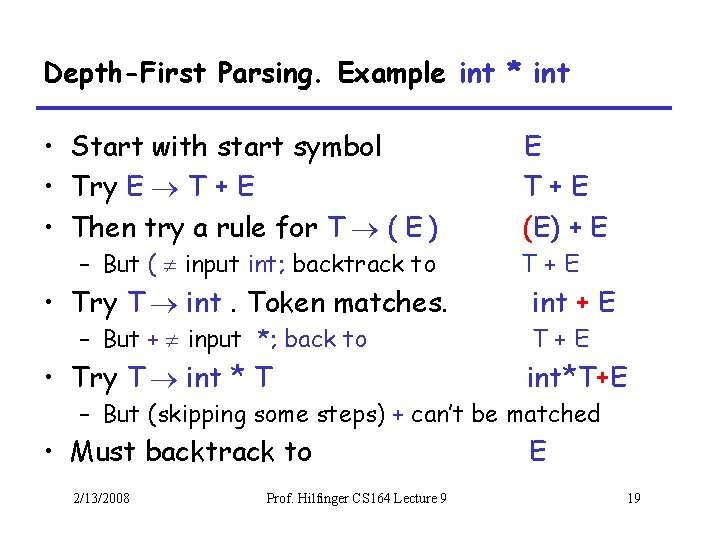
Depth-First Parsing. Example int * int • Start with start symbol • Try E T + E • Then try a rule for T ( E ) – But ( input int; backtrack to • Try T int. Token matches. – But + input *; back to • Try T int * T E T+E (E) + E T+E int*T+E – But (skipping some steps) + can’t be matched • Must backtrack to 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 E 19
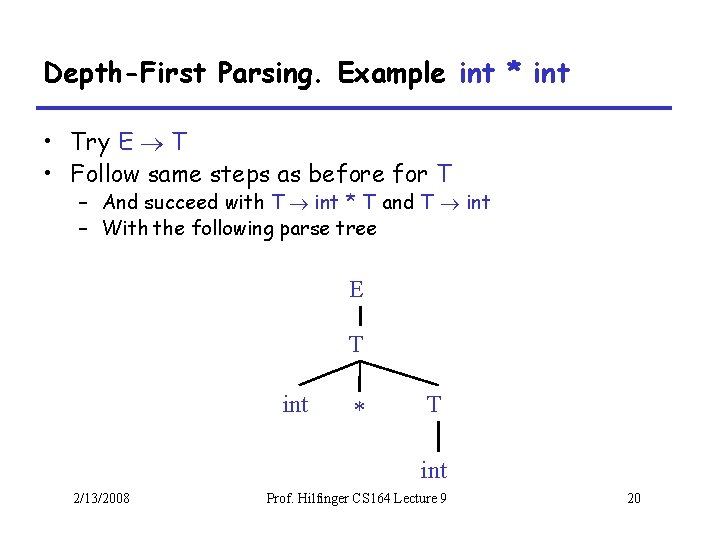
Depth-First Parsing. Example int * int • Try E T • Follow same steps as before for T – And succeed with T int * T and T int – With the following parse tree E T int * T int 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 20

Depth-First Parsing • Parsing: given a string of tokens t 1 t 2. . . tn, find a leftmost derivation (and thus, parse tree) • Depth-first parsing: Beginning with start symbol, try each production exhaustively on leftmost non-terminal in current sentential form and recurse. 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 21

Depth-First Parsing of t 1 t 2 … tn • At a given moment, have sentential form that looks like this: t 1 t 2 … tk A …, 0 k n • Initially, k=0 and A… is just start symbol • Try a production for A: if A BC is a production, the new form is t 1 t 2 … tk B C … • Backtrack when leading terminals aren’t prefix of t 1 t 2 … tn and try another production • Stop when no more non-terminals and terminals all matched (accept) or no more productions left (reject) 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 22

When Depth-First Doesn’t Work Well • Consider productions S S a | a: – In the process of parsing S we try the above rules – Applied consistently in this order, get infinite loop – Could re-order productions, but search will have lots of backtracking and general rule for ordering is complex • Problem here is left-recursive grammar: one that has a non-terminal S S + S for some 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 23

Elimination of Left Recursion • Consider the left-recursive grammar S S | • S generates all strings starting with a and followed by any number of ’s • Can rewrite using right-recursion S S’ S’ S’ | 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 24

Elimination of left Recursion. Example • Consider the grammar S 1 | S 0 ( = 1 and = 0 ) can be rewritten as S 1 S’ S’ 0 S’ | 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 25

More Elimination of Left Recursion • In general S S 1 | … | S n | 1 | … | m • All strings derived from S start with one of 1, …, m and continue with several instances of 1, …, n • Rewrite as S 1 S’ | … | m S’ S’ 1 S’ | … | n S’ | 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 26

General Left Recursion • The grammar S A | (1) A S (2) is also left-recursive because S + S • This left recursion can also be eliminated by first substituting (2) into (1) • There is a general algorithm (e. g. Aho, Sethi, Ullman § 4. 3) • But personally, I’d just do this by hand. 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 27

An Alternative Approach • Instead of reordering or rewriting grammar, can use top-down breadth-first search. S Sa|a String: aaa S Sa a (not all matched) Saa aa Saaa 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 28

Summary of Top-Down Parsing So Far • Simple and general parsing strategy – Left recursion must be eliminated first – … but that can be done automatically – Or can use breadth-first search • But backtracking (depth-first) or maintaining list of possible sentential forms (breadthfirst) can make it slow • Often, though, we can avoid both … 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 29

Predictive Parsers • Modification of depth-first parsing in which parser “predicts” which production to use – By looking at the next few tokens – No backtracking • Predictive parsers accept LL(k) grammars – L means “left-to-right” scan of input – L means “leftmost derivation” – k means “need k tokens of lookahead to predict” • In practice, LL(1) is used 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 30

Recursive Descent: Grammar as Program • In recursive descent, we think of a grammar as a program. Here, we’ll look at predictive version. • Each non-terminal is turned into a procedure • Each right-hand side transliterated into part of the procedure body for its non-terminal • First, define – next() current token of input – scan(t) check that next()=t (else ERROR), and then read new token. 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 31

Recursive Descent: Example P S$ S’ + S | S T S’ T int | ( S ) ($ = end marker) def P (): S(); scan($) def S(): T(); S’() predict def S’(): But where do if next() == ‘+’: scan(‘+’); S() prediction tests elif next() in [‘)’, $]: pass come from? else: �ERROR def T(): if next () == int: scan(int) elif next() == ‘(‘: scan(‘(‘); S(); scan (‘)’) else: ERROR 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 32

Predicting Right-hand Sides • The if-tests are conditions by which parser predicts which right-hand side to use. • In our example, used only next symbol (LL(1)); but could use more. • Can be specified as a 2 D table – One dimension for current non-terminal to expand – One dimension for next token – A table entry contains one production 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 33

But First: Left Factoring • With the grammar E T+E|T T int | int * T | ( E ) • Impossible to predict because – For T two productions start with int – For E it is not clear how to predict • A grammar must be left-factored before use for predictive parsing 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 34

Left-Factoring Example • Starting with the grammar E T+E|T T int | int * T | ( E ) • Factor out common prefixes of productions E TX X +E| T ( E ) | int Y Y *T| 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 35

Recursive Descent for Real • So far, have presented a purist view. • In fact, use of recursive descent makes life simpler in many ways if we “cheat” a bit. • Here’s how you really handle left recursion in recursive descent, for S S A | R: def S(): R () while next() FIRST(A): A() • It’s a program: all kinds of shortcuts possible. 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 36
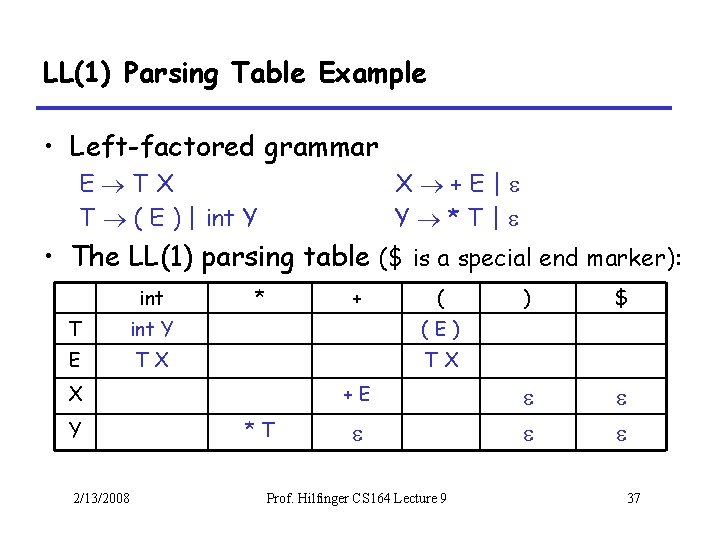
LL(1) Parsing Table Example • Left-factored grammar E TX T ( E ) | int Y X +E| Y *T| • The LL(1) parsing table ($ is a special end marker): int * + ( T int Y (E) E TX TX X Y 2/13/2008 +E *T Prof. Hilfinger CS 164 Lecture 9 ) $ 37
![LL(1) Parsing Table Example (Cont. ) • Consider the [E, int] entry – Means LL(1) Parsing Table Example (Cont. ) • Consider the [E, int] entry – Means](http://slidetodoc.com/presentation_image/06a12817a29285e163a6060200bcc7fc/image-38.jpg)
LL(1) Parsing Table Example (Cont. ) • Consider the [E, int] entry – Means “When current non-terminal is E and next input is int, use production E T X” – T X can generate string with int in front • Consider the [Y, +] entry – “When current non-terminal is Y and current token is +, get rid of Y” – We’ll see later why this is right 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 38

LL(1) Parsing Tables. Errors • Blank entries indicate error situations – Consider the [E, *] entry – “There is no way to derive a string starting with * from non-terminal E” 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 39

Using Parsing Tables • Essentially table-driven recursive descent, except – We use a stack to keep track of pending nonterminals • We reject when we encounter an error state • We accept when we encounter end-of-input 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 40

LL(1) Parsing Algorithm initialize stack = <S, $> repeat case stack of <X, rest> : if T[X, next()] == Y 1…Yn: stack <Y 1… Yn rest>; else: error (); <t, rest> : scan (t); stack <rest>; until stack == < > 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 41

LL(1) Parsing Example Stack E$ TX$ int Y X $ YX$ *TX$ int Y X $ YX$ X$ $ 2/13/2008 Input int * int $ * int $ $ Prof. Hilfinger CS 164 Lecture 9 Action TX int Y terminal *T terminal int Y terminal ACCEPT 42

Constructing Parsing Tables • LL(1) languages are those definable by a parsing table for the LL(1) algorithm such that no table entry is multiply defined • Once we have the table – Can create table-driver or recursive-descent parser – The parsing algorithms are simple and fast – No backtracking is necessary • We want to generate parsing tables from CFG 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 43
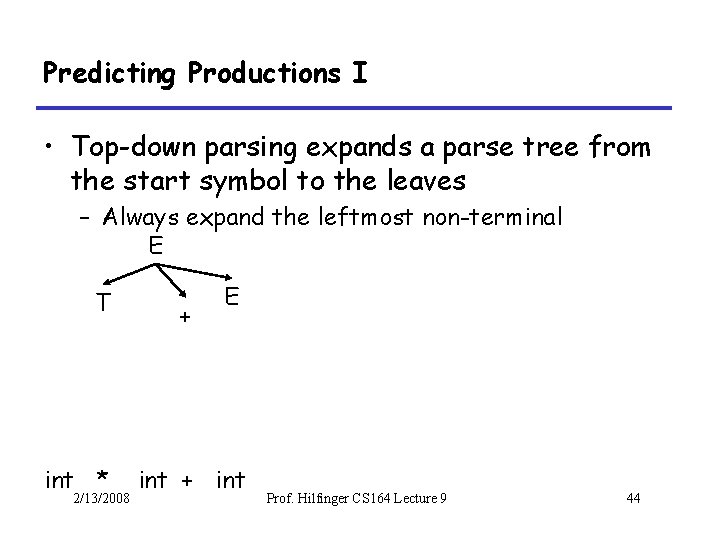
Predicting Productions I • Top-down parsing expands a parse tree from the start symbol to the leaves – Always expand the leftmost non-terminal E T int * 2/13/2008 + E int + int Prof. Hilfinger CS 164 Lecture 9 44
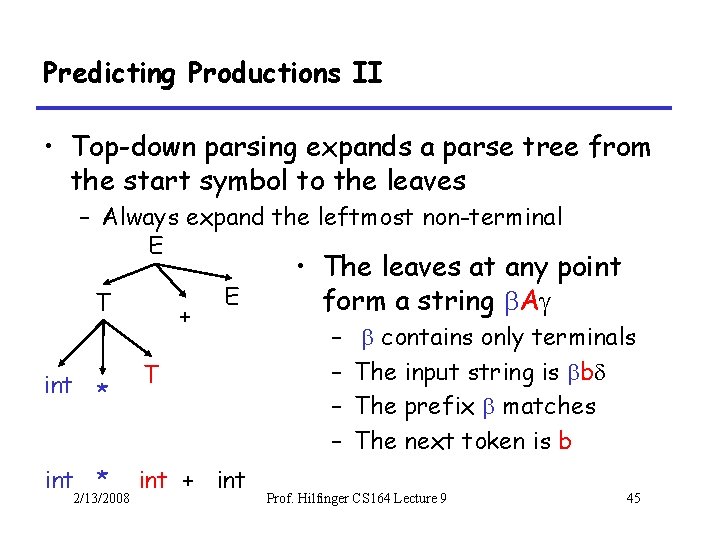
Predicting Productions II • Top-down parsing expands a parse tree from the start symbol to the leaves – Always expand the leftmost non-terminal E T + E int * T int * int + int 2/13/2008 • The leaves at any point form a string Ag – – contains only terminals The input string is b The prefix matches The next token is b Prof. Hilfinger CS 164 Lecture 9 45
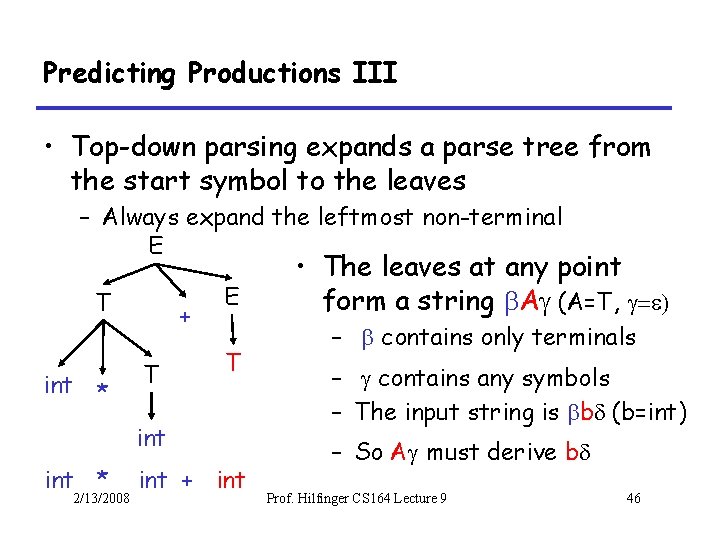
Predicting Productions III • Top-down parsing expands a parse tree from the start symbol to the leaves – Always expand the leftmost non-terminal E T int * + T E T int * 2/13/2008 int + int • The leaves at any point form a string Ag (A=T, g – contains only terminals – g contains any symbols – The input string is b (b=int) – So Ag must derive b Prof. Hilfinger CS 164 Lecture 9 46
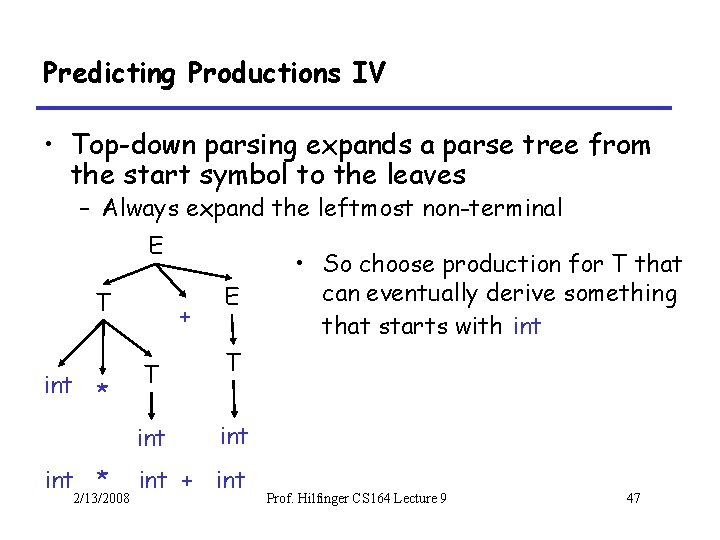
Predicting Productions IV • Top-down parsing expands a parse tree from the start symbol to the leaves – Always expand the leftmost non-terminal E T int * 2/13/2008 + E T T int int + int • So choose production for T that can eventually derive something that starts with int Prof. Hilfinger CS 164 Lecture 9 47

Predicting Productions V • Go back to previous grammar, with E TX T ( E ) | int Y E Here, YX must match + int T int 2/13/2008 X +E| Y *T| X Since + int doesn’t start with *, can’t use Y * T Y + int Prof. Hilfinger CS 164 Lecture 9 48
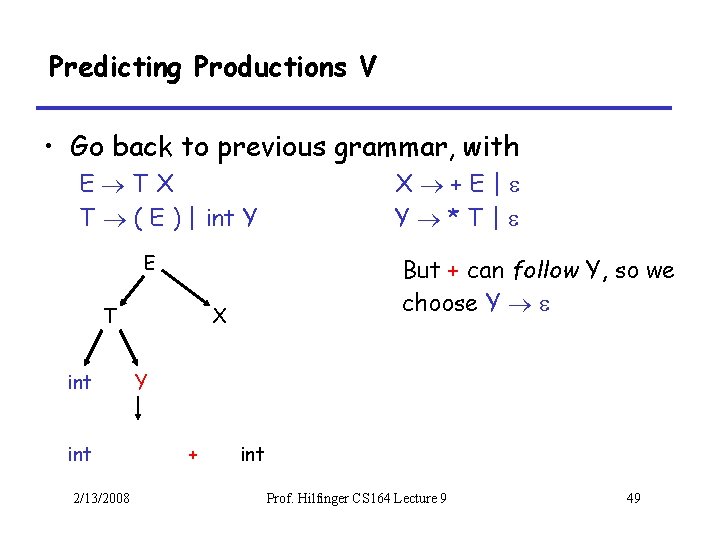
Predicting Productions V • Go back to previous grammar, with E TX T ( E ) | int Y E T int 2/13/2008 X +E| Y *T| But + can follow Y, so we choose Y X Y + int Prof. Hilfinger CS 164 Lecture 9 49

FIRST and FOLLOW • To summarize, if we are trying to predict how to expand A with b the next token, then either: – b belongs to an expansion of A • Any A can be used if b can start a string derived from • – In this case we say that b First( ) or b does not belong to an expansion of A, A has an expansion that derives , and b belongs to something that can follow A (so S * Ab ) • 2/13/2008 We say that b Follow(A) in this case. Prof. Hilfinger CS 164 Lecture 9 50

Summary of Definitions • For b T, the set of terminals; a sequence of terminal & non-terminal symbols, S the start symbol, A N, the set of non-terminals: • FIRST( ) T { } b FIRST( ) iff * b … FIRST( ) iff * • FOLLOW(A) T b FOLLOW(A) iff S * … A b … 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 51

Computing First Sets Definition First(X) = { b | X * b } { | X * }, X any grammar symbol. 1. First(b) = { b } for b any terminal symbol 2. For all productions X A 1 … An • 1. 2. 3. 4. Add First(A 1) – { } to First(X). Stop if First(A 1) Add First(A 2) – { } to First(X). Stop if First(A 2) … Add First(An) – { } to First(X). Stop if First(An) Add to First(X) 3. Repeat 2 until nothing changes (“compute fixed point”) 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 52

Computing First Sets, Contd. • That takes care of single-symbol case. • In general: FIRST(X 1 X 2…Xk) = FIRST(X 1) FIRST(X 2) if FIRST(X 1) … FIRST(Xk) if FIRST(X 1 X 2…Xk-1) - { } unless FIRST(Xi) i 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 53

First Sets. Example • For the grammar E TX T ( E ) | int Y • First sets First( ( ) = { ( } First( ) ) = { ) } First( int) = { int } First( + ) = { + } First( * ) = { * } 2/13/2008 X +E| Y *T| First( T ) = {int, ( } First( E ) = {int, ( } First( X ) = {+, } First( Y ) = {*, } Prof. Hilfinger CS 164 Lecture 9 54

Computing Follow Sets Definition Follow(X) = { b | S * X b } 1. Compute the First sets for all non-terminals first 2. Add $ to Follow(S) (if S is the start non-terminal) 3. For all productions Y … X A 1 … An 1. 2. 3. 4. 5. Add First(A 1) – { } to Follow(X). Stop if First(A 1) Add First(A 2) – { } to Follow(X). Stop if First(A 2) … Add First(An) – { } to Follow(X). Stop if First(An) Add Follow(Y) to Follow(X) 4. Repeat 3 until nothing changes. 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 55

Follow Sets. Example • For the grammar E TX T ( E ) | int Y X +E| Y *T| • Follow sets Follow( E ) = {), $} Follow( X ) = {$, ) } Follow( Y ) = {+, ) , $} Follow( T ) = {+, ) , $} 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 56

Constructing LL(1) Parsing Tables • Construct a parsing table T for CFG G • For each production A in G do: – For each terminal b First( ) do • T[A, b] = – If * , for each b Follow(A) do • T[A, b] = 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 57
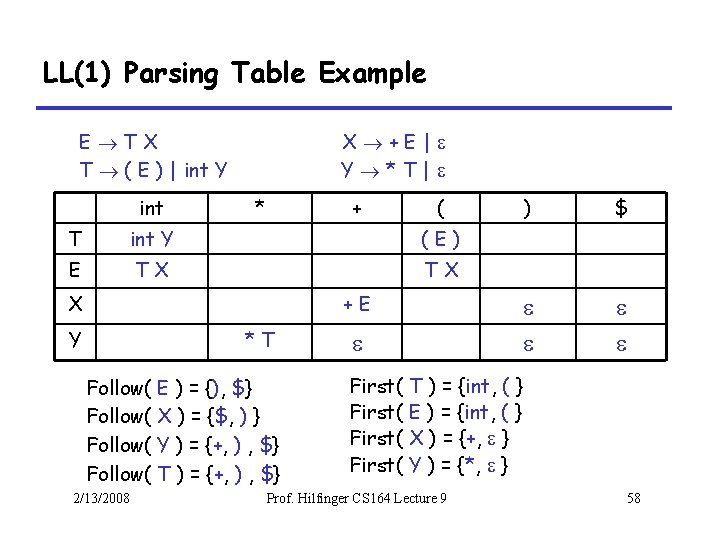
LL(1) Parsing Table Example E TX T ( E ) | int Y int X +E| Y *T| * + ( T int Y (E) E TX TX X +E Y *T Follow( 2/13/2008 E ) = {), $} X ) = {$, ) } Y ) = {+, ) , $} T ) = {+, ) , $} First( ) $ T ) = {int, ( } E ) = {int, ( } X ) = {+, } Y ) = {*, } Prof. Hilfinger CS 164 Lecture 9 58

Notes on LL(1) Parsing Tables • If any entry is multiply defined then G is not LL(1). This happens – – If G is ambiguous If G is left recursive If G is not left-factored And in other cases as well • Most programming language grammars are not LL(1) • There are tools that build LL(1) tables 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 59

Review • For some grammars there is a simple parsing strategy – Predictive parsing (LL(1)) – Once you build the LL(1) table (or know the FIRST and FOLLOW sets), you can write the parser by hand: recursive descent. • Next: a more powerful parsing strategy for grammars that are not LL(1) 2/13/2008 Prof. Hilfinger CS 164 Lecture 9 60
- Slides: 60