ALU Unidad aritmticolgica Modelo de von Neumann Fuente

ALU Unidad aritmético-lógica

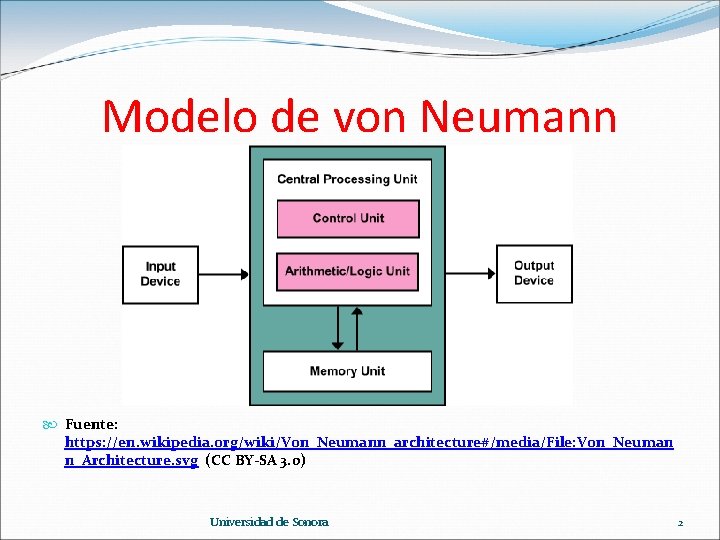
Modelo de von Neumann Fuente: https: //en. wikipedia. org/wiki/Von_Neumann_architecture#/media/File: Von_Neuman n_Architecture. svg (CC BY-SA 3. 0) Universidad de Sonora 2

Definición La ALU (unidad aritmético-lógica) es el dispositivo que se encarga de realizar: a) Operaciones aritméticas (suma, resta, etc. ). b) Operaciones lógicas (and, or, xor, etc. ). Universidad de Sonora Arquitectura de Computadoras 3

Circuitos combinatorios Su salida depende exclusivamente de sus entradas. Universidad de Sonora Arquitectura de Computadoras 4

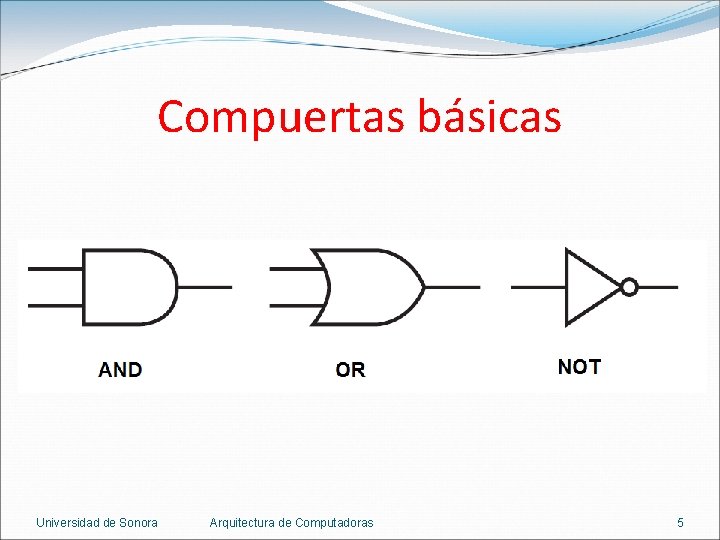
Compuertas básicas Universidad de Sonora Arquitectura de Computadoras 5

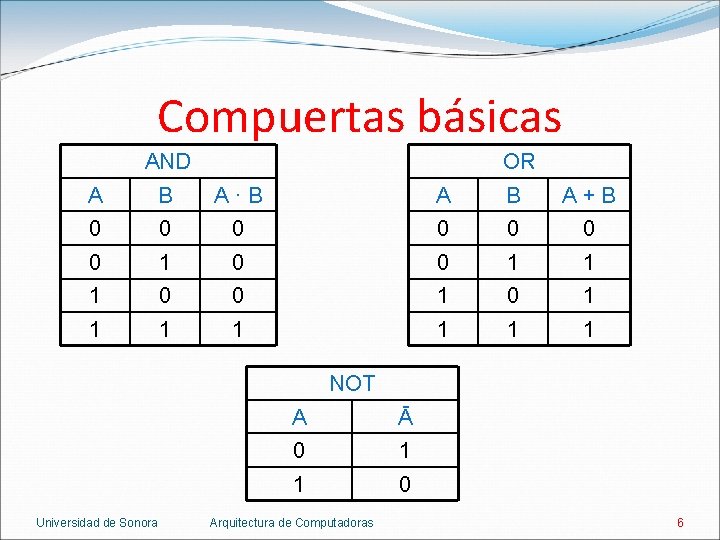
Compuertas básicas AND OR A B A·B A B A+B 0 0 0 0 1 1 1 0 0 1 1 1 1 NOT Universidad de Sonora A Ā 0 1 1 0 Arquitectura de Computadoras 6

Otras compuertas XOR (or exclusiv 0). EQV (equivalence). NAND (not AND). NOR (not OR). Universidad de Sonora Arquitectura de Computadoras 7

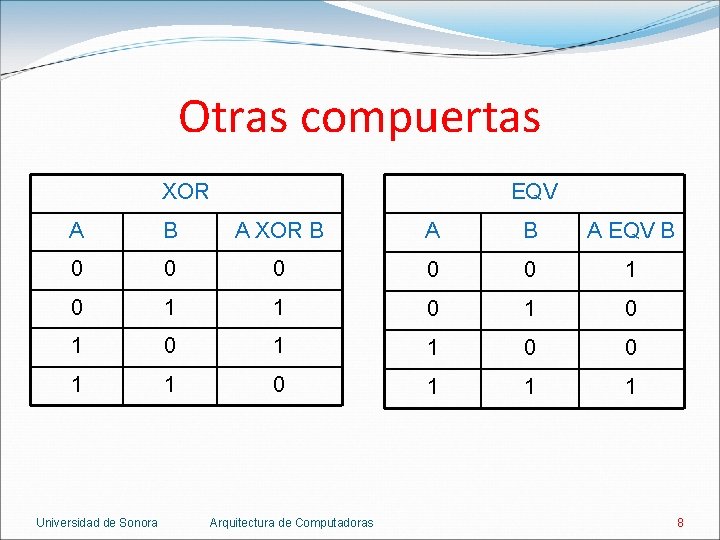
Otras compuertas XOR EQV A B A XOR B A EQV B 0 0 0 1 1 0 1 1 1 Universidad de Sonora Arquitectura de Computadoras 8

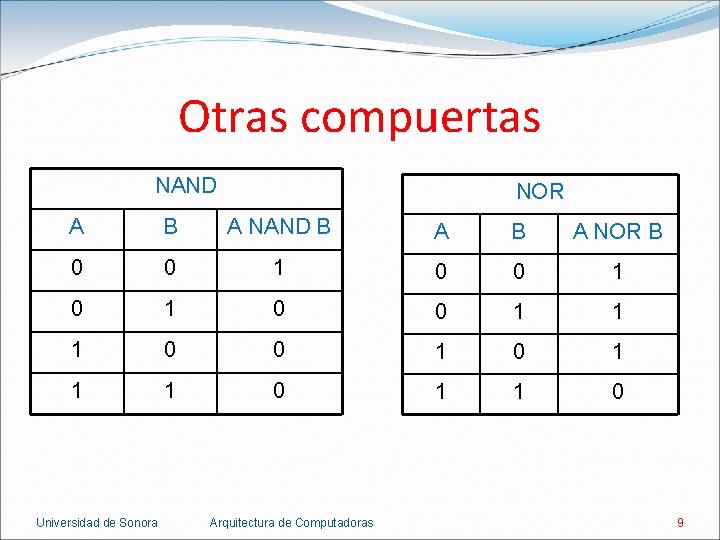
Otras compuertas NAND NOR A B A NAND B A NOR B 0 0 1 0 1 0 0 1 1 1 0 Universidad de Sonora Arquitectura de Computadoras 9

Multiplexor El multiplexor (mux) tiene 2 n entradas de datos, n bits de selección y una salida. Los bits de selección se usan para decidir cuál entrada pasa a la salida. Mux 2 a 1 Universidad de Sonora Arquitectura de Computadoras 10

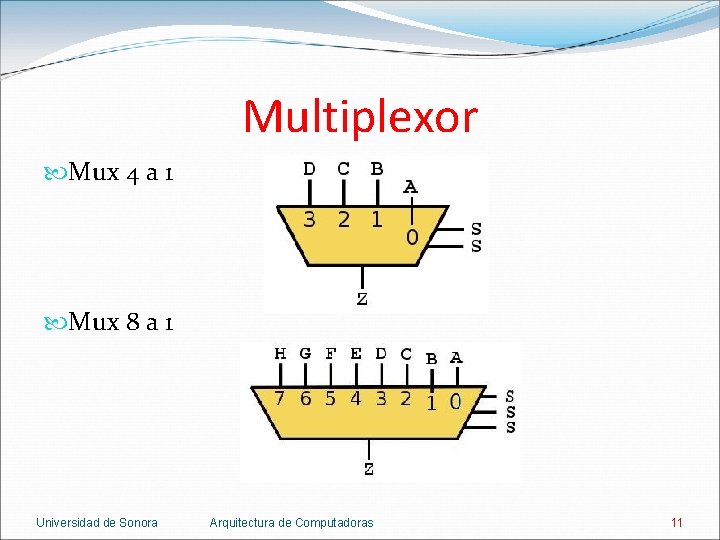
Multiplexor Mux 4 a 1 Mux 8 a 1 Universidad de Sonora Arquitectura de Computadoras 11

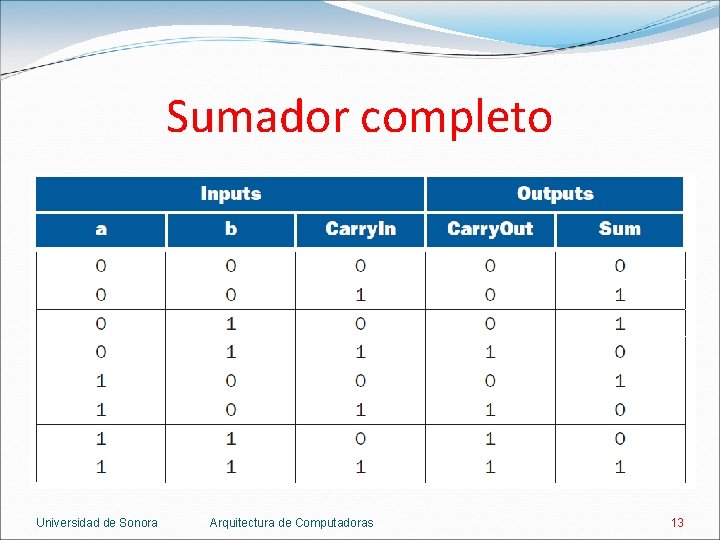
Sumador completo (full adder) de 1 bit: Entradas: dos números de 1 bit y un bit de carry de entrada. Salidas: la suma de 1 bit y un bit de carry de salida. Universidad de Sonora Arquitectura de Computadoras 12

Sumador completo Universidad de Sonora Arquitectura de Computadoras 13

Sumador completo Suma = a b Carry. In Carry. Out = (a · Carry. In) + (b · Carry. In) + (a · b) = (a + b) · Carry. In + (a · b) Universidad de Sonora Arquitectura de Computadoras 14

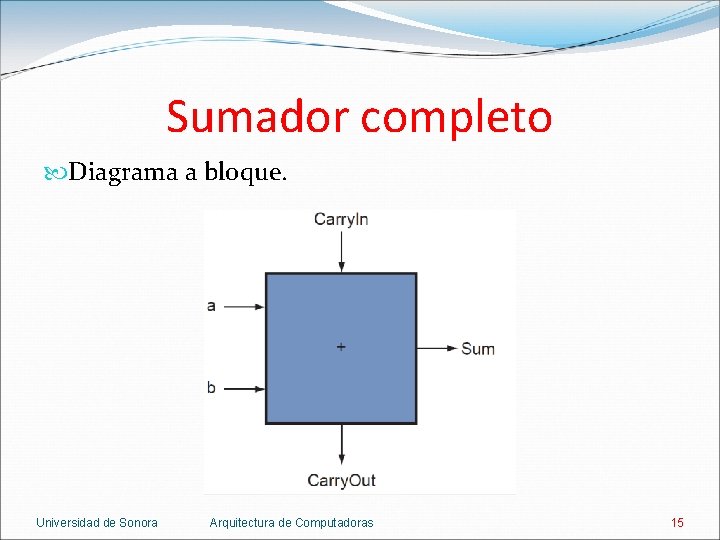
Sumador completo Diagrama a bloque. Universidad de Sonora Arquitectura de Computadoras 15

ALU de 1 bit Dos operaciones: AND y OR. Un bit para seleccionar la operación. Universidad de Sonora Arquitectura de Computadoras Operación Salida 0 a·b 1 a+b 16

Agregando operaciones El siguiente paso es agregar la suma. Se agrega un sumador completo al diseño anterior. Universidad de Sonora Arquitectura de Computadoras 17

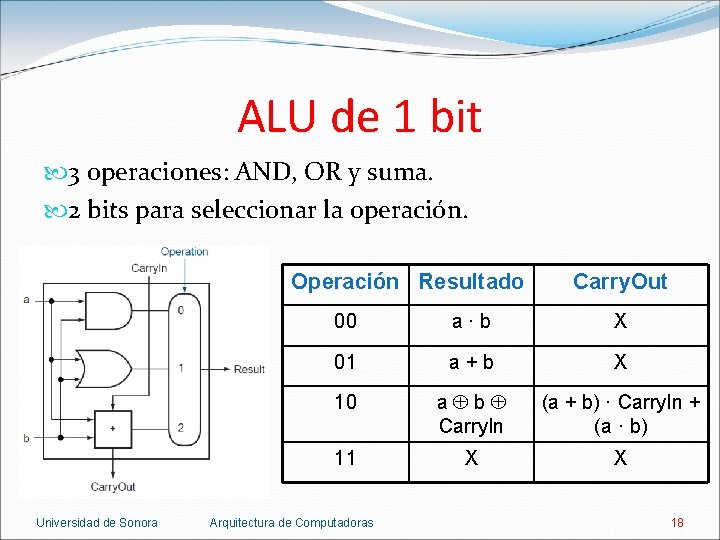
ALU de 1 bit 3 operaciones: AND, OR y suma. 2 bits para seleccionar la operación. Operación Resultado Universidad de Sonora Carry. Out 00 a·b X 01 a+b X 10 a b Carry. In (a + b) · Carry. In + (a · b) 11 X X Arquitectura de Computadoras 18

Agregando operaciones Agregar la resta a – b a + b si b está en complemento a 2. El complemento a dos de b se encuentra sumando 1 al complemento a uno de b. El complemento a uno de b se encuentra negando a b. a – b = a + (–b) = a + (¬b + 1) = a + ¬b + 1 El 1 de la suma viene en Carry. In. Universidad de Sonora Arquitectura de Computadoras 19

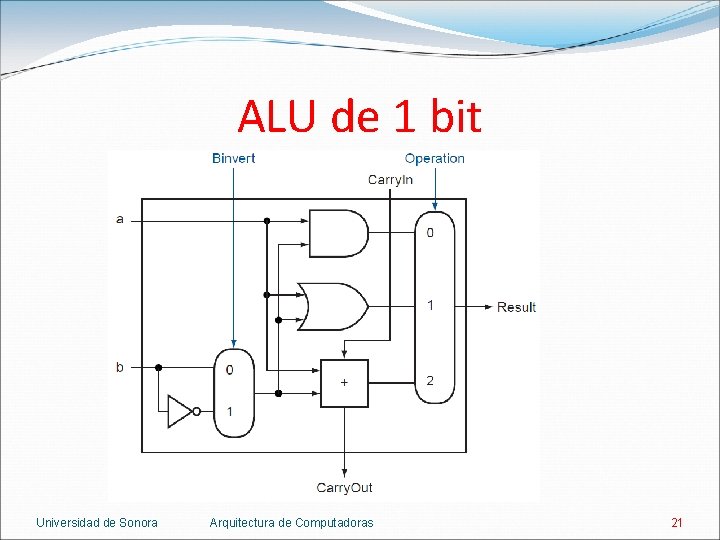
ALU de 1 bit 4 operaciones: AND, OR, suma y resta. 2 bits para seleccionar la operación. Un bit extra para diferenciar entre la suma y la resta. En la resta, Carry. In es 1. Universidad de Sonora Arquitectura de Computadoras 20

ALU de 1 bit Universidad de Sonora Arquitectura de Computadoras 21

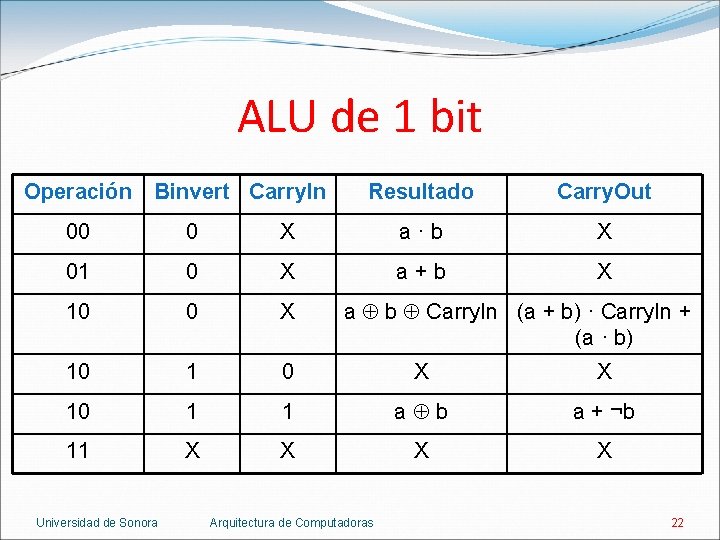
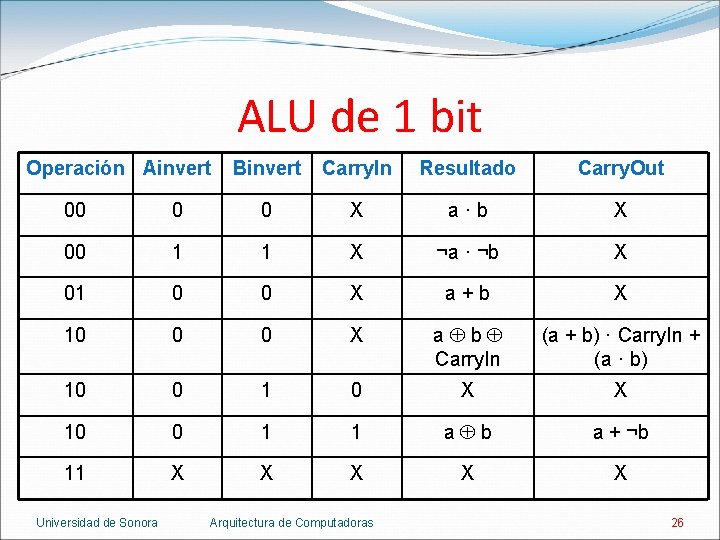
ALU de 1 bit Operación Binvert Carry. In Resultado Carry. Out 00 0 X a·b X 01 0 X a+b X 10 0 X 10 1 0 X X 10 1 1 a b a + ¬b 11 X X Universidad de Sonora a b Carry. In (a + b) · Carry. In + (a · b) Arquitectura de Computadoras 22

Agregando operaciones Agregar la operación NOR: ¬(a + b) Ley de De. Morgan: ¬(a + b) = ¬a · ¬b La ALU ya puede calcular a · b y ¬b. Hace falta poder calcular ¬a. Universidad de Sonora Arquitectura de Computadoras 23

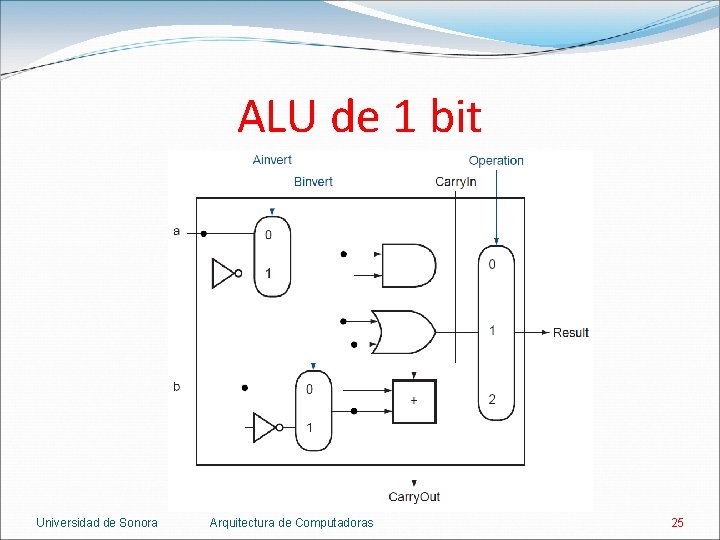
ALU de 1 bit 5 operaciones: AND, OR, NOR, suma y resta. 2 bits para seleccionar la operación. Binvert diferencia entre la suma y la resta. En la resta, Carry. In es 1. Ainvert y Binvert diferencian entre AND y NOR. Universidad de Sonora Arquitectura de Computadoras 24

ALU de 1 bit Universidad de Sonora Arquitectura de Computadoras 25

ALU de 1 bit Operación Ainvert Binvert Carry. In Resultado Carry. Out 00 0 0 X a·b X 00 1 1 X ¬a · ¬b X 01 0 0 X a+b X 10 0 0 X a b Carry. In (a + b) · Carry. In + (a · b) 10 0 1 0 X X 10 0 1 1 a b a + ¬b 11 X X X Universidad de Sonora Arquitectura de Computadoras 26

Agregando operaciones Variando Ainvert y Binvert permite generar: 8 operaciones lógicas. 5 operaciones aritméticas. Universidad de Sonora Arquitectura de Computadoras 27

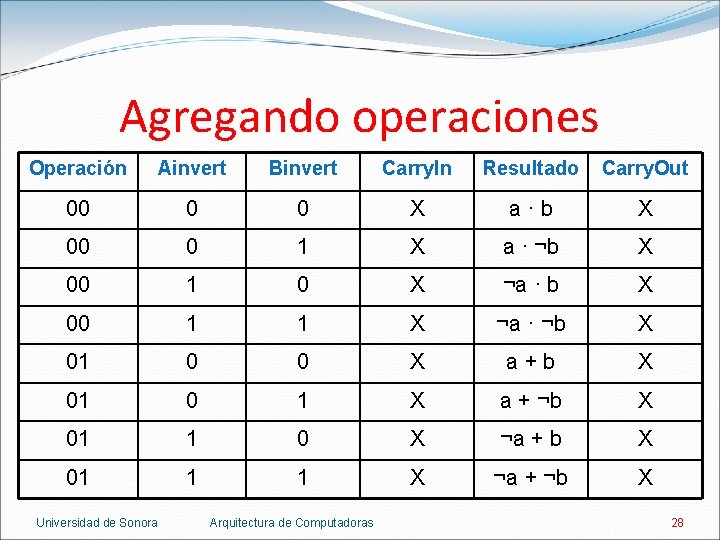
Agregando operaciones Operación Ainvert Binvert Carry. In Resultado Carry. Out 00 0 0 X a·b X 00 0 1 X a · ¬b X 00 1 0 X ¬a · b X 00 1 1 X ¬a · ¬b X 01 0 0 X a+b X 01 0 1 X a + ¬b X 01 1 0 X ¬a + b X 01 1 1 X ¬a + ¬b X Universidad de Sonora Arquitectura de Computadoras 28

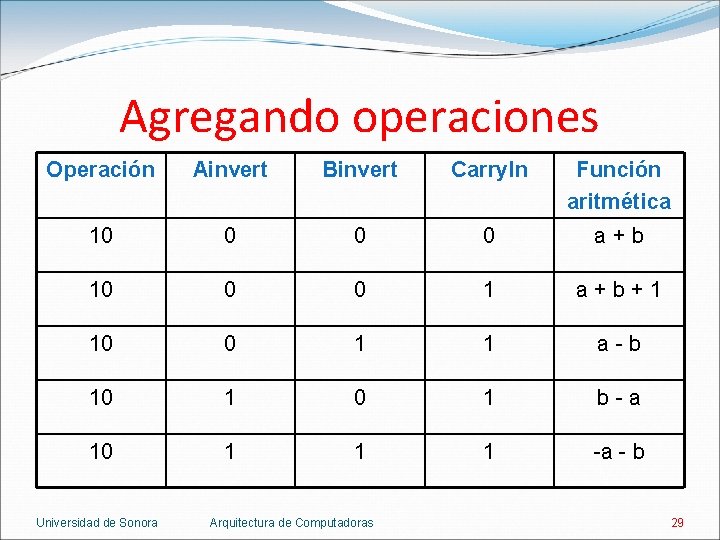
Agregando operaciones Operación Ainvert Binvert Carry. In Función aritmética 10 0 a+b 10 0 0 1 a+b+1 10 0 1 1 a-b 10 1 b-a 10 1 1 1 -a - b Universidad de Sonora Arquitectura de Computadoras 29

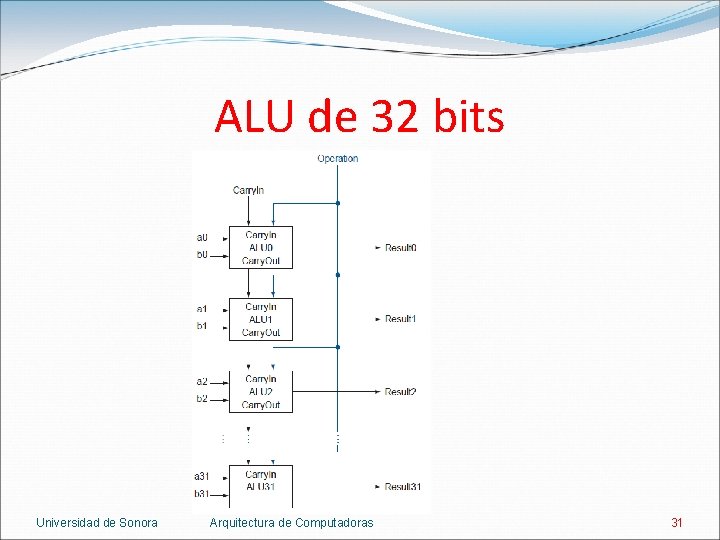
ALU de 32 bits ¿Cómo se genera una ALU de 32 bits? Con 32 ALUs de 1 bit. Carry. Out de la ALUi se conecta a Carry. In de la ALUi+1. En la resta Carry. In ALU 0 se conecta a 1. Universidad de Sonora Arquitectura de Computadoras 30

ALU de 32 bits Universidad de Sonora Arquitectura de Computadoras 31

ALU para MIPS El diseño de la ALU está incompleto. La mayoría de las instrucciones de MIPS pueden ser realizadas con las operaciones AND, OR, suma y resta. Se necesita soportar la instrucción slt (set on less than). slt $x, $y, $z guarda uno en $x si $y < $z o cero en otro caso. Universidad de Sonora Arquitectura de Computadoras 32

Soportando slt $x, $y, $z pone a ceros los bits 1 a 31 de $x. El bit cero de $x tiene el resultado de la comparación de $y y $z. $x Universidad de Sonora 0 0 … 31 30 … Arquitectura de Computadoras 0 1 $y < $z 0 33

Soportando slt Se calcula t = $y - $z. Si t es negativo $y < $z. Si t es positivo o cero $y $z. En MIPS los números negativos tienen 1 en el bit 31. El bit 31 de t tiene el resultado de la comparación. Universidad de Sonora Arquitectura de Computadoras 34

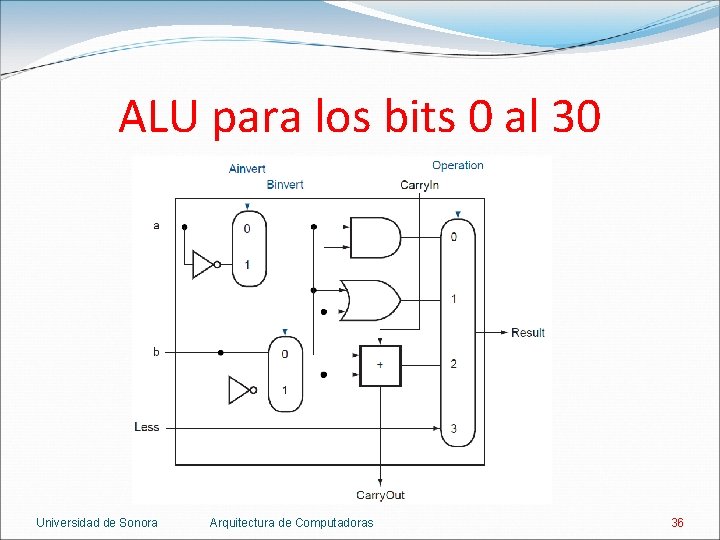
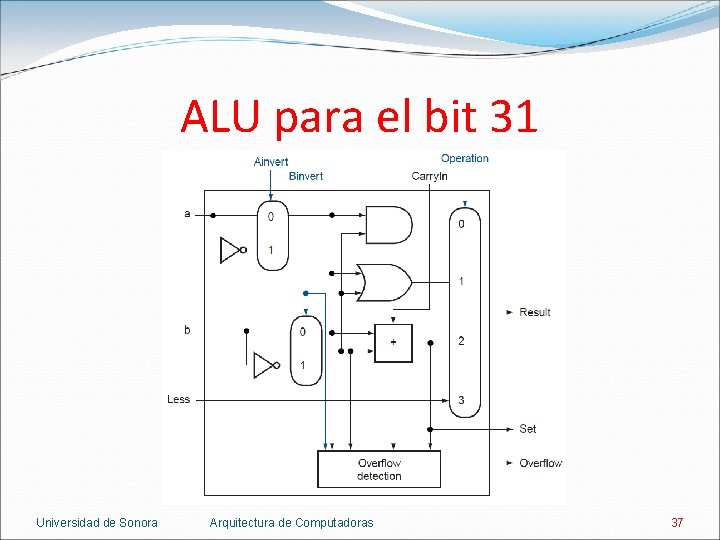
Soportando slt Para hacer una ALU de 32 bits se consideran dos tipos de ALU distintos. Una para los bits del 0 al 30. Parecida al diseño anterior, tiene una entrada extra llamada Less. Otra para el bit 31. Además de la entrada Less, tiene una salida Set con el signo de la resta y un detector de overflow. Universidad de Sonora Arquitectura de Computadoras 35

ALU para los bits 0 al 30 Universidad de Sonora Arquitectura de Computadoras 36

ALU para el bit 31 Universidad de Sonora Arquitectura de Computadoras 37

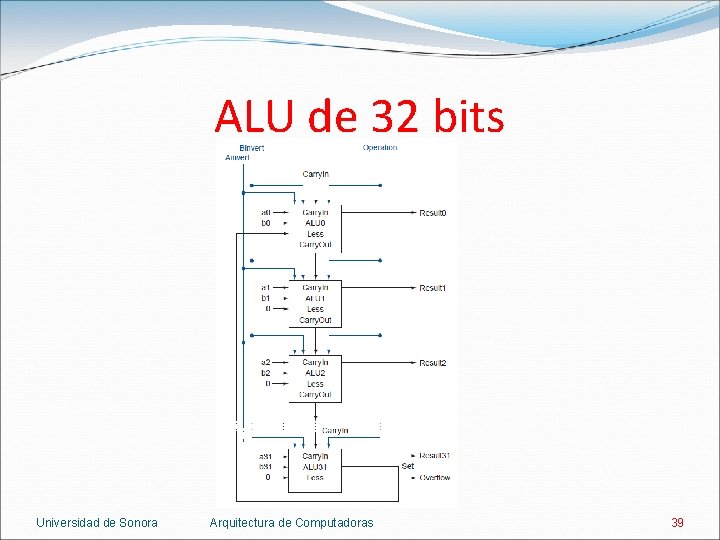
ALU de 32 bits Se conectan las 32 ALUs. Carry. Out de la ALUi se conecta a Carry. In de la ALUi+1. Las entradas Less de la ALU 1 a la ALU 31 se ponen a 0. La entrada Less de la ALU 0 se conecta a la salida Set de la ALU 31. En la resta Carry. In de la ALU 0 se conecta a 1. Universidad de Sonora Arquitectura de Computadoras 38

ALU de 32 bits Universidad de Sonora Arquitectura de Computadoras 39

ALU para MIPS Falta soportar los brincos condicionales. beq $x, $y, L – brinca a L si $x = $y. bne $x, $y, L – brinca a L si $x $y. Se calcula t = $x - $y. Si t es cero, $x = $y. Si t no es cero, $x $y. Universidad de Sonora Arquitectura de Computadoras 40

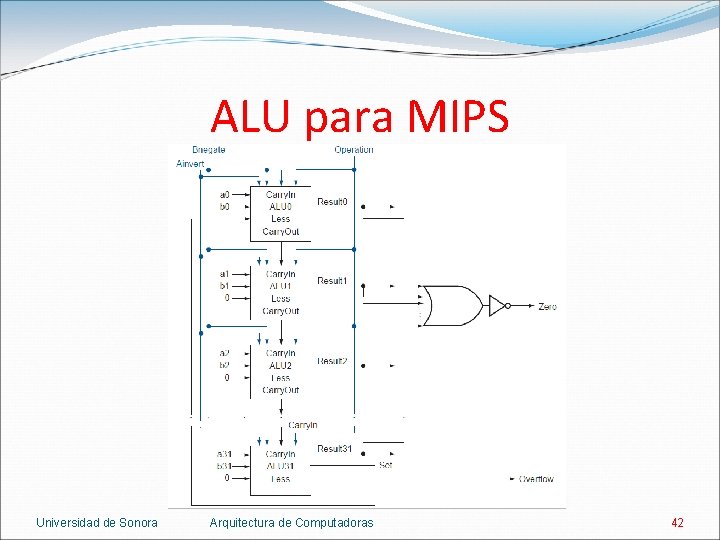
ALU para MIPS Se agrega una salida Zero que detecte cuando todos los bits de resultado sean cero. Zero = ¬(Result 31 + Result 30 + … + Result 1 + Result 0) Se combinan la entradas Binvert y Carry. In de la ALU 0 con el nombre Bnegate. Binvert = Carry. In = 1 cuando hay que restar. Binvert = Carry. In = 0 en la suma y operaciones lógicas. Universidad de Sonora Arquitectura de Computadoras 41

ALU para MIPS Universidad de Sonora Arquitectura de Computadoras 42

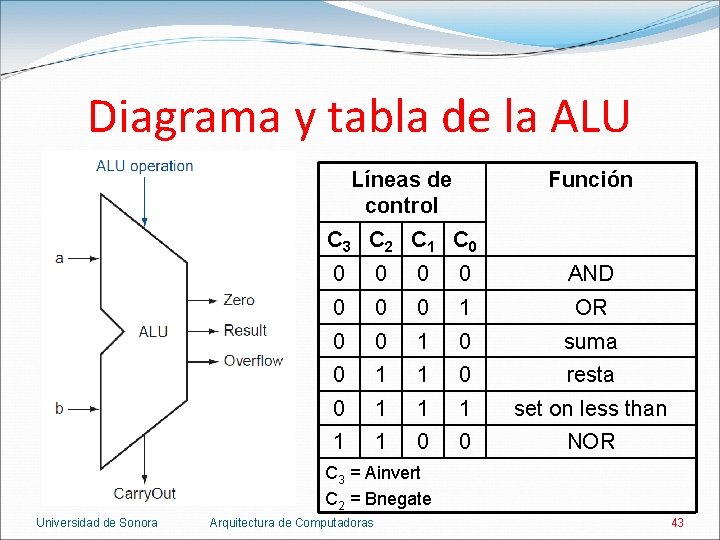
Diagrama y tabla de la ALU Líneas de control Función C 3 C 2 C 1 C 0 0 0 AND 0 0 0 1 OR 0 0 1 0 suma 0 1 1 0 resta 0 1 1 1 set on less than 1 1 0 0 NOR C 3 = Ainvert C 2 = Bnegate Universidad de Sonora Arquitectura de Computadoras 43

Overflow en MIPS El overflow se presenta cuando el resultado de una operación no se puede representar con 32 bits. En MIPS hay dos clases de instrucciones aritméticas: una para enteros con signo y otra para enteros sin signo. 1. La suma (add), suma inmediata (addi) y resta (sub), reconocen el overflow. 2. La suma sin signo (addu), suma inmediata sin signo (addiu) y resta sin signo (subu), ignoran el overflow. Universidad de Sonora Arquitectura de Computadoras 44