ALTERNATIVES LOTSIZING SCHEMES Alternatives LotSizing Schemes The silvermeal

ALTERNATIVES LOT-SIZING SCHEMES

Alternatives Lot-Sizing Schemes • The silver-meal heuristic • Least Unit Cost • Past Period Balancing

The Silver-Meal Heuristic • Forward method that requires determining the average cost period as a function of the number of periods the current order to span. • Minimize the cost period • Formula : C(j) = (K + hr 2 + 2 hr 3 + … + (j-1)hrj) / j • C(j) average holding cost and setup cost period • k order cost or setup cost • h holding cost • r demand

Method I. Start the calculation from period 1 to next period § § § C(1) = K C(2) = (K + hr 2) / 2 C(3) = (K + hr 2 + 2 hr 3) / 3 II. Stop the calculation when C(j) > C(j-1) III. Set y 1 = r 1 + r 2 + … + rj-1 IV. Start over at period j, repeat step (I) – (III)

Example • A machine shop uses the Silver-Meal heuristic to schedule production lot sizes for computer casings. Over the next five weeks the demands for the casing are r = (18, 30, 42, 5, 20). The holding cost is $2 per case per week, and the production setup cost is $80. Find the recommended lot sizing.

Step I, II & III r = (18, 30, 42, 5, 20) k = $80 h = $2 Starting in period 1 • C(1) = 80 • C(2) = [80 + (2)(30)] / 2 = 70 • C(3) = [80 + (2)(30) + (2)(2)(42)] / 3 = 102. 67 Stop the calculation as the C(3) > C(2) • y 1 = r 1 + r 2 = 18 +30 = 48

Step IV Starting in period 3 • C(1) = 80 • C(2) = [80 + (2)(5)] / 2 = 45 • C(3) = [80 + (2)(5) + (2)(2)(20)] / 3 = 56. 67. Stop • y 3 = r 3 + r 4 = 42 + 5 = 47

• Since period 5 is the final period, thus no need to start the process again. • Set y 5 = r 5 = 20 • Thus y = (48, 0, 47, 0, 20)

Least Unit Cost • Similar to Silver-Meal method • Minimize cost per unit of demand • Formula : C(j) = (K + hr 2 + 2 hr 3 + … + (j-1)hrj) / (r 1 + r 2 + … + rj • C(j) average holding cost and setup cost period • k order cost or setup cost • h holding cost • r demand

Method I. Start the calculation from period 1 to next period § § § C(1) = K / r 1 C(2) = (K + hr 2) / (r 1 + r 2) C(3) = (K + hr 2 + 2 hr 3) / (r 1 + r 2 + r 3 ) II. Stop the calculation when C(j) > C(j-1) III. Set y 1 = r 1 + r 2 + … + rj-1 IV. Start over at period j, repeat step (I) – (III)

Step I, II & III r = (18, 30, 42, 5, 20) k = $80 h = $2 Starting in period 1 • C(1) = 80 / 18 = 4. 44 • C(2) = [80 + (2)(30)] / (18 + 30) = 2. 92 • C(3) = [80 + (2)(30) + (2)(2)(42)] / (18+30+42) = 3. 42 Stop the calculation as the C(3) > C(2) • y 1 = r 1 + r 2 = 18 +30 = 48

Step IV • Starting in period 3 • C(1) = 80 / 42 = 1. 9 • C(2) = [80 + (2)(5)] / (42 + 5) = 1. 92 Stop • y 3 = r 3 = 42

Step IV Starting in period 4 • C(1) = 80 / 5 = 16 • C(2) = [80 + (2)(20)] / (5 + 20) = 4. 8 • y 4 = r 4 + r 5 = 5 + 20 = 25 • Thus y = (48, 0, 42, 25, 0)

Part Period Balancing • Set the order horizon equal to the number of periods that most closely matches the total holding cost with the setup cost over that period.

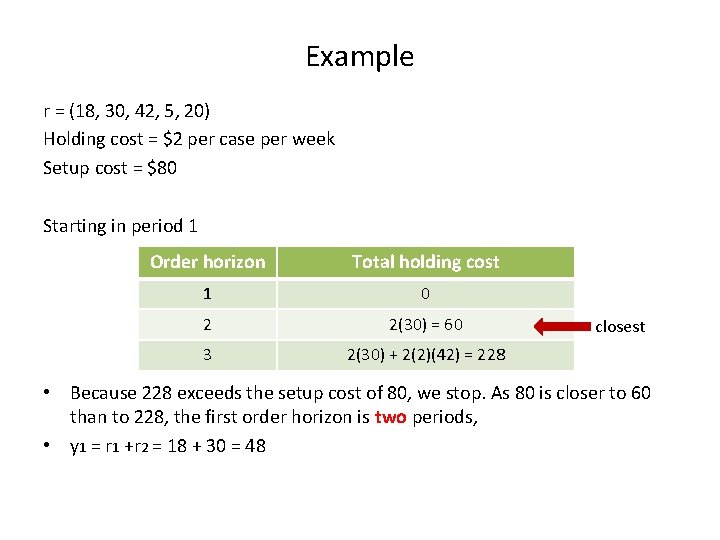
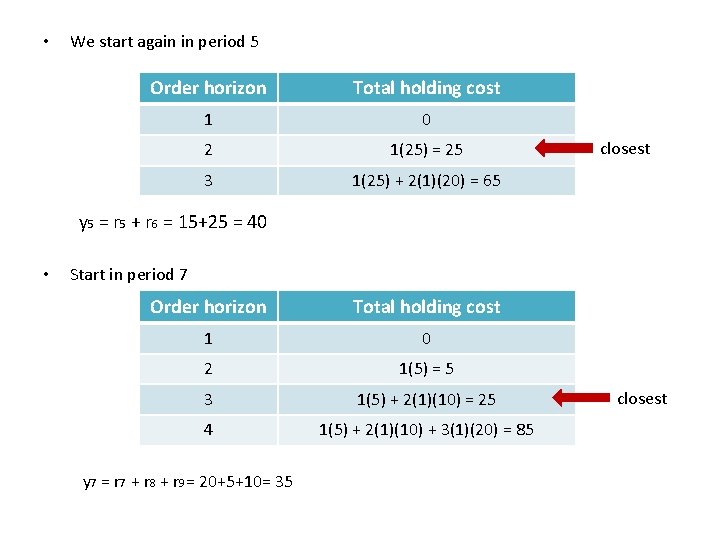
Example r = (18, 30, 42, 5, 20) Holding cost = $2 per case per week Setup cost = $80 Starting in period 1 Order horizon Total holding cost 1 0 2 2(30) = 60 3 2(30) + 2(2)(42) = 228 closest • Because 228 exceeds the setup cost of 80, we stop. As 80 is closer to 60 than to 228, the first order horizon is two periods, • y 1 = r 1 +r 2 = 18 + 30 = 48

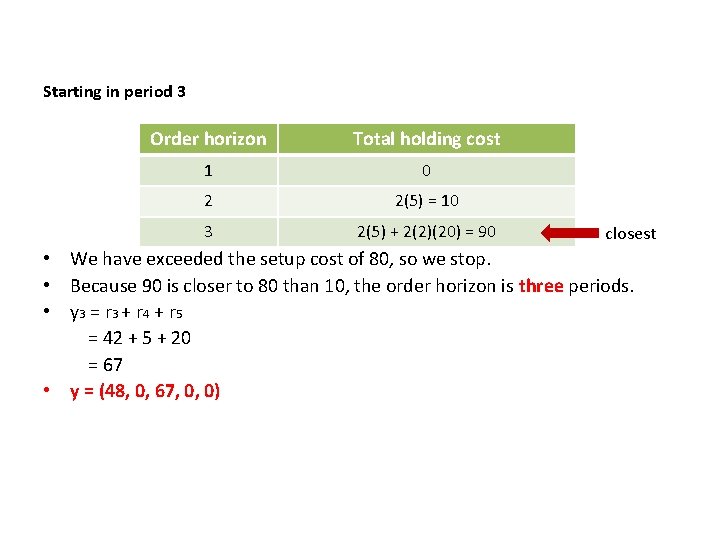
Starting in period 3 Order horizon Total holding cost 1 0 2 2(5) = 10 3 2(5) + 2(2)(20) = 90 closest • We have exceeded the setup cost of 80, so we stop. • Because 90 is closer to 80 than 10, the order horizon is three periods. • y 3 = r 3 + r 4 + r 5 = 42 + 5 + 20 = 67 • y = (48, 0, 67, 0, 0)

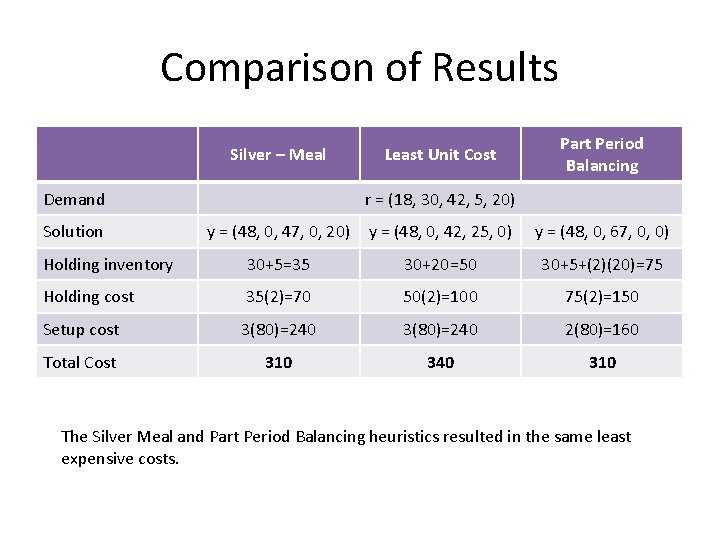
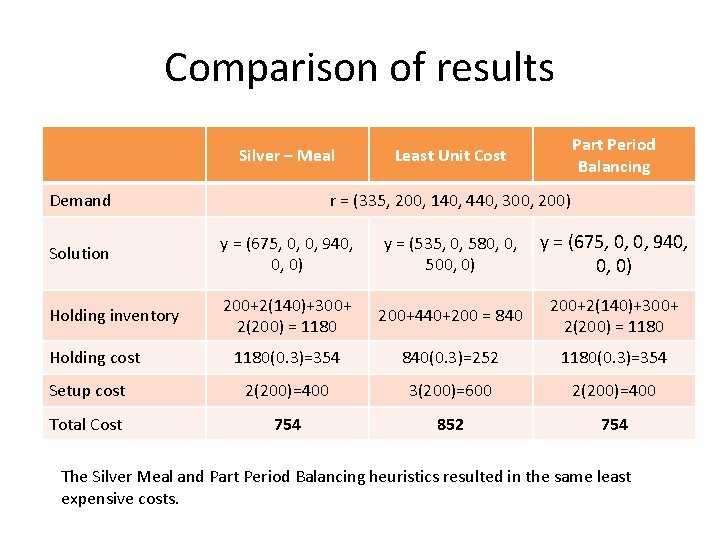
Comparison of Results Silver – Meal Demand Solution Least Unit Cost Part Period Balancing r = (18, 30, 42, 5, 20) y = (48, 0, 47, 0, 20) y = (48, 0, 42, 25, 0) y = (48, 0, 67, 0, 0) Holding inventory 30+5=35 30+20=50 30+5+(2)(20)=75 Holding cost 35(2)=70 50(2)=100 75(2)=150 Setup cost 3(80)=240 2(80)=160 Total Cost 310 340 310 The Silver Meal and Part Period Balancing heuristics resulted in the same least expensive costs.

Exercise 14 – pg 381 • A single inventory item is ordered from an outside supplier. The anticipated demand for this item over the next 12 months is 6, 12, 4, 8, 15, 20, 5, 10, 20, 5, 12. Current inventory of this item is 4, and ending inventory should be 8. Assume a holding cost of $1 period and a setup cost of $40. Determine the order policy for this item based on a) b) c) d) Silver-Meal Least unit cost Part period balancing Which lot-sizing method resulted in the lowest cost for the 12 periods?

Exercise 14 - pg 381 Demand = (6, 12, 4, 8, 15, 20, 5, 10, 20, 5, 12) Starting inventory = 4 Ending inventory = 8 h = 1 K = 40 Net out starting and ending inventories to obtain r = (2, 12, 4, 8, 15, 20, 5, 10, 20, 5, 20) a) Silver Meal Start in period 1: C(1) = 40 C(2) = (40 + 12)/2 = 26 C(3) = [40 + 12 + (2)(4)]/3 = 20 C(4) = [40 + 12 + (2)(4) + (3)(8)]/4 = 21 stop. y 1 = r 1 + r 2 + r 3 = 2 + 12 + 4 = 18

Start in period 4: C(1) = 40 C(2) = (40 + 15)/2 = 27. 5 C(3) = [40 + 15 + (2)(25)]/3 = 35 y 4 = r 4 + r 5 = 8+15 = 23 Stop. Start in period 6: C(1) = 40 C(2) = (40 + 20)/2 = 30 C(3) = [40 + 20 + (2)(5)]/3 = 23. 3333 C(4) = [40 + 20 + (2)(5) + (3)(10)]/4 = 25 Stop. y 6 = r 6 + r 7 + r 8 = 25+20+5 = 50 Start in period 9: C(1) = 40 C(2) = (40 + 20)/2 = 30 C(3) = [40 + 20 + (2)(5)]/3 = 23. 3333 C(4) = [40 + 20 + (2)(5) + (3)(20)]/4 = 32. 5 y 9 = r 9 + r 10 + r 11 = 10+20+5=35 y 12 = r 12 = 20 y= (18, 0, 0, 23, 0, 50, 0, 0, 35, 0, 0, 20)

b) Least unit cost Start in period 1: C(1) = 40/2 = 20 C(2) = (40 + 12)/(2 + 12) = 3. 71 C(3) = (40 + 12 + 8) /(2 + 12 + 4) = 3. 33 C(4) = (40 + 12 + 8 + 24) /(2 + 12 + 4 + 8) = 3. 23 C(5) = (40 + 12 + 8 + 24 + 60) /(2 + 12 + 4 + 8 + 15) = 3. 51 y 1 = r 1 + r 2 + r 3 + r 4 = 2 + 12 + 4 + 8= 26 Start in period 5: C(1) = 40/15 = 2. 67 C(2) = (40 + 25)/(15 + 25) = 1. 625 C(3) = (40 + 25 + 40)/(15 + 20) = 1. 75 y 5 = r 5 + r 6 = 15+25 = 40 Start in period 7: C(1) = 40/20 = 2 C(2) = (40 + 5)/(20 + 5) = 1. 8 C(3) = (40 + 5 + 20)/(20 + 5 + 10) = 1. 86 y 7 = r 7 + r 8 = 20+5= 25 Stop.

Start in period 9: C(1) = 40/10 = 4 C(2) = (40 + 20)/(10 + 20) = 2 C(3) = (40 + 20 + 10)/(10 + 20 + 5) = 2 C(4) = (40 + 20 + 10 + 60)/(10 + 20 + 5 + 20) = 2. 3636 y 9 = r 9 + r 10 + r 11 = 10+20+5=35 y 12 = r 12 = 20 y= (26, 0, 0, 0, 40, 0, 25, 0, 35, 0, 0, 20)

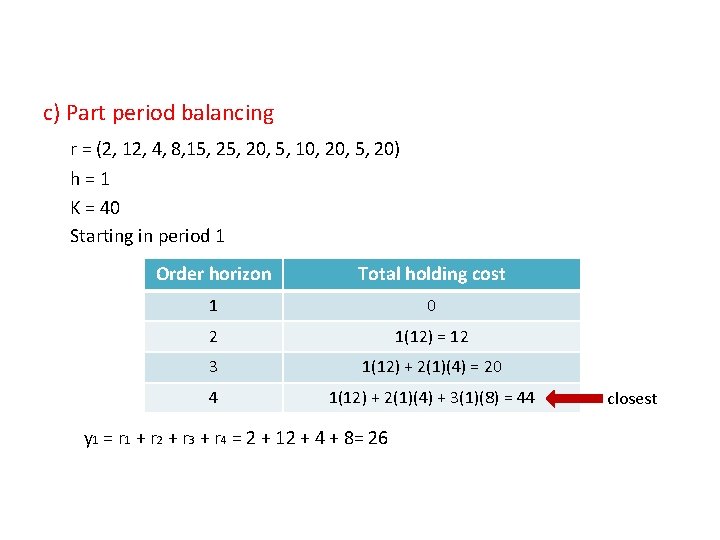
c) Part period balancing r = (2, 12, 4, 8, 15, 20, 5, 10, 20, 5, 20) h = 1 K = 40 Starting in period 1 Order horizon Total holding cost 1 0 2 1(12) = 12 3 1(12) + 2(1)(4) = 20 4 1(12) + 2(1)(4) + 3(1)(8) = 44 y 1 = r 1 + r 2 + r 3 + r 4 = 2 + 12 + 4 + 8= 26 closest

• We start again in period 5 Order horizon Total holding cost 1 0 2 1(25) = 25 3 1(25) + 2(1)(20) = 65 closest y 5 = r 5 + r 6 = 15+25 = 40 • Start in period 7 Order horizon Total holding cost 1 0 2 1(5) = 5 3 1(5) + 2(1)(10) = 25 4 1(5) + 2(1)(10) + 3(1)(20) = 85 y 7 = r 7 + r 8 + r 9= 20+5+10= 35 closest

• Start in period 10 Order horizon Total holding cost 1 0 2 1(5) = 5 3 1(5) + 2(1)(20) = 45 y 10 = r 10 + r 11 + r 12 = 20+5+20 = 45 y = (26, 0, 0, 0, 40, 0, 35, 0, 0, 45, 0, 0) closest

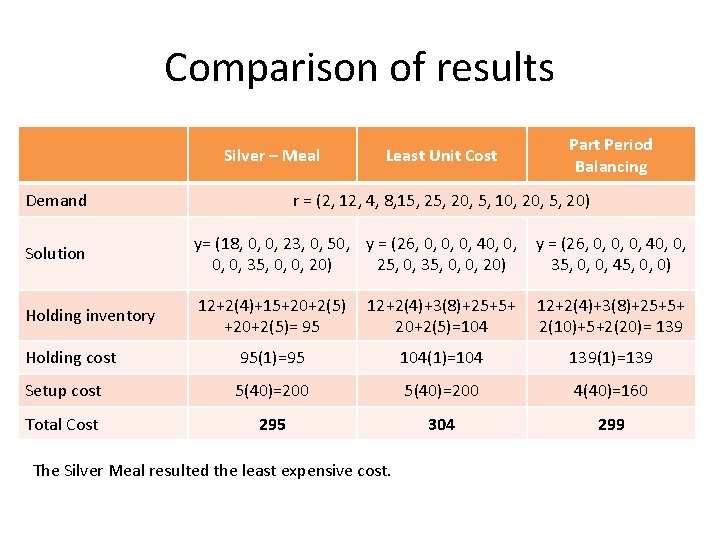
Comparison of results Silver – Meal Least Unit Cost Part Period Balancing Demand r = (2, 12, 4, 8, 15, 20, 5, 10, 20, 5, 20) Solution y= (18, 0, 0, 23, 0, 50, y = (26, 0, 0, 0, 40, 0, 35, 0, 0, 20) 25, 0, 35, 0, 0, 20) 35, 0, 0, 45, 0, 0) Holding inventory 12+2(4)+15+20+2(5)= 95 12+2(4)+3(8)+25+5+ 20+2(5)=104 12+2(4)+3(8)+25+5+ 2(10)+5+2(20)= 139 Holding cost 95(1)=95 104(1)=104 139(1)=139 Setup cost 5(40)=200 4(40)=160 304 299 Total Cost 295 The Silver Meal resulted the least expensive cost.

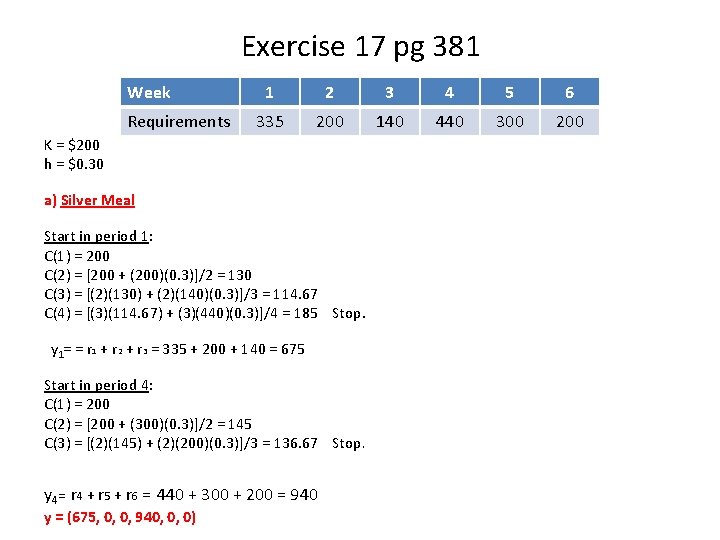
Exercise 17 – pg 381 • The time-phased net requirements for the base assembly in a table lamp over the next six weeks are Week Requirements 1 2 3 4 5 6 335 200 140 440 300 200 • The setup cost for the construction of the base assembly is $200, and the holding cost is $0. 30 per assembly per week a) b) c) d) Determine the lot sizes using the Silver-Meal heuristic Determine the lot sizes using the least unit cost heuristic Determine the lot sizes using part period balancing Which lot-sizing method resulted in the lowest cost for the 6 periods?

Exercise 17 pg 381 Week Requirements 1 2 3 4 5 6 335 200 140 440 300 200 K = $200 h = $0. 30 a) Silver Meal Start in period 1: C(1) = 200 C(2) = [200 + (200)(0. 3)]/2 = 130 C(3) = [(2)(130) + (2)(140)(0. 3)]/3 = 114. 67 C(4) = [(3)(114. 67) + (3)(440)(0. 3)]/4 = 185 Stop. y 1= = r 1 + r 2 + r 3 = 335 + 200 + 140 = 675 Start in period 4: C(1) = 200 C(2) = [200 + (300)(0. 3)]/2 = 145 C(3) = [(2)(145) + (2)(200)(0. 3)]/3 = 136. 67 Stop. y 4= r 4 + r 5 + r 6 = 440 + 300 + 200 = 940 y = (675, 0, 0, 940, 0, 0)

b) Least unit cost Start in period 1: C(1) = 200/335 = 0. 597 C(2) = [200 + (200)(0. 3)]/(335 + 200) = 0. 486 C(3) = [200 + (200)(0. 3) + (140)(2)(0. 3)]/(335 + 200 + 140) = 0. 51 Stop. y 1= r 1 + r 2 = 335 + 200 = 535 Start in period 3: C(1) = 200/140 = 1. 428 C(2) = [200 + (440)(0. 3)]/(140 + 440) = 0. 572 C(3) = [200 + (440)(0. 3) + (300)(2)(0. 3)]/(140 + 440 + 300) = 0. 58 y 3= r 3 + r 4 = 140 + 440 = 580 Start in period 5: C(1) = 200/300 = 0. 67 C(2) = [200 + (200)(0. 3)]/(300 + 200) = 0. 52 y 5 = r 5 + r 6 = 300 + 200 = 500 y = (535, 0, 580, 0, 500, 0) Stop.

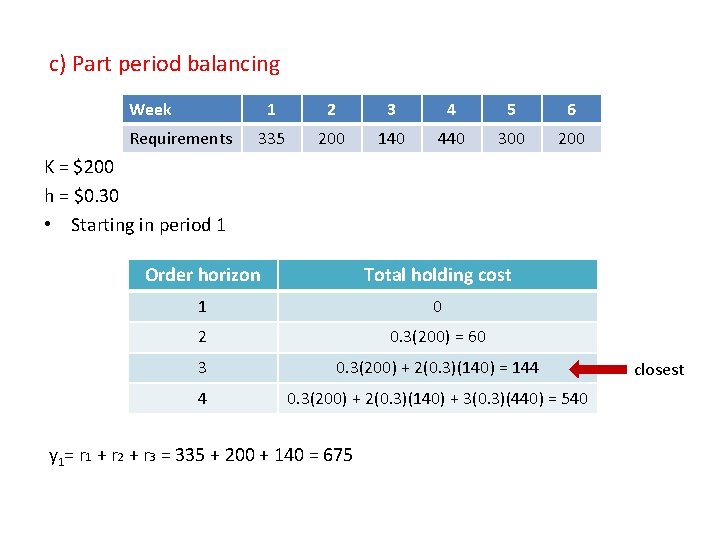
c) Part period balancing Week Requirements 1 2 3 4 5 6 335 200 140 440 300 200 K = $200 h = $0. 30 • Starting in period 1 Order horizon Total holding cost 1 0 2 0. 3(200) = 60 3 0. 3(200) + 2(0. 3)(140) = 144 4 0. 3(200) + 2(0. 3)(140) + 3(0. 3)(440) = 540 y 1= r 1 + r 2 + r 3 = 335 + 200 + 140 = 675 closest

• Starting in period 4 Order horizon Total holding cost 1 0 2 0. 3(300) = 90 3 0. 3(300) + 2(0. 3)(200) = 210 y 4= r 4 + r 5 + r 6 = 440 + 300 + 200 = 940 y = (675, 0, 0, 940, 0, 0) closest

Comparison of results Silver – Meal Demand Part Period Balancing Least Unit Cost r = (335, 200, 140, 440, 300, 200) Solution y = (675, 0, 0, 940, 0, 0) y = (535, 0, 580, 0, 500, 0) y = (675, 0, 0, 940, 0, 0) Holding inventory 200+2(140)+300+ 2(200) = 1180 200+440+200 = 840 200+2(140)+300+ 2(200) = 1180(0. 3)=354 840(0. 3)=252 1180(0. 3)=354 Setup cost 2(200)=400 3(200)=600 2(200)=400 Total Cost 754 852 754 Holding cost The Silver Meal and Part Period Balancing heuristics resulted in the same least expensive costs.