AlternatingCurrent Circuits Means of power for many appliances

Alternating-Current Circuits • Means of power for many appliances we rely on to work in our homes, schools, offices, etc. • Circuits put together all components we have previously seen including resistors, inductors, and capacitors and are driven by a sinusoidal voltage. • What can we get from these circuits? • The amplitude and time characteristics of the alternating current • Discussion concluded with transformers, power transmission, and electrical filters

AC Sources: • Elements of AC circuit elements along with the power source provide and alternating voltage (Δν) described by: Δν=Δvmaxsinωt • Sources include: electric outlets and generators • Due to the sinusoidal properties of the voltage with time, the voltage is positive during half of the cycle and negative during the other half

AC Sources: • The angular frequency for the AC voltage is: ω = 2πƒ = 2π/T ƒ = frequency T = period • The source determines the frequency of the current connected to it

Resistors in an AC Circuit: • Considering a circuit with a resistor: • At any instant, the algebraic sum of the voltages around a closed loop in a circuit must be zero by Kirchhoff’s loop rule, so the voltage across the resistor is: Δν – i. RR = 0 • To find the instantaneous current in the resistor substitute Δvmaxsinωt for Δν: i. R = Δν/R = (Δvmax/R) sinωt = Imaxsinωt • Imax is the maximum current: Imax=ΔVmax/R • The instantaneous voltage across a resistor is: ΔνR=i. RR=Imax. Rsinωt

Resistors in an AC Circuit: • The average current in an AC circuit is important to determine • We call this average current the rms current and relate it to the I max by: Irms = Imax/√ 2 also related to voltage by: ΔVrms = Δvmax/√ 2 • The average power delivered to a resistor that carries and alternating current is: Pavg = I 2 rms. R • The voltage we receive to power our appliances from a wall outlet is 120 V. Because this source is an AC current, the 120 V is described as an rms value.

Inductors in an AC Circuit: • Considering a circuit with and inductor: • Kirchhoff’s rule for and inductor in a loop circuit gives: Δν – L(di. L/dt) = 0 • To find the instantaneous current in the inductor substitute Δvmaxsinωt for Δν: Δν = L(di. L/dt) = Δvmaxsinωt • Solving for di. L gives: di. L =( ΔVmax/L)sinωt dt • Integrating this expression give the instantaneous current i. L in the inductor as a function of time: i. L = (Δvmax/L) sinωt dt = -(ΔVmax/ωL) cos ωt

Inductors in an AC Circuit: • The previous equation can be expressed differently by substituting cos ωt = -sin (ωt – π/2): i. L = (Δvmax/ωL) sin (ωt – π/2) • The instantaneous current in the inductor and the instantaneous voltage across the inductor are out of phase by π/2 radians. The plot shows:

Inductors in an AC Circuit: • The current in an inductive circuit reaches its maximum value when cosωt=± 1: Imax=Δvmax/ωL • ωL behaves the same as resistance in a current so it is given the same units as resistance (Ω) • We define ωL as inductive reactance (XL): XL=ωL • Therefore we can write: Imax=Δvmax/XL • The rms value for an inductor is found by: Irms=Δvrms/XL • The instantaneous voltage across and inductor is: ΔνL = -L(di. L/dt) = -Δvmaxsinωt = -Imax. XLsinωt

Capacitors in an AC Circuit: • Considering a circuit with and capacitor: • Kirchhoff’s rule for and capacitor in a loop circuit gives: Δν – (q/C) = 0 • To find the instantaneous current in the capacitor substitute Δvmaxsinωt for Δν: q = CΔVmaxsinωt • The instantaneous current in the circuit is: i. C = dq/dt = ωCΔVmaxcosωt • Using cosωt = sin (ωt + π/2), we get: i. C = ωCΔVmaxsin(ωt + π/2) • The current is also π/2 radians out of phase with the voltage across a capacitor

Inductors in an AC Circuit: • The current in an capacitive circuit reaches its maximum value when cosωt=± 1: Imax = ωCΔVmax = ΔVmax/(1/ωC) • 1/ωC behaves the same as resistance in a current so it is given the same units as resistance (Ω) • We define 1/ωC as capacitive reactance (Xc): Xc=1/ωC • Therefore we can write: Imax=Δvmax/XC • The rms value for an inductor is found by: Irms=Δvrms/XC • The instantaneous voltage across and inductor is: ΔνC = Δvmaxsinωt = Imax. XCsinωt • As frequency of the voltage source increases, the capacitive reactance decreases and the maximum current increases

The RLC Series Circuit: • We have considered all the parts separately, but now we will see how the circuit act with the resistor, inductor, and capacitor in a seires

The RLC Series Circuit: • The instantaneous voltages across the three circuit elements are: ΔνR = Imax. Rsinωt = ΔVRsinωt ΔνL = Imax. XLsin(ωt + π/2) = ΔVLcosωt ΔνC = Imax. XCsin(ωt + π/2) = -ΔVCcosωt • The sum of these three voltages must equal the voltage from the AC source, but they cannot be added directly because three voltages have different phase relationships with the current. • We can relate the voltages by: Δvmax = √[ΔVR 2 + (ΔVL – ΔVC)2 = √[(Imax. R)2 + (Imax. XL – Imax. XC)2] Δvmax = Imax √(R 2 + (XL – XC)2] • We can then express the maximum current as: Imax= Δvmax/√(R 2 + (XL – XC)2]

The RLC Series Circuit: • The denominator of the fraction Imax= Δvmax/√(R 2 + (XL – XC)2] plays a role in resistance and is called impedance (Z) of a circuit: Z = √(R 2 + (XL – XC)2 • Impedance also has the units of ohms just as resistance. We can rewirte the equation for maximum current to be: Imax = Δvmax/Z • The phase angle Φ between the current and the voltage is found as: Φ = tan-1[(ΔVL-ΔVC)/ΔVR] = tan-1[(Imax. XL – Imax. XC)/Iman. R] So, Φ = tan-1[(XL-XC)/R]

Power in an AC Circuit: • The instantaneous power delivered by an AC source to a circuit is the product of the current and the applied voltage. • For the RLC circuit, we can express the instantaneous power (P) as: P = iΔν = Imaxsin(ωt – Φ) Δvmaxsinωt P = Imax Δvmaxsinωt sin(ωt-Φ) • This expression leads to a complicated function of time so we will look at power as an average over one or more cycles. Therefore we will use: P = Imax Δvmax sin 2 ωt cos Φ – Imax Δvmax sinωt cosωt sinΦ • Removing the constants, we can simplify this expression to express average power as: Pavg = ½Imax Δvmax cosΦ • Expressing average power in terms of the rms current and rms voltage gives: Pavg = Irms ΔVrms cosΦ or Pavg = I 2 rms. R or Pavg = Irms ΔVrms

Resonance in a Series RLC circuit: • An RLC circuit is an electrical oscillating system. • The rms current is written: • Substituting for Z we get: Irms = ΔVrms/Z Z = impedance Irms = Δvrms/√(R 2 + (XL – XC)2] • Because the impedance depends on the frequency of the source, the current in the RLC circuit also depends on the frequency. The angular frequency (ω0) at which XLXC=0 is called the resonance frequency of the circuit. • To find ω0, we set XL=XC, which gives: ω0 = 1/√(LC)

The Transformer and Power Transmission: • The power traveling through power lines is delivered at a high voltage around 20, 000 V. There must be a way to decrease the voltage to the 120 V that is delivered by our power outlets. • AC Transformers consists of two coils of wire would around a core of iron are responsible for this decrease in voltage from the power delivery station to our homes.

The Transformer and Power Transmission: • The coil on the left is considered the primary coil because it is connected to the input alternating-voltage source and has N 1 turns. The coil on the right consisting of N 2 turns is called the secondary winding. • The iron core increases the magnetic flux through the coil to provide a medium in which nearly all the magnetic field lines through one coil pass through the other coil.

The Transformer and Power Transmission: • Using transformers, Faraday’s law states that the voltage Δν 1 = -N 1 (dΦB/dt) where, ΦB is the magnetic flux through each turn • If we assume all magnetic field lines remain within the iron core, the flux through each turn of the primary equals the flux through each turn of the secondary. Therefore the voltage across the secondary is: Δν 2 = -N 2 (dΦB/dt) • Solving for dΦB/dt and substituting the result into Δν 2 = -N 2 (dΦB/dt) we get: Δν 2 = (N 2/N 1) Δν 1

Filters: • Filters can be designed to respond to different frequencies • The input voltage is across the series combination of the two elements. • The output is the voltage across the resistor • At low frequencies, Δvout is much smaller than Δvin, whereas at high frequencies, the two voltages are equal • Because the circuit preferentially passes signals of higher frequency while blocking low –frequency signals, the circuit is called an RC high-pass filter • The capacitor blocks out direct current and AC current at low frequencies

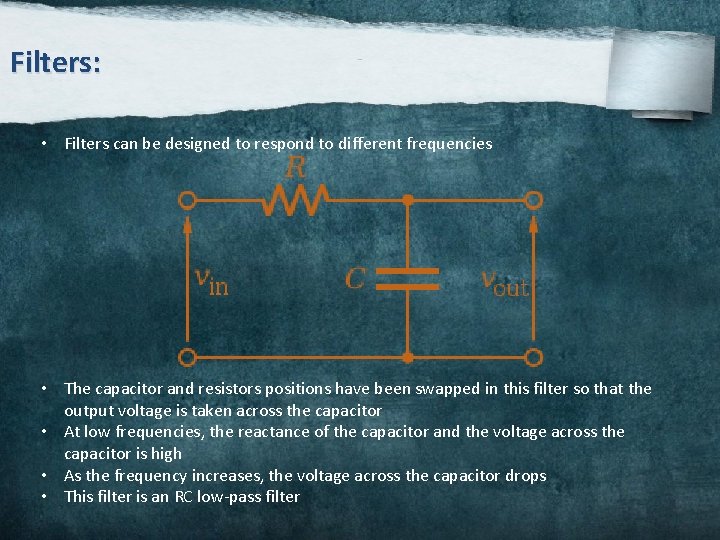
Filters: • Filters can be designed to respond to different frequencies • The capacitor and resistors positions have been swapped in this filter so that the output voltage is taken across the capacitor • At low frequencies, the reactance of the capacitor and the voltage across the capacitor is high • As the frequency increases, the voltage across the capacitor drops • This filter is an RC low-pass filter