ALTERNATING VOLTAGES AND CURRENT Chapter 1 Alternating Current

ALTERNATING VOLTAGES AND CURRENT Chapter 1 - Alternating Current

DIRECT CURRENT (DC) – IS WHEN THE CURRENT FLOWS IN ONLY ONE DIRECTION. Constant flow of electric charge EX: BATTERY ALTERNATING CURRENT AC) – THE CURRENT FLOWS IN ONE DIRECTION THE OTHER. Electrical current whose magnitude and direction vary cyclically, as opposed to direct current whose direction remains constant. EX: OUTLETS Chapter 1 - Alternating Current

By rotating a magnetic field within a stationary coil By rotating a coil in a magnetic field Chapter 1 - Alternating Current

A voltage supplied by a battery or other DC source has a certain polarity and remains constant. Alternating Current (AC) varies in polarity and amplitude. AC is an important part of electrical and electronic systems. Chapter 1 - Alternating Current 4

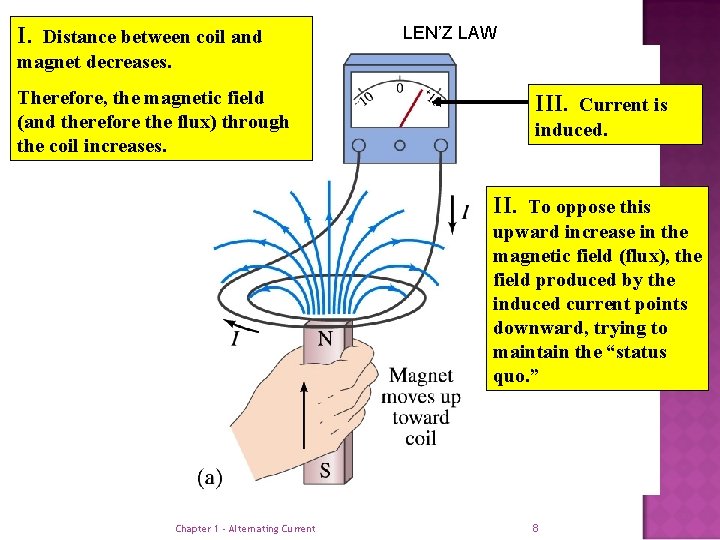
Faraday’s Laws of electromagnetic Induction. Induced electromotive field Any change in the magnetic environment of a coil of wire will cause a voltage (emf) to be "induced" in the coil. e. m. f, e = -N d dt N = Number of turn = Magnetic Flux Lenz’s law An electromagnetic field interacting with a conductor will generate electrical current that induces a counter magnetic field that opposes the magnetic field generating the current. Chapter 1 - Alternating Current

29 -1 INDUCED EMF Faraday found that a changing magnetic field produces a current. Such a current is called an induced current. Therefore, a changing magnetic field induces an emf. Chapter 1 - Alternating Current 6

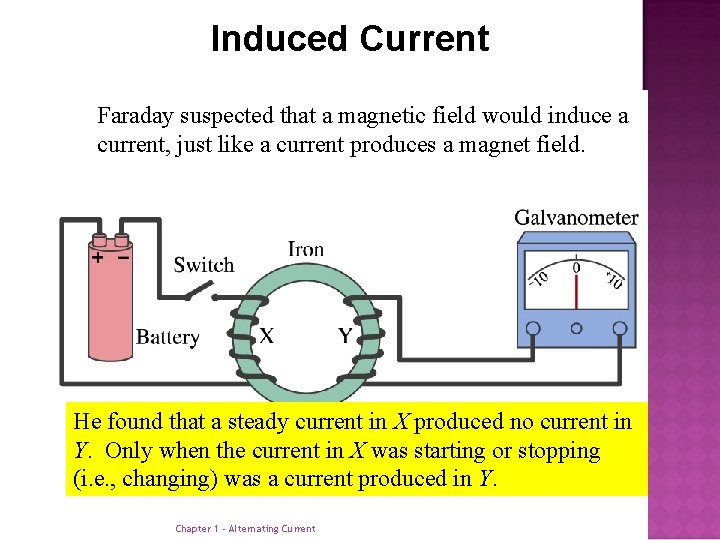
Induced Current Faraday suspected that a magnetic field would induce a current, just like a current produces a magnet field. He found that a steady current in X produced no current in Y. Only when the current in X was starting or stopping (i. e. , changing) was a current produced in Y. Chapter 1 - Alternating Current 7

I. Distance between coil and LEN’Z LAW magnet decreases. Therefore, the magnetic field (and therefore the flux) through the coil increases. III. Current is induced. II. To oppose this upward increase in the magnetic field (flux), the field produced by the induced current points downward, trying to maintain the “status quo. ” Chapter 1 - Alternating Current 8

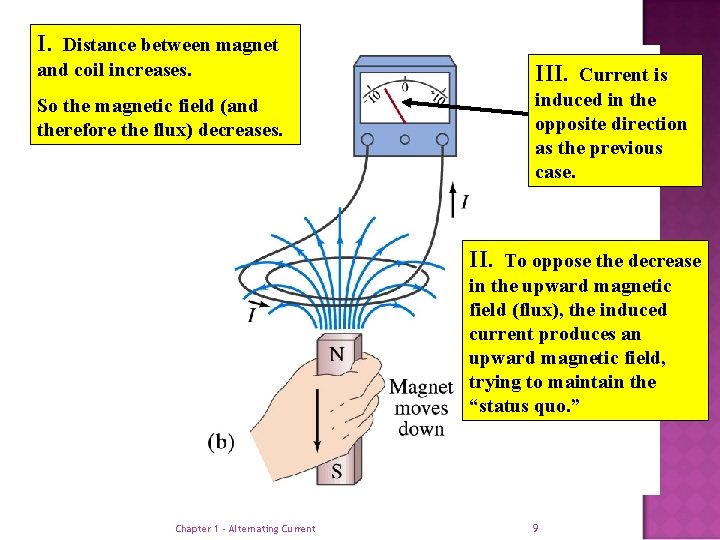
I. Distance between magnet and coil increases. III. Current is So the magnetic field (and therefore the flux) decreases. induced in the opposite direction as the previous case. II. To oppose the decrease in the upward magnetic field (flux), the induced current produces an upward magnetic field, trying to maintain the “status quo. ” Chapter 1 - Alternating Current 9

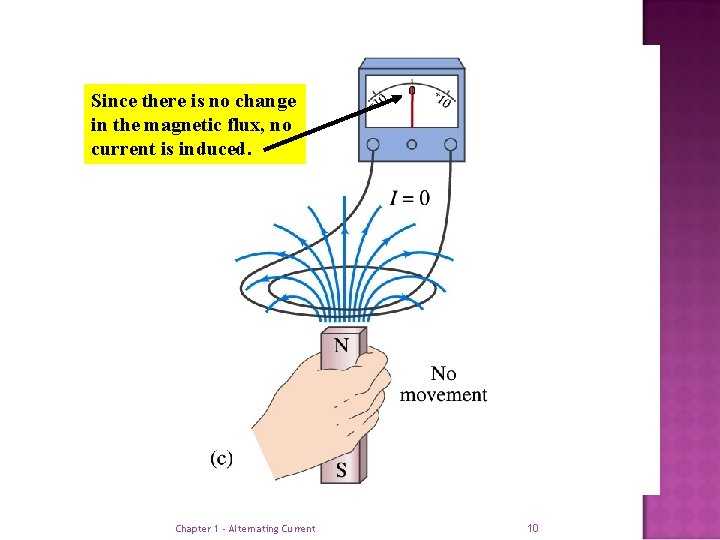
Since there is no change in the magnetic flux, no current is induced. Chapter 1 - Alternating Current 10

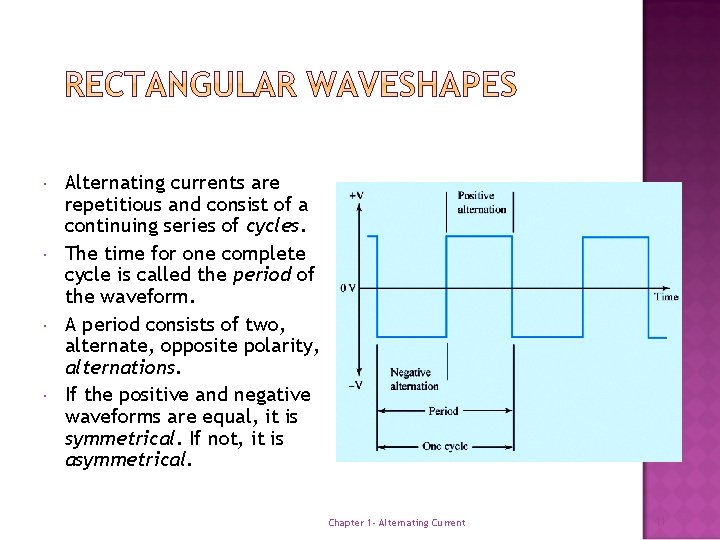
Alternating currents are repetitious and consist of a continuing series of cycles. The time for one complete cycle is called the period of the waveform. A period consists of two, alternate, opposite polarity, alternations. If the positive and negative waveforms are equal, it is symmetrical. If not, it is asymmetrical. Chapter 1 - Alternating Current 11

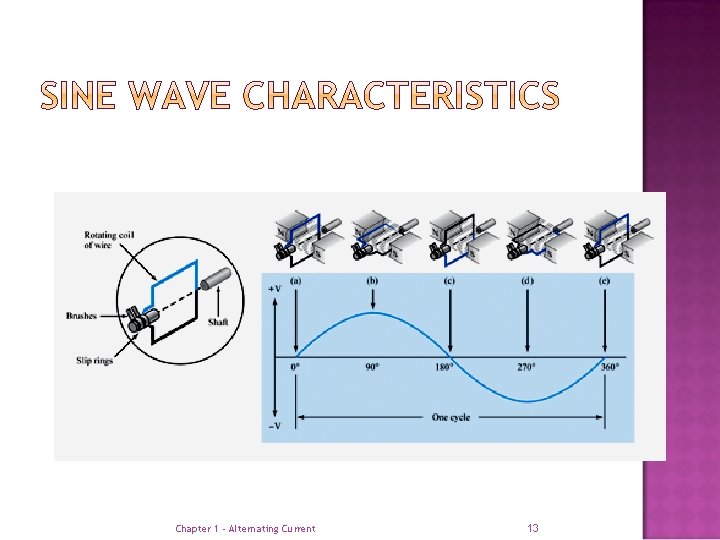
The basis of an AC alternator is a loop of wire rotated in a magnetic field. Slip rings and brushes make continuous electrical connections to the rotating conductor. The magnitude and polarity of the generated voltage is shown on the following slide. Chapter 1 - Alternating Current 12

Chapter 1 - Alternating Current 13

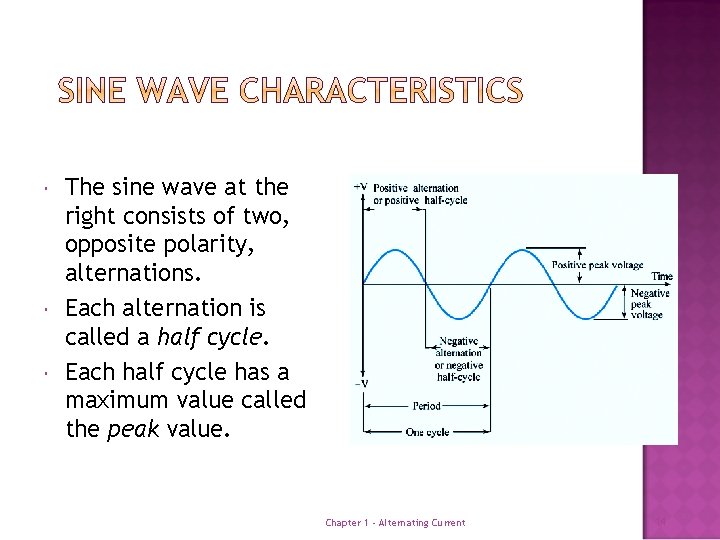
The sine wave at the right consists of two, opposite polarity, alternations. Each alternation is called a half cycle. Each half cycle has a maximum value called the peak value. Chapter 1 - Alternating Current 14

Sine waves may represent voltage, current, or some other parameter. The period of a sine wave is the time from any given point on the cycle to the same point on the following cycle. The period is measured in time (t), and in most cases is measured in seconds or fractions thereof. Chapter 6 - Alternating Current 15

The frequency of a sine wave is the number of complete cycles that occur in one second. Frequency is measured in hertz (Hz). One hertz corresponds to one cycle per second. Frequency and period have an inverse relationship. t = 1/f, and f = 1/t. Frequency-to-period and period-to-frequency conversions are common in electronic calculations. Chapter 6 - Alternating Current 16

• • • The peak value of a sine wave is the maximum voltage (or current) it reaches. Peak voltages occur at two different points in the cycle. One peak is positive, the other is negative. The positive peak occurs at 90º and the negative peak at 270º. The positive and negative have equal amplitudes. Chapter 6 - Alternating Current 17

Another measurement used to describe sine waves are their peak-to-peak values. The peak-to-peak value is the difference between the two peak values. Chapter 6 - Alternating Current 18

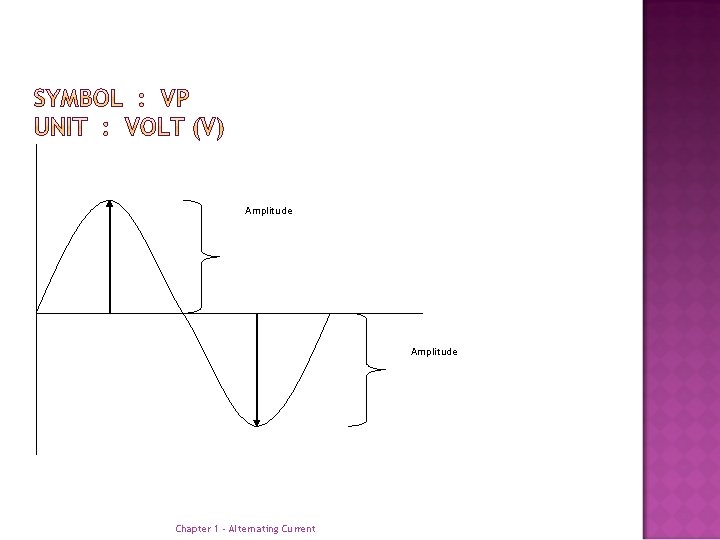
Amplitude Chapter 1 - Alternating Current

The average value of any measured quantity is the sum of all of the intermediate values. The average value of a full sine wave is zero. The average value of one-half cycle of a sine wave is: Vavg = 0. 637 Vp or Iavg = 0. 637 Ip Chapter 6 - Alternating Current 20

• • One of the most important characteristics of a sine wave is its rms or effective value. The rms value describes the sine wave in terms of an equivalent dc voltage. The rms value of a sine wave produces the same heating effect in a resistance as an equal value of dc. The abbreviation rms stands for root-meansquare, and is determined by: Vrms = 0. 707 Vp or Irms = 0. 707 Ip Chapter 6 - Alternating Current 21

Form Factor is defined as the ratio of r. m. s value to the average value. Form factor = = r. m. s value average value 1. 11 Chapter 1 - Alternating Current = 0. 707 peak value 0. 637 peak valur

Crest or Peak or Amplitude Factor Peak factor is defined as the ratio of peak voltage to r. m. s value. Peak Factor = peak value r. m. s value 0. 707 x peak value = 1. 414 Chapter 1 - Alternating Current

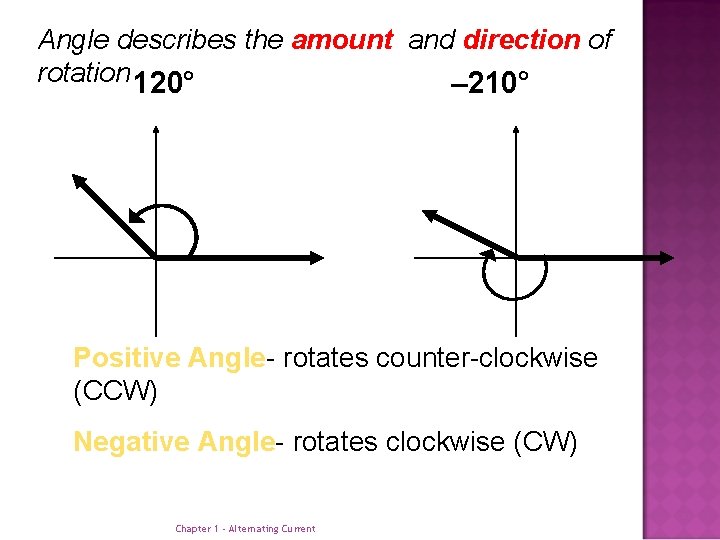
Angle describes the amount and direction of rotation 120° – 210° Positive Angle- rotates counter-clockwise (CCW) Negative Angle- rotates clockwise (CW) Chapter 1 - Alternating Current

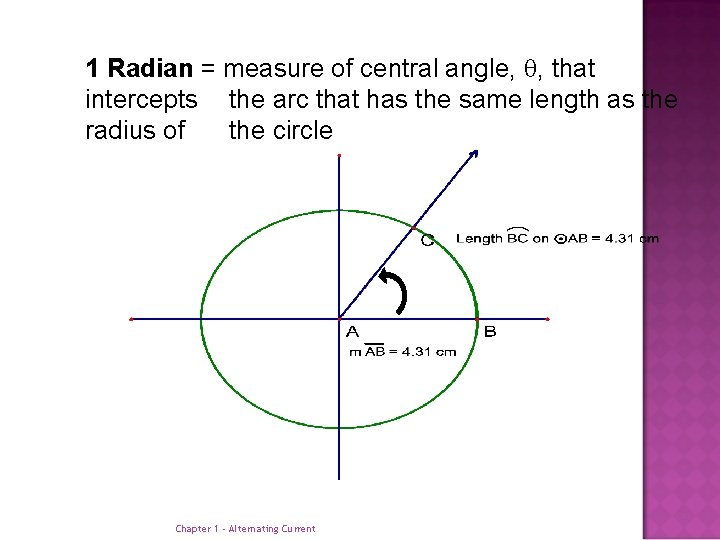
1 Radian = measure of central angle, , that intercepts the arc that has the same length as the radius of the circle Chapter 1 - Alternating Current

Calculate the number of radians in one full circle: C= 0, 2 3. 14 0, 6. 28 0 Chapter 1 - Alternating Current

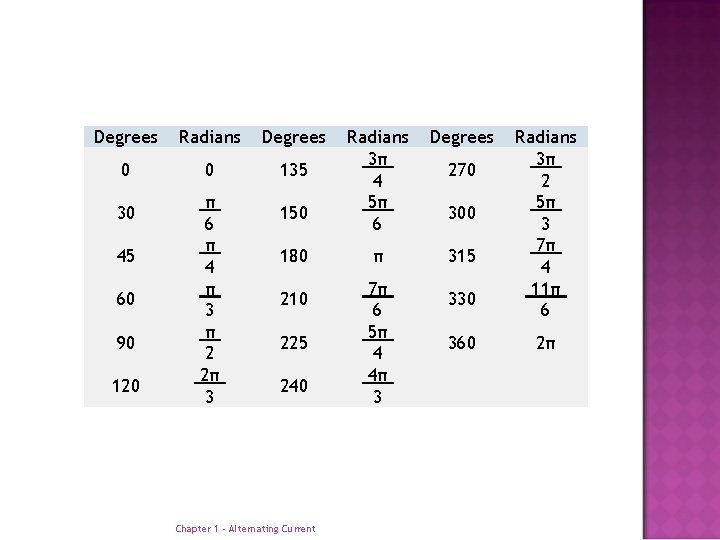
Degrees Radians Degrees 0 0 135 30 45 60 90 120 π 6 π 4 π 3 π 2 2π 3 150 180 210 225 240 Chapter 1 - Alternating Current Radians 3π 4 5π 6 Degrees π 315 7π 6 5π 4 4π 3 270 300 330 360 Radians 3π 2 5π 3 7π 4 11π 6 2π

To convert from degrees radians, multiply by To convert from radians degrees, multiply by Convert to radians: Chapter 1 - Alternating Current

To convert from degrees radians, multiply by To convert from radians degrees, multiply by Convert to degrees: Chapter 1 - Alternating Current So, you think you got it now?

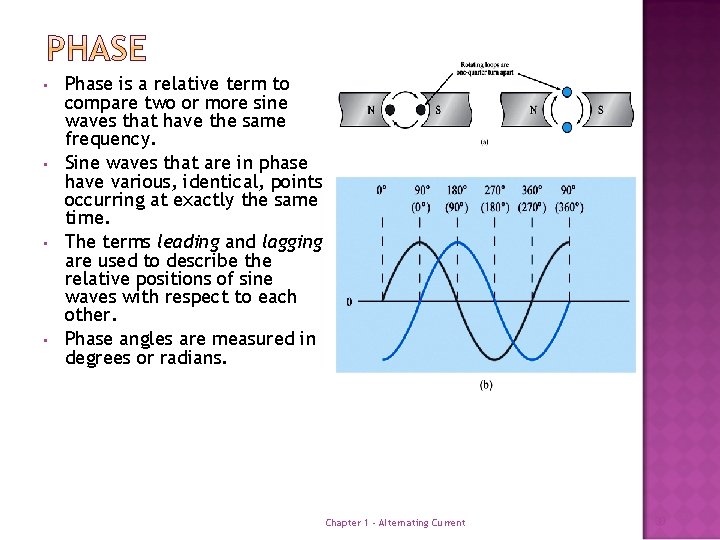
• • Phase is a relative term to compare two or more sine waves that have the same frequency. Sine waves that are in phase have various, identical, points occurring at exactly the same time. The terms leading and lagging are used to describe the relative positions of sine waves with respect to each other. Phase angles are measured in degrees or radians. Chapter 1 - Alternating Current 30

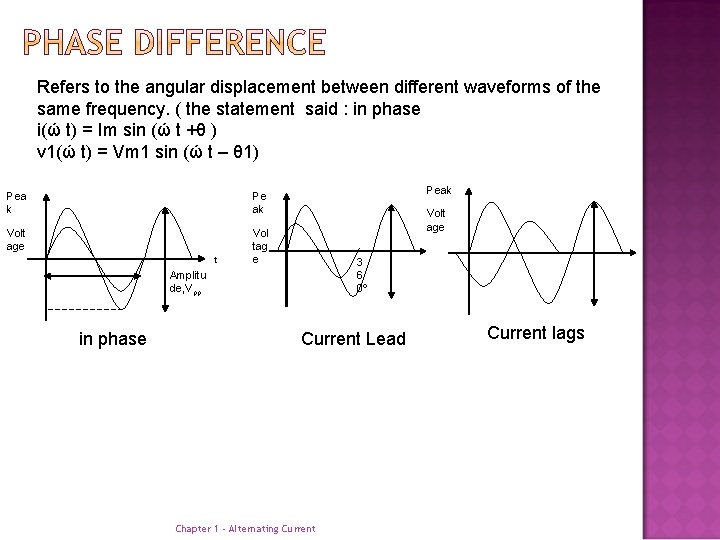
Refers to the angular displacement between different waveforms of the same frequency. ( the statement said : in phase i(ώ t) = Im sin (ώ t +θ ) v 1(ώ t) = Vm 1 sin (ώ t – θ 1) Pea k Pe ak Volt age Vol tag e t Peak Volt age 3 6 0º Amplitu de, Vpp in phase Current Lead Chapter 1 - Alternating Current lags

v(ώt) = Vm sin ώ t i(ώ t) = Im sin (ώ t +θ ) v 1(ώ t) = Vm 1 sin (ώ t – θ 1) 1) i(ώ t) lead v(ώt) with angler θ radian/degree or v(ώt) lag i(ώ t) with angler θ radian/degree 2) v 1(ώ t) lag v(ώt) with angler θ 1 radian or v(ώt) lead v 1(ώ t) with angler θ 1 radian Chapter 1 - Alternating Current

Voltage and current are out of phase by 400, and voltage lags. Using current as the reference, sketch the phasor diagram and the corresponding waveforms. Given v= 20 sin (ώ t + 400 ) and i=18 sin (ώ t - 400 ), draw the phasor diagram, determine phase relationships, and sketch the waveform. Chapter 1 - Alternating Current

We can express the voltage or current at any instant during a sine wave’s cycle. The instantaneous voltage of a sine wave is zero at 0º. Instantaneous voltages (v) and currents (i) are found by: Chapter 6 - Alternating Current 34

• • All signals can be viewed from either of two perspectives: time-domain or frequencydomain. Fourier developed mathematical principles that link together time and frequency domains. A time-domain signal is one whose instantaneous voltage changes over time. Any given waveform can be shown to be composed of one or more sinusoidal signals at specific frequencies and phases (frequency domain) Chapter 6 - Alternating Current 35

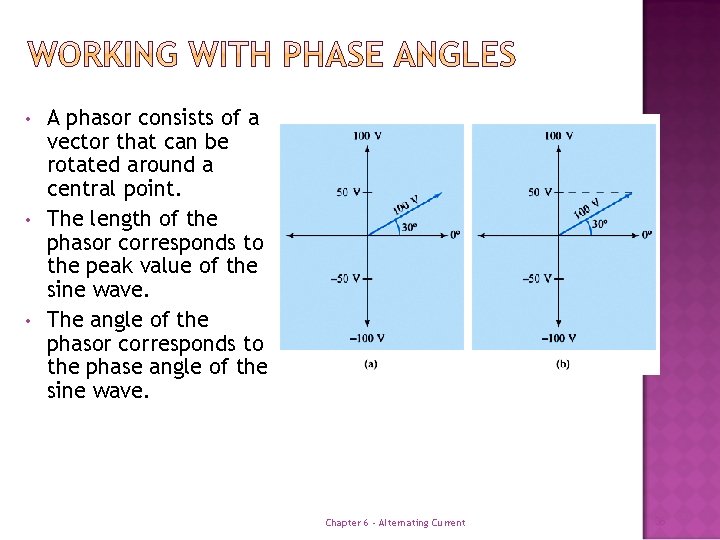
• • • A phasor consists of a vector that can be rotated around a central point. The length of the phasor corresponds to the peak value of the sine wave. The angle of the phasor corresponds to the phase angle of the sine wave. Chapter 6 - Alternating Current 36

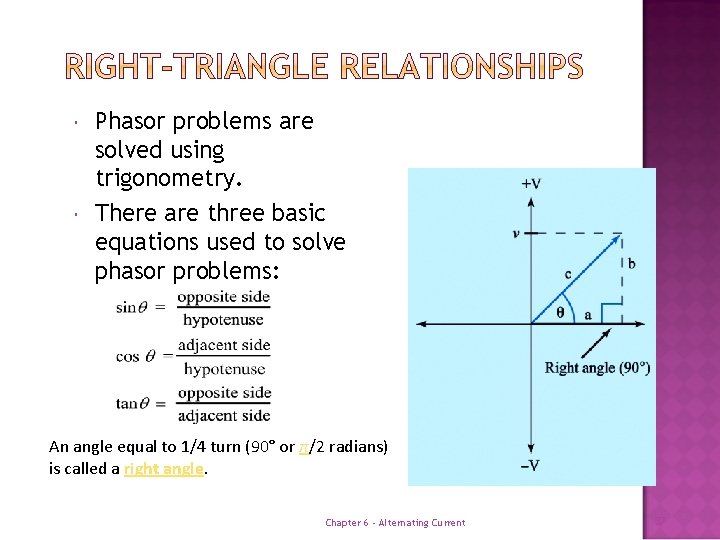
Phasor problems are solved using trigonometry. There are three basic equations used to solve phasor problems: An angle equal to 1/4 turn (90° or π/2 radians) is called a right angle. Chapter 6 - Alternating Current 37

• • • AC circuits composed of resistors can be analyzed using Ohm’s and Kirchoff’s Laws just as with dc circuits. Care must be taken that the correct formulas are used for peak voltages/currents, average voltages/currents, etc. Typically, power ratings are rms values in an ac circuit. Chapter 1 - Alternating Current 38

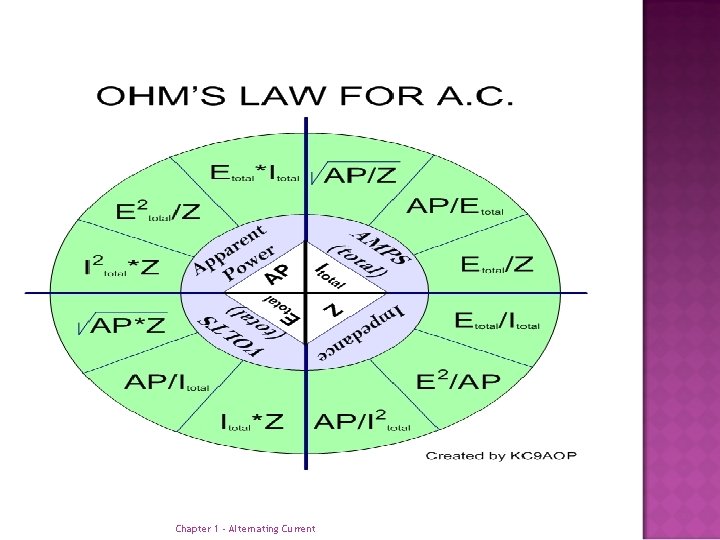
In general, Ohm's law cannot be applied to alternating-current circuits since it does not consider the reactance which is always present in such circuits. However, by a modification of Ohm's law which does take into consideration the effect of reactance we obtain a general law which is applicable to ac circuits. Because the impedance, Z, represents the combined opposition of all the reactances and resistances, this general law for ac is, I=E/Z Chapter 1 - Alternating Current

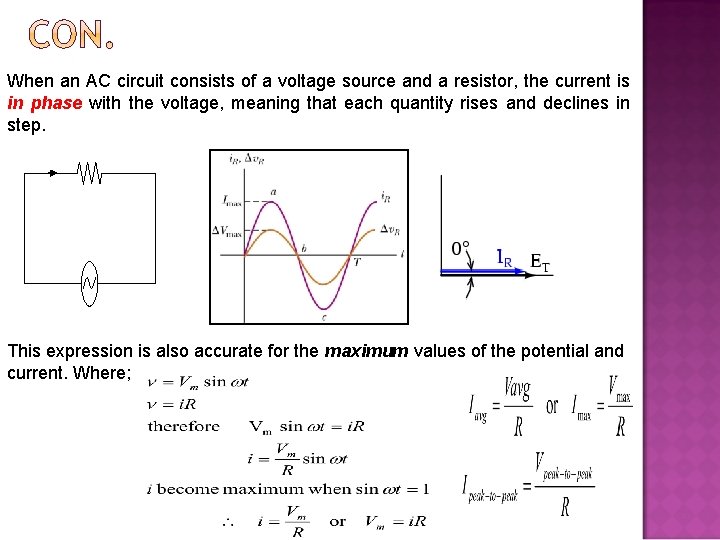
When an AC circuit consists of a voltage source and a resistor, the current is in phase with the voltage, meaning that each quantity rises and declines in step. This expression is also accurate for the maximum values of the potential and current. Where;

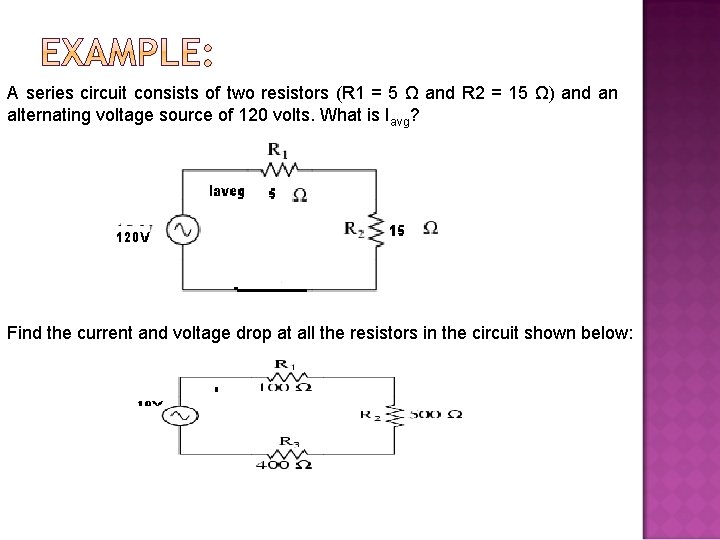
A series circuit consists of two resistors (R 1 = 5 Ω and R 2 = 15 Ω) and an alternating voltage source of 120 volts. What is Iavg? Find the current and voltage drop at all the resistors in the circuit shown below:

KIRCHHOFF’S LAW IN ALTERNATING CURRENT Kirchhoff’s Law can be divided into 2: • Kirchhoff’s Current Law • Kirchhoff’s Voltage Law Kirchhoff’s Current Law At any point in an electrical circuit where change density is not changing in time, the sum of current flowing towards that point is equal to the sum of currents flowing away from that point. Kirchhoff’s Voltage Law The algebraic sum of various potential drops across an electrical circuit is equal to the electromotive force acting on the circuit

Calculate value current that flows to each branch use Kirchhoff’s Law

This power, measured in watts, is the power associated with the total resistance in the circuit To calculate true power, the voltage and current associated with the resistance must be used.

Chapter 1 - Alternating Current

Chapter 1 - Alternating Current

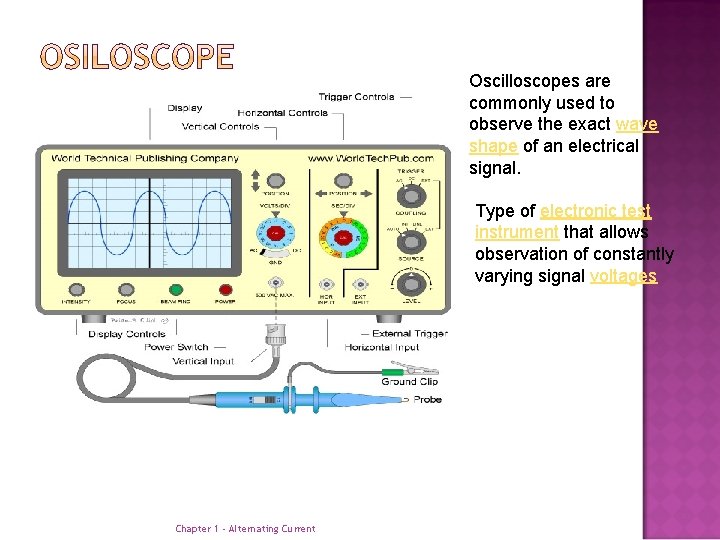
Oscilloscopes are commonly used to observe the exact wave shape of an electrical signal. Type of electronic test instrument that allows observation of constantly varying signal voltages Chapter 1 - Alternating Current

Chapter 1 - Alternating Current

Power To switch the osiclloscope ON or OFF. Focus control This control adjusts CRT focus to obtain the sharpest, most-detailed trace. I Intensity control This adjusts trace brightness. Slow traces on CRT 'scopes need less, and fast ones, especially if they don't repeat very often. Position To position waveform horizontally or vertically Volt/Div To adjust vertical magnification of a waveform Time/Div to adjust horizontal magnification of a waveform Chapter 1 - Alternating Current

Thank You