ALTERNATING VOLTAGE AND CURRENT Example of instantaneous value

ALTERNATING VOLTAGE AND CURRENT

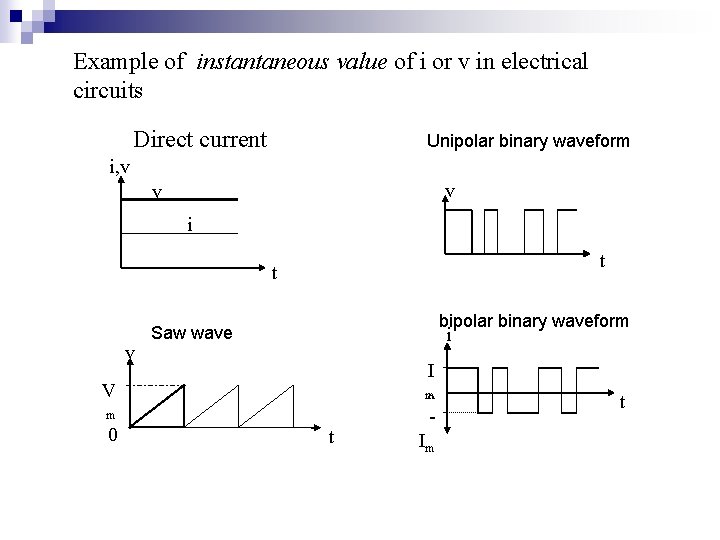
Example of instantaneous value of i or v in electrical circuits Direct current Unipolar binary waveform i, v v v i t t v bipolar binary waveform Saw wave i I V m m 0 t 0 - Im t

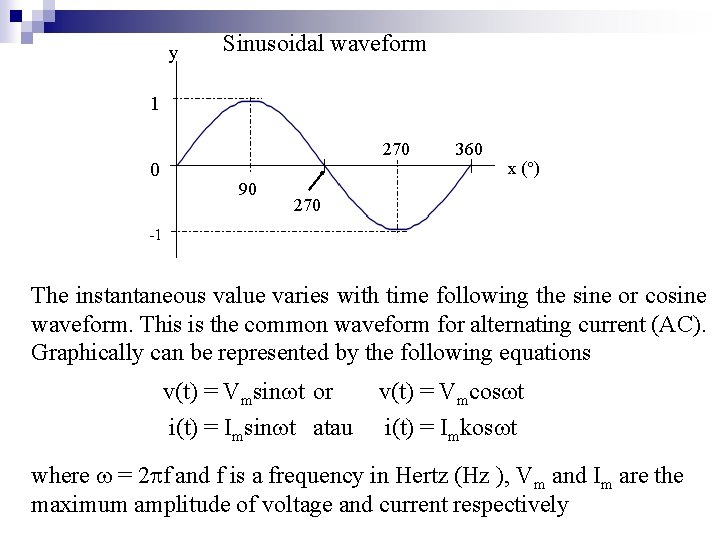
y Sinusoidal waveform 1 0 270 90 360 x ( ) 270 -1 The instantaneous value varies with time following the sine or cosine waveform. This is the common waveform for alternating current (AC). Graphically can be represented by the following equations v(t) = Vmsin t or i(t) = Imsin t atau v(t) = Vmcos t i(t) = Imkos t where = 2 f and f is a frequency in Hertz (Hz ), Vm and Im are the maximum amplitude of voltage and current respectively

Features of the voltage waveform v (V) Vm VP-P 0 -V 3 T/4 T t (s) T/2 m 1. Above figure represents one cylcle of voltage waveform which is methamatically represented by v = Vmsin t. Vm to –Vm is called VP-P (peak to peak value). 2. One cycle is equivalent to one wavelength or 360 o or 2 in degree. 3. One cycle also is said to have a periodic time T (sec). 4. A number of cycle per sec is said to have a frequency f (Hz) 5. The relationship between T and f is or

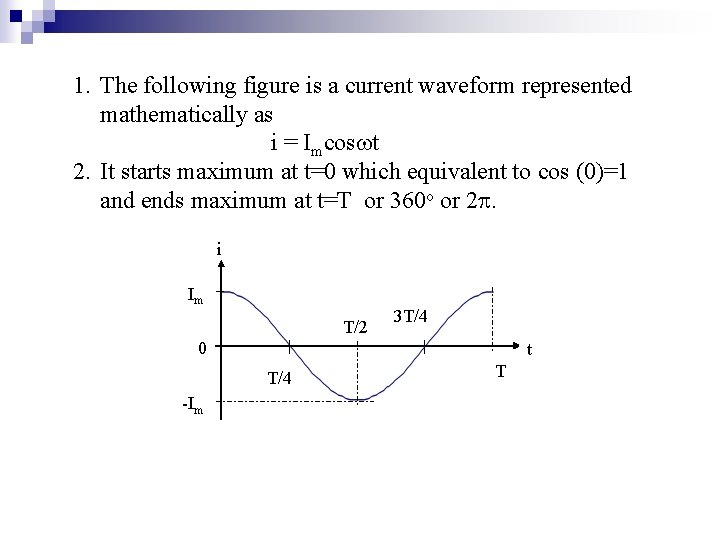
1. The following figure is a current waveform represented mathematically as i = Imcos t 2. It starts maximum at t=0 which equivalent to cos (0)=1 and ends maximum at t=T or 360 o or 2. i Im T/2 3 T/4 0 t T/4 -Im T

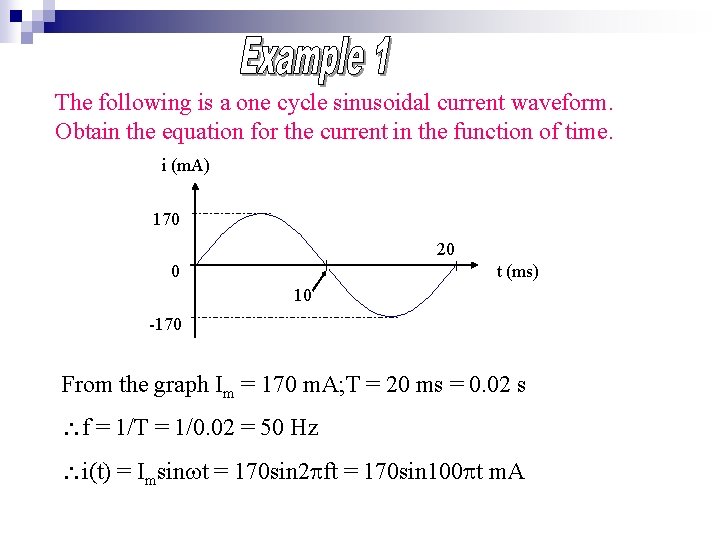
The following is a one cycle sinusoidal current waveform. Obtain the equation for the current in the function of time. i (m. A) 170 20 0 t (ms) 10 -170 From the graph Im = 170 m. A; T = 20 ms = 0. 02 s f = 1/T = 1/0. 02 = 50 Hz i(t) = Imsin t = 170 sin 2 ft = 170 sin 100 t m. A

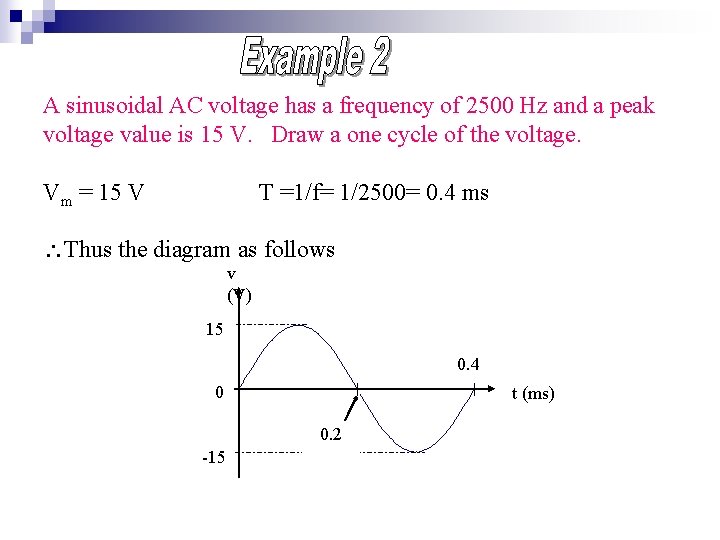
A sinusoidal AC voltage has a frequency of 2500 Hz and a peak voltage value is 15 V. Draw a one cycle of the voltage. Vm = 15 V T =1/f= 1/2500= 0. 4 ms Thus the diagram as follows v (V) 15 0. 4 0 t (ms) 0. 2 -15

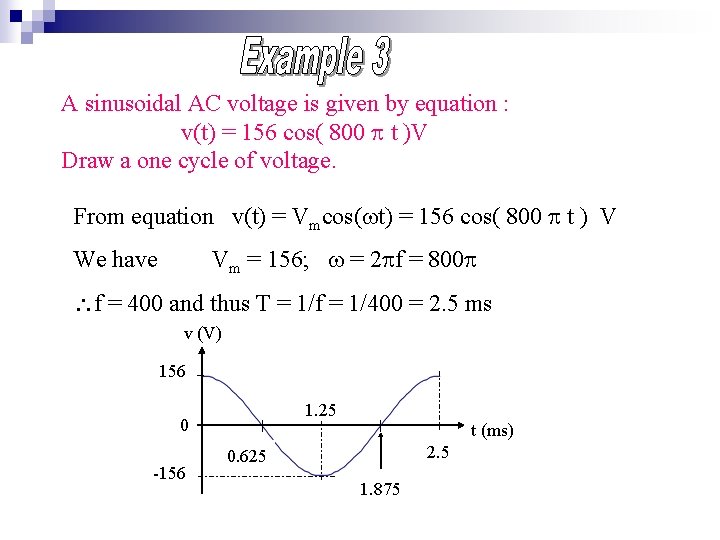
A sinusoidal AC voltage is given by equation : v(t) = 156 cos( 800 t )V Draw a one cycle of voltage. From equation v(t) = Vmcos( t) = 156 cos( 800 t ) V Vm = 156; = 2 f = 800 We have f = 400 and thus T = 1/f = 1/400 = 2. 5 ms v (V) 156 1. 25 0 -156 t (ms) 2. 5 0. 625 1. 875

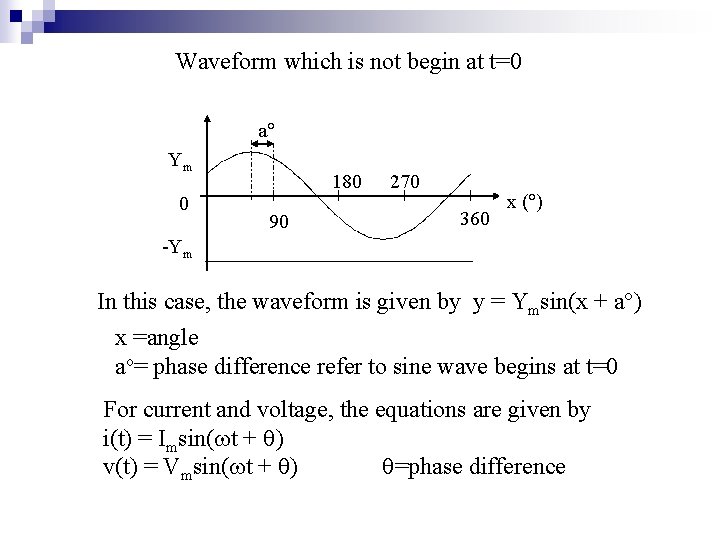
Waveform which is not begin at t=0 a Ym 0 180 90 270 360 x ( ) -Ym In this case, the waveform is given by y = Ymsin(x + a ) x =angle ao= phase difference refer to sine wave begins at t=0 For current and voltage, the equations are given by i(t) = Imsin( t + ) v(t) = Vmsin( t + ) =phase difference

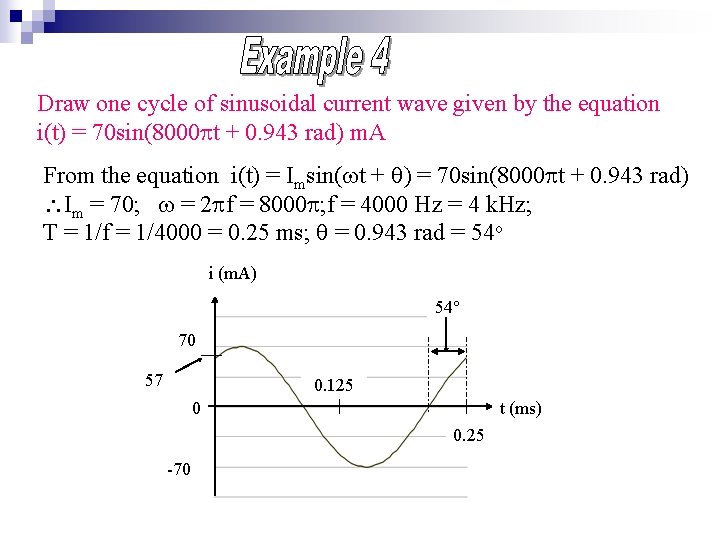
Draw one cycle of sinusoidal current wave given by the equation i(t) = 70 sin(8000 t + 0. 943 rad) m. A From the equation i(t) = Imsin( t + ) = 70 sin(8000 t + 0. 943 rad) Im = 70; = 2 f = 8000 ; f = 4000 Hz = 4 k. Hz; T = 1/f = 1/4000 = 0. 25 ms; = 0. 943 rad = 54 o i (m. A) 54 70 57 0. 125 0 t (ms) 0. 25 -70

Obtain the equation of the following waveform From waveform: T = 20 ms f=1/T = 1/0. 02 = 50 Hz = 2 f = 100 3 ms = 3 x 360/20 = 54 = 90 – 54 = 36 Vm = 339 V Equation for voltage: v(t) = Vmsin( t + ) = 339 sin(100 t + 36 )

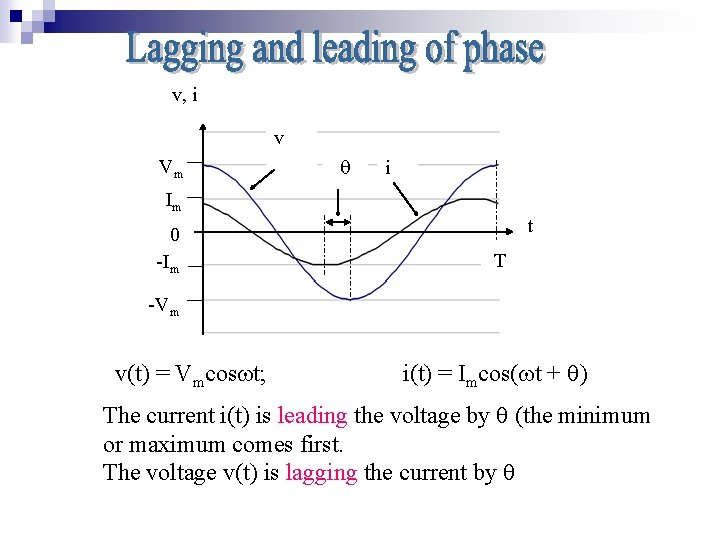
v, i v Vm i Im t 0 -Im T -Vm v(t) = Vmcos t; i(t) = Imcos( t + ) The current i(t) is leading the voltage by (the minimum or maximum comes first. The voltage v(t) is lagging the current by

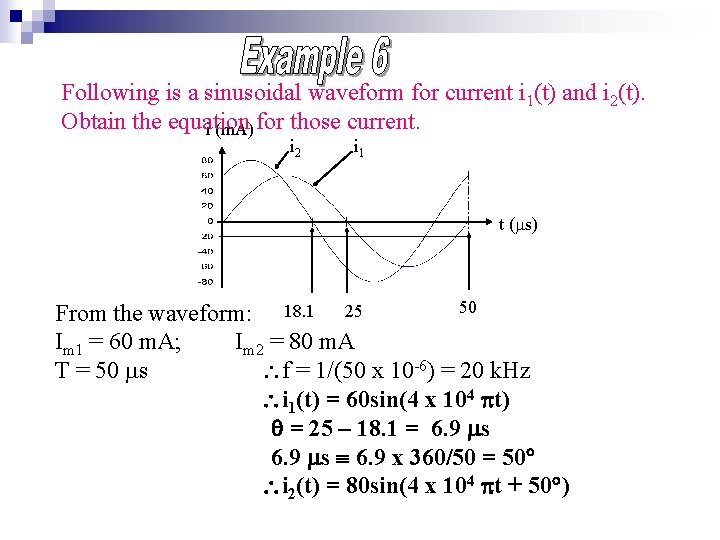
Following is a sinusoidal waveform for current i 1(t) and i 2(t). Obtain the equation i (m. A) for those current. i 2 i 1 t ( s) 50 From the waveform: 18. 1 25 Im 1 = 60 m. A; Im 2 = 80 m. A T = 50 s f = 1/(50 x 10 -6) = 20 k. Hz i 1(t) = 60 sin(4 x 104 t) = 25 – 18. 1 = 6. 9 s 6. 9 x 360/50 = 50 i 2(t) = 80 sin(4 x 104 t + 50 )

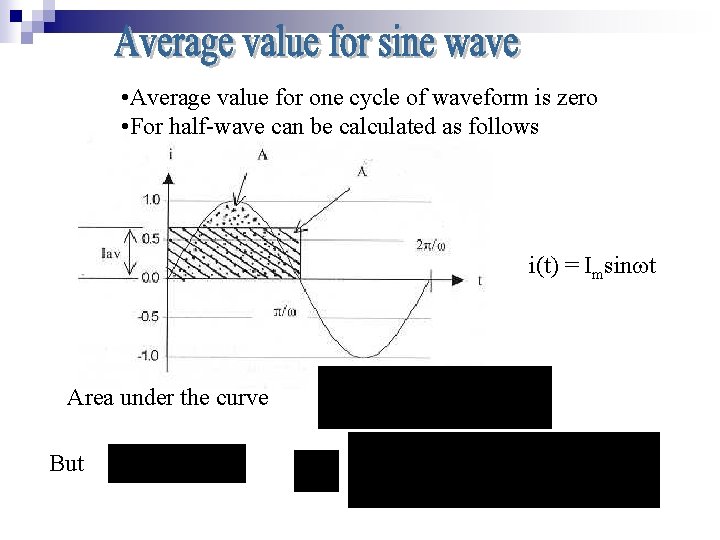
• Average value for one cycle of waveform is zero • For half-wave can be calculated as follows i(t) = Imsin t Area under the curve But

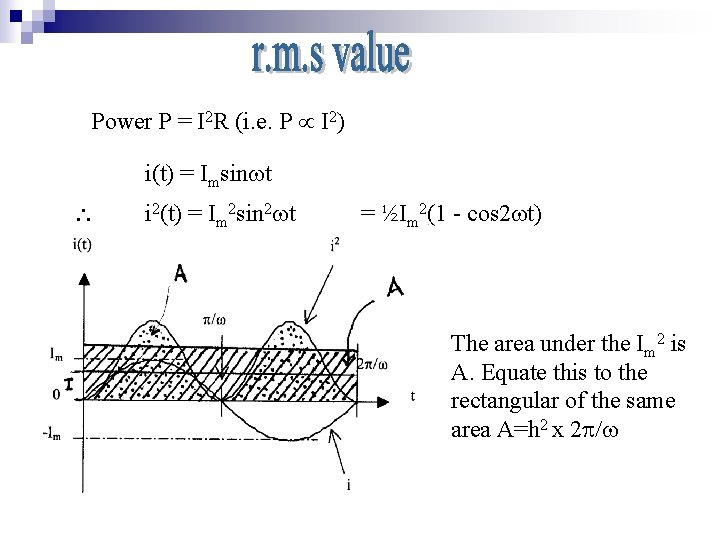
Power P = I 2 R (i. e. P I 2) i(t) = Imsin t i 2(t) = Im 2 sin 2 t = ½Im 2(1 - cos 2 t) The area under the Im 2 is A. Equate this to the rectangular of the same area A=h 2 x 2 /

Area under the Im 2 Height of the rectangular r. m. s value

An alternating current is given by an equation i(t)=0. 4 sin 100 t A; flowing into a resistor R=384 W for 48 hours. Calculate the energy in k. Wh consumed by the resistor. Im = 0. 4 I = 0. 707 x 0. 4 = 0. 283 A P = I 2 R = 0. 2832 x 384 = 30. 7 W W = Pt = 30. 7 x 48 = 1. 474 k. Wh

A sinusoidal voltage as in figure is applied to a resistor 56 W. Calculate the power absorbed by the resistor Power absorbed Vm = 339 V V = 0. 707 x 339 = 240 V P = V 2/R = 2402/56 = 1029 W

A purely resistive resistor of 17 W dissipates 3. 4 k. W when a sinusoidal voltage of frequency 50 Hz apply across it. Give an equation for the current passing through the resistor in a function of time. P = I 2 R or I = (P/R) = (3400/17) = 14. 14 A Im = I/0. 707 = 14. 14/0. 707 = 20 A = 2 f = 2 x 50 = 100 i(t) = Imsin t = 20 sin(100 t)

A moving –coil ammeter, a thermal ammeter and a rectifier are connected in series with a resistor across a 110 V sinusoidal a. c. supply. The circuit has a resistance of 50 W to current in one direction and , due to the rectifier, an infinity resistance to current in the reverse direction. Calculate : (1)The readings on the ammeters; (2)The form and peak factors of the current wave Initially the moving coil-ammeter will read the Iav for the first half of a cycle. The second half , the value of current will be zero (due to rectifier- reverse ). For the whole cycle, it will read 1. 98/2=0. 99 A

Thermal ammeter only response to the heat. This heat effect is corresponding to power dissipated in the resistor and given by the equation Full power is Since only half cycle give the heating effect, the other half is no current ( due to rectifier-reverse). Therefore the heating power will be thus Thus equivalent Irms read by the meter is

The actual value for full cycle is But only half a cycle then the reading is Form factor Peak factor

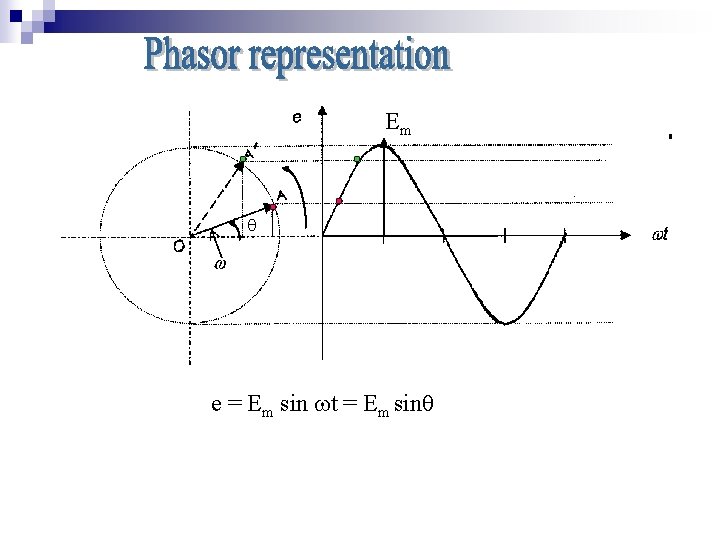
Em e = Em sin t = Em sin

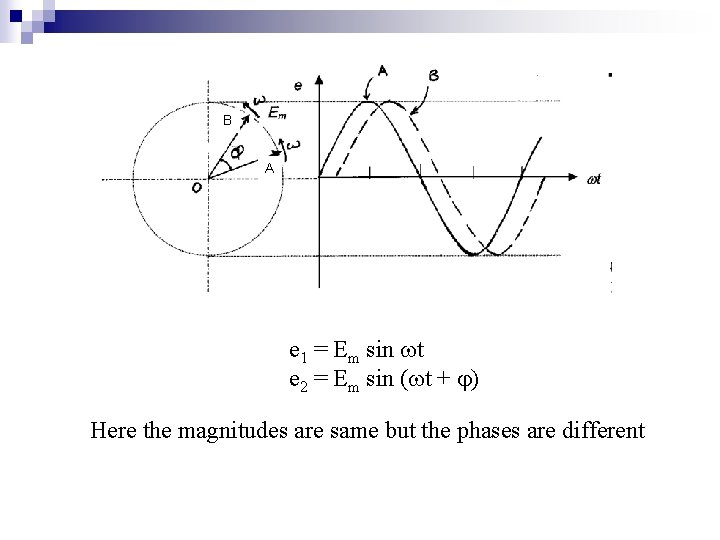
B A e 1 = Em sin t e 2 = Em sin ( t + ) Here the magnitudes are same but the phases are different

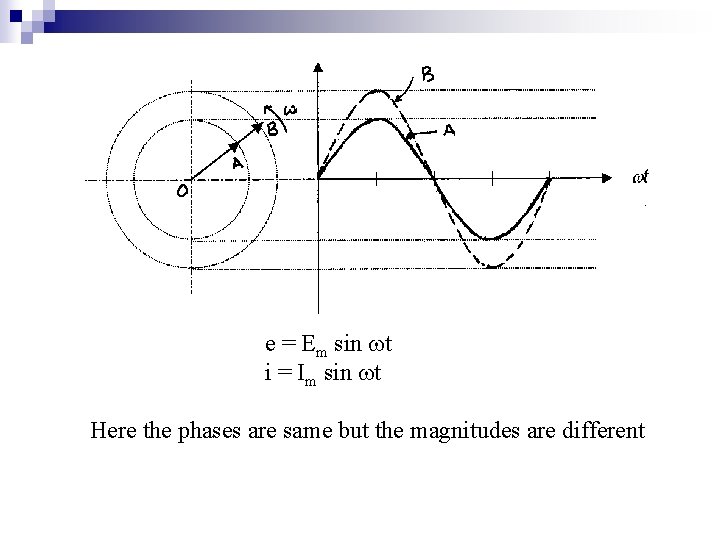
e = Em sin t i = Im sin t Here the phases are same but the magnitudes are different

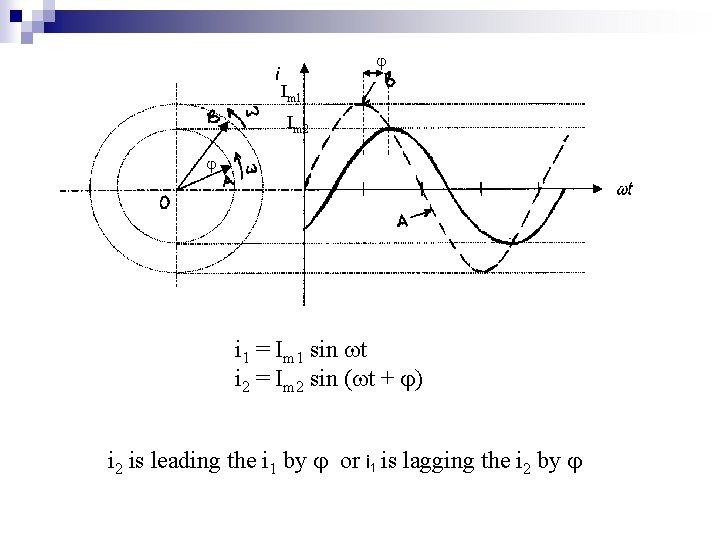
Im 1 Im 2 i 1 = Im 1 sin t i 2 = Im 2 sin ( t + ) i 2 is leading the i 1 by or i 1 is lagging the i 2 by

y CY A C AY Vertical components Ay = OA sin BY By = OB sin O Cy = Ay + By = OA sin + OB sin Horizontal components Ax = OA cos Bx = OB cos Cx = Ax + Bx = OA cos + OB cos Resultant = OC = (Cy 2 + Cx 2) B BX AX CX x

y Ay Cy A C -Bx Vertical components Ay = OA sin -B -By = -OB sin Cy = Ay - By = OA sin - OB sin Horizontal components Ax = OA cos -Bx = -OB cos Cx = Ax - Bx = OA cos - OB cos Resultant = OC = (Cy 2 + Cx 2) O -By Cx B Ax x

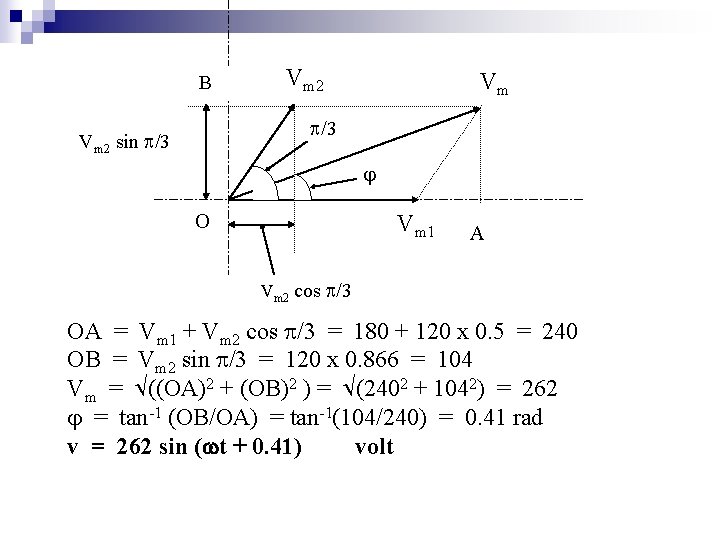
v 1 v 2 v Given v 1 = 180 sin 314 t volt ; and v 2 = 120 sin (314 t + /3) volt. Find 1. The supply voltage v in trigonometry form; 2. r. m. s voltage of supply 3. Supply frequency

B Vm 2 Vm /3 Vm 2 sin /3 O Vm 1 A Vm 2 cos /3 OA = Vm 1 + Vm 2 cos /3 = 180 + 120 x 0. 5 = 240 OB = Vm 2 sin /3 = 120 x 0. 866 = 104 Vm = ((OA)2 + (OB)2 ) = (2402 + 1042) = 262 = tan-1 (OB/OA) = tan-1(104/240) = 0. 41 rad v = 262 sin ( t + 0. 41) volt

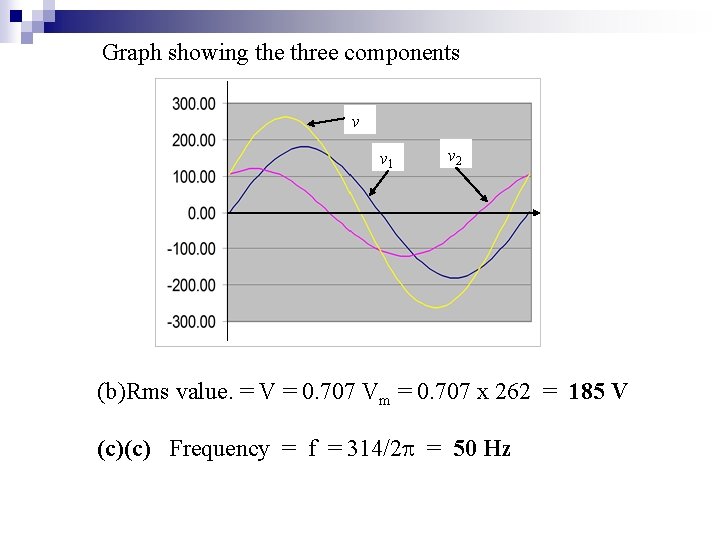
Graph showing the three components v v 1 v 2 (b)Rms value. = V = 0. 707 Vm = 0. 707 x 262 = 185 V (c)(c) Frequency = f = 314/2 = 50 Hz

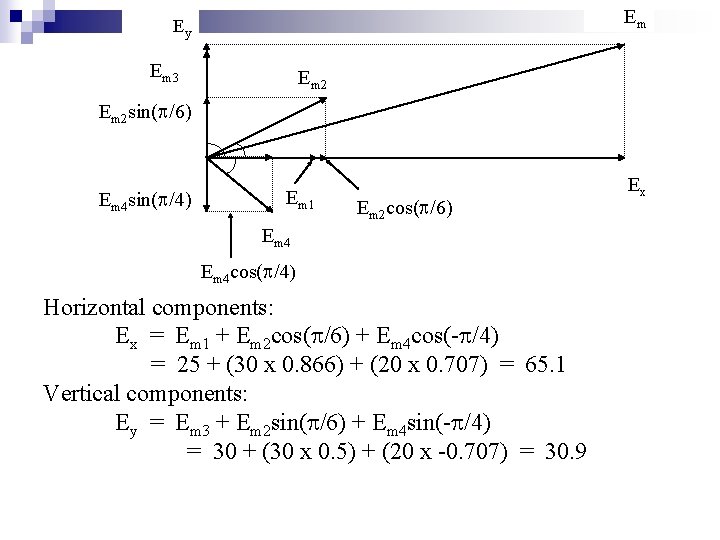
Find graphically or otherwise the resultants of the following voltages e 1 = 25 sin t, e 3 = 30 kos t, e 2 = 30 sin ( t + /6), e 4 = 20 sin ( t - /4) Express in the same form Solution e 1 e 2 e 3 e 4 = = 25 sin t [ V ] 30 sin ( t + /6) [ V ] 30 cos t [ V ] 20 sin ( t - /4) [ V ] Em 1 Em 2 Em 3 Em 4 = = 25 volt 30 volt 20 volt

Em Ey Em 3 Em 2 sin( /6) Em 4 sin( /4) Em 1 Em 2 cos( /6) Em 4 cos( /4) Horizontal components: Ex = Em 1 + Em 2 cos( /6) + Em 4 cos(- /4) = 25 + (30 x 0. 866) + (20 x 0. 707) = 65. 1 Vertical components: Ey = Em 3 + Em 2 sin( /6) + Em 4 sin(- /4) = 30 + (30 x 0. 5) + (20 x -0. 707) = 30. 9 Ex

Peak value for e: Em = (Ex 2 + Ey 2)½ = (65. 12+30. 92) ½ = 72 [V] Phase angle for e: = tan-1(Ey/Ex) = tan-1(30. 9/65. 1) = 25 = 5 /36 e = e 1 + e 2 + e 3 + e 4 = 72 sin( t + 5 /36)

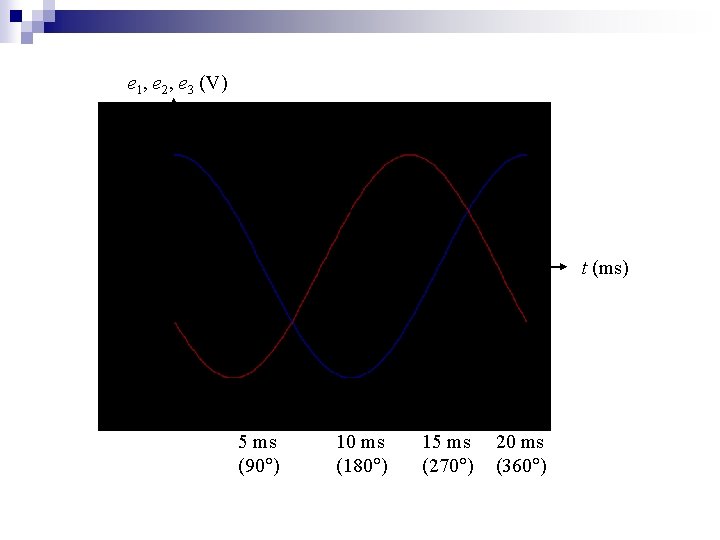
Show graphically the waveform and phasor diagrams of the resultant of the following voltages e = 339 cos 100 t + 339 cos(100 t + 120 ) + 339 cos(100 t + 240 ) What is the value of e? Say: e 1 = 339 cos 100 t, e 2 = 339 cos(100 t + 120 ), e 3 = 339 cos(100 t + 240 )

e 1, e 2, e 3 (V) e 1 e 2 e 3 t (ms) 5 ms (90 ) 10 ms (180 ) 15 ms (270 ) 20 ms (360 )

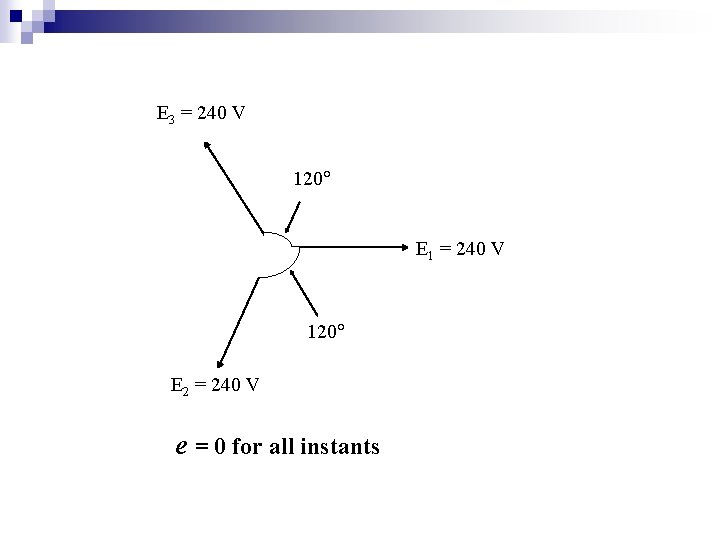
E 3 = 240 V 120 E 1 = 240 V 120 E 2 = 240 V e = 0 for all instants

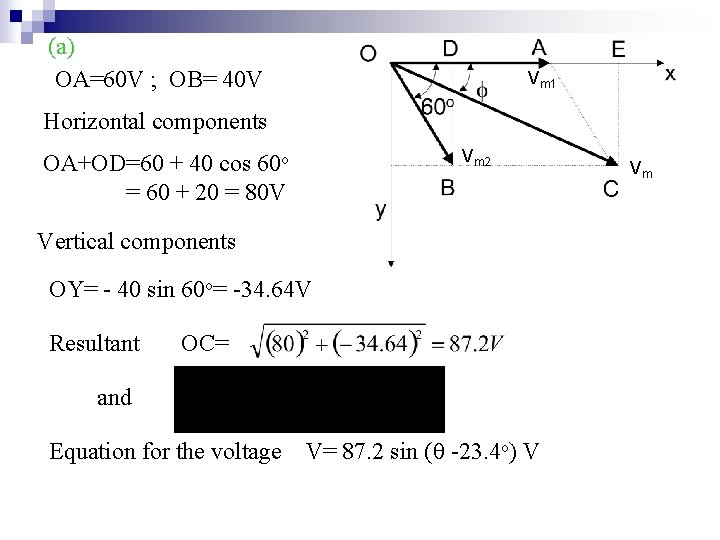
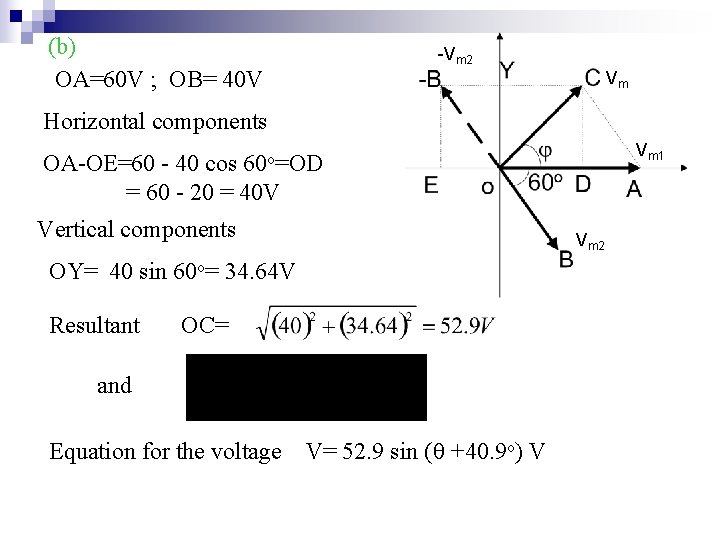
The instantaneous values of two alternating voltages are represented respectively by v 1=60 sin volts and v 2=40 sin( - /3) volts. Derive an expression for the instantaneous values of (a)The sum (b)The difference of these voltages. First we consider =0 or t=0 as reference in order to simplified the phasor diagram. Thus v 1 will be in the x-axis and v 2 will be – /3 or -60 o behind (lagging) v 1. Magnitude for v 1 is 60 V and v 2 is 40 V.

(a) OA=60 V ; OB= 40 V Vm 1 Horizontal components Vm 2 OA+OD=60 + 40 cos 60 o = 60 + 20 = 80 V Vertical components OY= - 40 sin 60 o= -34. 64 V Resultant OC= and Equation for the voltage V= 87. 2 sin ( -23. 4 o) V Vm

(b) OA=60 V ; OB= 40 V -Vm 2 Vm Horizontal components Vm 1 60 o=OD OA-OE=60 - 40 cos = 60 - 20 = 40 V Vertical components Vm 2 OY= 40 sin 60 o= 34. 64 V Resultant OC= and Equation for the voltage V= 52. 9 sin ( +40. 9 o) V