alo f buf cse Combining Numeric and Symbolic

alo f buf @ cse Combining Numeric and Symbolic Reasoning in SNe. PS Stuart C. Shapiro Department of Computer Science & Engineering Center for Multi. Source Information Fusion Center for Cognitive Science University at Buffalo, The State University of New York IF Workshop 2006 S. C. Shapiro

alo f buf @ cse SNe. PS is a Logic-Based Frame-Based Network-Based knowledge representation, reasoning, and acting system. 2 IF Workshop 2006 S. C. Shapiro

alo @ cse f buf This Talk • The logic-based view of SNe. PS • The SNe. PSLOG user interface. • The recently added procedural attachment to combine numeric with symbolic reasoning. 3 IF Workshop 2006 S. C. Shapiro

alo f buf @ cse Some SNe. PSLOG Syntax P(a, b) The proposition that P is true of a and b. P({a 1, …, an}, {b 1, …, bm}) The proposition that P is true of each ai and bj. andor(i, j){P 1, …, Pn} The proposition that at least i and at most j of the Pi are true. andor(1, 1){P 1, …, Pn} The proposition that exactly 1 of the Pi are true. andor(0, 0){P 1, …, Pn} The proposition that none of the Pi are true. ~P The proposition that P is false, abbreviation of andor(0, 0){P}. all(x, y, )(P(x, y) => Q(x, y)) The proposition that for every x and y, if P(x, y) then Q(x, y). all(x, y, )(P(x, y) => {Q 1(x, y), … Qn(x, y)}) The proposition that for every x and y, if P(x, y) then Qi(x, y), for each i. {P 1, …, Pn} &=> Q The conjunction of the Pi (solved in parallel) implies Q. P 1 => (… (Pn => Q)…) The conjunction of the Pi (solved in serial) implies Q. 4 IF Workshop 2006 S. C. Shapiro

alo f buf @ cse • • Procedural Attachment A predicate (proposition-forming function) symbol may be attached to a procedure so instances may be computed in the underlying programming language. 5 IF Workshop 2006 S. C. Shapiro

alo @ cse f buf Example of Procedural Attachment : Diff(7, 3, ? x)? wff 24!: Diff(7, 3, 4) : Diff(10, ? x, 7)? wff 25!: Diff(10, 3, 7) : Diff(? x, 5, 7)? wff 26!: Diff(12, 5, 7) : Diff(15, 8, 7)? wff 314!: Diff(15, 8, 7) : Diff(15, 8, 9)? wff 316!: ~Diff(15, 8, 9) 6 IF Workshop 2006 S. C. Shapiro

alo f buf @ cse Illustration Implementing a Bayesian Network in SNe. PS using combined symbolic and numeric reasoning 7 IF Workshop 2006 S. C. Shapiro

alo f buf @ cse Some Facts of Bayesian Probability in SNe. PSLOG P(x, p): Bel(x, p); calculated. Bel(x, p): The prior probability of x is p. The posterior probability of x is p. The calculated posterior probability of x is p. all(x, p)(P(x, p) => Bel(x, p)). all(x, p)(Bel(~x, p) => all(q)(Diff(1, p, q) => Bel(x, q))). all(x, y)(andor(1, 1){x, y} => all(p)(Bel(x, p) => all(q)(Diff(1, p, q) => Bel(y, q)))). all(x, p)(calculated. Bel(x, p) => Bel(x, p)). 8 IF Workshop 2006 S. C. Shapiro
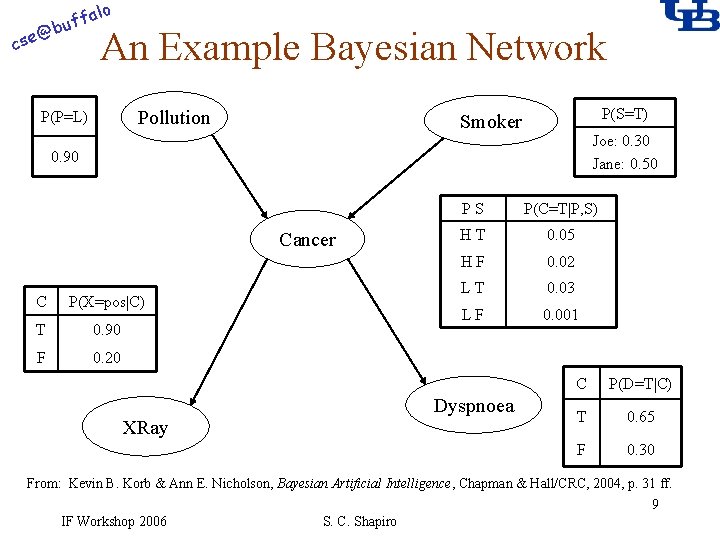
alo f buf @ cse An Example Bayesian Network Pollution P(P=L) P(S=T) Smoker Joe: 0. 30 Jane: 0. 50 0. 90 Cancer C P(X=pos|C) T 0. 90 F 0. 20 XRay PS P(C=T|P, S) HT 0. 05 HF 0. 02 LT 0. 03 LF 0. 001 Dyspnoea C P(D=T|C) T 0. 65 F 0. 30 From: Kevin B. Korb & Ann E. Nicholson, Bayesian Artificial Intelligence, Chapman & Hall/CRC, 2004, p. 31 ff. 9 IF Workshop 2006 S. C. Shapiro

alo f buf @ cse The Patient-Independent CPTs CP(x, y, p): JCP(x, y, z, p): Exposed. To(x, v, f): Does(x, a): Has(x, d): Positive(x): The conditional probability of x given y is p. The conditional probability of x given y and z is p. x has been exposed to a v level of factor f. x engages in the activity a. x has the disease d. The procedure x gave a positive result all(x)(andor(1, 1){Exposed. To(x, low, pollution), Exposed. To(x, high, pollution)}). all(x)(Patient(x) => {JCP(Has(x, cancer), Exposed. To(x, high, pollution), Does(x, smoke), 0. 05), JCP(Has(x, cancer), Exposed. To(x, high, pollution), ~Does(x, smoke), 0. 02), JCP(Has(x, cancer), Exposed. To(x, low, pollution), Does(x, smoke), 0. 03), JCP(Has(x, cancer), Exposed. To(x, low, pollution), ~Does(x, smoke), 0. 001), CP(Positive(X-ray(x)), Has(x, cancer), 0. 90), CP(Positive(X-ray(x)), ~Has(x, cancer), 0. 20), CP(Has(x, dyspnoea), Has(x, cancer), 0. 65), CP(Has(x, dyspnoea), ~Has(x, cancer), 0. 30)}). 10 IF Workshop 2006 S. C. Shapiro

alo @ cse f buf Algorithm for calculated. Bel Given an X, To find the p such that calculated. Bel(X, p): Infer from the KB all Ei, pi s. t. CP(X, Ei, pi). Infer from the KB the qi s. t. Bel(Ei, qi). Set pcp to Σi (pi * qi). Infer from the KB all E 1 i, E 2 i, pi s. t. JCP(X, E 1 i, E 2 i, pi). Infer from the KB the q 1 i s. t. Bel(E 1 i, q 1 i). and the q 2 i s. t. Bel(E 2 i, q 2 i). Set pjcp to Σi (pi * q 1 i * q 2 i). Set p to pcp + pjcp. 11 IF Workshop 2006 S. C. Shapiro

alo @ cse f buf The Patients and Their Priors Patient(x): x is a patient. Patient({Joe, Jane}). P(Exposed. To(Joe, low, pollution), 0. 90). P(Does(Joe, smoke), 0. 30). P(Exposed. To(Jane, low, pollution), 0. 90). P(Does(Jane, smoke), 0. 50). 12 IF Workshop 2006 S. C. Shapiro

alo @ cse f buf Inferring Posteriors : Bel(Exposed. To(Joe, low, pollution), ? p)? wff 12!: Bel(Exposed. To(Joe, low, pollution), 0. 9) : Bel(~Does(Joe, smoke), ? p)? wff 32!: Bel(~Does(Joe, smoke), 0. 7) : Bel(Exposed. To(Joe, high, pollution), ? p)? wff 46!: Bel(Exposed. To(Joe, high, pollution), 0. 1) : Bel(Has(Joe, cancer), ? p)? wff 90!: Bel(Has(Joe, cancer), 0. 011) : Bel(Positive(X-ray(Joe)), ? p)? wff 104!: Bel(Positive(X-ray(Joe)), 0. 208) : Bel(Has(Joe, dyspnoea), ? p)? wff 126!: Bel(Has(Joe, dyspnoea), 0. 304) ; should be 0. 9 : Bel(Has(Jane, cancer), ? p)? wff 280!: Bel(Has(Jane, cancer), 0. 017) : Bel(Positive(X-ray(Jane)), ? p)? wff 294!: Bel(Positive(X-ray(Jane)), 0. 212) : Bel(Has(Jane, dyspnoea), ? p)? wff 377!: Bel(Has(Jane, dyspnoea), 0. 306) ; should be 0. 017 ; should be 0. 1 ; should be 0. 011 ; should be 0. 208 ; should be 0. 304 ; should be 0. 212 ; should be 0. 306 13 IF Workshop 2006 S. C. Shapiro

alo f buf @ cse Conclusions • SNe. PS uses procedural attachment combine numeric with symbolic reasoning. to – New attached procedures may be added by the KE. • Strengths of symbolic reasoning: – Representation of, and reasoning about general cases. – Instantiating multiple specific cases. – Clarity of declarative statements. • Strengths of numerical reasoning: – Complicated numerical calculations. – Especially sums and products of series. – Sometimes faster than logical deduction. 14 IF Workshop 2006 S. C. Shapiro
- Slides: 14