AlMustansiriyah University Faculty of Engineering Elec Eng Department

Al-Mustansiriyah University Faculty of Engineering Elec. Eng. Department Electric Circuits Second Year Class Dr. Eng. Ammar Ali Sahrab 1. Complex Numbers: There are two ways to designate a complex number, with Cartesian or rectangular form or with polar or trigonometric form. In rectangular form a complex number is written in terms of its real and imaginary components. Z a jb. . . (1) Where a=real component, b=imaginary component, and j 1. In polar form complex number is written in terms of its magnitude (or modulus) and angle (or argument) components. . (2) Z cej Where c=magnitude component, =angle component, and e=exponential. The symbol is frequently used instead of e j , so: Z c O. . . (3) The transition from polar to rectangular form makes use of Euler’s identity. e j cos jsin . . . (4) j ce c(cos jsin ) a jb or a c cos and b c sin Note: The sine function is odd ( sin( ) sin ) and the cosine function is even ( cos( ) cos ). The transition from rectangular to polar form makes use of geometry of right triangle. a jb a 2 b 2 e j ce j or b c a 2 b 2 and tan 1 a 2. The Graphical Representation of a Complex Number: A complex number is represented graphically on a complex number plane, which uses the horizontal axis for plotting the real component and the vertical axis for plotting the imaginary component. The angle of the complex number is measured counterclockwise from the positive real axis. The distance from origin to that point on complex plane represents magnitude (c). Imaginary Axis b Z c O Real a Axis Complex Plane Example: Draw the graphical representation of a complex number Z=4+j 3. Im 3 Solution: c a b 4 3 5 b 3 tan 1 4 36. 87 O a 2 2 Z 5 36. 87 O 4 Re Note: The conjugate of a complex number is formed by reversing the sign of its imaginary component. Thus the conjugate of a+jb is ajb, and the conjugate of -a+jb is -a-jb. In polar form the conjugate is formed by reversing the sign of the angle . Therefore the conjugate of c O is c O. Chapter 1: Vector Diagram -1 -

Al-Mustansiriyah University Faculty of Engineering Elec. Eng. Department Electric Circuits Second Year Class Dr. Eng. Ammar Ali Sahrab HW: Convert (Express) the following complex numbers in polar form. -6+j 8, 1 -j, 3 -j 6, -10 -j 10 & -2. 3+j 8. 1 3. Arithmetic Operations on a Complex Numbers: a. Addition and Subtraction: To add or subtract complex numbers, the number must be expressed in rectangular form. if Z 1 a 1 jb 1 and Z 2 a 2 jb 2 then: Z 1 Z 2 (a 1 a 2 ) j(b 1 b 2 ) and Z 1 Z 2 (a 1 a 2 ) j(b 1 b 2 ) Example: Add and subtract the following two complex numbers Z 1 8 j 16 Z 2 12 j 3. and Solution: Addition, Z 1 Z 2 (8 12) j(16 3) 20 j 13 Subtraction, Z 2 Z 1 (12 8) j( 3 16) 4 j 19 Note: If the complex numbers are given in polar form, they are converted to rectangular form. Example: Add and subtract the following two complex numbers Z 1 10 53. 13 O and Z 2 5 135 O. Solution: Addition, Z 1 Z 2 10 53. 13 O 5 135 O 6 j 8 3. 535 j 3. 535 2. 465 j 4. 465 5. 1 61. 1 O Subtraction, O O O Z 1 Z 2 10 53. 13 5 135 6 j 8 3. 535 j 3. 535 9. 535 j 11. 535 14. 966 50. 42 b. Multiplication and Division: Multiplication and division of complex numbers can be carried out with numbers in rectangular or polar form. if Z 1 a 1 jb 1 and Z 2 a 2 jb 2 then: Z 1 Z 2 c 1 c 2 1 o 2 o (a 1 a 2 b 1 b 2 ) j(a 1 b 2 a 2 b 1) Z 1 c 1 o o (a 1 a 2 b 1 b 2 ) j (a 2 b 1 a 1 b 2 ) algebraic addition and subtraction of angles 1 2 2 2 Z 2 c 2 a 2 b 2 Example: Multiply and Divide the following two complex numbers Z 1 8 j 10 and Z 2 5 j 4. Solution: Multiplication, Z 1 Z 2 (8 j 10)(5 j 4) 80 j 18 82 12. 68 O 0 j 82 0 j 2 2 90 O 41 ((5 j 4))(5 j 4) Division, Z 1 8 j 10 (8 j 10)(5 j 4) Z 2 5 j 4 Example: Multiply and Divide the following two complex numbers O O Z 1 10 53. 13 and Z 2 5 135. Solution: Multiplication, Z Z (10 53. 13 O )(5 135 O ) 50 81. 87 O 7. 071 j 49. 498 1 2 Chapter 1: Vector Diagram -2 -

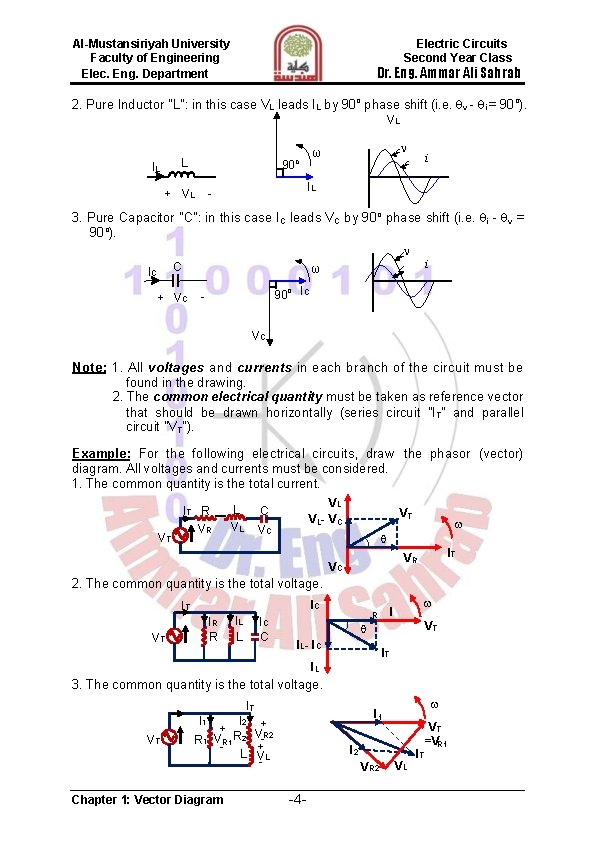
Al-Mustansiriyah University Faculty of Engineering Elec. Eng. Department Electric Circuits Second Year Class Dr. Eng. Ammar Ali Sahrab O Division, Z 1 10 53. 13 O 2 188. 13 O 1. 98 j 0. 283 Z 2 5 135 c. Useful Identities: In working with complex numbers and quantities, the following identities are very useful. j 2 m 1 or ( j)(j) 1 1 j j 1 or e j / 2 j e j ZZ* a 2 b 2 c 2 or Z / Z* 1 2 O Z Z* 2 a or Z Z* j 2 b n k (a jb)k c k e jk c k (cos k jsin k ) HW: Multiply and Divide the following two complex numbers and find the polar and rectangular forms: Z 1 7 j 7 and Z 2 8 j 6 4. Phasor (Voltage) Diagram: The terms “lead” and “lag” as well as “in-phase” and “out-of-phase” were used to indicate the relationship of one waveform to the other with the generalized sinusoidal expression given as: A(t) = A m sin(ωt ± ) representing the in the time-domain form. sinusoid v v(t) = Vm sin(ωt ± v) and i(t) = I m sin(ωt ± i) lead ω where ω is the radian angular frequency (rad/sec) =2 f and f is the frequency of the wave (Hz) =1/T (T is the i lag period for complete one wave cycle) v i after t seconds the displacement angle is 0 2 ωt=2 ft= t = , so sin =sinωt which is called Hz=Cycle/sec T frequency domain. Note: v and i are not conditionally the same value that depend on circuit elements. Vector: It is a complex number in polar or rectangular form has an arrow head at one end which signifies partly the maximum value of the vector quantity (V or I) and partly the end of the vector rotate in angular frequency ω. 1. Pure Resistance "R": in this case there is no phase shift between V R and IR (i. e. v = i). IR ω R + VR - Chapter 1: Vector Diagram IR -3 - VR i

Al-Mustansiriyah University Faculty of Engineering Elec. Eng. Department Electric Circuits Second Year Class Dr. Eng. Ammar Ali Sahrab 2. Pure Inductor "L": in this case VL leads IL by 90 o phase shift (i. e. v - i = 90 o). VL L IL 90 + VL ω o i IL - 3. Pure Capacitor "C": in this case IC leads VC by 90 o phase shift (i. e. i - v = 90 o). C IC i ω + VC 90 o IC VC Note: 1. All voltages and currents in each branch of the circuit must be found in the drawing. 2. The common electrical quantity must be taken as reference vector that should be drawn horizontally (series circuit "IT" and parallel circuit "VT"). Example: For the following electrical circuits, draw the phasor (vector) diagram. All voltages and currents must be considered. 1. The common quantity is the total current. VT IT R VR L VL VL VL- V C C VC VT IT VR VC 2. The common quantity is the total voltage. IC IT IR R VT IL L IC C I R VT IL- IC IT IL 3. The common quantity is the total voltage. IT I 1 VT I 2 + + R R 1 VR 1 2 V-R 2 + L VL - Chapter 1: Vector Diagram I 1 I 2 VR 2 -4 - VL IT VT =VR 1

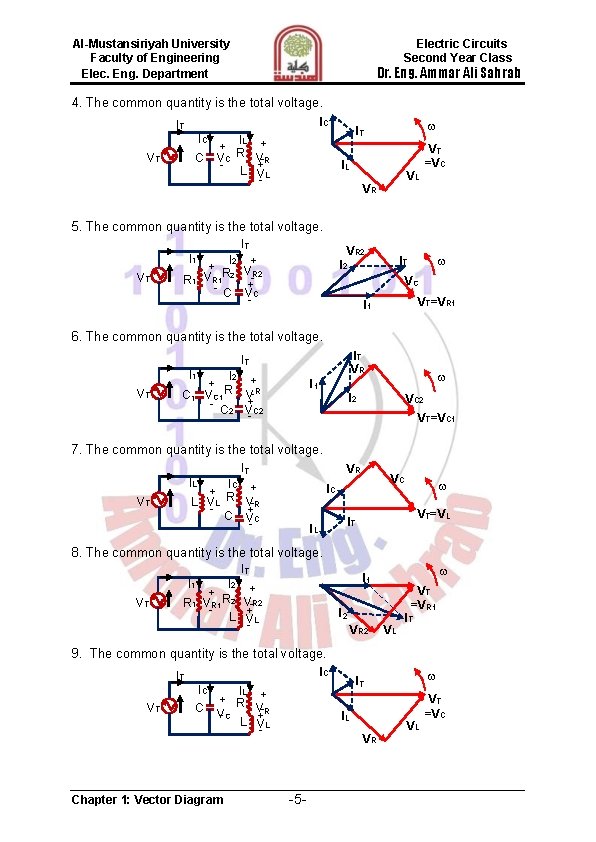
Al-Mustansiriyah University Faculty of Engineering Elec. Eng. Department Electric Circuits Second Year Class Dr. Eng. Ammar Ali Sahrab 4. The common quantity is the total voltage. IC IT IC VT C IL + R + V-R VC + L V -L IT IL VL VR VT =VC 5. The common quantity is the total voltage. IT I 1 VT VR 2 I 2 + R V+R 2 VR 1 2 + - C V C - R 1 IT I 2 VC VT=VR 1 I 1 6. The common quantity is the total voltage. IT VR IT I 1 VT I 2 + + R V-R VC 1 + - C 2 V C 2 - C 1 I 2 VC 2 VT=VC 1 7. The common quantity is the total voltage. IT VR IL IC + R + V-R L VL + C VC - VT VC IC VT=V L IT IL 8. The common quantity is the total voltage. IT I 1 VT I 1 I 2 + + R R 1 VR 1 2 V-R 2 + L VL - VT =VR 1 I 2 VR 2 VL IT 9. The common quantity is the total voltage. IC IT IC VT C IL + R + V-R V- C + L V -L Chapter 1: Vector Diagram IL VR -5 - IT VL VT =VC

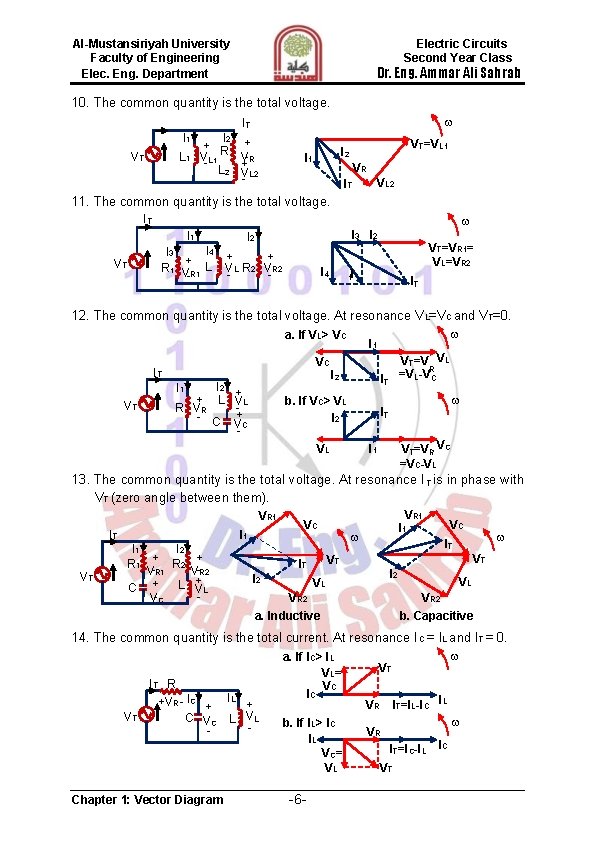
Al-Mustansiriyah University Faculty of Engineering Elec. Eng. Department Electric Circuits Second Year Class Dr. Eng. Ammar Ali Sahrab 10. The common quantity is the total voltage. IT I 1 VT L 1 I 2 + R + V-R VL 1 L 2 + V - L 2 VT=VL 1 I 2 I 1 VR IT VL 2 11. The common quantity is the total voltage. IT VT I 3 I 2 I 1 I 2 I 4 I 3 + + + R 1 VR 1 L V L R 2 VR 2 - I 4 VT=VR 1= VL=VR 2 1 I IT 12. The common quantity is the total voltage. At resonance V L=VC and VT=0. a. If VL> VC VC IT I 2 + + L VL R VR - C + VC I 1 VT I 1 I 2 VT=V VL =VL-VRC IT b. If VC> VL I 2 IT VT=VR VC =VC-VL I 1 VL 13. The common quantity is the total voltage. At resonance I T is in phase with VT (zero angle between them). VR 1 IT VT I 1 I 2 I 1 + + R 2 R 1 V-R 2 V-R 1 + L V C + L V- C VR 1 VC IT VT VT IT I 2 VC I 1 I 2 VL VL VR 2 b. Capacitive a. Inductive 14. The common quantity is the total current. At resonance I C = IL and IT = 0. VT IT R +VR - IC + IL + C VC L VL - Chapter 1: Vector Diagram a. If IC> IL VL= VC IC b. If IL> IC IL VC = VL -6 - VT IT=IL-IC IL VR VR IT=IC-IL VT IC

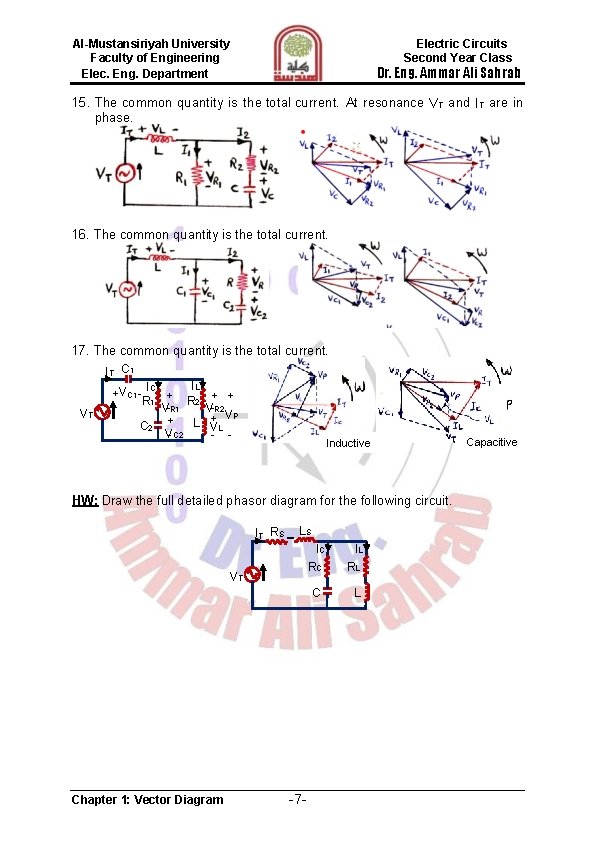
Al-Mustansiriyah University Faculty of Engineering Elec. Eng. Department Electric Circuits Second Year Class Dr. Eng. Ammar Ali Sahrab 15. The common quantity is the total current. At resonance VT and IT are in phase. 16. The common quantity is the total current. 17. The common quantity is the total current. IT C 1 IL IC + R 2 + + R 1 V-R 2 VR 1 + VP L V C 2 + L V- C 2 - - +VC 1 VT Inductive HW: Draw the full detailed phasor diagram for the following circuit. IT RS LS VT Chapter 1: Vector Diagram -7 - IC RC IL RL C L Capacitive