AllPairs Shortest Paths Find the distance between every

All-Pairs Shortest Paths • Find the distance between every pair of vertices in a weighted graph G.

All-Pairs Shortest Paths • We can make n calls to Dijkstra’s algorithm – O(n(n+m)log n) time From A one may reach C faster by reaching by traveling from A to B and then from B to C. Alternatively. . . Use dynamic programming: The Floyd’s Algorithm O(n 3) time.

Floyd’s Shortest Path Algorithm • Idea #1: Number the vertices 1, 2, …, n. • Idea #2: Shortest path between vertex i and vertex j without passing through any other vertex is weight(edge(i, j)). – Let it be D 0(i, j). • Idea #3: If Dk(i, j) is the shortest path between vertex i and vertex j using vertices numbered 1, 2, …, k, as intermediate vertices, then Dn(i, j) is the solution to the shortest path problem between vertex i and vertex j.

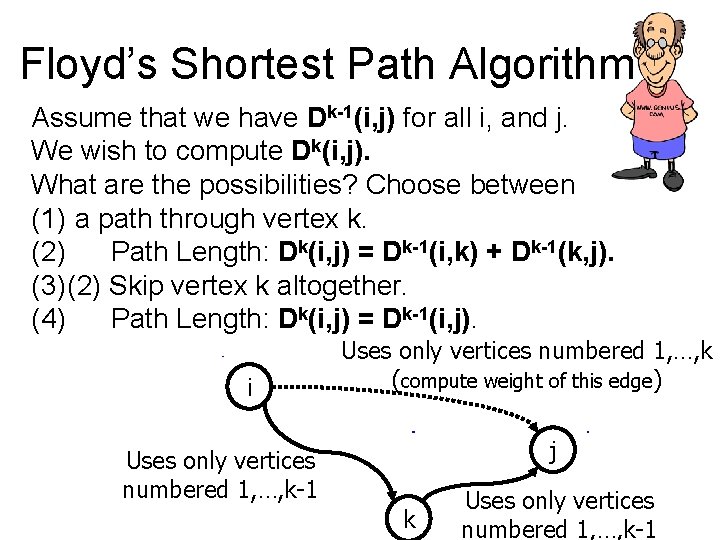
Floyd’s Shortest Path Algorithm Assume that we have Dk-1(i, j) for all i, and j. We wish to compute Dk(i, j). What are the possibilities? Choose between (1) a path through vertex k. (2) Path Length: Dk(i, j) = Dk-1(i, k) + Dk-1(k, j). (3) (2) Skip vertex k altogether. (4) Path Length: Dk(i, j) = Dk-1(i, j). i Uses only vertices numbered 1, …, k (compute weight of this edge) j Uses only vertices numbered 1, …, k-1 k Uses only vertices numbered 1, …, k-1

Floyd’s Shortest Path Algorithm i Uses only vertices numbered 1, …, k (compute weight of this edge) Uses only vertices numbered 1, …, k-1 j k Uses only vertices numbered 1, …, k-1

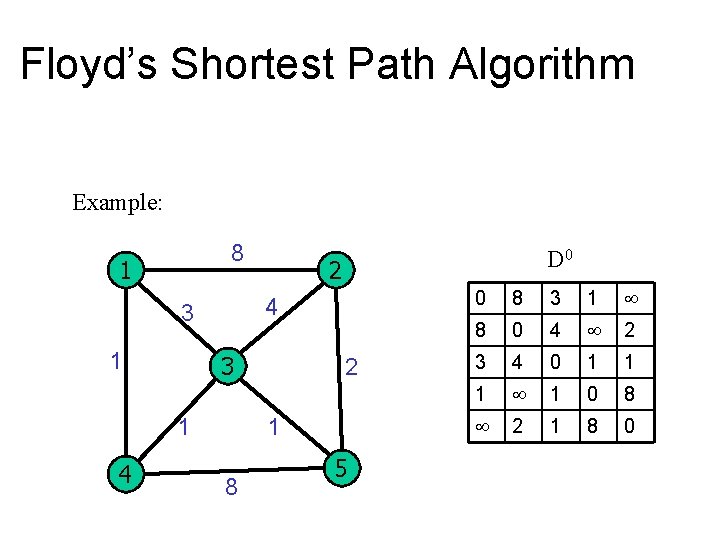
Floyd’s Shortest Path Algorithm Example: 8 1 3 1 4 2 4 3 1 D 0 2 1 8 5 0 8 3 1 8 0 4 2 3 4 0 1 1 0 8 2 1 8 0

Floyd’s Shortest Path Algorithm Example: 8 1 3 1 4 2 4 3 1 D 1 2 1 8 5 0 8 3 1 8 0 4 9 2 3 4 0 1 1 1 9 1 0 8 2 1 8 0

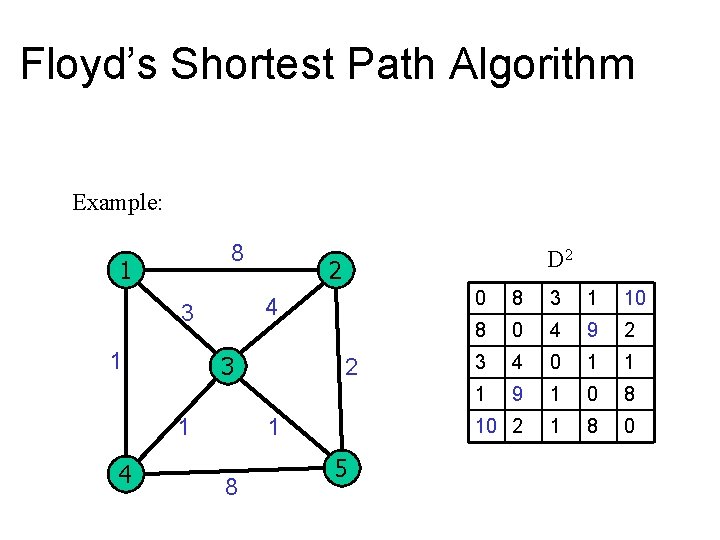
Floyd’s Shortest Path Algorithm Example: 8 1 3 1 4 2 4 3 1 D 2 2 1 8 5 0 8 3 1 10 8 0 4 9 2 3 4 0 1 1 1 9 1 0 8 10 2 1 8 0

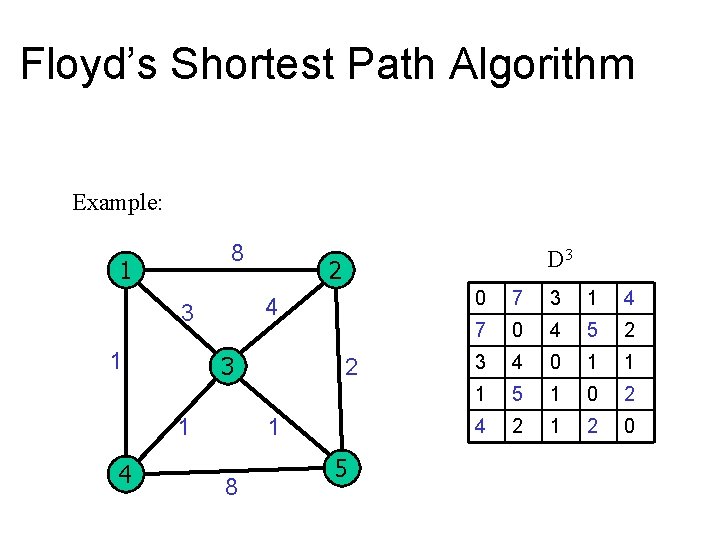
Floyd’s Shortest Path Algorithm Example: 8 1 3 1 4 2 4 3 1 D 3 2 1 8 5 0 7 3 1 4 7 0 4 5 2 3 4 0 1 1 1 5 1 0 2 4 2 1 2 0

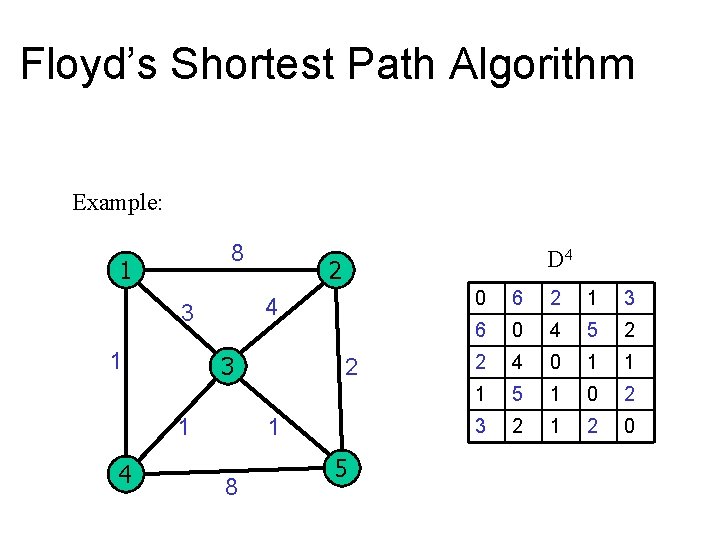
Floyd’s Shortest Path Algorithm Example: 8 1 3 1 4 2 4 3 1 D 4 2 1 8 5 0 6 2 1 3 6 0 4 5 2 2 4 0 1 1 1 5 1 0 2 3 2 1 2 0

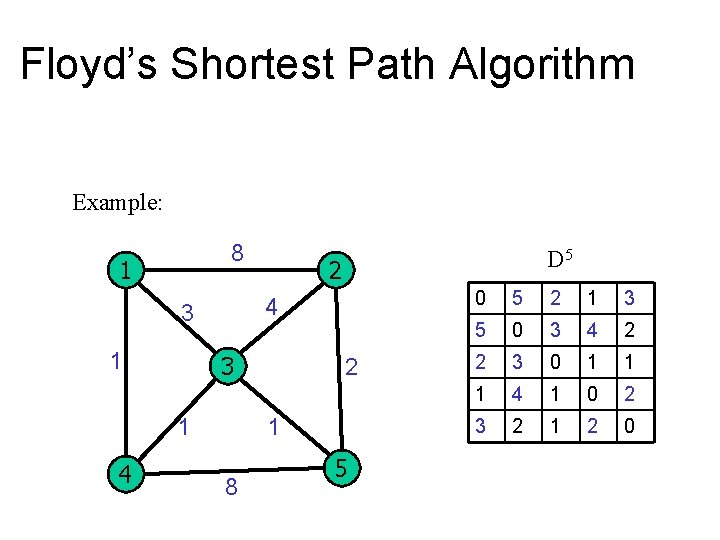
Floyd’s Shortest Path Algorithm Example: 8 1 3 1 4 2 4 3 1 D 5 2 1 8 5 0 5 2 1 3 5 0 3 4 2 2 3 0 1 1 1 4 1 0 2 3 2 1 2 0

Floyd’s Shortest Path Algorithm All. Pair(G) {assumes vertices 1, …, n} for all vertex pairs (i, j) if i = j O(n+m) 0 d [i, i] 0 or else if (i, j) is an edge in G O(n 2) 0 d [i, j] weight of edge (i, j) else d 0[i, j] + for k 1 to n do for i 1 to n do 3) O(n for j 1 to n do dk[i, j] min(dk-1[i, j], dk-1[i, k]+dk-1[k, j])

Floyd’s Shortest Path Algorithm Observation: dk [i, k] = dk-1[i, k] dk[k, j] = dk-1[k, j]

Floyd’s Shortest Path Algorithm All. Pair(G) {assumes vertices 1, …, n} for all vertex pairs (i, j) if i = j d[i, i] 0 else if (i, j) is an edge in G d[i, j] weight of edge (i, j) else d[i, j] + for k 1 to n do for i 1 to n do for j 1 to n do d[i, j] min(d[i, j], d[i, k]+d[k, j])

Floyd’s Shortest Path Algorithm All. Pair(G) {assumes vertices 1, …, n} for all vertex pairs (i, j) path[i, j] null if i = j d[i, i] 0 else if (i, j) is an edge in G d[i, j] weight of edge (i, j) else d[i, j] + for k 1 to n do for i 1 to n do for j 1 to n do if (d[i, k]+d[k, j] < d[i, j]) path[i, j] vertex k d[i, j] d[i, k]+d[k, j]

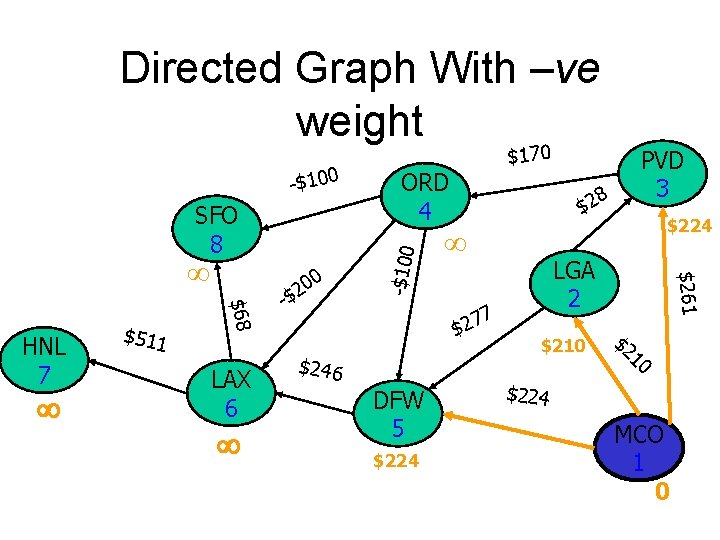
Floyd’s Shortest Path Algorithm • Can be applied to Directed Graphs • Can accept –ve edges as long as there are no –ve cycles.

Transitive Closure • Transitive Relation: A relation R on a set A is called transitive if and only if for any a, b, and c in A, whenever <a, b> R , and <b, c> R , <a, c> R

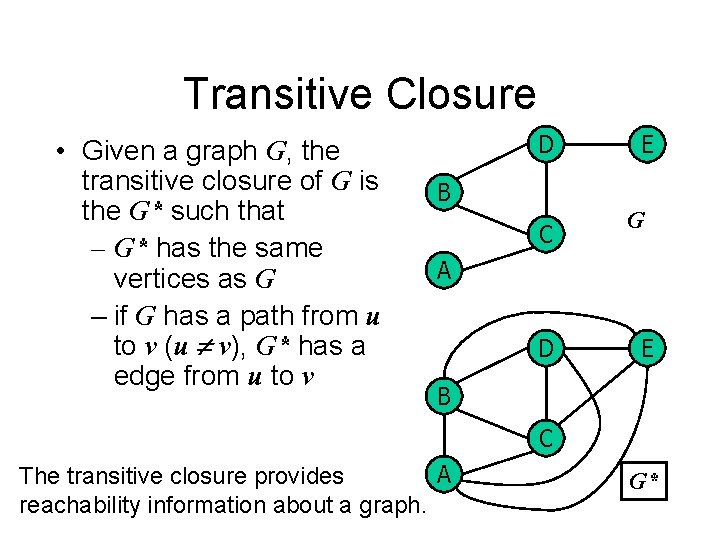
Transitive Closure • Given a graph G, the transitive closure of G is the G* such that – G* has the same vertices as G – if G has a path from u to v (u v), G* has a edge from u to v D E B C G A D E B C A The transitive closure provides reachability information about a graph. G*

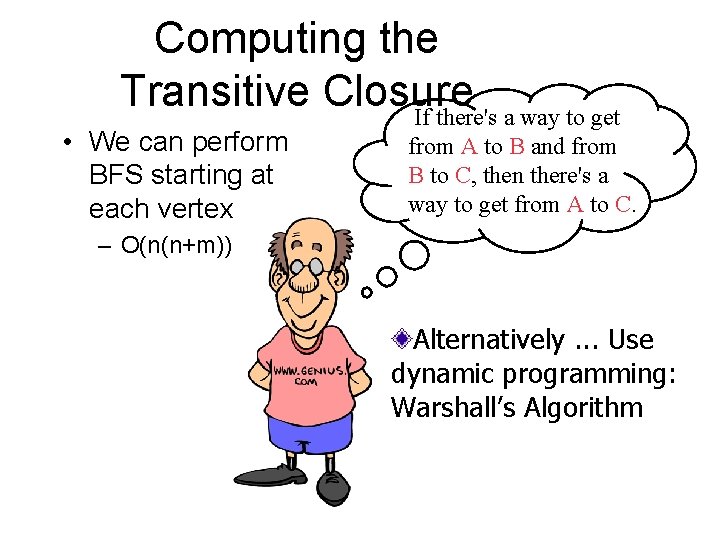
Computing the Transitive Closure If there's a way to get • We can perform BFS starting at each vertex from A to B and from B to C, then there's a way to get from A to C. – O(n(n+m)) Alternatively. . . Use dynamic programming: Warshall’s Algorithm

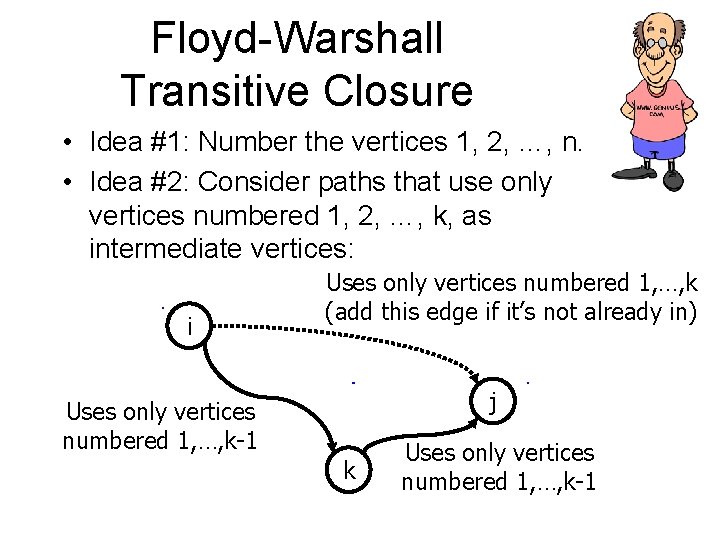
Floyd-Warshall Transitive Closure • Idea #1: Number the vertices 1, 2, …, n. • Idea #2: Consider paths that use only vertices numbered 1, 2, …, k, as intermediate vertices: i Uses only vertices numbered 1, …, k (add this edge if it’s not already in) j Uses only vertices numbered 1, …, k-1 k Uses only vertices numbered 1, …, k-1

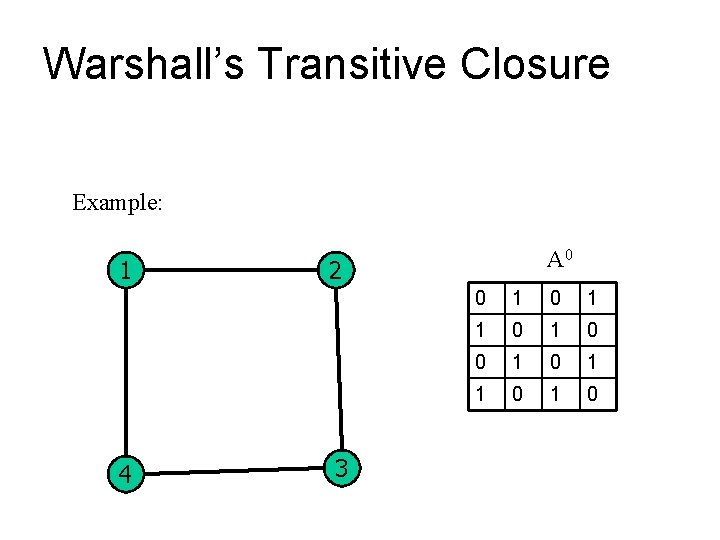
Warshall’s Transitive Closure Example: 1 4 A 0 2 3 0 1 0 1 0

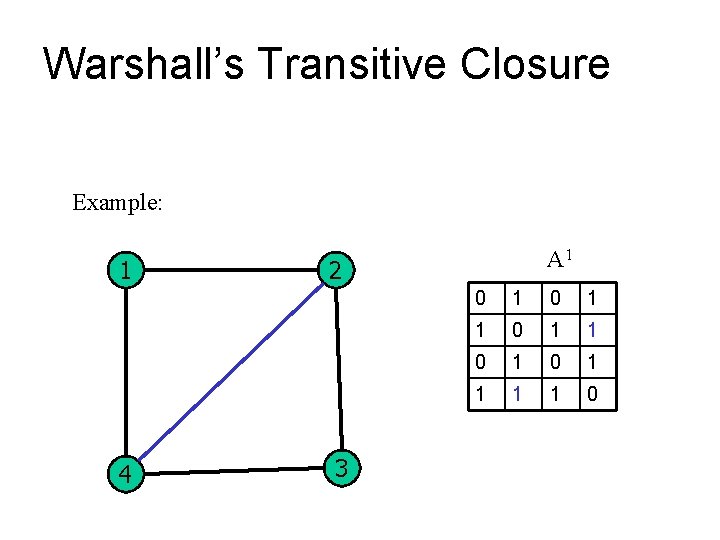
Warshall’s Transitive Closure Example: 1 4 A 1 2 3 0 1 1 0 1 0 1 1 0

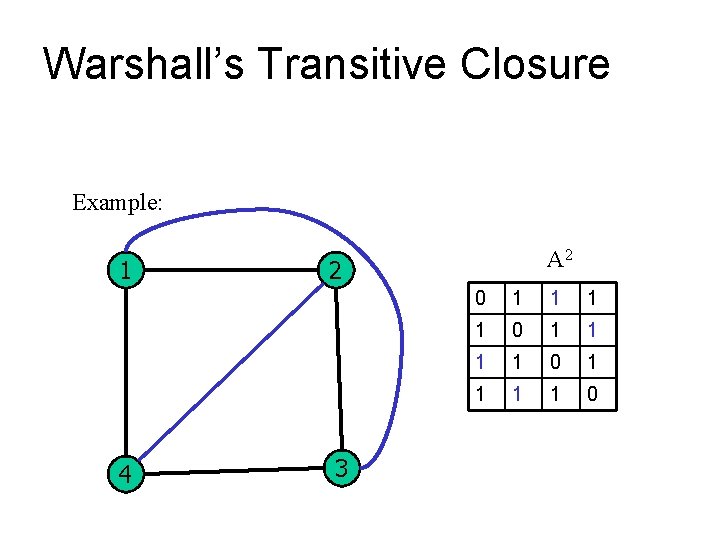
Warshall’s Transitive Closure Example: 1 4 A 2 2 3 0 1 1 1 1 0

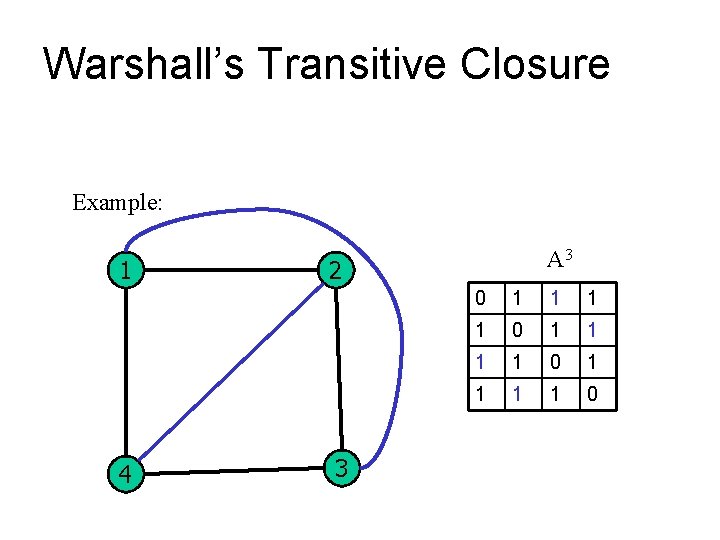
Warshall’s Transitive Closure Example: 1 4 A 3 2 3 0 1 1 1 1 0

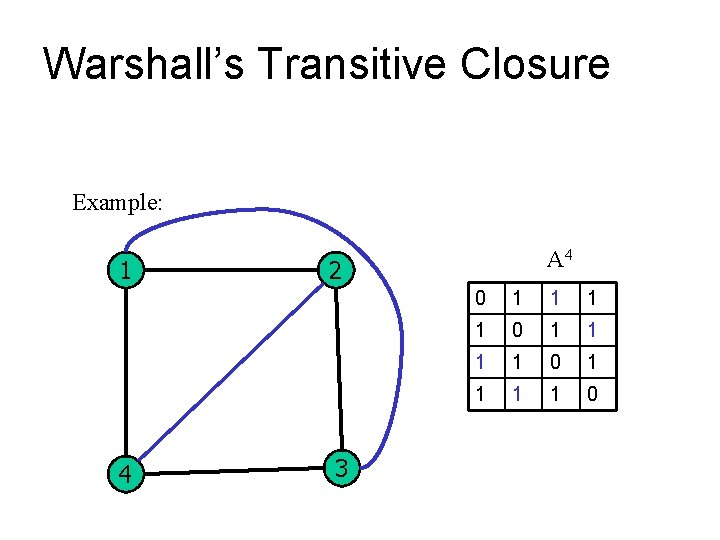
Warshall’s Transitive Closure Example: 1 4 A 4 2 3 0 1 1 1 1 0

Warshall’s Algorithm • Warshall’s algorithm numbers Algorithm Floyd. Warshall(G) Input graph G the vertices of G as v 1 , …, vn Output transitive closure G* of G and computes a series of i 1 graphs G 0, …, Gn – G 0=G – Gk has a edge (vi, vj) if G has a path from vi to vj with intermediate vertices in the set {v 1 , …, vk} • We have that Gn = G* • In phase k, graph Gk is computed from Gk - 1 • Running time: O(n 3), assuming are. Adjacent is O(1) (e. g. , adjacency matrix) for all v G. vertices() denote v as vi i i+1 G 0 G for k 1 to n do Gk - 1 for i 1 to n (i k) do for j 1 to n (j i, k) do if Gk - 1. are. Adjacent(vi, vk) Gk - 1. are. Adjacent(vk, vj) if Gk. are. Adjacent(vi, vj) Gk. insert. Edge(vi, vj , k) return Gn

Shortest Path Algorithm for DAGs • Use Dijkstra’s algorithm – Time: O((n+m) log n) • Use Topological sort based algorithm – Time: O(n+m).

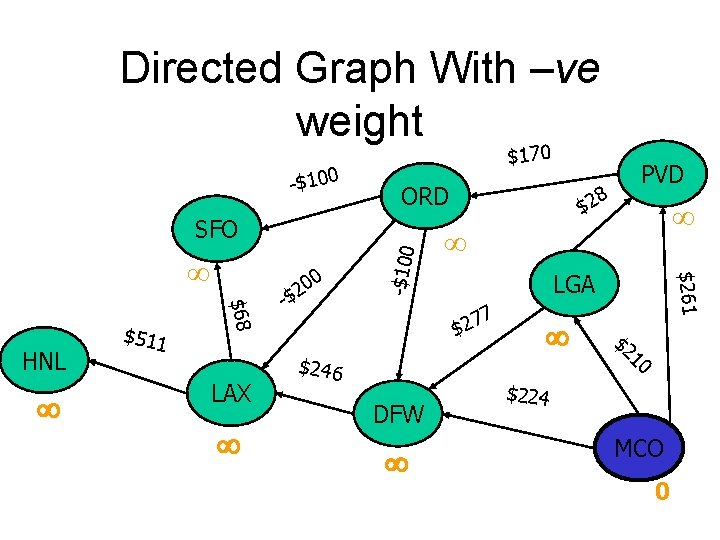
Directed Graph With –ve weight -$100 $170 ORD $68 HNL $511 LAX 0 - 0 2 $ 8 $2 LGA 7 7 2 $ $246 DFW $261 -$100 SFO PVD $2 10 $224 MCO 0

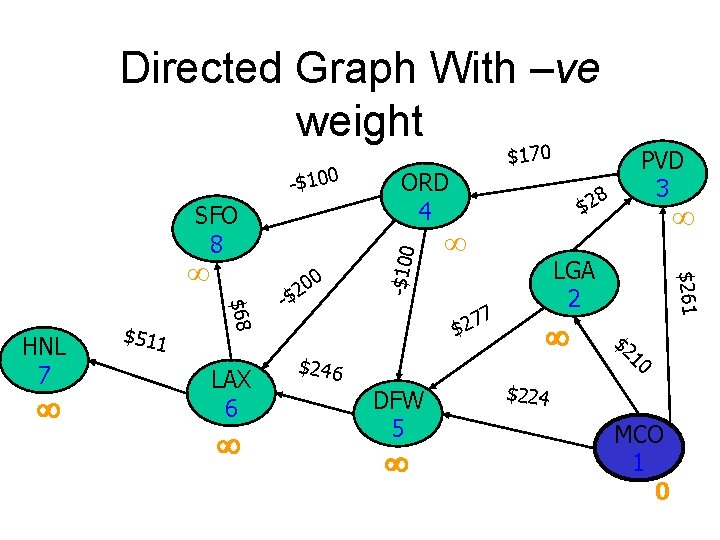
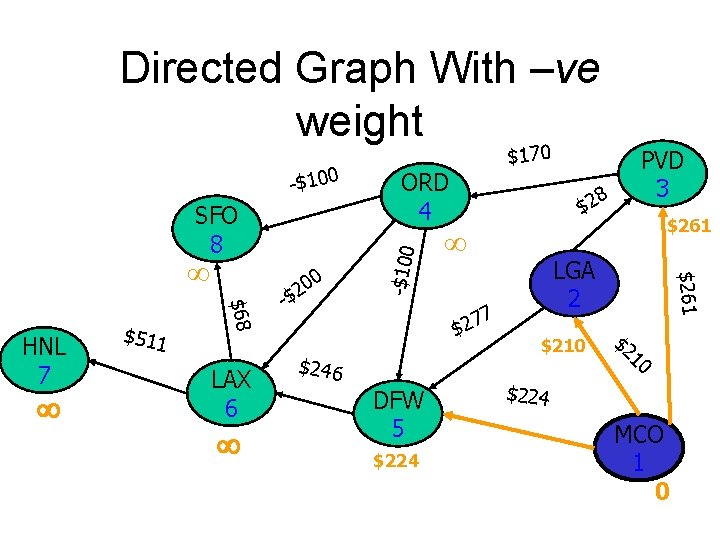
Directed Graph With –ve weight SFO 8 $511 $68 HNL 7 LAX 6 0 20 -$ 8 $2 7 7 2 $ $246 DFW 5 PVD 3 LGA 2 $261 ORD 4 -$100 $170 $2 10 $224 MCO 1 0

Directed Graph With –ve weight SFO 8 $511 $68 HNL 7 LAX 6 0 20 -$ 8 $2 7 7 2 $ $246 DFW 5 $224 PVD 3 $224 LGA 2 $210 $261 ORD 4 -$100 $170 $2 10 $224 MCO 1 0

Directed Graph With –ve weight SFO 8 $511 $68 HNL 7 LAX 6 0 20 -$ 8 $2 7 7 2 $ $246 DFW 5 $224 PVD 3 $261 LGA 2 $210 $261 ORD 4 -$100 $170 $2 10 $224 MCO 1 0

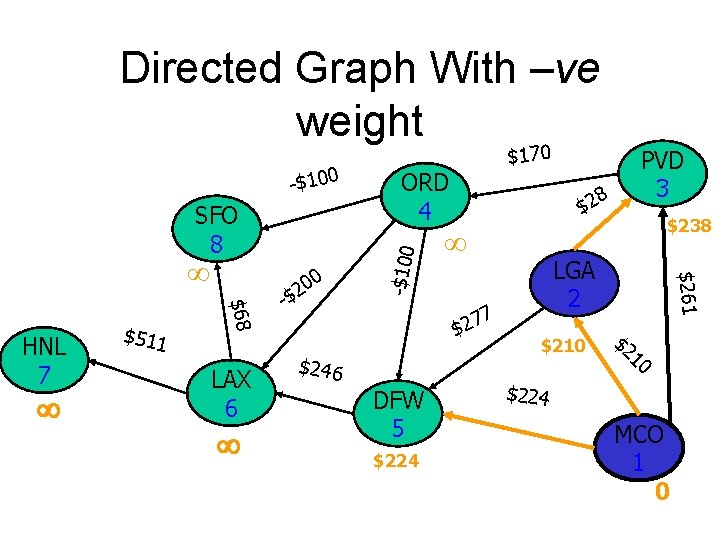
Directed Graph With –ve weight SFO 8 $511 $68 HNL 7 LAX 6 0 20 -$ 8 $2 7 7 2 $ $246 DFW 5 $224 PVD 3 $238 LGA 2 $210 $261 ORD 4 -$100 $170 $2 10 $224 MCO 1 0

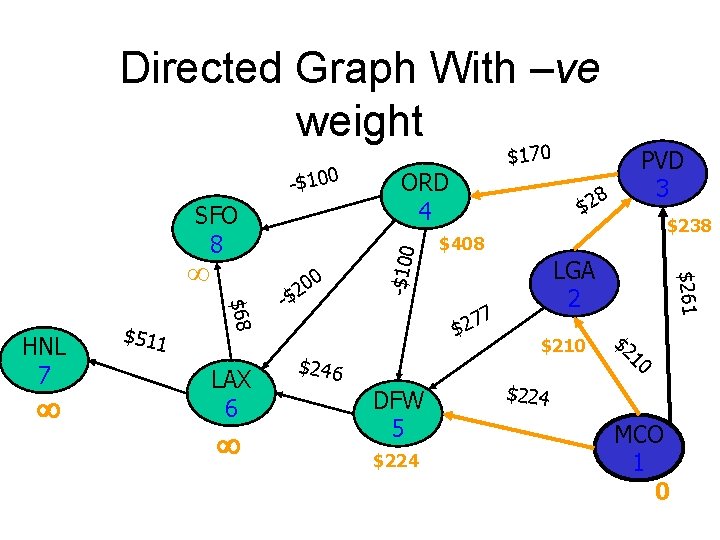
Directed Graph With –ve weight SFO 8 $511 $68 HNL 7 LAX 6 0 20 -$ 8 $2 DFW 5 $224 $238 $408 7 7 2 $ $246 PVD 3 LGA 2 $210 $261 ORD 4 -$100 $170 $2 10 $224 MCO 1 0

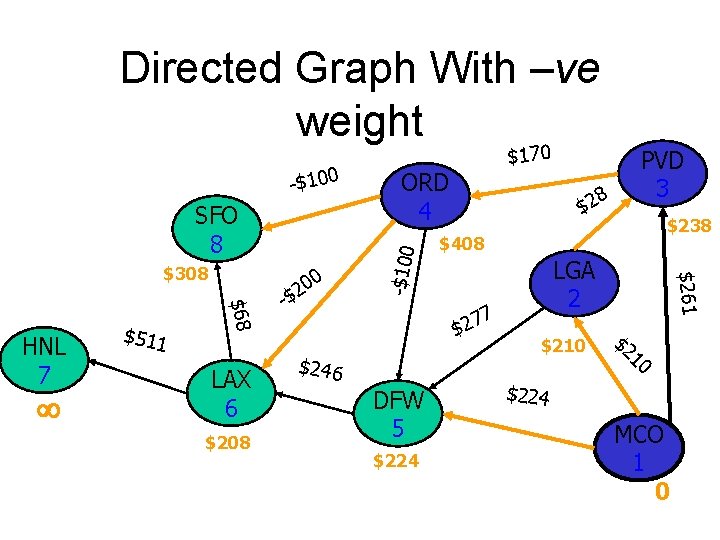
Directed Graph With –ve weight SFO 8 $511 $68 HNL 7 LAX 6 $208 0 20 -$ 8 $2 DFW 5 $224 $238 $408 7 7 2 $ $246 PVD 3 LGA 2 $210 $261 $308 ORD 4 -$100 $170 $2 10 $224 MCO 1 0

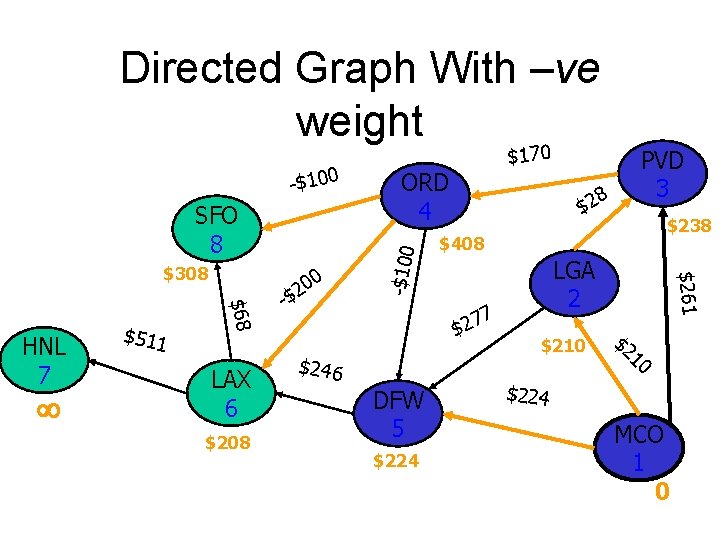
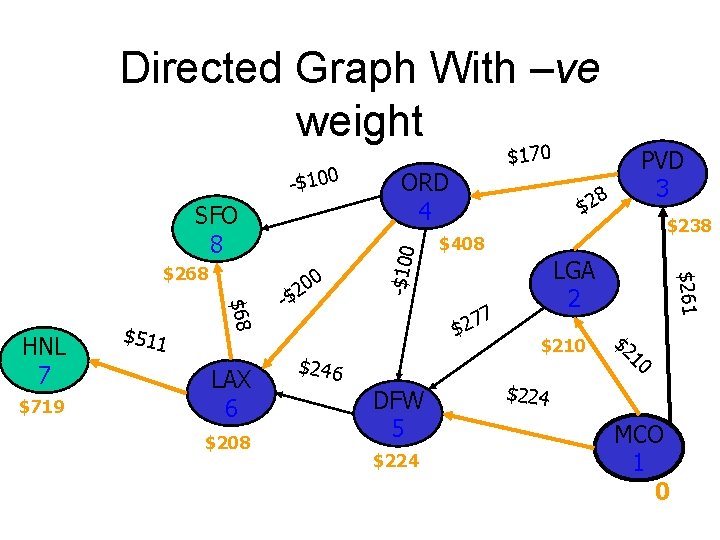
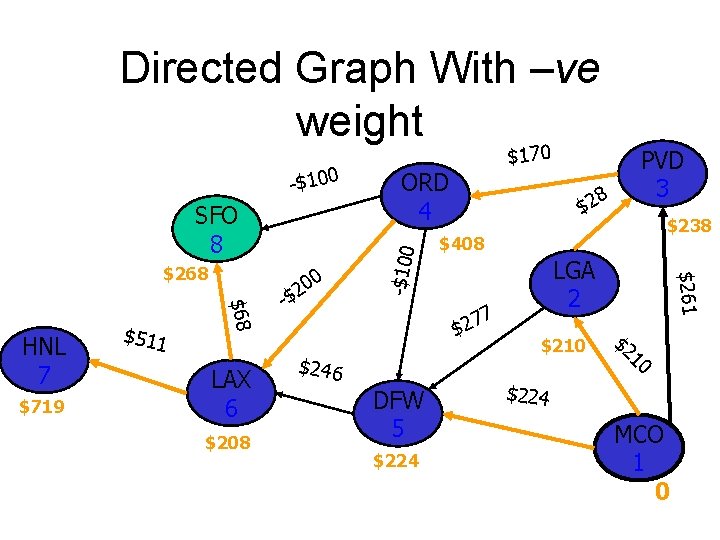
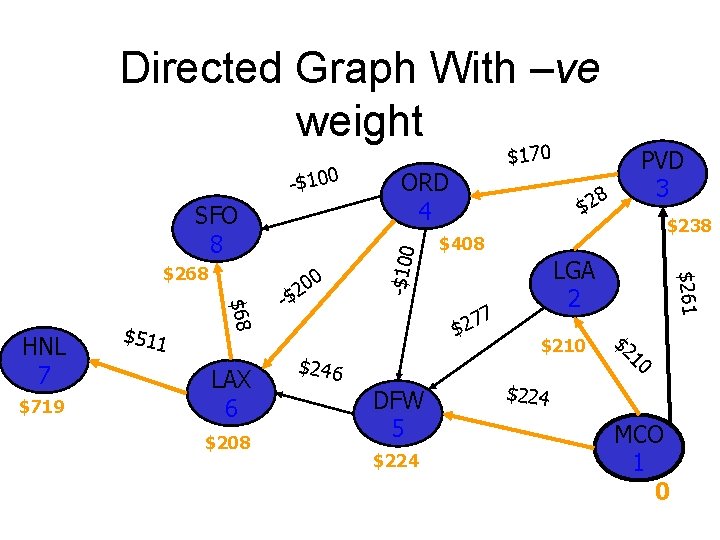
Directed Graph With –ve weight SFO 8 $719 $511 $68 HNL 7 LAX 6 $208 0 20 -$ 8 $2 DFW 5 $224 $238 $408 7 7 2 $ $246 PVD 3 LGA 2 $210 $261 $268 ORD 4 -$100 $170 $2 10 $224 MCO 1 0

DAG-based Algorithm • Works even with negative-weight edges • Uses topological order • Doesn’t use any fancy data structures • Is much faster than Dijkstra’s algorithm • Running time: O(n+m). Algorithm Dag. Distances(G, s) for all v G. vertices() v. parent null if v = s v. distance 0 else v. distance Perform a topological sort of the vertices for u 1 to n do {in topological order} for each e G. out. Edges(u) w G. opposite(u, e) r get. Distance(u) + weight(e) if r < get. Distance(w) w. distance r w. parent u