AllOptical Gyroscope Based on Sagnac Effect in Photonic

All-Optical Gyroscope Based on Sagnac Effect in Photonic Crystal Coupled Cavity Waveguides and Slow Light Structures Work published in: B. Z. Steinberg, ‘’Rotating photonic crystals: a medium for compact optical gyroscopes”, Phys. Rev. E, vol 71, pp. 056621 -7, May 31 2005

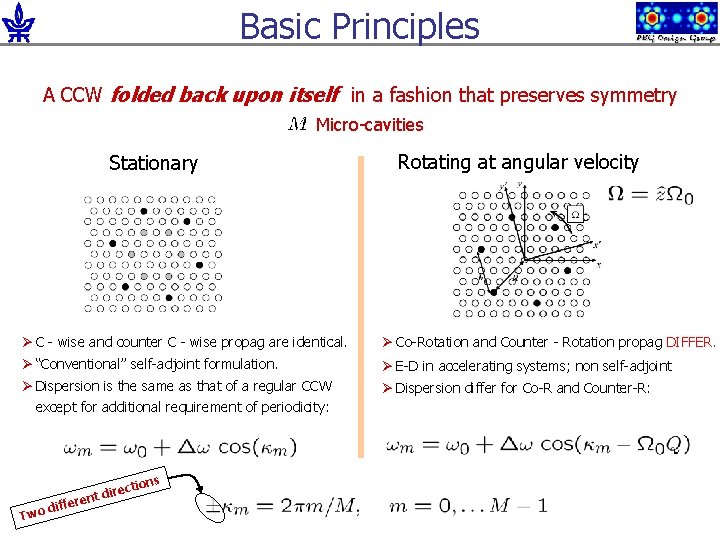
Basic Principles A CCW folded back upon itself in a fashion that preserves symmetry Micro-cavities Stationary Rotating at angular velocity Ø C - wise and counter C - wise propag are identical. Ø Co-Rotation and Counter - Rotation propag DIFFER. Ø “Conventional” self-adjoint formulation. Ø E-D in accelerating systems; non self-adjoint Ø Dispersion differ for Co-R and Counter-R: Ø Dispersion is the same as that of a regular CCW except for additional requirement of periodicity: d Two e iffer ire nt d s ction

Formulation • E-D in the rotating system frame of reference: – We have the same form of Maxwell’s equations: – But constitutive relations differ: – The resulting wave equation is (first order in velocity):

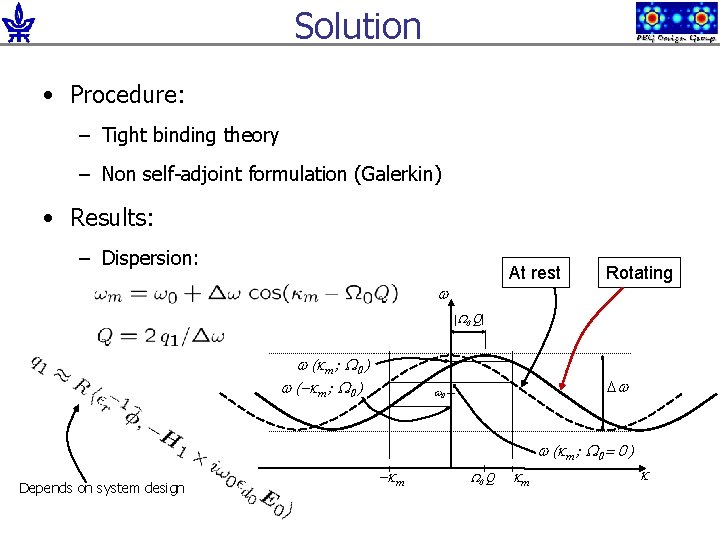
Solution • Procedure: – Tight binding theory – Non self-adjoint formulation (Galerkin) • Results: – Dispersion: At rest w Rotating |W 0 Q| w (km ; W 0 ) w (-km ; W 0 ) Dw w 0 w (km ; W 0 = 0 ) Depends on system design -km W 0 Q km k

The Gyro application • Measure beats between Co-Rot and Counter-Rot modes: • Rough estimate: • For Gyro operating at optical frequency and CCW with :